Article contents
Evolution of zero-pressure-gradient boundary layers from different tripping conditions
Published online by Cambridge University Press: 22 October 2015
Abstract
In this paper we study the spatial evolution of zero-pressure-gradient (ZPG) turbulent boundary layers from their origin to a canonical high-Reynolds-number state. A prime motivation is to better understand under what conditions reliable scaling behaviour comparisons can be made between different experimental studies at matched local Reynolds numbers. This is achieved here through detailed streamwise velocity measurements using hot wires in the large University of Melbourne wind tunnel. By keeping the unit Reynolds number constant, the flow conditioning, contraction and trip can be considered unaltered for a given boundary layer’s development and hence its evolution can be studied in isolation from the influence of inflow conditions by moving to different streamwise locations. Careful attention was given to the experimental design in order to make comparisons between flows with three different trips while keeping all other parameters nominally constant, including keeping the measurement sensor size nominally fixed in viscous wall units. The three trips consist of a standard trip and two deliberately ‘over-tripped’ cases, where the initial boundary layers are over-stimulated with additional large-scale energy. Comparisons of the mean flow, normal Reynolds stress, spectra and higher-order turbulence statistics reveal that the effects of the trip are seen to be significant, with the remnants of the ‘over-tripped’ conditions persisting at least until streamwise stations corresponding to 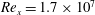 $Re_{x}=1.7\times 10^{7}$ and
$Re_{x}=1.7\times 10^{7}$ and 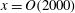 $x=O(2000)$ trip heights are reached (which is specific to the trips used here), at which position the non-canonical boundary layers exhibit a weak memory of their initial conditions at the largest scales
$x=O(2000)$ trip heights are reached (which is specific to the trips used here), at which position the non-canonical boundary layers exhibit a weak memory of their initial conditions at the largest scales 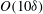 $O(10{\it\delta})$ , where
$O(10{\it\delta})$ , where 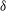 ${\it\delta}$ is the boundary layer thickness. At closer streamwise stations, no one-to-one correspondence is observed between the local Reynolds numbers (
${\it\delta}$ is the boundary layer thickness. At closer streamwise stations, no one-to-one correspondence is observed between the local Reynolds numbers ( 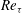 $Re_{{\it\tau}}$ ,
$Re_{{\it\tau}}$ , 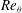 $Re_{{\it\theta}}$ or
$Re_{{\it\theta}}$ or 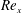 $Re_{x}$ etc.), and these differences are likely to be the cause of disparities between previous studies where a given Reynolds number is matched but without account of the trip conditions and the actual evolution of the boundary layer. In previous literature such variations have commonly been referred to as low-Reynolds-number effects, while here we show that it is more likely that these differences are due to an evolution effect resulting from the initial conditions set up by the trip and/or the initial inflow conditions. Generally, the mean velocity profiles were found to approach a constant wake parameter
$Re_{x}$ etc.), and these differences are likely to be the cause of disparities between previous studies where a given Reynolds number is matched but without account of the trip conditions and the actual evolution of the boundary layer. In previous literature such variations have commonly been referred to as low-Reynolds-number effects, while here we show that it is more likely that these differences are due to an evolution effect resulting from the initial conditions set up by the trip and/or the initial inflow conditions. Generally, the mean velocity profiles were found to approach a constant wake parameter 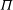 ${\it\Pi}$ as the three boundary layers developed along the test section, and agreement of the mean flow parameters was found to coincide with the location where other statistics also converged, including higher-order moments up to tenth order. This result therefore implies that it may be sufficient to document the mean flowparameters alone in order to ascertain whether the ZPG flow, as described by the streamwise velocity statistics, has reached a canonical state, and a computational approach is outlined to do this. The computational scheme is shown to agree well with available experimental data.
${\it\Pi}$ as the three boundary layers developed along the test section, and agreement of the mean flow parameters was found to coincide with the location where other statistics also converged, including higher-order moments up to tenth order. This result therefore implies that it may be sufficient to document the mean flowparameters alone in order to ascertain whether the ZPG flow, as described by the streamwise velocity statistics, has reached a canonical state, and a computational approach is outlined to do this. The computational scheme is shown to agree well with available experimental data.
JFM classification
Information
- Type
- Papers
- Information
- Copyright
- © 2015 Cambridge University Press
References
- 129
- Cited by


