Article contents
Experimental investigation of in-line flow-induced vibration of a rotating circular cylinder
Published online by Cambridge University Press: 25 May 2018
Abstract
This study experimentally investigates the in-line flow-induced vibration (FIV) of an elastically mounted circular cylinder under forced axial rotation in a free stream. The present experiments characterise the structural vibration, fluid forces and wake structure of the fluid–structure system at a low mass ratio (the ratio of the total mass to the displaced fluid mass) over a wide parameter space spanning the reduced velocity range 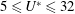 $5\leqslant U^{\ast }\leqslant 32$ and the rotation rate range
$5\leqslant U^{\ast }\leqslant 32$ and the rotation rate range 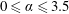 $0\leqslant \unicode[STIX]{x1D6FC}\leqslant 3.5$ , where
$0\leqslant \unicode[STIX]{x1D6FC}\leqslant 3.5$ , where 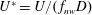 $U^{\ast }=U/(\,f_{nw}D)$ and
$U^{\ast }=U/(\,f_{nw}D)$ and 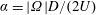 $\unicode[STIX]{x1D6FC}=|\unicode[STIX]{x1D6FA}|D/(2U)$ , with
$\unicode[STIX]{x1D6FC}=|\unicode[STIX]{x1D6FA}|D/(2U)$ , with  $U$ the free-stream velocity,
$U$ the free-stream velocity, 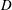 $D$ the cylinder outer diameter,
$D$ the cylinder outer diameter, 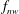 $f_{nw}$ the natural frequency of the system in quiescent water and
$f_{nw}$ the natural frequency of the system in quiescent water and  $|\unicode[STIX]{x1D6FA}|$ the angular velocity of the cylinder rotation. The corresponding Reynolds number (defined by
$|\unicode[STIX]{x1D6FA}|$ the angular velocity of the cylinder rotation. The corresponding Reynolds number (defined by 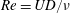 $Re=UD/\unicode[STIX]{x1D708}$ , with
$Re=UD/\unicode[STIX]{x1D708}$ , with  $\unicode[STIX]{x1D708}$ the kinematic viscosity of the fluid) was varied over the interval
$\unicode[STIX]{x1D708}$ the kinematic viscosity of the fluid) was varied over the interval 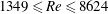 $1349\leqslant Re\leqslant 8624$ , where it is expected that the FIV response is likely to be relatively insensitive to the Reynolds number. The fluid–structure system was modelled using a low-friction air-bearing system in conjunction with a free-surface water-channel facility. Three vibration regions that exhibited vortex-induced vibration (VIV) synchronisation, rotation-induced galloping and desynchronised responses were observed. In both the VIV synchronisation and rotation-induced galloping regions, significant cylinder vibration was found to be correlated with wake–body synchronisation within the rotation rate range
$1349\leqslant Re\leqslant 8624$ , where it is expected that the FIV response is likely to be relatively insensitive to the Reynolds number. The fluid–structure system was modelled using a low-friction air-bearing system in conjunction with a free-surface water-channel facility. Three vibration regions that exhibited vortex-induced vibration (VIV) synchronisation, rotation-induced galloping and desynchronised responses were observed. In both the VIV synchronisation and rotation-induced galloping regions, significant cylinder vibration was found to be correlated with wake–body synchronisation within the rotation rate range 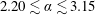 $2.20\lesssim \unicode[STIX]{x1D6FC}\lesssim 3.15$ . Of significant interest, the frequency of the streamwise fluid force could be modulated by the imposed rotation to match that of the transverse lift force, resulting in harmonic synchronisation. Measurements using the particle image velocimetry (PIV) technique were performed to identify the wake structure. Interestingly, the imposed rotation can cause regular vortex shedding in in-line FIV at rotation rates that see suppression of the Bénard–von-Kármán vortex shedding in the case of a rigidly mounted cylinder (
$2.20\lesssim \unicode[STIX]{x1D6FC}\lesssim 3.15$ . Of significant interest, the frequency of the streamwise fluid force could be modulated by the imposed rotation to match that of the transverse lift force, resulting in harmonic synchronisation. Measurements using the particle image velocimetry (PIV) technique were performed to identify the wake structure. Interestingly, the imposed rotation can cause regular vortex shedding in in-line FIV at rotation rates that see suppression of the Bénard–von-Kármán vortex shedding in the case of a rigidly mounted cylinder (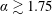 $\unicode[STIX]{x1D6FC}\gtrsim 1.75$ ). There is a monotonic increase in the drag coefficient with rotation rate beyond
$\unicode[STIX]{x1D6FC}\gtrsim 1.75$ ). There is a monotonic increase in the drag coefficient with rotation rate beyond 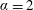 $\unicode[STIX]{x1D6FC}=2$ for a non-oscillating rotating cylinder. This suggests that the mechanism for sustaining the large rotation-induced galloping oscillations at higher
$\unicode[STIX]{x1D6FC}=2$ for a non-oscillating rotating cylinder. This suggests that the mechanism for sustaining the large rotation-induced galloping oscillations at higher  $\unicode[STIX]{x1D6FC}$ is due to a combination of aerodynamic forcing from the locked induced vortex shedding associated with the oscillations, assisted by aerodynamic forcing, evaluated using quasi-steady theory.
$\unicode[STIX]{x1D6FC}$ is due to a combination of aerodynamic forcing from the locked induced vortex shedding associated with the oscillations, assisted by aerodynamic forcing, evaluated using quasi-steady theory.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
Zhao et al. supplementary movie 5
Phase-averaged vorticity contours showing evolution of the A(2S) wake pattern at (α, U*) = (2.75, 10.0).
- 44
- Cited by


