1 Introduction
Faraday waves and droplet impact have been separate research areas for much of the last century. Although Walker (Reference Walker1978) showed that a droplet may ‘float’ on a vertically vibrating bath of fluid, it was not until the last decade that this connection was re-explored. In 2005, Couder and co-workers showed that for sufficiently large, yet subcritical, vibrations of the liquid bath, a droplet may bounce periodically on the surface (Couder et al. Reference Couder, Protière, Fort and Boudaoud2005b ). At each impact, a capillary wave propagates away from the droplet, exciting a field of standing Faraday waves in its wake. For larger forcing, the bouncing destabilises, and the droplet ‘walks’ across the surface of the bath, propelled at each impact by the slope of its associated wave field. As the forcing vibration increases, so does the decay time of the Faraday waves. This yields a path ‘memory’ from previous droplet impacts (Eddi et al. Reference Eddi, Sultan, Moukhtar, Fort, Rossi and Couder2011), leading to a macroscopic particle–wave interaction, as previously envisaged as an explanation for quantum behaviour (de Broglie Reference de Broglie1926). This analogy has since been explored through a remarkable series of experiments, summarised in detail by Bush (Reference Bush2015).
Several quantum analogies have been pursued. A walking droplet passing through a slit between submerged walls yielded the diffraction and interference patterns for single- and double-slit experiments respectively (Couder & Fort Reference Couder and Fort2006, Reference Couder and Fort2011). This effect was due to the interaction of the wave field with the walls. Furthermore, a droplet may ‘tunnel’ across the submerged wall separating two deep regions; as the wall width increases, the tunnelling probability decreases (Eddi et al. Reference Eddi, Fort, Moisy and Couder2009). Moreover, Harris et al. (Reference Harris, Moukhtar, Fort, Couder and Bush2013) found that the position of a chaotic walker in a circular corral exhibits wave-like statistics, whose maxima correspond to the zeros of the fundamental Faraday mode. This is reminiscent of an electron in a quantum corral.
The interaction between droplets also yields quantum analogues, such as fixed lattices of bouncing droplets and bound states (Protière, Boudaoud & Couder Reference Protière, Boudaoud and Couder2006; Eddi et al. Reference Eddi, Terwagne, Fort and Couder2008). At the approach of two walking droplets, the interaction between wave fields leads to either scatter or locking in circular orbital motion with quantised orbit diameters (Couder et al. Reference Couder, Protière, Fort and Boudaoud2005b ). For droplets of different sizes, one droplet may orbit the other, with complex epicycles emerging (Protière, Bohn & Couder Reference Protière, Bohn and Couder2008). Two droplets walking in parallel interact through the wave field, and stable transverse oscillations ensue (Protière et al. Reference Protière, Boudaoud and Couder2006); these ‘promenade’ modes have been observed to have quantised average distances between the droplets (Borghesi et al. Reference Borghesi, Moukhtar, Labousse, Eddi, Fort and Couder2014).
Further analogues occur when a droplet walks on a rotating bath. Due to the Coriolis force, the droplet moves in a circular motion in the rotating frame (Fort et al. Reference Fort, Eddi, Boudaoud, Moukhtar and Couder2010). As the forcing vibration is increased, the wave field forces the orbit diameters to be quantised, with a macroscopic analogy to Landau levels (Oza et al. Reference Oza, Harris, Rosales and Bush2014a ). In the long-memory limit, more exotic trajectories occur, including drifting, wobbling and quasi-periodic orbits (Oza et al. Reference Oza, Wind-Willassen, Harris, Rosales and Bush2014b ). In particular, the stationary probability distribution for the droplet position exhibits wave-like statistics, with maxima at its unstable steady states (Harris & Bush Reference Harris and Bush2014). Two droplets may orbit each other in the rotating frame, but their orbit diameters exhibit Zeeman-like splitting depending on whether the orbits are co-/anti-rotational relative to the bath (Eddi et al. Reference Eddi, Moukhtar, Perrard, Fort and Couder2012).
Circular orbits also exist for a droplet in a harmonic potential (Perrard et al. Reference Perrard, Labousse, Miskin, Fort and Couder2014b ), with their convergence explored by Labousse & Perrard (Reference Labousse and Perrard2014). At long memory, the orbit diameters are quantised (Labousse et al. Reference Labousse, Oza, Perrard and Bush2016), and an array of stable exotic trajectories forms, with a double quantisation in their average radius and angular momentum (Perrard et al. Reference Perrard, Labousse, Miskin, Fort and Couder2014b ). The underlying pivot structure of the wave field governing these trajectories has been explored by Labousse et al. (Reference Labousse, Perrard, Couder and Fort2014). In the chaotic regime, the switching time between trajectories is probabilistic (Perrard et al. Reference Perrard, Labousse, Fort and Couder2014a ).
The above dynamics are governed by a complex set of physical phenomena. For a bath vibrated sinusoidally with amplitude
![]() $A$
and frequency
$A$
and frequency
![]() $\unicode[STIX]{x1D714}_{0}/(2\unicode[STIX]{x03C0})$
, the stability of the Faraday waves is governed by
$\unicode[STIX]{x1D714}_{0}/(2\unicode[STIX]{x03C0})$
, the stability of the Faraday waves is governed by
![]() $\unicode[STIX]{x1D6E4}=A\unicode[STIX]{x1D714}_{0}^{2}/g$
, which is the ratio of peak forcing acceleration relative to gravity. In both the inviscid (Benjamin & Ursell Reference Benjamin and Ursell1954) and viscous (Kumar & Tuckerman Reference Kumar and Tuckerman1994; Kumar Reference Kumar1996) cases, a spectral decomposition yields a system of Mathieu equations, whose stability depends on
$\unicode[STIX]{x1D6E4}=A\unicode[STIX]{x1D714}_{0}^{2}/g$
, which is the ratio of peak forcing acceleration relative to gravity. In both the inviscid (Benjamin & Ursell Reference Benjamin and Ursell1954) and viscous (Kumar & Tuckerman Reference Kumar and Tuckerman1994; Kumar Reference Kumar1996) cases, a spectral decomposition yields a system of Mathieu equations, whose stability depends on
![]() $\unicode[STIX]{x1D6E4}>0$
. In the dissipative case, the surface destabilises at
$\unicode[STIX]{x1D6E4}>0$
. In the dissipative case, the surface destabilises at
![]() $\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E4}_{F}$
(the Faraday threshold), which corresponds to the critical wavenumber
$\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E4}_{F}$
(the Faraday threshold), which corresponds to the critical wavenumber
![]() $k=k_{F}$
and subharmonic waves (relative to the forcing frequency).
$k=k_{F}$
and subharmonic waves (relative to the forcing frequency).
In all non-coalescing states, the droplet and bath remain separated by a thin air lubrication layer (Walker Reference Walker1978), where the air slowly escapes (Couder et al.
Reference Couder, Fort, Gautier and Boudaoud2005a
). The restoring forces of the wave field transmitted through the lubrication layer propel the droplet back into the air before coalescence, leading to periodic bouncing. The bouncing threshold
![]() $\unicode[STIX]{x1D6E4}_{B}$
has been investigated through lubrication theory (Gilet et al.
Reference Gilet, Terwagne, Vandewalle and Dorbolo2008) and a spring model for droplet impact (Hubert et al.
Reference Hubert, Robert, Caps, Dorbolo and Vandewalle2015).
$\unicode[STIX]{x1D6E4}_{B}$
has been investigated through lubrication theory (Gilet et al.
Reference Gilet, Terwagne, Vandewalle and Dorbolo2008) and a spring model for droplet impact (Hubert et al.
Reference Hubert, Robert, Caps, Dorbolo and Vandewalle2015).
For
![]() $\unicode[STIX]{x1D6E4}>\unicode[STIX]{x1D6E4}_{B}$
, a range of bouncing dynamics occur, which destabilise to walking at
$\unicode[STIX]{x1D6E4}>\unicode[STIX]{x1D6E4}_{B}$
, a range of bouncing dynamics occur, which destabilise to walking at
![]() $\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E4}_{W}>\unicode[STIX]{x1D6E4}_{B}$
. The vertical dynamics of walkers are frequently observed to be in subharmonic resonance with the wave field, although a range of periodic and chaotic dynamics exist. Following Gilet & Bush (Reference Gilet and Bush2009), we distinguish different vertical dynamics by
$\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E4}_{W}>\unicode[STIX]{x1D6E4}_{B}$
. The vertical dynamics of walkers are frequently observed to be in subharmonic resonance with the wave field, although a range of periodic and chaotic dynamics exist. Following Gilet & Bush (Reference Gilet and Bush2009), we distinguish different vertical dynamics by
![]() $(m,n)$
, where
$(m,n)$
, where
![]() $m$
is the number of forcing periods and
$m$
is the number of forcing periods and
![]() $n$
is the number of impacts for the dynamics to repeat. The aforementioned subharmonic
$n$
is the number of impacts for the dynamics to repeat. The aforementioned subharmonic
![]() $(2,1)$
mode has two distinct energy levels: the lower-energy
$(2,1)$
mode has two distinct energy levels: the lower-energy
![]() $(2,1)^{1}$
mode and the higher-energy
$(2,1)^{1}$
mode and the higher-energy
![]() $(2,1)^{2}$
mode observed at higher
$(2,1)^{2}$
mode observed at higher
![]() $\unicode[STIX]{x1D6E4}$
, where the impact durations are much shorter. The bifurcation to different
$\unicode[STIX]{x1D6E4}$
, where the impact durations are much shorter. The bifurcation to different
![]() $(m,n)$
regimes as a function of droplet diameter and
$(m,n)$
regimes as a function of droplet diameter and
![]() $\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6E4}_{F}$
was recorded by Protière et al. (Reference Protière, Boudaoud and Couder2006) and Eddi et al. (Reference Eddi, Terwagne, Fort and Couder2008). However, Moláček & Bush (Reference Moláček and Bush2013a
) showed that the bouncing thresholds for different fluids collapse onto a single curve if the drops are instead characterised by their dimensionless vibration number,
$\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6E4}_{F}$
was recorded by Protière et al. (Reference Protière, Boudaoud and Couder2006) and Eddi et al. (Reference Eddi, Terwagne, Fort and Couder2008). However, Moláček & Bush (Reference Moláček and Bush2013a
) showed that the bouncing thresholds for different fluids collapse onto a single curve if the drops are instead characterised by their dimensionless vibration number,
where
![]() $R_{0}$
is the droplet radius, with fluid density
$R_{0}$
is the droplet radius, with fluid density
![]() $\unicode[STIX]{x1D70C}$
and surface tension
$\unicode[STIX]{x1D70C}$
and surface tension
![]() $\unicode[STIX]{x1D70E}$
. This is the frequency ratio of bath vibrations to characteristic droplet oscillations. Regime diagrams in the
$\unicode[STIX]{x1D70E}$
. This is the frequency ratio of bath vibrations to characteristic droplet oscillations. Regime diagrams in the
![]() $(\unicode[STIX]{x1D6E4},\unicode[STIX]{x1D6FA})$
-plane are found in Wind-Willassen et al. (Reference Wind-Willassen, Moláček, Harris and Bush2013).
$(\unicode[STIX]{x1D6E4},\unicode[STIX]{x1D6FA})$
-plane are found in Wind-Willassen et al. (Reference Wind-Willassen, Moláček, Harris and Bush2013).
Due to the complexity of this system, no unified model exists to describe all of the observed dynamics. The first simple model captured the qualitative bifurcation from bouncing to walking through a period-averaged differential equation for the droplet position, but this was valid only in the low-memory limit and the
![]() $(2,1)$
mode (Couder et al.
Reference Couder, Protière, Fort and Boudaoud2005b
; Protière et al.
Reference Protière, Boudaoud and Couder2006).
$(2,1)$
mode (Couder et al.
Reference Couder, Protière, Fort and Boudaoud2005b
; Protière et al.
Reference Protière, Boudaoud and Couder2006).
Assuming a linear wave field, Fort et al. (Reference Fort, Eddi, Boudaoud, Moukhtar and Couder2010) modelled the wave field as a superposition of exponentially decaying (in time) standing waves centred at each (instantaneous) impact, with the droplet dynamics restricted to the predominant
![]() $(2,1)$
mode. The wave field generated at each impact was the far-field approximation to the Bessel function
$(2,1)$
mode. The wave field generated at each impact was the far-field approximation to the Bessel function
![]() $\text{J}_{0}(k_{F}r)$
with an experimentally observed exponential spatial decay correction. Although this model numerically verified the quantised orbits in a rotating bath, it was not analysed mathematically, not least due to the spatial singularity centred at each droplet impact.
$\text{J}_{0}(k_{F}r)$
with an experimentally observed exponential spatial decay correction. Although this model numerically verified the quantised orbits in a rotating bath, it was not analysed mathematically, not least due to the spatial singularity centred at each droplet impact.
With no spatial damping correction, Moláček & Bush (Reference Moláček and Bush2013b
) coupled the wave dynamics with a logarithmic spring model for the vertical motion of the droplet (Moláček & Bush Reference Moláček and Bush2013a
). This model successfully predicts many of the experimentally observed bouncing and walking
![]() $(m,n)$
modes (Wind-Willassen et al.
Reference Wind-Willassen, Moláček, Harris and Bush2013), but relies on experimentally fitted parameters and is too complex for mathematical analysis.
$(m,n)$
modes (Wind-Willassen et al.
Reference Wind-Willassen, Moláček, Harris and Bush2013), but relies on experimentally fitted parameters and is too complex for mathematical analysis.
To simplify this, Oza, Rosales & Bush (Reference Oza, Rosales and Bush2013) observed that the time scale of the horizontal motion is much greater than that of the vertical motion in the
![]() $(2,1)$
mode. Under this assumption, they approximated the sum of instantaneous impacts by a continuous integral, leading to an integro-differential trajectory equation for the droplet, which records the entire path history of the droplet (unlike the low-memory limit model of Protière et al. (Reference Protière, Boudaoud and Couder2006)). This past behaviour can be approximated in the small-acceleration limit, yielding a hydrodynamic boost factor for the droplet mass from its wave field interaction (Bush, Oza & Moláček Reference Bush, Oza and Moláček2014). By studying the trajectory equation, analytic expressions are obtained for the bifurcation from bouncing to walking and the walking speed (Oza et al.
Reference Oza, Rosales and Bush2013), circular orbits in a rotating frame (Oza et al.
Reference Oza, Harris, Rosales and Bush2014a
) and circular orbits in a harmonic potential (Labousse et al.
Reference Labousse, Oza, Perrard and Bush2016). Advantageously, the linear stability of these dynamics can be obtained analytically from the trajectory equation.
$(2,1)$
mode. Under this assumption, they approximated the sum of instantaneous impacts by a continuous integral, leading to an integro-differential trajectory equation for the droplet, which records the entire path history of the droplet (unlike the low-memory limit model of Protière et al. (Reference Protière, Boudaoud and Couder2006)). This past behaviour can be approximated in the small-acceleration limit, yielding a hydrodynamic boost factor for the droplet mass from its wave field interaction (Bush, Oza & Moláček Reference Bush, Oza and Moláček2014). By studying the trajectory equation, analytic expressions are obtained for the bifurcation from bouncing to walking and the walking speed (Oza et al.
Reference Oza, Rosales and Bush2013), circular orbits in a rotating frame (Oza et al.
Reference Oza, Harris, Rosales and Bush2014a
) and circular orbits in a harmonic potential (Labousse et al.
Reference Labousse, Oza, Perrard and Bush2016). Advantageously, the linear stability of these dynamics can be obtained analytically from the trajectory equation.
The above models all have one fundamental shortcoming: they simplify the complex wave field generated by each droplet impact by decoupling the radial and temporal behaviour. To remedy this, Eddi et al. (Reference Eddi, Sultan, Moukhtar, Fort, Rossi and Couder2011) modelled the wave field depression around the droplet during impact as a finite cap, which evolves under the wave dynamics of Benjamin & Ursell (Reference Benjamin and Ursell1954) with a phenomenological viscous damping factor. As this model includes a range of wavenumbers (rather than just
![]() $k_{F}$
), the experimentally observed spatial damping is automatically captured. As an alternative to computing the dynamics of many wavenumbers, Moláček & Bush (Reference Moláček and Bush2013b
) (non-rigorously) suggested that the single impact is
$k_{F}$
), the experimentally observed spatial damping is automatically captured. As an alternative to computing the dynamics of many wavenumbers, Moláček & Bush (Reference Moláček and Bush2013b
) (non-rigorously) suggested that the single impact is
![]() $\text{J}_{0}(k_{F}r)$
, spatially corrected by a radial Gaussian with a linear temporal decay length, and exponentially decaying in time. On superposition, the exponential spatial decay correction for the wave field of a bouncer is recovered (Damiano et al.
Reference Damiano, Brun, Harris, Galeano-Rios and Bush2016).
$\text{J}_{0}(k_{F}r)$
, spatially corrected by a radial Gaussian with a linear temporal decay length, and exponentially decaying in time. On superposition, the exponential spatial decay correction for the wave field of a bouncer is recovered (Damiano et al.
Reference Damiano, Brun, Harris, Galeano-Rios and Bush2016).
The approximations in the aforementioned models prevent their usage in two important situations: complex vertical droplet dynamics (without the restriction to the
![]() $(2,1)$
mode) and the effect of submerged topography. By adopting the theory of quasi-potential flow (Dias, Dyachenko & Zakharov Reference Dias, Dyachenko and Zakharov2008), coupled with the logarithmic spring model for the vertical dynamics of the droplet (Moláček & Bush Reference Moláček and Bush2013a
), Milewski et al. (Reference Milewski, Galeano-Rios, Nachbin and Bush2015) accurately predicted the bifurcations between different bouncing and walking modes, and the observed exponential spatial damping, and, in principle, the model may be adapted for any geometry.
$(2,1)$
mode) and the effect of submerged topography. By adopting the theory of quasi-potential flow (Dias, Dyachenko & Zakharov Reference Dias, Dyachenko and Zakharov2008), coupled with the logarithmic spring model for the vertical dynamics of the droplet (Moláček & Bush Reference Moláček and Bush2013a
), Milewski et al. (Reference Milewski, Galeano-Rios, Nachbin and Bush2015) accurately predicted the bifurcations between different bouncing and walking modes, and the observed exponential spatial damping, and, in principle, the model may be adapted for any geometry.
The model presented herein considers the accurate wave field model of Milewski et al. (Reference Milewski, Galeano-Rios, Nachbin and Bush2015) together with the simplifications of instantaneous and point impacts. In a sense, this is the opposite limit to the trajectory equation of Oza et al. (Reference Oza, Rosales and Bush2013). In § 2, we present the wave field equations of Milewski et al. (Reference Milewski, Galeano-Rios, Nachbin and Bush2015) and droplet dynamics of Moláček & Bush (Reference Moláček and Bush2013b ). In § 3, we perform a basis function expansion to collapse the model to a system of Mathieu differential equations. Assuming instantaneous impacts, the wave and droplet dynamics are only computed at discrete times, and the full problem collapses to a discrete map, yielding efficient computation of the dynamics and definitive stability results for various states. We capture bouncing (§ 4) and walking states, and the bifurcation between them (§ 5). We explore the quantisations of orbiting and promenading pairs, with the first investigation of walking droplet trains (§ 6). Finally, we model circular orbits of a droplet in a harmonic potential and capture the double quantisation of Perrard et al. (Reference Perrard, Labousse, Miskin, Fort and Couder2014b ) via statistical methods in the chaotic regime (§ 7).
2 Model derivation
2.1 Wave dynamics
We employ the governing equations derived by Milewski et al. (Reference Milewski, Galeano-Rios, Nachbin and Bush2015), who considered an incompressible viscous fluid in an infinite domain, with a small vortical boundary layer at the surface. Since a bouncing droplet emits radially symmetric waves, it is natural to write the spatial system in cylindrical polar coordinates
![]() $(r,\unicode[STIX]{x1D703},z)$
. Assuming that the waves and fluid velocity are small with a shallow wave slope, the velocity potential
$(r,\unicode[STIX]{x1D703},z)$
. Assuming that the waves and fluid velocity are small with a shallow wave slope, the velocity potential
![]() $\unicode[STIX]{x1D719}(r,\unicode[STIX]{x1D703},z,t)$
and wave perturbation
$\unicode[STIX]{x1D719}(r,\unicode[STIX]{x1D703},z,t)$
and wave perturbation
![]() $\unicode[STIX]{x1D702}(r,\unicode[STIX]{x1D703},t)$
at time
$\unicode[STIX]{x1D702}(r,\unicode[STIX]{x1D703},t)$
at time
![]() $t>0$
satisfy the linearised system
$t>0$
satisfy the linearised system
with
![]() $\unicode[STIX]{x1D735}\unicode[STIX]{x1D719}\rightarrow \mathbf{0}$
and
$\unicode[STIX]{x1D735}\unicode[STIX]{x1D719}\rightarrow \mathbf{0}$
and
![]() $\unicode[STIX]{x1D702}\rightarrow 0$
in the far field. In the above, we have constant surface tension
$\unicode[STIX]{x1D702}\rightarrow 0$
in the far field. In the above, we have constant surface tension
![]() $\unicode[STIX]{x1D70E}$
, density
$\unicode[STIX]{x1D70E}$
, density
![]() $\unicode[STIX]{x1D70C}$
and kinematic viscosity
$\unicode[STIX]{x1D70C}$
and kinematic viscosity
![]() $\unicode[STIX]{x1D708}$
, where
$\unicode[STIX]{x1D708}$
, where
![]() $\unicode[STIX]{x1D6FB}_{H}^{2}$
is the horizontal Laplacian.
$\unicode[STIX]{x1D6FB}_{H}^{2}$
is the horizontal Laplacian.
In the vibrating frame, the effective gravity is
![]() $g_{\unicode[STIX]{x1D6E4}}(t)\equiv g(1-\unicode[STIX]{x1D6E4}\cos (\unicode[STIX]{x1D714}_{0}t))$
, where
$g_{\unicode[STIX]{x1D6E4}}(t)\equiv g(1-\unicode[STIX]{x1D6E4}\cos (\unicode[STIX]{x1D714}_{0}t))$
, where
![]() $\unicode[STIX]{x1D714}_{0}/(2\unicode[STIX]{x03C0})$
is the vibration frequency and
$\unicode[STIX]{x1D714}_{0}/(2\unicode[STIX]{x03C0})$
is the vibration frequency and
![]() $\unicode[STIX]{x1D6E4}$
is the ratio of maximum vibration acceleration relative to gravity
$\unicode[STIX]{x1D6E4}$
is the ratio of maximum vibration acceleration relative to gravity
![]() $g$
. As the droplet impacts the surface, the externally applied pressure on the bath is given by
$g$
. As the droplet impacts the surface, the externally applied pressure on the bath is given by
![]() $P(r,\unicode[STIX]{x1D703},t)$
, which we prescribe in § 3. Coupled with droplet dynamics, Milewski et al. (Reference Milewski, Galeano-Rios, Nachbin and Bush2015) solved this system numerically, but we make several simplifying assumptions to analyse a wide range of dynamics observed in an unbounded domain.
$P(r,\unicode[STIX]{x1D703},t)$
, which we prescribe in § 3. Coupled with droplet dynamics, Milewski et al. (Reference Milewski, Galeano-Rios, Nachbin and Bush2015) solved this system numerically, but we make several simplifying assumptions to analyse a wide range of dynamics observed in an unbounded domain.
2.2 Droplet dynamics
By adapting the work of Moláček & Bush (Reference Moláček and Bush2013b
), we model the droplet dynamics as a rigid sphere of mass
![]() $m$
under ballistic motion centred at the point
$m$
under ballistic motion centred at the point
![]() $(\boldsymbol{x},z)=(\boldsymbol{X}(t),Z(t))$
in Cartesian coordinates. This neglects droplet deformation, which is a reasonable assumption for the small droplets considered (Moláček & Bush Reference Moláček and Bush2013b
). During flight, the droplet experiences an aerodynamical force described by Stokes drag, namely
$(\boldsymbol{x},z)=(\boldsymbol{X}(t),Z(t))$
in Cartesian coordinates. This neglects droplet deformation, which is a reasonable assumption for the small droplets considered (Moláček & Bush Reference Moláček and Bush2013b
). During flight, the droplet experiences an aerodynamical force described by Stokes drag, namely
![]() $-\unicode[STIX]{x1D708}_{p}\boldsymbol{X}^{\prime }(t)$
and
$-\unicode[STIX]{x1D708}_{p}\boldsymbol{X}^{\prime }(t)$
and
![]() $-\unicode[STIX]{x1D708}_{p}Z^{\prime }(t)$
in the horizontal and vertical directions respectively. Here,
$-\unicode[STIX]{x1D708}_{p}Z^{\prime }(t)$
in the horizontal and vertical directions respectively. Here,
![]() $\unicode[STIX]{x1D708}_{p}=6\unicode[STIX]{x03C0}R_{0}\unicode[STIX]{x1D707}_{air}$
for droplet radius
$\unicode[STIX]{x1D708}_{p}=6\unicode[STIX]{x03C0}R_{0}\unicode[STIX]{x1D707}_{air}$
for droplet radius
![]() $R_{0}$
and air viscosity
$R_{0}$
and air viscosity
![]() $\unicode[STIX]{x1D707}_{air}$
(Moláček & Bush Reference Moláček and Bush2013b
).
$\unicode[STIX]{x1D707}_{air}$
(Moláček & Bush Reference Moláček and Bush2013b
).
The droplet experiences a force of magnitude
![]() $f(t)\geqslant 0$
due to the lubrication air layer during impact (
$f(t)\geqslant 0$
due to the lubrication air layer during impact (
![]() $f=0$
during flight). As the droplet radius
$f=0$
during flight). As the droplet radius
![]() $R_{0}$
is much smaller than a typical wavelength
$R_{0}$
is much smaller than a typical wavelength
![]() $\unicode[STIX]{x1D706}$
(
$\unicode[STIX]{x1D706}$
(
![]() $R_{0}/\unicode[STIX]{x1D706}\ll 1$
), the forces experienced from the wave field interaction are localised to the point
$R_{0}/\unicode[STIX]{x1D706}\ll 1$
), the forces experienced from the wave field interaction are localised to the point
![]() $\boldsymbol{x}=\boldsymbol{X}(t)$
on the fluid surface. These are modelled as an impulsive force
$\boldsymbol{x}=\boldsymbol{X}(t)$
on the fluid surface. These are modelled as an impulsive force
![]() $f(t)\hat{\boldsymbol{n}}(\boldsymbol{X}(t),t)$
and shear forces described by the skidding friction
$f(t)\hat{\boldsymbol{n}}(\boldsymbol{X}(t),t)$
and shear forces described by the skidding friction
![]() $-c\sqrt{\unicode[STIX]{x1D70C}R_{0}/\unicode[STIX]{x1D70E}}f(t)\boldsymbol{X}^{\prime }(t)$
. Here,
$-c\sqrt{\unicode[STIX]{x1D70C}R_{0}/\unicode[STIX]{x1D70E}}f(t)\boldsymbol{X}^{\prime }(t)$
. Here,
![]() $\hat{\boldsymbol{n}}=(-\unicode[STIX]{x1D735}\unicode[STIX]{x1D702},1)/(1+|\unicode[STIX]{x1D735}\unicode[STIX]{x1D702}|^{2})^{-1/2}$
is the unit normal away from the fluid surface and
$\hat{\boldsymbol{n}}=(-\unicode[STIX]{x1D735}\unicode[STIX]{x1D702},1)/(1+|\unicode[STIX]{x1D735}\unicode[STIX]{x1D702}|^{2})^{-1/2}$
is the unit normal away from the fluid surface and
![]() $c$
is the dimensionless skidding friction coefficient introduced by Moláček & Bush (Reference Moláček and Bush2013b
) (this is discussed in § 3.3). As the fluid model assumes a shallow wave slope
$c$
is the dimensionless skidding friction coefficient introduced by Moláček & Bush (Reference Moláček and Bush2013b
) (this is discussed in § 3.3). As the fluid model assumes a shallow wave slope
![]() $|\unicode[STIX]{x1D735}\unicode[STIX]{x1D702}|\ll 1$
, we approximate
$|\unicode[STIX]{x1D735}\unicode[STIX]{x1D702}|\ll 1$
, we approximate
![]() $\hat{\boldsymbol{n}}\sim (-\unicode[STIX]{x1D735}\unicode[STIX]{x1D702},1)$
.
$\hat{\boldsymbol{n}}\sim (-\unicode[STIX]{x1D735}\unicode[STIX]{x1D702},1)$
.
For analogies to quantum mechanics, experiments are construed to subject the horizontal motion of the droplet to an external potential
![]() ${\mathcal{V}}(\boldsymbol{X}(t),t)$
, such as the dynamics in a rotating bath (Fort et al.
Reference Fort, Eddi, Boudaoud, Moukhtar and Couder2010) and a horizontal harmonic potential well (Perrard et al.
Reference Perrard, Labousse, Miskin, Fort and Couder2014b
). On combining these forces, conservation of momentum supplies
${\mathcal{V}}(\boldsymbol{X}(t),t)$
, such as the dynamics in a rotating bath (Fort et al.
Reference Fort, Eddi, Boudaoud, Moukhtar and Couder2010) and a horizontal harmonic potential well (Perrard et al.
Reference Perrard, Labousse, Miskin, Fort and Couder2014b
). On combining these forces, conservation of momentum supplies
written in the vibrating frame. In what follows, we take
![]() ${\mathcal{V}}\equiv 0$
for free walking dynamics, or
${\mathcal{V}}\equiv 0$
for free walking dynamics, or
![]() ${\mathcal{V}}=(1/2)\unicode[STIX]{x1D705}|\boldsymbol{X}(t)|^{2}$
for dynamics in a harmonic potential well with an adjustable spring constant
${\mathcal{V}}=(1/2)\unicode[STIX]{x1D705}|\boldsymbol{X}(t)|^{2}$
for dynamics in a harmonic potential well with an adjustable spring constant
![]() $\unicode[STIX]{x1D705}\geqslant 0$
. The analysis for other potentials follows akin to this work.
$\unicode[STIX]{x1D705}\geqslant 0$
. The analysis for other potentials follows akin to this work.
For simplicity, we assume that the bouncing droplet lies in the prevalent
![]() $(2,1)$
mode, which implies that both
$(2,1)$
mode, which implies that both
![]() $Z(t)$
and
$Z(t)$
and
![]() $f(t)$
are periodic with subharmonic period
$f(t)$
are periodic with subharmonic period
![]() $T=4\unicode[STIX]{x03C0}/\unicode[STIX]{x1D714}_{0}$
. By integrating (2.5) over an impact period and exploiting periodicity,
$T=4\unicode[STIX]{x03C0}/\unicode[STIX]{x1D714}_{0}$
. By integrating (2.5) over an impact period and exploiting periodicity,
![]() $f(t)$
must satisfy
$f(t)$
must satisfy
as derived by Moláček & Bush (Reference Moláček and Bush2013b
). Although we could carefully model the force
![]() $f(t)$
as a response to the impact dynamics (e.g. as a logarithmic spring (Moláček & Bush Reference Moláček and Bush2013a
)), we use condition (2.6) to prescribe a reasonable choice of
$f(t)$
as a response to the impact dynamics (e.g. as a logarithmic spring (Moláček & Bush Reference Moláček and Bush2013a
)), we use condition (2.6) to prescribe a reasonable choice of
![]() $f(t)$
in § 3.2.
$f(t)$
in § 3.2.
Table 1. Fixed variables used in this model.

3 Model reduction
For mathematical analysis, we non-dimensionalise the governing equations (2.1)–(2.4) and condition (2.6). We rescale the lengths to a typical wavelength
![]() $\unicode[STIX]{x1D706}=0.51$
cm and time to the subharmonic bouncing period
$\unicode[STIX]{x1D706}=0.51$
cm and time to the subharmonic bouncing period
![]() $T=4\unicode[STIX]{x03C0}/\unicode[STIX]{x1D714}_{0}$
, with balances
$T=4\unicode[STIX]{x03C0}/\unicode[STIX]{x1D714}_{0}$
, with balances
![]() $f\sim mg$
and
$f\sim mg$
and
![]() $P\sim mg/\unicode[STIX]{x1D706}^{2}$
. This yields the dimensionless equations for the waves,
$P\sim mg/\unicode[STIX]{x1D706}^{2}$
. This yields the dimensionless equations for the waves,
and droplet dynamics,
for any
![]() $\unicode[STIX]{x1D70F}>0$
. Here, we have defined dimensionless parameters
$\unicode[STIX]{x1D70F}>0$
. Here, we have defined dimensionless parameters
Typical parameter values from table 1 give a reciprocal Reynolds number of
![]() $\unicode[STIX]{x1D716}\approx 0.019$
, a Bond number of
$\unicode[STIX]{x1D716}\approx 0.019$
, a Bond number of
![]() $B\approx 0.102$
,
$B\approx 0.102$
,
![]() $G\approx 1.201$
,
$G\approx 1.201$
,
![]() $M\approx 0.0017$
,
$M\approx 0.0017$
,
![]() $R\approx 0.075$
and
$R\approx 0.075$
and
![]() $\tilde{\unicode[STIX]{x1D708}}_{p}\approx 0.01$
. The droplet radius corresponds to a vibration number of
$\tilde{\unicode[STIX]{x1D708}}_{p}\approx 0.01$
. The droplet radius corresponds to a vibration number of
![]() $\unicode[STIX]{x1D6FA}\equiv 4\unicode[STIX]{x03C0}\sqrt{R^{3}/B}=0.8$
, which minimises the walking threshold
$\unicode[STIX]{x1D6FA}\equiv 4\unicode[STIX]{x03C0}\sqrt{R^{3}/B}=0.8$
, which minimises the walking threshold
![]() $\unicode[STIX]{x1D6E4}_{W}$
for this fluid (Wind-Willassen et al.
Reference Wind-Willassen, Moláček, Harris and Bush2013). The dimensionless potential strength
$\unicode[STIX]{x1D6E4}_{W}$
for this fluid (Wind-Willassen et al.
Reference Wind-Willassen, Moláček, Harris and Bush2013). The dimensionless potential strength
![]() $\tilde{\unicode[STIX]{x1D705}}\sim 10^{-2}$
is a free parameter of both the model and experiments.
$\tilde{\unicode[STIX]{x1D705}}\sim 10^{-2}$
is a free parameter of both the model and experiments.
As we prescribe the periodic vertical dynamics, we must prescribe the phase shift
![]() $\unicode[STIX]{x1D6FD}$
between the vertical motion of the droplet and the waves (this is discussed in § 3.3). This alters the dimensionless effective gravity to
$\unicode[STIX]{x1D6FD}$
between the vertical motion of the droplet and the waves (this is discussed in § 3.3). This alters the dimensionless effective gravity to
![]() $\tilde{g}_{\unicode[STIX]{x1D6E4}}(t)=1-\unicode[STIX]{x1D6E4}\cos (4\unicode[STIX]{x03C0}t+\unicode[STIX]{x1D6FD}).$
$\tilde{g}_{\unicode[STIX]{x1D6E4}}(t)=1-\unicode[STIX]{x1D6E4}\cos (4\unicode[STIX]{x03C0}t+\unicode[STIX]{x1D6FD}).$
3.1 Basis function expansion
The assumption of infinite depth allows us to adapt the ideas of Benjamin & Ursell (Reference Benjamin and Ursell1954), whereby we decompose the wave perturbation
![]() $\unicode[STIX]{x1D702}$
and velocity potential
$\unicode[STIX]{x1D702}$
and velocity potential
![]() $\unicode[STIX]{x1D719}$
in terms of orthogonal eigenfunctions of Laplace’s equation. Specifically, we use Bessel functions
$\unicode[STIX]{x1D719}$
in terms of orthogonal eigenfunctions of Laplace’s equation. Specifically, we use Bessel functions
![]() $\text{J}_{m}(\cdot )$
to pose the expansions
$\text{J}_{m}(\cdot )$
to pose the expansions
where
![]() $\unicode[STIX]{x1D6F7}_{m}(r,\unicode[STIX]{x1D703};k)\equiv \text{J}_{m}(kr)\cos (m\unicode[STIX]{x1D703})$
and
$\unicode[STIX]{x1D6F7}_{m}(r,\unicode[STIX]{x1D703};k)\equiv \text{J}_{m}(kr)\cos (m\unicode[STIX]{x1D703})$
and
![]() $\unicode[STIX]{x1D6F9}_{m}(r,\unicode[STIX]{x1D703};k)\equiv \text{J}_{m}(kr)\sin (m\unicode[STIX]{x1D703})$
satisfy
$\unicode[STIX]{x1D6F9}_{m}(r,\unicode[STIX]{x1D703};k)\equiv \text{J}_{m}(kr)\sin (m\unicode[STIX]{x1D703})$
satisfy
The coefficients
![]() $a_{m}$
,
$a_{m}$
,
![]() $b_{m}$
,
$b_{m}$
,
![]() $c_{m}$
and
$c_{m}$
and
![]() $d_{m}$
may be determined on substitution into (3.1)–(3.3). For clarity, we set
$d_{m}$
may be determined on substitution into (3.1)–(3.3). For clarity, we set
![]() $b_{0}\equiv d_{0}\equiv 0$
since
$b_{0}\equiv d_{0}\equiv 0$
since
![]() $\unicode[STIX]{x1D6F9}_{0}(r,\unicode[STIX]{x1D703};k)\equiv 0$
for all
$\unicode[STIX]{x1D6F9}_{0}(r,\unicode[STIX]{x1D703};k)\equiv 0$
for all
![]() $k\geqslant 0$
.
$k\geqslant 0$
.
By choice of the orthogonal basis functions in (3.8), the continuity equation (2.1) is automatically satisfied. For horizontal droplet position
![]() $(r,\unicode[STIX]{x1D703})=(r_{d}(t),\unicode[STIX]{x1D703}_{d}(t))$
at time
$(r,\unicode[STIX]{x1D703})=(r_{d}(t),\unicode[STIX]{x1D703}_{d}(t))$
at time
![]() $t>0$
and small droplets, we model the droplet impacts at a point. Thus, we prescribe the pressure
$t>0$
and small droplets, we model the droplet impacts at a point. Thus, we prescribe the pressure
where
![]() $f(t)$
is the force applied by the droplet on the surface, which is zero during droplet flight. By exploiting the closure relation
$f(t)$
is the force applied by the droplet on the surface, which is zero during droplet flight. By exploiting the closure relation
![]() $\int _{0}^{\infty }kr\text{J}_{m}(kr)\text{J}_{m}(\unicode[STIX]{x1D709}r)\,\text{d}r=\unicode[STIX]{x1D6FF}(k-\unicode[STIX]{x1D709})$
and trigonometric orthogonality, we expand
$\int _{0}^{\infty }kr\text{J}_{m}(kr)\text{J}_{m}(\unicode[STIX]{x1D709}r)\,\text{d}r=\unicode[STIX]{x1D6FF}(k-\unicode[STIX]{x1D709})$
and trigonometric orthogonality, we expand
where
with eigenfunction norms
![]() $W_{m}=\unicode[STIX]{x03C0}$
if
$W_{m}=\unicode[STIX]{x03C0}$
if
![]() $m>0$
and
$m>0$
and
![]() $W_{0}=2\unicode[STIX]{x03C0}$
. It should be noted that
$W_{0}=2\unicode[STIX]{x03C0}$
. It should be noted that
![]() $q_{0}\equiv 0$
.
$q_{0}\equiv 0$
.
We substitute (3.7)–(3.11) into (3.2)–(3.3) and eliminate
![]() $c_{m}$
and
$c_{m}$
and
![]() $d_{m}$
in favour of
$d_{m}$
in favour of
![]() $a_{m}$
and
$a_{m}$
and
![]() $b_{m}$
. By orthogonality, we obtain a system of inhomogeneous damped Mathieu equations,
$b_{m}$
. By orthogonality, we obtain a system of inhomogeneous damped Mathieu equations,
where
is the wavenumber-dependent homogeneous damped Mathieu differential operator and
The
![]() $\unicode[STIX]{x1D6FE}^{2}(k)$
term gives the additional damping from the vortical boundary layer; this is not present in the work of Eddi et al. (Reference Eddi, Sultan, Moukhtar, Fort, Rossi and Couder2011), who instead replace
$\unicode[STIX]{x1D6FE}^{2}(k)$
term gives the additional damping from the vortical boundary layer; this is not present in the work of Eddi et al. (Reference Eddi, Sultan, Moukhtar, Fort, Rossi and Couder2011), who instead replace
![]() $\unicode[STIX]{x1D716}$
with a phenomenological damping term to match the Faraday threshold.
$\unicode[STIX]{x1D716}$
with a phenomenological damping term to match the Faraday threshold.
3.2 Instantaneous impacts
To close the system, it remains to prescribe
![]() $f(t)$
so that (3.5) is satisfied. To alleviate the difficulty of analysing inhomogeneous Mathieu equations, we simply model the impacts as instantaneous. This gives homogeneous equations for the waves and droplet during flight, and jump conditions at impact. This is the opposite limit to that of Oza et al. (Reference Oza, Rosales and Bush2013), where the droplet glides across the surface of the bath with constant forcing
$f(t)$
so that (3.5) is satisfied. To alleviate the difficulty of analysing inhomogeneous Mathieu equations, we simply model the impacts as instantaneous. This gives homogeneous equations for the waves and droplet during flight, and jump conditions at impact. This is the opposite limit to that of Oza et al. (Reference Oza, Rosales and Bush2013), where the droplet glides across the surface of the bath with constant forcing
![]() $f(t)$
. Assuming that the first impact is at
$f(t)$
. Assuming that the first impact is at
![]() $t=0$
, we define
$t=0$
, we define
where
![]() $t_{n}\equiv n$
for all non-negative integers
$t_{n}\equiv n$
for all non-negative integers
![]() $n$
and
$n$
and
![]() $\unicode[STIX]{x1D6FF}(\cdot )$
is the Dirac delta function. This satisfies periodicity and the integral condition (3.5). We now exploit properties of
$\unicode[STIX]{x1D6FF}(\cdot )$
is the Dirac delta function. This satisfies periodicity and the integral condition (3.5). We now exploit properties of
![]() $\unicode[STIX]{x1D6FF}(\cdot )$
to replace the inhomogeneities in (3.13) with jump conditions.
$\unicode[STIX]{x1D6FF}(\cdot )$
to replace the inhomogeneities in (3.13) with jump conditions.
For physical consistency, we assume that the droplet position
![]() $\boldsymbol{X}(t)$
and wave amplitudes (
$\boldsymbol{X}(t)$
and wave amplitudes (
![]() $a_{m}(t;k)$
and
$a_{m}(t;k)$
and
![]() $b_{m}(t;k)$
) are continuous across all impacts. We denote jumps
$b_{m}(t;k)$
) are continuous across all impacts. We denote jumps
![]() $[Q(t_{n})]_{-}^{+}\equiv Q(t_{n}^{+})-Q(t_{n}^{-})$
for any function of time
$[Q(t_{n})]_{-}^{+}\equiv Q(t_{n}^{+})-Q(t_{n}^{-})$
for any function of time
![]() $Q(t)$
, where
$Q(t)$
, where
![]() $t_{n}^{+}$
and
$t_{n}^{+}$
and
![]() $t_{n}^{-}$
are the right and left limits of
$t_{n}^{-}$
are the right and left limits of
![]() $t_{n}$
respectively. We now integrate the governing equations (3.13) over
$t_{n}$
respectively. We now integrate the governing equations (3.13) over
![]() $t\in [t_{n}^{-},t_{n}^{+}]$
. For all
$t\in [t_{n}^{-},t_{n}^{+}]$
. For all
![]() $n\geqslant 0$
, the first equation gives
$n\geqslant 0$
, the first equation gives
As the droplet position is assumed to be continuous, the sifting property of
![]() $\unicode[STIX]{x1D6FF}(\cdot )$
can be applied to the right-hand side. We use the continuity of
$\unicode[STIX]{x1D6FF}(\cdot )$
can be applied to the right-hand side. We use the continuity of
![]() $a_{m}(t;k)$
to simplify the left-hand side. Hence, (3.13) supply jump conditions
$a_{m}(t;k)$
to simplify the left-hand side. Hence, (3.13) supply jump conditions
where a prime denotes the partial derivative with respect to
![]() $t$
and
$t$
and
![]() $P_{m}(k)=kMG/W_{m}$
.
$P_{m}(k)=kMG/W_{m}$
.
For the droplet dynamics (3.4), we first consider a single impact at
![]() $t=t_{\star }$
. Hence,
$t=t_{\star }$
. Hence,
For
![]() $c=0$
, we may proceed as above to find the jump in
$c=0$
, we may proceed as above to find the jump in
![]() $\boldsymbol{X}^{\prime }(t)$
at
$\boldsymbol{X}^{\prime }(t)$
at
![]() $t=t_{\star }$
. The case
$t=t_{\star }$
. The case
![]() $c>0$
is more delicate; the sifting property cannot be applied as
$c>0$
is more delicate; the sifting property cannot be applied as
![]() $\boldsymbol{X}^{\prime }(t)$
is discontinuous at
$\boldsymbol{X}^{\prime }(t)$
is discontinuous at
![]() $t=t_{\star }$
. Following the method of Catllá et al. (Reference Catllá, Schaeffer, Witelski, Monson and Lin2008), we replace
$t=t_{\star }$
. Following the method of Catllá et al. (Reference Catllá, Schaeffer, Witelski, Monson and Lin2008), we replace
![]() $\unicode[STIX]{x1D6FF}(t-t_{\star })$
with
$\unicode[STIX]{x1D6FF}(t-t_{\star })$
with
where
![]() $\unicode[STIX]{x1D711}(\unicode[STIX]{x1D70F})\geqslant 0$
for all
$\unicode[STIX]{x1D711}(\unicode[STIX]{x1D70F})\geqslant 0$
for all
![]() $\unicode[STIX]{x1D70F}\in \mathbb{R}$
and
$\unicode[STIX]{x1D70F}\in \mathbb{R}$
and
![]() $\int _{-\infty }^{\infty }\unicode[STIX]{x1D711}(\unicode[STIX]{x1D70F})\,\text{d}\unicode[STIX]{x1D70F}=1$
. Hence, the functions
$\int _{-\infty }^{\infty }\unicode[STIX]{x1D711}(\unicode[STIX]{x1D70F})\,\text{d}\unicode[STIX]{x1D70F}=1$
. Hence, the functions
![]() $\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D700}}(\cdot )\rightarrow \unicode[STIX]{x1D6FF}(\cdot )$
pointwise as
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D700}}(\cdot )\rightarrow \unicode[STIX]{x1D6FF}(\cdot )$
pointwise as
![]() $\unicode[STIX]{x1D700}\rightarrow 0$
, except at the jump discontinuity in
$\unicode[STIX]{x1D700}\rightarrow 0$
, except at the jump discontinuity in
![]() $\unicode[STIX]{x1D6FF}(\cdot )$
. This is an appealing formulation, as, physically, no impact is actually instantaneous – it just occurs over a much faster time scale than the dynamics of the rest of the system.
$\unicode[STIX]{x1D6FF}(\cdot )$
. This is an appealing formulation, as, physically, no impact is actually instantaneous – it just occurs over a much faster time scale than the dynamics of the rest of the system.
The idea is to find a solution to (3.20) when
![]() $t>t_{\star }$
with
$t>t_{\star }$
with
![]() $\unicode[STIX]{x1D6FF}(\cdot )$
replaced by
$\unicode[STIX]{x1D6FF}(\cdot )$
replaced by
![]() $\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D700}}(\cdot )$
, and then consider the limit as
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D700}}(\cdot )$
, and then consider the limit as
![]() $\unicode[STIX]{x1D700}\rightarrow 0$
. This determines
$\unicode[STIX]{x1D700}\rightarrow 0$
. This determines
![]() $\boldsymbol{X}^{\prime }(t_{\star }^{+})$
. However, for
$\boldsymbol{X}^{\prime }(t_{\star }^{+})$
. However, for
![]() $t<t_{\star }$
, (3.20) can be solved directly without approximation (as the
$t<t_{\star }$
, (3.20) can be solved directly without approximation (as the
![]() $\unicode[STIX]{x1D6FF}(\cdot )$
terms vanish), which supplies
$\unicode[STIX]{x1D6FF}(\cdot )$
terms vanish), which supplies
![]() $\boldsymbol{X}^{\prime }(t_{\star }^{-})$
. Hence, the jump
$\boldsymbol{X}^{\prime }(t_{\star }^{-})$
. Hence, the jump
![]() $[\boldsymbol{X}^{\prime }(t_{\star })]_{-}^{+}$
is obtained, which is independent of
$[\boldsymbol{X}^{\prime }(t_{\star })]_{-}^{+}$
is obtained, which is independent of
![]() $\unicode[STIX]{x1D711}(\cdot )$
. By generalising the proof of Catllá et al. (Reference Catllá, Schaeffer, Witelski, Monson and Lin2008) (as outlined in appendix A) and extending to periodic impacts, we obtain the jump condition shown in (3.27) below.
$\unicode[STIX]{x1D711}(\cdot )$
. By generalising the proof of Catllá et al. (Reference Catllá, Schaeffer, Witelski, Monson and Lin2008) (as outlined in appendix A) and extending to periodic impacts, we obtain the jump condition shown in (3.27) below.
3.3 Model summary
We have the dimensionless system
where
![]() $P_{m}(k)=kMG/W_{m}$
and
$P_{m}(k)=kMG/W_{m}$
and
![]() $F(c)=1-\exp (-cG\sqrt{R/B})$
. One should note the abuse of notation
$F(c)=1-\exp (-cG\sqrt{R/B})$
. One should note the abuse of notation
![]() $\unicode[STIX]{x1D6F7}_{m}(\boldsymbol{X}(t_{n});k)\equiv \unicode[STIX]{x1D6F7}_{m}(r_{d}(t_{n}),\unicode[STIX]{x1D703}_{d}(t_{n});k)$
(and similarly for
$\unicode[STIX]{x1D6F7}_{m}(\boldsymbol{X}(t_{n});k)\equiv \unicode[STIX]{x1D6F7}_{m}(r_{d}(t_{n}),\unicode[STIX]{x1D703}_{d}(t_{n});k)$
(and similarly for
![]() $\unicode[STIX]{x1D6F9}_{m}$
). The system of jump conditions is self-consistent, with both
$\unicode[STIX]{x1D6F9}_{m}$
). The system of jump conditions is self-consistent, with both
![]() $\unicode[STIX]{x1D702}$
and
$\unicode[STIX]{x1D702}$
and
![]() $\boldsymbol{X}$
continuous across impacts.
$\boldsymbol{X}$
continuous across impacts.
This model has two undefined parameters: the skidding friction
![]() $c$
and the phase shift
$c$
and the phase shift
![]() $\unicode[STIX]{x1D6FD}$
. From the theoretical calculations of Moláček & Bush (Reference Moláček and Bush2013b
),
$\unicode[STIX]{x1D6FD}$
. From the theoretical calculations of Moláček & Bush (Reference Moláček and Bush2013b
),
![]() $c\approx 0.3$
, but the authors consider
$c\approx 0.3$
, but the authors consider
![]() $c\in [0.17,0.33]$
for simulations. Oza et al. (Reference Oza, Rosales and Bush2013) use the lower bound
$c\in [0.17,0.33]$
for simulations. Oza et al. (Reference Oza, Rosales and Bush2013) use the lower bound
![]() $c=0.17$
in the stroboscopic approximation model, which has the opposite impact duration limit to our model. Hence, it is natural to choose the upper bound
$c=0.17$
in the stroboscopic approximation model, which has the opposite impact duration limit to our model. Hence, it is natural to choose the upper bound
![]() $c=0.33$
, which is fixed throughout the paper. The phase shift
$c=0.33$
, which is fixed throughout the paper. The phase shift
![]() $\unicode[STIX]{x1D6FD}$
between bath vibrations and droplet impacts for periodic states arises naturally in models where the droplet vertical dynamics are explicitly modelled (Moláček & Bush Reference Moláček and Bush2013b
; Milewski et al.
Reference Milewski, Galeano-Rios, Nachbin and Bush2015). As we restrict the droplet to periodic impacts, we must choose
$\unicode[STIX]{x1D6FD}$
between bath vibrations and droplet impacts for periodic states arises naturally in models where the droplet vertical dynamics are explicitly modelled (Moláček & Bush Reference Moláček and Bush2013b
; Milewski et al.
Reference Milewski, Galeano-Rios, Nachbin and Bush2015). As we restrict the droplet to periodic impacts, we must choose
![]() $\unicode[STIX]{x1D6FD}$
. We focus on the prevalent
$\unicode[STIX]{x1D6FD}$
. We focus on the prevalent
![]() $(2,1)^{2}$
walking mode, where
$(2,1)^{2}$
walking mode, where
![]() $\unicode[STIX]{x1D6FD}$
has a typical value of
$\unicode[STIX]{x1D6FD}$
has a typical value of
![]() $\unicode[STIX]{x1D6FD}=\unicode[STIX]{x03C0}$
(Milewski et al.
Reference Milewski, Galeano-Rios, Nachbin and Bush2015), which is fixed henceforth. For later works,
$\unicode[STIX]{x1D6FD}=\unicode[STIX]{x03C0}$
(Milewski et al.
Reference Milewski, Galeano-Rios, Nachbin and Bush2015), which is fixed henceforth. For later works,
![]() $c$
and
$c$
and
![]() $\unicode[STIX]{x1D6FD}$
may be tuned when comparing with experimental data.
$\unicode[STIX]{x1D6FD}$
may be tuned when comparing with experimental data.
3.4 Faraday instability
Following Milewski et al. (Reference Milewski, Galeano-Rios, Nachbin and Bush2015) to determine the subharmonic Faraday instability, we look for subharmonic solutions to
![]() ${\mathcal{L}}_{k}a(t;k)=0$
of the form
${\mathcal{L}}_{k}a(t;k)=0$
of the form
![]() $a(t;k)=A\cos (2\unicode[STIX]{x03C0}t)+B\sin (2\unicode[STIX]{x03C0}t)$
. After substitution, higher-order frequencies are neglected, which is equivalent to truncating the Hill matrix. For a non-trivial system, we require
$a(t;k)=A\cos (2\unicode[STIX]{x03C0}t)+B\sin (2\unicode[STIX]{x03C0}t)$
. After substitution, higher-order frequencies are neglected, which is equivalent to truncating the Hill matrix. For a non-trivial system, we require
The function
![]() $\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E4}(k)$
is globally minimised at
$\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E4}(k)$
is globally minimised at
![]() $k=k_{F}$
, where for
$k=k_{F}$
, where for
![]() $\unicode[STIX]{x1D6E4}<\unicode[STIX]{x1D6E4}(k_{F})\equiv \unicode[STIX]{x1D6E4}_{F}$
the subharmonic solutions are stable for any
$\unicode[STIX]{x1D6E4}<\unicode[STIX]{x1D6E4}(k_{F})\equiv \unicode[STIX]{x1D6E4}_{F}$
the subharmonic solutions are stable for any
![]() $k>0$
. By our dimensionless scaling,
$k>0$
. By our dimensionless scaling,
![]() $\unicode[STIX]{x1D706}_{F}\approx 1$
, where
$\unicode[STIX]{x1D706}_{F}\approx 1$
, where
![]() $k_{F}=2\unicode[STIX]{x03C0}/\unicode[STIX]{x1D706}_{F}$
. Although it is known that
$k_{F}=2\unicode[STIX]{x03C0}/\unicode[STIX]{x1D706}_{F}$
. Although it is known that
![]() $\unicode[STIX]{x1D6E4}_{F}$
obtained in this model is not accurate when compared with experiments (Milewski et al.
Reference Milewski, Galeano-Rios, Nachbin and Bush2015), it is usual to use
$\unicode[STIX]{x1D6E4}_{F}$
obtained in this model is not accurate when compared with experiments (Milewski et al.
Reference Milewski, Galeano-Rios, Nachbin and Bush2015), it is usual to use
![]() $\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6E4}_{F}$
as a controlling parameter (Eddi et al.
Reference Eddi, Sultan, Moukhtar, Fort, Rossi and Couder2011). In fact, we show in § 5.3 that the wave field temporal decay rate may be written as a function of
$\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6E4}_{F}$
as a controlling parameter (Eddi et al.
Reference Eddi, Sultan, Moukhtar, Fort, Rossi and Couder2011). In fact, we show in § 5.3 that the wave field temporal decay rate may be written as a function of
![]() $\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6E4}_{F}$
, which justifies our approach for a theoretical investigation.
$\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6E4}_{F}$
, which justifies our approach for a theoretical investigation.
3.5 Discrete-time model
As (3.22)–(3.27) form a homogeneous system with jump conditions, it is natural to reformulate as a discrete-time system. We denote
![]() $\boldsymbol{a}_{n}(k)\equiv (a_{0}(t_{n};k),a_{1}(t_{n};k),\ldots )^{\text{T}}$
and
$\boldsymbol{a}_{n}(k)\equiv (a_{0}(t_{n};k),a_{1}(t_{n};k),\ldots )^{\text{T}}$
and
![]() $\boldsymbol{a}_{n}^{\prime }(k)\equiv (a_{0}^{\prime }(t_{n}^{+};k),a_{1}^{\prime }(t_{n}^{+};k),\ldots )^{\text{T}}$
, and similarly for
$\boldsymbol{a}_{n}^{\prime }(k)\equiv (a_{0}^{\prime }(t_{n}^{+};k),a_{1}^{\prime }(t_{n}^{+};k),\ldots )^{\text{T}}$
, and similarly for
![]() $\boldsymbol{b}_{n}(k)$
and
$\boldsymbol{b}_{n}(k)$
and
![]() $\boldsymbol{b}_{n}^{\prime }(k)$
. We also write the eigenfunctions as vectors
$\boldsymbol{b}_{n}^{\prime }(k)$
. We also write the eigenfunctions as vectors
![]() $\unicode[STIX]{x1D731}(\cdot ;k)=(\unicode[STIX]{x1D6F7}_{0}(\cdot ;k),\unicode[STIX]{x1D6F7}_{1}(\cdot ;k),\ldots )^{\text{T}}$
, and similarly for
$\unicode[STIX]{x1D731}(\cdot ;k)=(\unicode[STIX]{x1D6F7}_{0}(\cdot ;k),\unicode[STIX]{x1D6F7}_{1}(\cdot ;k),\ldots )^{\text{T}}$
, and similarly for
![]() $\unicode[STIX]{x1D733}(\cdot ;k)$
, with
$\unicode[STIX]{x1D733}(\cdot ;k)$
, with
![]() $\unicode[STIX]{x1D64B}(k)$
a diagonal matrix with elements
$\unicode[STIX]{x1D64B}(k)$
a diagonal matrix with elements
![]() $P_{m}(k)$
. By periodicity of the Mathieu operator
$P_{m}(k)$
. By periodicity of the Mathieu operator
![]() ${\mathcal{L}}_{k}$
, we numerically construct the principal fundamental matrix
${\mathcal{L}}_{k}$
, we numerically construct the principal fundamental matrix
![]() $\unicode[STIX]{x1D648}_{k}(\unicode[STIX]{x1D6E4})$
over the interval
$\unicode[STIX]{x1D648}_{k}(\unicode[STIX]{x1D6E4})$
over the interval
![]() $(0,1)$
. As
$(0,1)$
. As
![]() ${\mathcal{L}}_{k}$
is independent of the Bessel order,
${\mathcal{L}}_{k}$
is independent of the Bessel order,
![]() $\unicode[STIX]{x1D648}_{k}$
has block diagonal form
$\unicode[STIX]{x1D648}_{k}$
has block diagonal form
where
![]() $\unicode[STIX]{x1D644}$
is the infinite identity matrix. The principal fundamental matrix
$\unicode[STIX]{x1D644}$
is the infinite identity matrix. The principal fundamental matrix
![]() $\unicode[STIX]{x1D641}(\tilde{\unicode[STIX]{x1D705}})$
corresponding to the droplet dynamics is constructed by analytically solving (3.24).
$\unicode[STIX]{x1D641}(\tilde{\unicode[STIX]{x1D705}})$
corresponding to the droplet dynamics is constructed by analytically solving (3.24).
We reformulate (3.22)–(3.27) as an efficient one-step map with stages for droplet position
![]() $\boldsymbol{X}_{n}\equiv \boldsymbol{X}(t_{n})$
and velocity
$\boldsymbol{X}_{n}\equiv \boldsymbol{X}(t_{n})$
and velocity
![]() $\boldsymbol{X}_{n}^{\prime }\equiv \boldsymbol{X}^{\prime }(t_{n}^{+})$
.
$\boldsymbol{X}_{n}^{\prime }\equiv \boldsymbol{X}^{\prime }(t_{n}^{+})$
.
-
(i) Use
 $\boldsymbol{X}_{n}$
and
$\boldsymbol{X}_{n}$
and
 $\boldsymbol{X}_{n}^{\prime }$
to compute
$\boldsymbol{X}_{n}^{\prime }$
to compute
 $\boldsymbol{X}_{n+1}$
and
$\boldsymbol{X}_{n+1}$
and
 $\tilde{\boldsymbol{X}}^{\prime }\equiv \boldsymbol{X}^{\prime }(t_{n+1}^{-})$
: (3.30)
$\tilde{\boldsymbol{X}}^{\prime }\equiv \boldsymbol{X}^{\prime }(t_{n+1}^{-})$
: (3.30) $$\begin{eqnarray}\left[\begin{array}{@{}c@{}}\boldsymbol{X}_{n+1}\\ \tilde{\boldsymbol{X}}^{\prime }\end{array}\right]=\unicode[STIX]{x1D641}(\tilde{\unicode[STIX]{x1D705}})\left[\begin{array}{@{}c@{}}\boldsymbol{X}_{n}\\ \boldsymbol{X}_{n}^{\prime }\end{array}\right].\end{eqnarray}$$
$$\begin{eqnarray}\left[\begin{array}{@{}c@{}}\boldsymbol{X}_{n+1}\\ \tilde{\boldsymbol{X}}^{\prime }\end{array}\right]=\unicode[STIX]{x1D641}(\tilde{\unicode[STIX]{x1D705}})\left[\begin{array}{@{}c@{}}\boldsymbol{X}_{n}\\ \boldsymbol{X}_{n}^{\prime }\end{array}\right].\end{eqnarray}$$
-
(ii) Update wave amplitudes including jump conditions
 $\forall k>0$
(similarly for
$\forall k>0$
(similarly for
 $\boldsymbol{b}_{n}(k)$
): (3.31)
$\boldsymbol{b}_{n}(k)$
): (3.31) $$\begin{eqnarray}\left[\begin{array}{@{}c@{}}\boldsymbol{a}_{n+1}(k)\\ \boldsymbol{a}_{n+1}^{\prime }(k)\end{array}\right]=\unicode[STIX]{x1D648}_{k}(\unicode[STIX]{x1D6E4})\left[\begin{array}{@{}c@{}}\boldsymbol{a}_{n}(k)\\ \boldsymbol{a}_{n}^{\prime }(k)\end{array}\right]-\left[\begin{array}{@{}c@{}}\mathbf{0}\\ \unicode[STIX]{x1D64B}(k)\unicode[STIX]{x1D731}(\boldsymbol{X}_{n+1};k)\end{array}\right].\end{eqnarray}$$
$$\begin{eqnarray}\left[\begin{array}{@{}c@{}}\boldsymbol{a}_{n+1}(k)\\ \boldsymbol{a}_{n+1}^{\prime }(k)\end{array}\right]=\unicode[STIX]{x1D648}_{k}(\unicode[STIX]{x1D6E4})\left[\begin{array}{@{}c@{}}\boldsymbol{a}_{n}(k)\\ \boldsymbol{a}_{n}^{\prime }(k)\end{array}\right]-\left[\begin{array}{@{}c@{}}\mathbf{0}\\ \unicode[STIX]{x1D64B}(k)\unicode[STIX]{x1D731}(\boldsymbol{X}_{n+1};k)\end{array}\right].\end{eqnarray}$$
-
(iii) Apply droplet jump conditions:
(3.32) $$\begin{eqnarray}\boldsymbol{X}_{n+1}^{\prime }=(1-F(c))\tilde{\boldsymbol{X}}^{\prime }-\frac{F(c)}{c}\sqrt{\frac{B}{R}}\unicode[STIX]{x1D735}\unicode[STIX]{x1D702}(\boldsymbol{X}_{n+1},t_{n+1}).\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{X}_{n+1}^{\prime }=(1-F(c))\tilde{\boldsymbol{X}}^{\prime }-\frac{F(c)}{c}\sqrt{\frac{B}{R}}\unicode[STIX]{x1D735}\unicode[STIX]{x1D702}(\boldsymbol{X}_{n+1},t_{n+1}).\end{eqnarray}$$
3.6 Numerical implementation
The remainder of this work involves simulating and finding fixed points of the system (3.30)–(3.32), both of which require suitable truncations in the wavenumber
![]() $k>0$
and Bessel mode
$k>0$
and Bessel mode
![]() $m\in \mathbb{N}$
. For any impact time
$m\in \mathbb{N}$
. For any impact time
![]() $t_{n}$
, the wavenumbers are generally peaked around
$t_{n}$
, the wavenumbers are generally peaked around
![]() $k=k_{F}$
, with the peak becoming narrower as
$k=k_{F}$
, with the peak becoming narrower as
![]() $\unicode[STIX]{x1D6E4}\rightarrow \unicode[STIX]{x1D6E4}_{F}^{-}$
, which can be analysed from Floquet analysis of the damped Mathieu equation. This determines the refinement and truncation in
$\unicode[STIX]{x1D6E4}\rightarrow \unicode[STIX]{x1D6E4}_{F}^{-}$
, which can be analysed from Floquet analysis of the damped Mathieu equation. This determines the refinement and truncation in
![]() $k$
, which is successively reduced until the change in the numerical solution of the fixed points becomes negligible. Away from the Faraday threshold, a reasonably coarse mesh is sufficient, with
$k$
, which is successively reduced until the change in the numerical solution of the fixed points becomes negligible. Away from the Faraday threshold, a reasonably coarse mesh is sufficient, with
![]() $\unicode[STIX]{x1D6FF}k\sim 0.2$
and
$\unicode[STIX]{x1D6FF}k\sim 0.2$
and
![]() $k\in [k_{F}/2,3k_{F}/2]$
, where
$k\in [k_{F}/2,3k_{F}/2]$
, where
![]() $k_{F}$
is a mesh point. Integrals over
$k_{F}$
is a mesh point. Integrals over
![]() $k$
(e.g. for finding
$k$
(e.g. for finding
![]() $\unicode[STIX]{x1D735}\unicode[STIX]{x1D702}$
) are evaluated using the trapezium rule, which is well suited to capturing the peaked behaviour in
$\unicode[STIX]{x1D735}\unicode[STIX]{x1D702}$
) are evaluated using the trapezium rule, which is well suited to capturing the peaked behaviour in
![]() $k$
.
$k$
.
Truncation of the Bessel modes follows from the asymptotic behaviour of Bessel functions, namely
![]() $\text{J}_{m}(z)\sim (1/m!)(z/2)^{m}$
for
$\text{J}_{m}(z)\sim (1/m!)(z/2)^{m}$
for
![]() $0<z\ll \sqrt{m+1}$
. Hence, for orbital solutions or simulations with a central force, the maximum radial extent of the droplet can be estimated, which provides a good guide for the truncation
$0<z\ll \sqrt{m+1}$
. Hence, for orbital solutions or simulations with a central force, the maximum radial extent of the droplet can be estimated, which provides a good guide for the truncation
![]() $m\in \{0,1,\ldots ,m^{\star }\}$
. For walking dynamics, the Floquet exponents provide an estimate of how the temporal decay affects the number of past impacts that contribute to the current wave field (this is the system ‘memory’, as discussed in § 5.3), where we typically have
$m\in \{0,1,\ldots ,m^{\star }\}$
. For walking dynamics, the Floquet exponents provide an estimate of how the temporal decay affects the number of past impacts that contribute to the current wave field (this is the system ‘memory’, as discussed in § 5.3), where we typically have
![]() $m^{\star }=15$
for
$m^{\star }=15$
for
![]() $\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6E4}_{F}\approx 0.81$
but
$\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6E4}_{F}\approx 0.81$
but
![]() $m^{\star }\approx 50$
for
$m^{\star }\approx 50$
for
![]() $\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6E4}_{F}\approx 0.95$
. The accuracy of this truncation can be easily checked a posteriori, with
$\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6E4}_{F}\approx 0.95$
. The accuracy of this truncation can be easily checked a posteriori, with
![]() $m^{\star }$
increased until there is a negligible change in the numerical solution.
$m^{\star }$
increased until there is a negligible change in the numerical solution.
For simulation efficiency, Bessel functions are only evaluated once per impact period, with derivatives calculated using the identity
![]() $\text{J}_{m}^{\prime }(z)=(1/2)(\text{J}_{m-1}(z)-\text{J}_{m+1}(z))$
. We typically simulate 1000 impacts per second on a standard desktop machine using MATLAB.
$\text{J}_{m}^{\prime }(z)=(1/2)(\text{J}_{m-1}(z)-\text{J}_{m+1}(z))$
. We typically simulate 1000 impacts per second on a standard desktop machine using MATLAB.
4 Bouncing states
We now find bouncing states of (3.22)–(3.27) with
![]() $\tilde{\unicode[STIX]{x1D705}}=0$
. By translational invariance, we assume that the drop bounces at the origin (
$\tilde{\unicode[STIX]{x1D705}}=0$
. By translational invariance, we assume that the drop bounces at the origin (
![]() $\boldsymbol{X}\equiv \mathbf{0}$
) with radially symmetric wave field
$\boldsymbol{X}\equiv \mathbf{0}$
) with radially symmetric wave field
This ensures that the droplet receives no horizontal kick at impact, and so remains a bouncer. We demand a periodic wave field, with
![]() $\unicode[STIX]{x1D702}(\boldsymbol{x},t_{n+1})=\unicode[STIX]{x1D702}(\boldsymbol{x},t_{n})$
and
$\unicode[STIX]{x1D702}(\boldsymbol{x},t_{n+1})=\unicode[STIX]{x1D702}(\boldsymbol{x},t_{n})$
and
![]() $\unicode[STIX]{x1D702}_{t}(\boldsymbol{x},t_{n+1}^{+})=\unicode[STIX]{x1D702}_{t}(\boldsymbol{x},t_{n}^{+})$
for all
$\unicode[STIX]{x1D702}_{t}(\boldsymbol{x},t_{n+1}^{+})=\unicode[STIX]{x1D702}_{t}(\boldsymbol{x},t_{n}^{+})$
for all
![]() $n$
and all
$n$
and all
![]() $\boldsymbol{x}\in \mathbb{R}^{2}$
. By orthogonality, the wave amplitudes must satisfy
$\boldsymbol{x}\in \mathbb{R}^{2}$
. By orthogonality, the wave amplitudes must satisfy
for all
![]() $t_{n}$
and
$t_{n}$
and
![]() $\forall k\geqslant 0$
. By periodicity, it is sufficient to consider the interval
$\forall k\geqslant 0$
. By periodicity, it is sufficient to consider the interval
![]() $t\in [0,1]$
.
$t\in [0,1]$
.
By considering (3.31) and the form of
![]() $\unicode[STIX]{x1D648}_{k}(\unicode[STIX]{x1D6E4})$
, it remains to solve the linear system
$\unicode[STIX]{x1D648}_{k}(\unicode[STIX]{x1D6E4})$
, it remains to solve the linear system
where
![]() $\unicode[STIX]{x1D644}_{2}\in \mathbb{R}^{2\times 2}$
is the identity matrix and we used
$\unicode[STIX]{x1D644}_{2}\in \mathbb{R}^{2\times 2}$
is the identity matrix and we used
![]() $\unicode[STIX]{x1D6F7}_{0}(\mathbf{0};k)=1$
,
$\unicode[STIX]{x1D6F7}_{0}(\mathbf{0};k)=1$
,
![]() $\forall k$
.
$\forall k$
.
4.1 Stability analysis
To determine the walking threshold
![]() $\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E4}_{W}$
, we perform linear stability analysis of the periodic bouncing system. The aim is to construct a one-step matrix map
$\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E4}_{W}$
, we perform linear stability analysis of the periodic bouncing system. The aim is to construct a one-step matrix map
![]() $\unicode[STIX]{x1D64F}(\unicode[STIX]{x1D6E4})$
for the perturbed system, where stability is determined by the spectral radius
$\unicode[STIX]{x1D64F}(\unicode[STIX]{x1D6E4})$
for the perturbed system, where stability is determined by the spectral radius
![]() $\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D64F})$
. We denote the steady state by
$\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D64F})$
. We denote the steady state by
![]() $\boldsymbol{X}=\hat{\boldsymbol{X}}$
,
$\boldsymbol{X}=\hat{\boldsymbol{X}}$
,
![]() $a_{m}=\hat{a}_{m}$
and
$a_{m}=\hat{a}_{m}$
and
![]() $b_{m}=\hat{b}_{m}$
, where, for bouncing at the origin,
$b_{m}=\hat{b}_{m}$
, where, for bouncing at the origin,
![]() $\hat{\boldsymbol{X}}\equiv \mathbf{0}$
,
$\hat{\boldsymbol{X}}\equiv \mathbf{0}$
,
![]() $\hat{a}_{m}\equiv \hat{b}_{m}\equiv 0$
for all
$\hat{a}_{m}\equiv \hat{b}_{m}\equiv 0$
for all
![]() $m\geqslant 1$
, and
$m\geqslant 1$
, and
![]() $\hat{b}_{0}\equiv 0$
. We then consider small perturbations
$\hat{b}_{0}\equiv 0$
. We then consider small perturbations
where we assume that
![]() $|\tilde{a}_{m}/\hat{a}_{0}|\sim |\tilde{b}_{m}/\hat{a}_{0}|\sim ||\unicode[STIX]{x1D750}||\ll 1$
. By including an explicit perturbation to the wave field, we consider a more general perturbation than Oza et al. (Reference Oza, Rosales and Bush2013).
$|\tilde{a}_{m}/\hat{a}_{0}|\sim |\tilde{b}_{m}/\hat{a}_{0}|\sim ||\unicode[STIX]{x1D750}||\ll 1$
. By including an explicit perturbation to the wave field, we consider a more general perturbation than Oza et al. (Reference Oza, Rosales and Bush2013).
The system is linearised via the jump conditions (3.25)–(3.27), giving
The Hessian matrix of the steady-state wave field at droplet impact is
![]() $\unicode[STIX]{x1D643}(\unicode[STIX]{x1D6E4})$
and
$\unicode[STIX]{x1D643}(\unicode[STIX]{x1D6E4})$
and
Equations (4.6)–(4.8) are simplified considerably by noting that
for
![]() $m\neq 1$
. Hence, for
$m\neq 1$
. Hence, for
![]() $m\neq 1$
, the jump conditions for
$m\neq 1$
, the jump conditions for
![]() $\tilde{a}_{m}$
,
$\tilde{a}_{m}$
,
![]() $\tilde{b}_{m}$
and
$\tilde{b}_{m}$
and
![]() $\unicode[STIX]{x1D750}$
are all independent of each other (to
$\unicode[STIX]{x1D750}$
are all independent of each other (to
![]() $O(||\unicode[STIX]{x1D750}||)$
). Therefore, the perturbations
$O(||\unicode[STIX]{x1D750}||)$
). Therefore, the perturbations
![]() $\tilde{a}_{m}$
,
$\tilde{a}_{m}$
,
![]() $\tilde{b}_{m}$
(
$\tilde{b}_{m}$
(
![]() $m\neq 1$
) each decouple from the system. As they are unexcited solutions to the damped Mathieu equation with
$m\neq 1$
) each decouple from the system. As they are unexcited solutions to the damped Mathieu equation with
![]() $\unicode[STIX]{x1D6E4}<\unicode[STIX]{x1D6E4}_{F}$
, they are stable and hence are neglected from the stability analysis.
$\unicode[STIX]{x1D6E4}<\unicode[STIX]{x1D6E4}_{F}$
, they are stable and hence are neglected from the stability analysis.
Using the linearised jump conditions with matrices
![]() $\unicode[STIX]{x1D648}_{k}(\unicode[STIX]{x1D6E4})$
and
$\unicode[STIX]{x1D648}_{k}(\unicode[STIX]{x1D6E4})$
and
![]() $\unicode[STIX]{x1D641}(0)$
, we construct a discrete-time linear map for all variables, given by the matrix
$\unicode[STIX]{x1D641}(0)$
, we construct a discrete-time linear map for all variables, given by the matrix
![]() $\unicode[STIX]{x1D64F}(\unicode[STIX]{x1D6E4})$
. The system is neutrally stable if the spectral radius
$\unicode[STIX]{x1D64F}(\unicode[STIX]{x1D6E4})$
. The system is neutrally stable if the spectral radius
![]() $\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D64F})=1$
, and unstable if
$\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D64F})=1$
, and unstable if
![]() $\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D64F})>1$
. The walking threshold
$\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D64F})>1$
. The walking threshold
![]() $\unicode[STIX]{x1D6E4}_{W}$
is the largest
$\unicode[STIX]{x1D6E4}_{W}$
is the largest
![]() $\unicode[STIX]{x1D6E4}$
such that
$\unicode[STIX]{x1D6E4}$
such that
![]() $\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D64F})=1$
. By the translational invariance of the system, there always exists an eigenvalue
$\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D64F})=1$
. By the translational invariance of the system, there always exists an eigenvalue
![]() $\unicode[STIX]{x1D707}$
of
$\unicode[STIX]{x1D707}$
of
![]() $\unicode[STIX]{x1D64F}$
such that
$\unicode[STIX]{x1D64F}$
such that
![]() $\unicode[STIX]{x1D707}=1$
, which prevents us from obtaining asymptotically stable solutions
$\unicode[STIX]{x1D707}=1$
, which prevents us from obtaining asymptotically stable solutions
![]() $(\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D64F})<1)$
in the absence of a central force.
$(\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D64F})<1)$
in the absence of a central force.
5 Steady walking states
By extension, we now find steady walking states and analyse their stability. By rotational and translational invariance, we consider steady walking along the
![]() $x$
-axis in the direction of increasing
$x$
-axis in the direction of increasing
![]() $x$
, with
$x$
, with
![]() $\boldsymbol{X}(t_{0})=\mathbf{0}$
(
$\boldsymbol{X}(t_{0})=\mathbf{0}$
(
![]() $t_{0}=0$
). By symmetry,
$t_{0}=0$
). By symmetry,
![]() $b_{m}\equiv 0$
,
$b_{m}\equiv 0$
,
![]() $\forall m$
.
$\forall m$
.
We denote
![]() $0<\unicode[STIX]{x1D6FF}x\equiv X(t_{n+1})-X(t_{n})$
for all
$0<\unicode[STIX]{x1D6FF}x\equiv X(t_{n+1})-X(t_{n})$
for all
![]() $t_{n}$
, where
$t_{n}$
, where
![]() $\boldsymbol{X}(t)=(X(t),0)$
. For the wave field to follow the droplet between impacts, Graf’s addition theorem (Abramowitz & Stegun Reference Abramowitz and Stegun1964) supplies the requirement
$\boldsymbol{X}(t)=(X(t),0)$
. For the wave field to follow the droplet between impacts, Graf’s addition theorem (Abramowitz & Stegun Reference Abramowitz and Stegun1964) supplies the requirement
and similarly for the first time derivatives. Hence, we have a discrete-time map
where
![]() $\unicode[STIX]{x1D63C}(k;\unicode[STIX]{x1D6FF}x)$
is an infinite matrix given by (5.1)–(5.2). As
$\unicode[STIX]{x1D63C}(k;\unicode[STIX]{x1D6FF}x)$
is an infinite matrix given by (5.1)–(5.2). As
![]() $\unicode[STIX]{x1D63C}(k;0)=\unicode[STIX]{x1D644}$
, (5.3)–(5.4) simplify to the periodicity requirement (4.2)–(4.3) for a bouncing droplet.
$\unicode[STIX]{x1D63C}(k;0)=\unicode[STIX]{x1D644}$
, (5.3)–(5.4) simplify to the periodicity requirement (4.2)–(4.3) for a bouncing droplet.
For steady walking, we require
![]() $\boldsymbol{X}^{\prime }(t_{n}^{+})=\boldsymbol{V}_{0}\equiv (V,0)$
for all
$\boldsymbol{X}^{\prime }(t_{n}^{+})=\boldsymbol{V}_{0}\equiv (V,0)$
for all
![]() $t_{n}$
, for some unknown
$t_{n}$
, for some unknown
![]() $V>0$
. Solving (3.24) with
$V>0$
. Solving (3.24) with
![]() $\tilde{\unicode[STIX]{x1D705}}=0$
for
$\tilde{\unicode[STIX]{x1D705}}=0$
for
![]() $t\in [t_{n},t_{n+1} )$
gives
$t\in [t_{n},t_{n+1} )$
gives
For
![]() $\boldsymbol{X}^{\prime }(t_{n+1}^{+})=\boldsymbol{V}_{0}$
, the jump condition (3.27) and (5.6) give the requirement
$\boldsymbol{X}^{\prime }(t_{n+1}^{+})=\boldsymbol{V}_{0}$
, the jump condition (3.27) and (5.6) give the requirement
By the assumed periodicity of the wave field when centred at the droplet,
![]() $\unicode[STIX]{x1D735}\unicode[STIX]{x1D702}(\boldsymbol{X}(t_{n}),t_{n})$
is constant for all
$\unicode[STIX]{x1D735}\unicode[STIX]{x1D702}(\boldsymbol{X}(t_{n}),t_{n})$
is constant for all
![]() $t_{n}$
. Hence, using (4.10) to simplify the wave field gradient, we require
$t_{n}$
. Hence, using (4.10) to simplify the wave field gradient, we require
where
![]() $\unicode[STIX]{x1D735}\unicode[STIX]{x1D6F7}_{1}(\mathbf{0};k)=(k/2,0)^{\text{T}}$
. From the
$\unicode[STIX]{x1D735}\unicode[STIX]{x1D6F7}_{1}(\mathbf{0};k)=(k/2,0)^{\text{T}}$
. From the
![]() $x$
-components of (5.5) and (5.8),
$x$
-components of (5.5) and (5.8),
![]() $\unicode[STIX]{x1D6FF}x$
must satisfy
$\unicode[STIX]{x1D6FF}x$
must satisfy
To progress, we use the discrete map for the wave amplitudes (3.31). By periodicity and translational invariance, it is sufficient to consider
![]() $t\in [0,1]$
. Conditions (5.3)–(5.4) are thus equivalent to solving the linear system
$t\in [0,1]$
. Conditions (5.3)–(5.4) are thus equivalent to solving the linear system
for all
![]() $k\geqslant 0$
, where
$k\geqslant 0$
, where
![]() $\unicode[STIX]{x1D6FF}x$
is determined by (5.9). The block matrix form of this system allows for quick numerical solution, with the walking speed
$\unicode[STIX]{x1D6FF}x$
is determined by (5.9). The block matrix form of this system allows for quick numerical solution, with the walking speed
![]() $\unicode[STIX]{x1D6FF}x$
shown in figure 1(a).
$\unicode[STIX]{x1D6FF}x$
shown in figure 1(a).
To shed light on this bifurcation, we consider the average energy of the wave field across one period. As derived in appendix B, we compute the change in energy due to the existence of the waves formed by the droplet. This cannot be computed in the models of Moláček & Bush (Reference Moláček and Bush2013b
) and Oza et al. (Reference Oza, Rosales and Bush2013), as the single-wavenumber (
![]() $k_{F}$
) approximation gives insufficient decay at infinity. The dimensionless energy perturbation
$k_{F}$
) approximation gives insufficient decay at infinity. The dimensionless energy perturbation
![]() $E$
as given in (B 7) is shown in figure 1(b), demonstrating that the wave field of a walker requires less energy than that of the corresponding unstable bouncer. We neglect the horizontal kinetic energy of the droplet as it is significantly smaller than the wave field energy for all walking speeds. Furthermore, the assumed periodicity of
$E$
as given in (B 7) is shown in figure 1(b), demonstrating that the wave field of a walker requires less energy than that of the corresponding unstable bouncer. We neglect the horizontal kinetic energy of the droplet as it is significantly smaller than the wave field energy for all walking speeds. Furthermore, the assumed periodicity of
![]() $Z(t)$
gives a constant droplet vertical energy (which balances the wave field energy) for both bouncing and walking.
$Z(t)$
gives a constant droplet vertical energy (which balances the wave field energy) for both bouncing and walking.

Figure 1. (a) Average walking speed
![]() $\unicode[STIX]{x1D6FF}x$
for complete numerical method (black) and approximation valid only for
$\unicode[STIX]{x1D6FF}x$
for complete numerical method (black) and approximation valid only for
![]() $0<\unicode[STIX]{x1D6FF}x\ll 1$
(grey). By the non-dimensionalisation,
$0<\unicode[STIX]{x1D6FF}x\ll 1$
(grey). By the non-dimensionalisation,
![]() $\unicode[STIX]{x1D6FF}x$
is the average walking speed relative to the phase speed of the waves. (b) The average wave field energy for a bouncer (black) and walker (grey), with a bifurcation at
$\unicode[STIX]{x1D6FF}x$
is the average walking speed relative to the phase speed of the waves. (b) The average wave field energy for a bouncer (black) and walker (grey), with a bifurcation at
![]() $\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E4}_{W}$
.
$\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E4}_{W}$
.
5.1 Stability analysis
The stability analysis of a walker is similar to that of a bouncer and therefore we do not give the details. The main difference is that we use Graf’s addition theorem (Abramowitz & Stegun Reference Abramowitz and Stegun1964) to map the wave amplitude perturbation variables so that they are centred on the steady-state droplet position at each impact.
Following Oza et al. (Reference Oza, Rosales and Bush2013), we consider general perturbations, and perturbations to the droplet in the direction of motion. In the former case, the walking is unstable. Physically, this corresponds to a new walker forming after an initial transient, but in a new direction. The latter case is achieved by noting that
![]() $\unicode[STIX]{x1D6F9}_{m}\equiv 0$
along the
$\unicode[STIX]{x1D6F9}_{m}\equiv 0$
along the
![]() $x$
-axis, so the linearised jumps for the perturbation coefficients
$x$
-axis, so the linearised jumps for the perturbation coefficients
![]() $\tilde{b}_{m}$
will be zero for an in-line perturbation. Furthermore,
$\tilde{b}_{m}$
will be zero for an in-line perturbation. Furthermore,
![]() $\unicode[STIX]{x2202}_{x}\unicode[STIX]{x1D6F9}_{m}\equiv 0$
(for all
$\unicode[STIX]{x2202}_{x}\unicode[STIX]{x1D6F9}_{m}\equiv 0$
(for all
![]() $m$
) along the
$m$
) along the
![]() $x$
-axis, so the
$x$
-axis, so the
![]() $\tilde{b}_{m}$
terms do not contribute to the linearised droplet perturbation jump condition. Hence, the
$\tilde{b}_{m}$
terms do not contribute to the linearised droplet perturbation jump condition. Hence, the
![]() $\tilde{b}_{m}$
terms decouple from the perturbed system and can be neglected as they are stable solutions to the Mathieu equation. In this case, the walker is neutrally stable, where an eigenvalue of 1 always exists due to the translational invariance of the problem. This agrees with experiments and also the model of Oza et al. (Reference Oza, Rosales and Bush2013), whose analysis is restricted to lateral and in-line perturbations.
$\tilde{b}_{m}$
terms decouple from the perturbed system and can be neglected as they are stable solutions to the Mathieu equation. In this case, the walker is neutrally stable, where an eigenvalue of 1 always exists due to the translational invariance of the problem. This agrees with experiments and also the model of Oza et al. (Reference Oza, Rosales and Bush2013), whose analysis is restricted to lateral and in-line perturbations.
5.2 Slow-walking analysis
As observed by Protière et al. (Reference Protière, Boudaoud and Couder2006), there is a supercritical bifurcation at the walking threshold, where the walking speed grows like
![]() $(\unicode[STIX]{x1D6E4}-\unicode[STIX]{x1D6E4}_{W})^{1/2}$
. This behaviour has been captured in the trajectory equation of Oza et al. (Reference Oza, Rosales and Bush2013). We explore the slow-walking speed in terms of the distance between impacts
$(\unicode[STIX]{x1D6E4}-\unicode[STIX]{x1D6E4}_{W})^{1/2}$
. This behaviour has been captured in the trajectory equation of Oza et al. (Reference Oza, Rosales and Bush2013). We explore the slow-walking speed in terms of the distance between impacts
![]() $\unicode[STIX]{x1D6FF}x$
, which is the average walking speed in dimensionless variables. For
$\unicode[STIX]{x1D6FF}x$
, which is the average walking speed in dimensionless variables. For
![]() $0<\unicode[STIX]{x1D6FF}x\ll 1$
, we consider asymptotic expansions of the form
$0<\unicode[STIX]{x1D6FF}x\ll 1$
, we consider asymptotic expansions of the form
for all
![]() $m\geqslant 0$
. By the Frobenius series for Bessel functions, we have
$m\geqslant 0$
. By the Frobenius series for Bessel functions, we have
These expansions are valid for
![]() $k/2=O(1)$
. As the least-damped wavenumber
$k/2=O(1)$
. As the least-damped wavenumber
![]() $k_{F}$
satisfies
$k_{F}$
satisfies
![]() $k_{F}/2\approx \unicode[STIX]{x03C0}=O(1)$
, and wavenumbers far away from
$k_{F}/2\approx \unicode[STIX]{x03C0}=O(1)$
, and wavenumbers far away from
![]() $k_{F}$
correspond to negligible wave amplitudes, this assumption is valid. We prove that
$k_{F}$
correspond to negligible wave amplitudes, this assumption is valid. We prove that
![]() $\unicode[STIX]{x1D6E4}_{1}=0$
and verify numerically that
$\unicode[STIX]{x1D6E4}_{1}=0$
and verify numerically that
![]() $\unicode[STIX]{x1D6E4}_{2}>0$
, which gives the desired bifurcation.
$\unicode[STIX]{x1D6E4}_{2}>0$
, which gives the desired bifurcation.
Substituting the asymptotic expansions into the map (5.1)–(5.2), the Mathieu equation (3.22) and jump condition (3.25), and equating powers of
![]() $\unicode[STIX]{x1D6FF}x$
, a system of differential equations with initial and jump conditions is obtained, all of the general form
$\unicode[STIX]{x1D6FF}x$
, a system of differential equations with initial and jump conditions is obtained, all of the general form
Here,
![]() ${\mathcal{H}}$
,
${\mathcal{H}}$
,
![]() ${\mathcal{B}}$
,
${\mathcal{B}}$
,
![]() ${\mathcal{B}}^{\prime }$
and
${\mathcal{B}}^{\prime }$
and
![]() ${\mathcal{J}}$
are inhomogeneities, and
${\mathcal{J}}$
are inhomogeneities, and
![]() ${\mathcal{L}}_{k}^{\unicode[STIX]{x1D6E4}_{W}}$
is the damped Mathieu differential operator with
${\mathcal{L}}_{k}^{\unicode[STIX]{x1D6E4}_{W}}$
is the damped Mathieu differential operator with
![]() $\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E4}_{W}$
. By (5.3)–(5.4), the map for the wave amplitude derivatives is the same as that for the wave amplitudes themselves. Hence, all terms in
$\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E4}_{W}$
. By (5.3)–(5.4), the map for the wave amplitude derivatives is the same as that for the wave amplitudes themselves. Hence, all terms in
![]() ${\mathcal{B}}$
of the form
${\mathcal{B}}$
of the form
![]() $a(0;k)$
are replaced by
$a(0;k)$
are replaced by
![]() $a^{\prime }(0^{+};k)$
in
$a^{\prime }(0^{+};k)$
in
![]() ${\mathcal{B}}^{\prime }$
, so for notational efficiency, we do not state
${\mathcal{B}}^{\prime }$
, so for notational efficiency, we do not state
![]() ${\mathcal{B}}^{\prime }$
explicitly.
${\mathcal{B}}^{\prime }$
explicitly.
First, we note that for
![]() $\unicode[STIX]{x1D6FF}x=0$
, we have a bouncer at the walking threshold, so the wave field is radially symmetric, giving
$\unicode[STIX]{x1D6FF}x=0$
, we have a bouncer at the walking threshold, so the wave field is radially symmetric, giving
![]() $a_{m}^{(0)}\equiv 0$
for
$a_{m}^{(0)}\equiv 0$
for
![]() $m\geqslant 1$
. This is verified by noting that
$m\geqslant 1$
. This is verified by noting that
![]() ${\mathcal{H}}_{m}^{(0)}={\mathcal{B}}_{m}^{(0)}={\mathcal{J}}_{m}^{(0)}=0$
for all
${\mathcal{H}}_{m}^{(0)}={\mathcal{B}}_{m}^{(0)}={\mathcal{J}}_{m}^{(0)}=0$
for all
![]() $m\geqslant 1$
, as the only order-1 term in the Bessel expansions is in
$m\geqslant 1$
, as the only order-1 term in the Bessel expansions is in
![]() $\text{J}_{0}$
. This yields a periodic unexcited solution to the damped Mathieu equation, which must be the zero solution.
$\text{J}_{0}$
. This yields a periodic unexcited solution to the damped Mathieu equation, which must be the zero solution.
To find
![]() $\unicode[STIX]{x1D6E4}_{W}$
, we first note that
$\unicode[STIX]{x1D6E4}_{W}$
, we first note that
![]() $a_{0}^{(0)}$
and
$a_{0}^{(0)}$
and
![]() $a_{1}^{(1)}$
are governed by inhomogeneities
$a_{1}^{(1)}$
are governed by inhomogeneities
Equating
![]() $\unicode[STIX]{x1D6FF}x$
from the walking condition (5.9), we require
$\unicode[STIX]{x1D6FF}x$
from the walking condition (5.9), we require
![]() $\unicode[STIX]{x1D6E4}_{W}$
such that
$\unicode[STIX]{x1D6E4}_{W}$
such that
Therefore, (5.16)–(5.18) is a closed system for
![]() $a_{0}^{(0)}$
,
$a_{0}^{(0)}$
,
![]() $a_{1}^{(1)}$
and
$a_{1}^{(1)}$
and
![]() $\unicode[STIX]{x1D6E4}_{W}$
. This nonlinear analysis gives a consistent walking threshold
$\unicode[STIX]{x1D6E4}_{W}$
. This nonlinear analysis gives a consistent walking threshold
![]() $\unicode[STIX]{x1D6E4}_{W}$
to the linear stability analysis in §§ 4.1 and 5.1.
$\unicode[STIX]{x1D6E4}_{W}$
to the linear stability analysis in §§ 4.1 and 5.1.
Given the solution to the above system, we may obtain equations for
![]() $\unicode[STIX]{x1D6E4}_{1}$
, which is coupled with equations for
$\unicode[STIX]{x1D6E4}_{1}$
, which is coupled with equations for
![]() $a_{0}^{(1)}$
and
$a_{0}^{(1)}$
and
![]() $a_{1}^{(2)}$
. By vanishing inhomogeneities,
$a_{1}^{(2)}$
. By vanishing inhomogeneities,
![]() $a_{2}^{(1)}\equiv 0$
, so
$a_{2}^{(1)}\equiv 0$
, so
The
![]() $\unicode[STIX]{x1D6FF}x^{2}$
term from (5.9) completes the system with
$\unicode[STIX]{x1D6FF}x^{2}$
term from (5.9) completes the system with
We now exploit the directional symmetry of the steady walker to show that
![]() $\unicode[STIX]{x1D6E4}_{1}=0$
. The map (5.1)–(5.2) also holds for
$\unicode[STIX]{x1D6E4}_{1}=0$
. The map (5.1)–(5.2) also holds for
![]() $\unicode[STIX]{x1D6FF}x<0$
, which corresponds to a droplet walking in the negative
$\unicode[STIX]{x1D6FF}x<0$
, which corresponds to a droplet walking in the negative
![]() $x$
-direction. Since
$x$
-direction. Since
![]() $a_{0}$
is the coefficient of the radially symmetric
$a_{0}$
is the coefficient of the radially symmetric
![]() $\text{J}_{0}(kr)$
basis function,
$\text{J}_{0}(kr)$
basis function,
![]() $a_{0}$
must be even in
$a_{0}$
must be even in
![]() $\unicode[STIX]{x1D6FF}x$
for the wave field to be the same for both walking directions. Hence, we require
$\unicode[STIX]{x1D6FF}x$
for the wave field to be the same for both walking directions. Hence, we require
![]() $a_{0}^{(1)}\equiv 0$
on
$a_{0}^{(1)}\equiv 0$
on
![]() $(0,1)$
. By (5.19), this is achieved if and only if
$(0,1)$
. By (5.19), this is achieved if and only if
![]() $\unicode[STIX]{x1D6E4}_{1}=0$
. With these vanishing terms, equation (5.20) becomes
$\unicode[STIX]{x1D6E4}_{1}=0$
. With these vanishing terms, equation (5.20) becomes
yielding
![]() $a_{1}^{(2)}\equiv 0$
on
$a_{1}^{(2)}\equiv 0$
on
![]() $(0,1)$
, which satisfies (5.21). Neglecting terms of
$(0,1)$
, which satisfies (5.21). Neglecting terms of
![]() $o(\unicode[STIX]{x1D6FF}x^{2})$
, we have
$o(\unicode[STIX]{x1D6FF}x^{2})$
, we have
which is valid for
![]() $0<\unicode[STIX]{x1D6FF}x\ll 1$
. Equations for determining
$0<\unicode[STIX]{x1D6FF}x\ll 1$
. Equations for determining
![]() $\unicode[STIX]{x1D6E4}_{2}>0$
are given in appendix C. The solution is shown in figure 1(a) (grey curve).
$\unicode[STIX]{x1D6E4}_{2}>0$
are given in appendix C. The solution is shown in figure 1(a) (grey curve).
5.3 Wave field of a single impact
Previous models for the wave field have superposed given radially symmetric sources centred at each impact with exponential temporal decay (Fort et al.
Reference Fort, Eddi, Boudaoud, Moukhtar and Couder2010; Eddi et al.
Reference Eddi, Sultan, Moukhtar, Fort, Rossi and Couder2011; Moláček & Bush Reference Moláček and Bush2013b
; Oza et al.
Reference Oza, Rosales and Bush2013). In our model, the jump conditions (3.25)–(3.26) at time
![]() $t_{n}$
are in fact equivalent to
$t_{n}$
are in fact equivalent to
![]() $[\unicode[STIX]{x1D702}(\boldsymbol{x},t_{n})]_{-}^{+}=\bar{\unicode[STIX]{x1D702}}(|\boldsymbol{x}-\boldsymbol{X}(t_{n})|,0)$
, where
$[\unicode[STIX]{x1D702}(\boldsymbol{x},t_{n})]_{-}^{+}=\bar{\unicode[STIX]{x1D702}}(|\boldsymbol{x}-\boldsymbol{X}(t_{n})|,0)$
, where
For all
![]() $k\geqslant 0$
,
$k\geqslant 0$
,
![]() $\bar{a}(t;k)$
is governed by
$\bar{a}(t;k)$
is governed by
![]() ${\mathcal{L}}_{k}\bar{a}=0$
for
${\mathcal{L}}_{k}\bar{a}=0$
for
![]() $t>0$
, with initial conditions
$t>0$
, with initial conditions
with
![]() $P_{0}(k)=kMG/(2\unicode[STIX]{x03C0})$
. This is quickly verified using Graf’s addition theorem (Abramowitz & Stegun Reference Abramowitz and Stegun1964). As
$P_{0}(k)=kMG/(2\unicode[STIX]{x03C0})$
. This is quickly verified using Graf’s addition theorem (Abramowitz & Stegun Reference Abramowitz and Stegun1964). As
![]() $\bar{\unicode[STIX]{x1D702}}(r,0)=0$
for all
$\bar{\unicode[STIX]{x1D702}}(r,0)=0$
for all
![]() $r$
, the wave field is continuous across the droplet impact, which is not true in the aforementioned models. Although
$r$
, the wave field is continuous across the droplet impact, which is not true in the aforementioned models. Although
![]() $\bar{\unicode[STIX]{x1D702}}_{t}(r,0)=\infty$
for all
$\bar{\unicode[STIX]{x1D702}}_{t}(r,0)=\infty$
for all
![]() $r\geqslant 0$
(from the
$r\geqslant 0$
(from the
![]() $\unicode[STIX]{x1D6FF}(\cdot )$
-function forcing), the rapid temporal decay of
$\unicode[STIX]{x1D6FF}(\cdot )$
-function forcing), the rapid temporal decay of
![]() $\bar{a}(t;k)$
for large
$\bar{a}(t;k)$
for large
![]() $k$
gives a finite solution for any
$k$
gives a finite solution for any
![]() $t>0$
. Furthermore,
$t>0$
. Furthermore,
![]() $\bar{\unicode[STIX]{x1D702}}$
depends only on the current position of the droplet and is independent of its velocity and path memory.
$\bar{\unicode[STIX]{x1D702}}$
depends only on the current position of the droplet and is independent of its velocity and path memory.
The development of this wave field over time is shown in figure 2(a). A decaying capillary wave propagates away from the droplet, which excites a field of standing Faraday waves. The wave field generated is similar to that of Milewski et al. (Reference Milewski, Galeano-Rios, Nachbin and Bush2015) near the origin, but differs slightly at the wave front over time. This dissimilarity may be explained partially by the assumption of instantaneous point impacts and the truncation of the wavenumbers. As the wave speed is much larger than the walking speed, this difference has a negligible effect on the resulting dynamics.

Figure 2. (a) The wave field of a single impact at times
![]() $1,\ldots ,8$
, which are normalised to have the same amplitude at the origin. A damped travelling capillary wave propagates from the impact, exciting a standing field of Faraday waves in its wake (
$1,\ldots ,8$
, which are normalised to have the same amplitude at the origin. A damped travelling capillary wave propagates from the impact, exciting a standing field of Faraday waves in its wake (
![]() $\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6E4}_{F}=0.994$
). (b) Spatial decay length
$\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6E4}_{F}=0.994$
). (b) Spatial decay length
![]() $l_{d}$
of a walker as a function of
$l_{d}$
of a walker as a function of
![]() $\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6E4}_{F}$
and memory
$\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6E4}_{F}$
and memory
![]() $M_{e}$
(inset (c)).
$M_{e}$
(inset (c)).
By superposition of such wave fields, we may now express the wave field
![]() $\unicode[STIX]{x1D702}$
by
$\unicode[STIX]{x1D702}$
by
where
![]() $H(\cdot )$
is the Heaviside function. Following Moláček & Bush (Reference Moláček and Bush2013b
), we define the dimensionless memory
$H(\cdot )$
is the Heaviside function. Following Moláček & Bush (Reference Moláček and Bush2013b
), we define the dimensionless memory
![]() $M_{e}(\unicode[STIX]{x1D6E4})$
, which is the number of impacts until
$M_{e}(\unicode[STIX]{x1D6E4})$
, which is the number of impacts until
![]() $\bar{\unicode[STIX]{x1D702}}$
becomes exponentially small. Using the calculations of Milewski et al. (Reference Milewski, Galeano-Rios, Nachbin and Bush2015), for
$\bar{\unicode[STIX]{x1D702}}$
becomes exponentially small. Using the calculations of Milewski et al. (Reference Milewski, Galeano-Rios, Nachbin and Bush2015), for
![]() $0<\unicode[STIX]{x1D6E4}_{F}-\unicode[STIX]{x1D6E4}\ll 1$
,
$0<\unicode[STIX]{x1D6E4}_{F}-\unicode[STIX]{x1D6E4}\ll 1$
,
is the dimensionless decay rate of the waves (
![]() $\unicode[STIX]{x1D6E4}_{F}=5.13$
for this fluid model). The critical wavenumber
$\unicode[STIX]{x1D6E4}_{F}=5.13$
for this fluid model). The critical wavenumber
![]() $k_{c}$
(
$k_{c}$
(
![]() $\unicode[STIX]{x1D6E4}$
) is the least-damped wavenumber given
$\unicode[STIX]{x1D6E4}$
) is the least-damped wavenumber given
![]() $\unicode[STIX]{x1D6E4}$
. This dependence is weak, with a 1 % variation in
$\unicode[STIX]{x1D6E4}$
. This dependence is weak, with a 1 % variation in
![]() $k_{c}(\unicode[STIX]{x1D6E4})$
away from
$k_{c}(\unicode[STIX]{x1D6E4})$
away from
![]() $k_{c}(\unicode[STIX]{x1D6E4}_{F})=k_{F}$
for a range of
$k_{c}(\unicode[STIX]{x1D6E4}_{F})=k_{F}$
for a range of
![]() $\unicode[STIX]{x1D6E4}$
, resulting in a small variation to
$\unicode[STIX]{x1D6E4}$
, resulting in a small variation to
![]() $T_{d}(\unicode[STIX]{x1D6E4})$
(typically
$T_{d}(\unicode[STIX]{x1D6E4})$
(typically
![]() $T_{d}(\unicode[STIX]{x1D6E4})\approx 0.6$
). This form is slightly more sophisticated than that of Moláček & Bush (Reference Moláček and Bush2013b
), where
$T_{d}(\unicode[STIX]{x1D6E4})\approx 0.6$
). This form is slightly more sophisticated than that of Moláček & Bush (Reference Moláček and Bush2013b
), where
![]() $T_{d}$
is assumed to be constant. From numerical verification, this is also a reasonable approximation for the range of
$T_{d}$
is assumed to be constant. From numerical verification, this is also a reasonable approximation for the range of
![]() $\unicode[STIX]{x1D6E4}$
considered.
$\unicode[STIX]{x1D6E4}$
considered.
From figure 2(a), the wave field approaches a Bessel-like function as time increases. As
![]() $k_{F}$
is the least-damped wavenumber,
$k_{F}$
is the least-damped wavenumber,
![]() $\bar{a}(t;k)$
is peaked about
$\bar{a}(t;k)$
is peaked about
![]() $k=k_{F}$
for large
$k=k_{F}$
for large
![]() $t$
. Hence, the integral for
$t$
. Hence, the integral for
![]() $\bar{\unicode[STIX]{x1D702}}(r,t)$
may be approximated by
$\bar{\unicode[STIX]{x1D702}}(r,t)$
may be approximated by
![]() $\bar{\unicode[STIX]{x1D702}}(r,t)=a_{0}(t;k_{F})\text{J}_{0}(k_{F}r)$
for large
$\bar{\unicode[STIX]{x1D702}}(r,t)=a_{0}(t;k_{F})\text{J}_{0}(k_{F}r)$
for large
![]() $t$
. The function
$t$
. The function
![]() $a_{0}(t;k_{F})$
has a Floquet exponent with real part
$a_{0}(t;k_{F})$
has a Floquet exponent with real part
![]() $-1/M_{e}$
, where the underlying periodic behaviour is well approximated by a sinusoid. This long-time approximation is used by Moláček & Bush (Reference Moláček and Bush2013b
) and Oza et al. (Reference Oza, Rosales and Bush2013), and prevents the occurrence of a travelling capillary wave formed at each impact and a Doppler shift. As our model generates a similar wave field to that of Milewski et al. (Reference Milewski, Galeano-Rios, Nachbin and Bush2015), we refer the reader to their paper for a comprehensive comparison between wave field models.
$-1/M_{e}$
, where the underlying periodic behaviour is well approximated by a sinusoid. This long-time approximation is used by Moláček & Bush (Reference Moláček and Bush2013b
) and Oza et al. (Reference Oza, Rosales and Bush2013), and prevents the occurrence of a travelling capillary wave formed at each impact and a Doppler shift. As our model generates a similar wave field to that of Milewski et al. (Reference Milewski, Galeano-Rios, Nachbin and Bush2015), we refer the reader to their paper for a comprehensive comparison between wave field models.
The wavenumbers near to
![]() $k_{F}$
also prove to be significant in leading to the experimentally observed spatial damping (Eddi et al.
Reference Eddi, Sultan, Moukhtar, Fort, Rossi and Couder2011), and are computed numerically Milewski et al. (Reference Milewski, Galeano-Rios, Nachbin and Bush2015). We repeat their statistical calculation for our model, with the resulting exponential decay length
$k_{F}$
also prove to be significant in leading to the experimentally observed spatial damping (Eddi et al.
Reference Eddi, Sultan, Moukhtar, Fort, Rossi and Couder2011), and are computed numerically Milewski et al. (Reference Milewski, Galeano-Rios, Nachbin and Bush2015). We repeat their statistical calculation for our model, with the resulting exponential decay length
![]() $l_{d}$
shown in figure 2(b). Specifically, we compute the wave field
$l_{d}$
shown in figure 2(b). Specifically, we compute the wave field
![]() $\unicode[STIX]{x1D702}$
for a walker, and find the extrema to
$\unicode[STIX]{x1D702}$
for a walker, and find the extrema to
![]() $|\unicode[STIX]{x1D702}|$
in the direction perpendicular to travel. As the far-field spatial decay of a Bessel function is
$|\unicode[STIX]{x1D702}|$
in the direction perpendicular to travel. As the far-field spatial decay of a Bessel function is
![]() ${\sim}1/\sqrt{r}$
, we fit a nonlinear model of the form
${\sim}1/\sqrt{r}$
, we fit a nonlinear model of the form
![]() $\unicode[STIX]{x1D703}_{1}\exp (-r/\unicode[STIX]{x1D703}_{2})/\sqrt{r}$
for parameters
$\unicode[STIX]{x1D703}_{1}\exp (-r/\unicode[STIX]{x1D703}_{2})/\sqrt{r}$
for parameters
![]() $(\unicode[STIX]{x1D703}_{1},\unicode[STIX]{x1D703}_{2})$
, where
$(\unicode[STIX]{x1D703}_{1},\unicode[STIX]{x1D703}_{2})$
, where
![]() $l_{d}=\unicode[STIX]{x1D703}_{2}$
, which is an approximate envelope for the wave field. Typically, we consider
$l_{d}=\unicode[STIX]{x1D703}_{2}$
, which is an approximate envelope for the wave field. Typically, we consider
![]() $r\in (0,10]$
, which gives enough points for a reasonable statistical fit. As this approach contains some numerical error, the resulting solution is not smooth.
$r\in (0,10]$
, which gives enough points for a reasonable statistical fit. As this approach contains some numerical error, the resulting solution is not smooth.
The spatial decay length
![]() $l_{d}$
increases with
$l_{d}$
increases with
![]() $\unicode[STIX]{x1D6E4}$
, and grows linearly with memory as
$\unicode[STIX]{x1D6E4}$
, and grows linearly with memory as
![]() $M_{e}\rightarrow \infty$
. However, due to the fixed impact phase, we do not obtain jumps in the decay length as the impacts switch between
$M_{e}\rightarrow \infty$
. However, due to the fixed impact phase, we do not obtain jumps in the decay length as the impacts switch between
![]() $(m,n)$
modes (Milewski et al.
Reference Milewski, Galeano-Rios, Nachbin and Bush2015). As Eddi et al. (Reference Eddi, Sultan, Moukhtar, Fort, Rossi and Couder2011) and Borghesi et al. (Reference Borghesi, Moukhtar, Labousse, Eddi, Fort and Couder2014) used fixed dimensionless values of
$(m,n)$
modes (Milewski et al.
Reference Milewski, Galeano-Rios, Nachbin and Bush2015). As Eddi et al. (Reference Eddi, Sultan, Moukhtar, Fort, Rossi and Couder2011) and Borghesi et al. (Reference Borghesi, Moukhtar, Labousse, Eddi, Fort and Couder2014) used fixed dimensionless values of
![]() $l_{d}=1.6$
and
$l_{d}=1.6$
and
![]() $2.5$
respectively, they did not capture this intrinsic change in the wave field as
$2.5$
respectively, they did not capture this intrinsic change in the wave field as
![]() $\unicode[STIX]{x1D6E4}$
varies.
$\unicode[STIX]{x1D6E4}$
varies.
5.4 Doppler effect
As shown by Eddi et al. (Reference Eddi, Sultan, Moukhtar, Fort, Rossi and Couder2011), a Doppler effect is observed in the wave field of the walker; the waves ahead of the droplet are compressed, yet are elongated behind. This phenomenon was observed in the simulations of Milewski et al. (Reference Milewski, Galeano-Rios, Nachbin and Bush2015). Moreover, the authors proved that this cannot occur for wave amplitudes of the form
![]() $a(t;k)=\unicode[STIX]{x1D6FC}(t)\unicode[STIX]{x1D6FF}(k-k_{F})$
, which was used in Oza et al. (Reference Oza, Rosales and Bush2013). However, as we maintain a significant range of
$a(t;k)=\unicode[STIX]{x1D6FC}(t)\unicode[STIX]{x1D6FF}(k-k_{F})$
, which was used in Oza et al. (Reference Oza, Rosales and Bush2013). However, as we maintain a significant range of
![]() $k$
in our numerical solution, we observe a Doppler effect far from the droplet (figure 3). Our model exhibits a smooth yet nonlinear change in the wavelength due to the Doppler effect, which differs from the linear prediction of Eddi et al. (Reference Eddi, Sultan, Moukhtar, Fort, Rossi and Couder2011).
$k$
in our numerical solution, we observe a Doppler effect far from the droplet (figure 3). Our model exhibits a smooth yet nonlinear change in the wavelength due to the Doppler effect, which differs from the linear prediction of Eddi et al. (Reference Eddi, Sultan, Moukhtar, Fort, Rossi and Couder2011).

Figure 3. Evidence of a Doppler effect. (a) Wave in direction of travel (black) and transverse wave (grey) recentred to have the same peaks. The arrow determines the direction of travel, where
![]() $\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6E4}_{F}=0.9$
. Waves are elongated behind the droplet and compressed ahead. (b) Measured wavelengths behind
$\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6E4}_{F}=0.9$
. Waves are elongated behind the droplet and compressed ahead. (b) Measured wavelengths behind
![]() $(+)$
and ahead
$(+)$
and ahead
![]() $(\times )$
of the droplet. The grey lines are the theoretical predictions made by Eddi et al. (Reference Eddi, Sultan, Moukhtar, Fort, Rossi and Couder2011).
$(\times )$
of the droplet. The grey lines are the theoretical predictions made by Eddi et al. (Reference Eddi, Sultan, Moukhtar, Fort, Rossi and Couder2011).

Figure 4. Wave fields corresponding to different steady-state dynamics at droplet impact. The droplet is denoted by a blue circle for in-phase impacts and a red circle when in flight for antiphase dynamics. Walking droplets for (a)
![]() $\unicode[STIX]{x1D6FF}x=0.065$
with
$\unicode[STIX]{x1D6FF}x=0.065$
with
![]() $\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6E4}_{F}=0.9$
and (b)
$\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6E4}_{F}=0.9$
and (b)
![]() $\unicode[STIX]{x1D6FF}x=0.08$
with
$\unicode[STIX]{x1D6FF}x=0.08$
with
![]() $\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6E4}_{F}=0.96$
. Two anticlockwise orbiting droplets with
$\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6E4}_{F}=0.96$
. Two anticlockwise orbiting droplets with
![]() $\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6E4}_{F}=0.91$
for (c) in-phase and (d) antiphase impacts. A single droplet orbiting anticlockwise under a central force for
$\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6E4}_{F}=0.91$
for (c) in-phase and (d) antiphase impacts. A single droplet orbiting anticlockwise under a central force for
![]() $\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6E4}_{F}=0.975$
with orbit radius (e)
$\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6E4}_{F}=0.975$
with orbit radius (e)
![]() $R_{d}=0.45$
and (f)
$R_{d}=0.45$
and (f)
![]() $R_{d}=0.95$
.
$R_{d}=0.95$
.
5.5 Summary of steady walking dynamics
To conclude this section, a bouncing droplet destabilises via a pitchfork bifurcation to a steady walker, whose lower-energy wave field automatically captures the exponential spatial damping correction observed in experiments (Eddi et al.
Reference Eddi, Sultan, Moukhtar, Fort, Rossi and Couder2011). The jump conditions are equivalent to adding a radially symmetric propagating wave field
![]() $\bar{\unicode[STIX]{x1D702}}$
at each impact, whose temporal equidistant superposition yields a Doppler shift, with a weakly nonlinear dependence on
$\bar{\unicode[STIX]{x1D702}}$
at each impact, whose temporal equidistant superposition yields a Doppler shift, with a weakly nonlinear dependence on
![]() $\unicode[STIX]{x1D6FF}x$
. Furthermore, the temporal decay of the system may be described by its memory
$\unicode[STIX]{x1D6FF}x$
. Furthermore, the temporal decay of the system may be described by its memory
![]() $M_{e}(\unicode[STIX]{x1D6E4})$
, which allows for comparison between previous models (Fort et al.
Reference Fort, Eddi, Boudaoud, Moukhtar and Couder2010; Moláček & Bush Reference Moláček and Bush2013b
). The wave fields corresponding to the dynamics of a walker are easily computed and are shown in figures 4(a) and 4(b) for two different walking speeds. For large
$M_{e}(\unicode[STIX]{x1D6E4})$
, which allows for comparison between previous models (Fort et al.
Reference Fort, Eddi, Boudaoud, Moukhtar and Couder2010; Moláček & Bush Reference Moláček and Bush2013b
). The wave fields corresponding to the dynamics of a walker are easily computed and are shown in figures 4(a) and 4(b) for two different walking speeds. For large
![]() $\unicode[STIX]{x1D6E4}$
, an interference pattern forms behind the droplet (Eddi et al.
Reference Eddi, Sultan, Moukhtar, Fort, Rossi and Couder2011).
$\unicode[STIX]{x1D6E4}$
, an interference pattern forms behind the droplet (Eddi et al.
Reference Eddi, Sultan, Moukhtar, Fort, Rossi and Couder2011).
6 Multiple-droplet interactions
In this section, we analyse three experimentally observed configurations for multiple droplets: orbiting pairs, side-by-side walkers (promenades) and trains of walkers. For
![]() $N$
droplets
$N$
droplets
![]() $\boldsymbol{X}^{(1)}(t),\ldots ,\boldsymbol{X}^{(N)}(t)$
, each droplet is governed by (3.24) during flight (with
$\boldsymbol{X}^{(1)}(t),\ldots ,\boldsymbol{X}^{(N)}(t)$
, each droplet is governed by (3.24) during flight (with
![]() $\tilde{\unicode[STIX]{x1D705}}=0$
) and the jump condition (3.27) at impact. The wave amplitudes are still modelled by the damped Mathieu equations (3.22)–(3.23) during flight, but for in-phase interactions, the jump condition (3.25) becomes
$\tilde{\unicode[STIX]{x1D705}}=0$
) and the jump condition (3.27) at impact. The wave amplitudes are still modelled by the damped Mathieu equations (3.22)–(3.23) during flight, but for in-phase interactions, the jump condition (3.25) becomes
and similarly for
![]() $b_{m}^{\prime }$
. For antiphase impacts, additional jumps occur at
$b_{m}^{\prime }$
. For antiphase impacts, additional jumps occur at
![]() $t=t_{n+1/2}\equiv t_{n}+1/2$
. In the bifurcation diagrams that follow in §§ 6 and 7, we identify three stability types, as described in table 2. A pair of unstable complex conjugate (c.c.) eigenvalues often allows the system to destabilise slowly to a new oscillatory stable regime.
$t=t_{n+1/2}\equiv t_{n}+1/2$
. In the bifurcation diagrams that follow in §§ 6 and 7, we identify three stability types, as described in table 2. A pair of unstable complex conjugate (c.c.) eigenvalues often allows the system to destabilise slowly to a new oscillatory stable regime.
Table 2. Stability types of the stability transition matrix
![]() $\unicode[STIX]{x1D64F}$
with complex eigenvalue spectrum
$\unicode[STIX]{x1D64F}$
with complex eigenvalue spectrum
![]() $\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D64F})$
. We define the set of unstable eigenvalues
$\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D64F})$
. We define the set of unstable eigenvalues
![]() ${\mathcal{U}}=\{\unicode[STIX]{x1D707}:\,\unicode[STIX]{x1D707}\in \unicode[STIX]{x1D70E}(\unicode[STIX]{x1D64F}),\,\,|\unicode[STIX]{x1D707}|>1\}$
, where
${\mathcal{U}}=\{\unicode[STIX]{x1D707}:\,\unicode[STIX]{x1D707}\in \unicode[STIX]{x1D70E}(\unicode[STIX]{x1D64F}),\,\,|\unicode[STIX]{x1D707}|>1\}$
, where
![]() ${\mathcal{U}}$
is empty only when the system is stable.
${\mathcal{U}}$
is empty only when the system is stable.

6.1 In-phase orbiting
We consider two orbiting droplets about the origin; both droplets impact simultaneously on a radius
![]() $R_{d}$
, with the droplets and wave field rotating by an angle
$R_{d}$
, with the droplets and wave field rotating by an angle
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703}>0$
between impacts. Moreover, we pose that the angular difference between
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703}>0$
between impacts. Moreover, we pose that the angular difference between
![]() $\boldsymbol{X}^{(1)}(t_{n})$
and
$\boldsymbol{X}^{(1)}(t_{n})$
and
![]() $\boldsymbol{X}^{(2)}(t_{n})$
is
$\boldsymbol{X}^{(2)}(t_{n})$
is
![]() $\unicode[STIX]{x03C0}$
for all
$\unicode[STIX]{x03C0}$
for all
![]() $t_{n}$
. This allows us to model
$t_{n}$
. This allows us to model
![]() $\boldsymbol{X}^{(1)}(t)$
explicitly, with the contribution of
$\boldsymbol{X}^{(1)}(t)$
explicitly, with the contribution of
![]() $\boldsymbol{X}^{(2)}(t_{n})$
to the wave amplitude jump conditions treated implicitly. For notational convenience, we write
$\boldsymbol{X}^{(2)}(t_{n})$
to the wave amplitude jump conditions treated implicitly. For notational convenience, we write
![]() $\boldsymbol{X}(t)\equiv \boldsymbol{X}^{(1)}(t)$
, where
$\boldsymbol{X}(t)\equiv \boldsymbol{X}^{(1)}(t)$
, where
![]() $\boldsymbol{X}(t_{n})$
has radial component
$\boldsymbol{X}(t_{n})$
has radial component
![]() $r_{d}(t_{n})=R_{d}$
and angular component
$r_{d}(t_{n})=R_{d}$
and angular component
![]() $\unicode[STIX]{x1D703}_{d}(t_{n})=\unicode[STIX]{x1D703}_{n}\equiv n\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703}$
(by rotational invariance). The droplet motion is piecewise linear, so
$\unicode[STIX]{x1D703}_{d}(t_{n})=\unicode[STIX]{x1D703}_{n}\equiv n\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703}$
(by rotational invariance). The droplet motion is piecewise linear, so
![]() $r_{d}(t)\neq R_{d}$
for
$r_{d}(t)\neq R_{d}$
for
![]() $t\neq t_{n}$
.
$t\neq t_{n}$
.
As the implicit second droplet has angular component
![]() $(\unicode[STIX]{x1D703}_{n}+\unicode[STIX]{x03C0})$
at time
$(\unicode[STIX]{x1D703}_{n}+\unicode[STIX]{x03C0})$
at time
![]() $t_{n}$
, (6.1) gives
$t_{n}$
, (6.1) gives
For
![]() $m$
odd,
$m$
odd,
![]() $a_{m}$
and
$a_{m}$
and
![]() $b_{m}$
are never excited during the orbit, giving
$b_{m}$
are never excited during the orbit, giving
![]() $a_{m}\equiv b_{m}\equiv 0$
. This ensures that the wave field with respect to each droplet is the same.
$a_{m}\equiv b_{m}\equiv 0$
. This ensures that the wave field with respect to each droplet is the same.
Denoting
![]() $\boldsymbol{c}_{m}(t;k)=(a_{m}(t;k),b_{m}(t;k))^{\text{T}}$
, the wave field rotates with the droplets if
$\boldsymbol{c}_{m}(t;k)=(a_{m}(t;k),b_{m}(t;k))^{\text{T}}$
, the wave field rotates with the droplets if
where
![]() $\unicode[STIX]{x1D63F}(\unicode[STIX]{x1D711})\in \mathbb{R}^{2\times 2}$
is the rotation matrix for angle
$\unicode[STIX]{x1D63F}(\unicode[STIX]{x1D711})\in \mathbb{R}^{2\times 2}$
is the rotation matrix for angle
![]() $\unicode[STIX]{x1D711}$
. The droplet rotation requires
$\unicode[STIX]{x1D711}$
. The droplet rotation requires
As with steady walking, we solve the droplet dynamics (3.24)–(3.27) with
![]() $\tilde{\unicode[STIX]{x1D705}}=0$
for
$\tilde{\unicode[STIX]{x1D705}}=0$
for
![]() $t\in [t_{n},t_{n+1})$
subject to (6.5), and eliminate
$t\in [t_{n},t_{n+1})$
subject to (6.5), and eliminate
![]() $\boldsymbol{X}^{\prime }(t_{n}^{+})$
in favour of
$\boldsymbol{X}^{\prime }(t_{n}^{+})$
in favour of
![]() $\boldsymbol{X}(t_{n})$
. This gives
$\boldsymbol{X}(t_{n})$
. This gives
where
![]() $(\unicode[STIX]{x1D735}\unicode[STIX]{x1D702})_{n}\equiv \unicode[STIX]{x1D735}\unicode[STIX]{x1D702}(\boldsymbol{X}(t_{n}),t_{n})$
, and
$(\unicode[STIX]{x1D735}\unicode[STIX]{x1D702})_{n}\equiv \unicode[STIX]{x1D735}\unicode[STIX]{x1D702}(\boldsymbol{X}(t_{n}),t_{n})$
, and
![]() $(\unicode[STIX]{x1D735}\unicode[STIX]{x1D702})_{n+1}=\unicode[STIX]{x1D63F}(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703})(\unicode[STIX]{x1D735}\unicode[STIX]{x1D702})_{n}$
due to the rotation.
$(\unicode[STIX]{x1D735}\unicode[STIX]{x1D702})_{n+1}=\unicode[STIX]{x1D63F}(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703})(\unicode[STIX]{x1D735}\unicode[STIX]{x1D702})_{n}$
due to the rotation.
We need to find
![]() $R_{d}$
and
$R_{d}$
and
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703}$
such that the wave field amplitudes governed by (3.22)–(3.23) with jump conditions (6.2)–(6.3) satisfy the rotation conditions (6.4) and droplet condition (6.6). By periodicity, it is sufficient to solve for
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703}$
such that the wave field amplitudes governed by (3.22)–(3.23) with jump conditions (6.2)–(6.3) satisfy the rotation conditions (6.4) and droplet condition (6.6). By periodicity, it is sufficient to solve for
![]() $n=0$
(so
$n=0$
(so
![]() $t\in [0,1]$
), where
$t\in [0,1]$
), where
![]() $\boldsymbol{X}(t_{0})=(R_{d},0)^{\text{T}}$
. This is formulated as many
$\boldsymbol{X}(t_{0})=(R_{d},0)^{\text{T}}$
. This is formulated as many
![]() $4\times 4$
linear systems subject to (6.6), akin to finding the walking states. An example in-phase wave field is given in figure 4(
$4\times 4$
linear systems subject to (6.6), akin to finding the walking states. An example in-phase wave field is given in figure 4(
![]() $c$
).
$c$
).
The stability analysis is similar to that of the walking states with two independent droplet perturbations, although we rotate the domain by
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703}$
between iterations so that the steady-state droplet always lies at
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703}$
between iterations so that the steady-state droplet always lies at
![]() $(r,\unicode[STIX]{x1D703})=(R_{d},0)$
in the current domain. It should be noted that the wave amplitudes
$(r,\unicode[STIX]{x1D703})=(R_{d},0)$
in the current domain. It should be noted that the wave amplitudes
![]() $a_{m}$
and
$a_{m}$
and
![]() $b_{m}$
are required for all
$b_{m}$
are required for all
![]() $m$
(not just even indices), and the system is truncated for sufficiently large
$m$
(not just even indices), and the system is truncated for sufficiently large
![]() $m$
given
$m$
given
![]() $R_{d}$
, by the shape of the large-order Bessel functions near zero (it should be recalled that
$R_{d}$
, by the shape of the large-order Bessel functions near zero (it should be recalled that
![]() $\text{J}_{m}(z)\sim (1/m!)(z/2)^{m}$
for
$\text{J}_{m}(z)\sim (1/m!)(z/2)^{m}$
for
![]() $0<z\ll \sqrt{m+1}$
).
$0<z\ll \sqrt{m+1}$
).

Figure 5. (a) Bifurcation diagram for the diameters
![]() $D$
of in-phase
$D$
of in-phase
![]() $I_{n}$
(light grey background) and antiphase
$I_{n}$
(light grey background) and antiphase
![]() $A_{n}$
(white background) orbiting pairs. The dark grey regions give the bounds for two droplets in a stable wobbly orbit. This has an upper bound given by the unstable upper branch. The curves correspond to stability types in table 2. (b) Example wobbly in-phase anticlockwise orbiters with
$A_{n}$
(white background) orbiting pairs. The dark grey regions give the bounds for two droplets in a stable wobbly orbit. This has an upper bound given by the unstable upper branch. The curves correspond to stability types in table 2. (b) Example wobbly in-phase anticlockwise orbiters with
![]() $\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6E4}_{F}=0.83$
, which corresponds to the black cross in (a).
$\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6E4}_{F}=0.83$
, which corresponds to the black cross in (a).
The orbit diameters
![]() $D\equiv 2R_{d}$
are shown in figure 5(a), where curves with a light grey background correspond to in-phase orbiters. The diameters of the stable solutions are in good agreement with the experimental values recorded by Couder et al. (Reference Couder, Protière, Fort and Boudaoud2005b
), namely
$D\equiv 2R_{d}$
are shown in figure 5(a), where curves with a light grey background correspond to in-phase orbiters. The diameters of the stable solutions are in good agreement with the experimental values recorded by Couder et al. (Reference Couder, Protière, Fort and Boudaoud2005b
), namely
![]() $D_{n}=(n-\bar{\unicode[STIX]{x1D716}})$
, where
$D_{n}=(n-\bar{\unicode[STIX]{x1D716}})$
, where
![]() $\bar{\unicode[STIX]{x1D716}}\approx 0.2$
and
$\bar{\unicode[STIX]{x1D716}}\approx 0.2$
and
![]() $n$
is an integer. However, the co-existence of stable
$n$
is an integer. However, the co-existence of stable
![]() $n=1,2,3$
orbits occurs only for a limited range of
$n=1,2,3$
orbits occurs only for a limited range of
![]() $\unicode[STIX]{x1D6E4}$
. This system also contains wobbly orbits, which appear when the steady orbit destabilises via a complex conjugate pair of eigenvalues. Due to nonlinear effects, the droplets remain locked in a periodic wobbly orbit (see figure 5(b)). The minimum and maximum distances apart reached by the droplets are indicated by the dark grey regions in figure 5(a), and are obtained by simulating away from the steady states. We observe that the maximum distance apart is bounded above by the corresponding unstable upper branch to each solution, which sheds some light on why wobbly solutions only exist over a limited range of
$\unicode[STIX]{x1D6E4}$
. This system also contains wobbly orbits, which appear when the steady orbit destabilises via a complex conjugate pair of eigenvalues. Due to nonlinear effects, the droplets remain locked in a periodic wobbly orbit (see figure 5(b)). The minimum and maximum distances apart reached by the droplets are indicated by the dark grey regions in figure 5(a), and are obtained by simulating away from the steady states. We observe that the maximum distance apart is bounded above by the corresponding unstable upper branch to each solution, which sheds some light on why wobbly solutions only exist over a limited range of
![]() $\unicode[STIX]{x1D6E4}$
.
$\unicode[STIX]{x1D6E4}$
.
For further insight, we consider the solution at
![]() $\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E4}_{F}$
with wavenumber
$\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E4}_{F}$
with wavenumber
![]() $k=k_{F}$
. The Floquet exponents are
$k=k_{F}$
. The Floquet exponents are
![]() $\unicode[STIX]{x1D707}_{1}=0$
and
$\unicode[STIX]{x1D707}_{1}=0$
and
![]() $\unicode[STIX]{x1D707}_{2}=-2\unicode[STIX]{x1D6FE}(k_{F})$
, giving the eigenvalues of the Mathieu fundamental matrix
$\unicode[STIX]{x1D707}_{2}=-2\unicode[STIX]{x1D6FE}(k_{F})$
, giving the eigenvalues of the Mathieu fundamental matrix
![]() $\unicode[STIX]{x1D648}_{k_{F}}(\unicode[STIX]{x1D6E4}_{F})$
as
$\unicode[STIX]{x1D648}_{k_{F}}(\unicode[STIX]{x1D6E4}_{F})$
as
![]() $\unicode[STIX]{x1D70C}_{1}\equiv \exp (\unicode[STIX]{x1D707}_{1})=1$
and
$\unicode[STIX]{x1D70C}_{1}\equiv \exp (\unicode[STIX]{x1D707}_{1})=1$
and
![]() $\unicode[STIX]{x1D70C}_{2}\equiv \exp (\unicode[STIX]{x1D707}_{2})$
. Periodicity requires
$\unicode[STIX]{x1D70C}_{2}\equiv \exp (\unicode[STIX]{x1D707}_{2})$
. Periodicity requires
where
![]() $(\unicode[STIX]{x1D644}_{2}-\unicode[STIX]{x1D648}_{k_{F}}(\unicode[STIX]{x1D6E4}_{F}))$
is singular. A candidate radius
$(\unicode[STIX]{x1D644}_{2}-\unicode[STIX]{x1D648}_{k_{F}}(\unicode[STIX]{x1D6E4}_{F}))$
is singular. A candidate radius
![]() $R_{d}$
satisfies
$R_{d}$
satisfies
![]() $\text{J}_{0}(k_{F}R_{d})=0$
, with a corresponding wave amplitude vector from the matrix null space. In fact, such radii satisfy the full problem and correspond to the lower branches in figure 5(a) as
$\text{J}_{0}(k_{F}R_{d})=0$
, with a corresponding wave amplitude vector from the matrix null space. In fact, such radii satisfy the full problem and correspond to the lower branches in figure 5(a) as
![]() $\unicode[STIX]{x1D6E4}\rightarrow \unicode[STIX]{x1D6E4}_{F}$
.
$\unicode[STIX]{x1D6E4}\rightarrow \unicode[STIX]{x1D6E4}_{F}$
.
6.2 Antiphase orbiting
For antiphase orbiting of two droplets, we impose that
![]() $\boldsymbol{X}^{(1)}(t_{n})$
and
$\boldsymbol{X}^{(1)}(t_{n})$
and
![]() $\boldsymbol{X}^{(2)}(t_{n+1/2})$
both lie on the radius
$\boldsymbol{X}^{(2)}(t_{n+1/2})$
both lie on the radius
![]() $R_{d}$
with angular components
$R_{d}$
with angular components
![]() $\unicode[STIX]{x1D703}_{n}$
and
$\unicode[STIX]{x1D703}_{n}$
and
![]() $(\unicode[STIX]{x1D703}_{n+1/2}+\unicode[STIX]{x03C0})$
respectively, where
$(\unicode[STIX]{x1D703}_{n+1/2}+\unicode[STIX]{x03C0})$
respectively, where
![]() $t_{n+1/2}\equiv t_{n}+1/2$
and
$t_{n+1/2}\equiv t_{n}+1/2$
and
![]() $\unicode[STIX]{x1D703}_{n+1/2}\equiv \unicode[STIX]{x1D703}_{n}+\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703}/2.$
We construct the wave field to rotate by
$\unicode[STIX]{x1D703}_{n+1/2}\equiv \unicode[STIX]{x1D703}_{n}+\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703}/2.$
We construct the wave field to rotate by
![]() $\unicode[STIX]{x03C0}+\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703}/2$
in half of an impact period, which ensures that the wave field is the same with respect to each droplet at impact. The antiphase jump conditions are
$\unicode[STIX]{x03C0}+\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703}/2$
in half of an impact period, which ensures that the wave field is the same with respect to each droplet at impact. The antiphase jump conditions are
Hence, both odd and even
![]() $m$
are required for antiphase orbiters.
$m$
are required for antiphase orbiters.
It remains to find
![]() $R_{d}$
and
$R_{d}$
and
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703}$
such that (6.6) is satisfied. This is coupled with Mathieu equations (3.22)–(3.23), jump conditions (6.8)–(6.9) and wave amplitude maps (6.4), but with
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703}$
such that (6.6) is satisfied. This is coupled with Mathieu equations (3.22)–(3.23), jump conditions (6.8)–(6.9) and wave amplitude maps (6.4), but with
![]() $t_{n+1}\mapsto t_{n+1/2}$
and
$t_{n+1}\mapsto t_{n+1/2}$
and
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703}\mapsto \unicode[STIX]{x03C0}+\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703}/2$
. An example wave field is shown in figure 4(
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703}\mapsto \unicode[STIX]{x03C0}+\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703}/2$
. An example wave field is shown in figure 4(
![]() $d$
). The stability analysis requires a two-stage transition map to account for the antiphase impacts.
$d$
). The stability analysis requires a two-stage transition map to account for the antiphase impacts.
The quantisation of antiphase orbiters is given by the regions of white background shown in figure 5(a). Although the reported orbit quantisation
![]() $D_{n}^{\prime }=(n+1/2-\bar{\unicode[STIX]{x1D716}})$
is obtained (Couder et al.
Reference Couder, Protière, Fort and Boudaoud2005b
), the range of stable solutions with
$D_{n}^{\prime }=(n+1/2-\bar{\unicode[STIX]{x1D716}})$
is obtained (Couder et al.
Reference Couder, Protière, Fort and Boudaoud2005b
), the range of stable solutions with
![]() $\unicode[STIX]{x1D6E4}$
is limited, particularly for the smallest orbit. We note that the stability and existence of solutions are dependent on the skidding friction
$\unicode[STIX]{x1D6E4}$
is limited, particularly for the smallest orbit. We note that the stability and existence of solutions are dependent on the skidding friction
![]() $c$
and impact phase
$c$
and impact phase
![]() $\unicode[STIX]{x1D6FD}$
, which are both fixed for this theoretical investigation. We expect that these results will be particularly sensitive to the impact phase.
$\unicode[STIX]{x1D6FD}$
, which are both fixed for this theoretical investigation. We expect that these results will be particularly sensitive to the impact phase.
6.3 Promenade pairs
For simplicity, we only analyse rectilinear promenade pairs. To exploit the symmetry of two in-phase droplets, we fix the droplets to walk in parallel along lines
![]() $y=\pm \unicode[STIX]{x1D6FF}y$
in the direction of increasing
$y=\pm \unicode[STIX]{x1D6FF}y$
in the direction of increasing
![]() $x$
. To find
$x$
. To find
![]() $\unicode[STIX]{x1D6FF}y$
, we require
$\unicode[STIX]{x1D6FF}y$
, we require
![]() $\unicode[STIX]{x2202}_{y}\unicode[STIX]{x1D702}=0$
at each drop, and the walking speed
$\unicode[STIX]{x2202}_{y}\unicode[STIX]{x1D702}=0$
at each drop, and the walking speed
![]() $\unicode[STIX]{x1D6FF}x$
is given by an equation analogous to (5.9). This couples with the wave amplitude maps (5.3)–(5.4) and multiple-droplet jump conditions (6.1), with
$\unicode[STIX]{x1D6FF}x$
is given by an equation analogous to (5.9). This couples with the wave amplitude maps (5.3)–(5.4) and multiple-droplet jump conditions (6.1), with
![]() $\boldsymbol{X}^{(1)}(t_{n})=(n\unicode[STIX]{x1D6FF}x,\unicode[STIX]{x1D6FF}y)$
and
$\boldsymbol{X}^{(1)}(t_{n})=(n\unicode[STIX]{x1D6FF}x,\unicode[STIX]{x1D6FF}y)$
and
![]() $\boldsymbol{X}^{(2)}(t_{n})=(n\unicode[STIX]{x1D6FF}x,-\unicode[STIX]{x1D6FF}y)$
. The stability analysis follows similarly to the walking case, yet the two droplets have independent perturbations.
$\boldsymbol{X}^{(2)}(t_{n})=(n\unicode[STIX]{x1D6FF}x,-\unicode[STIX]{x1D6FF}y)$
. The stability analysis follows similarly to the walking case, yet the two droplets have independent perturbations.

Figure 6. Bifurcation diagram for (a) promenade pairs and (b) two-droplet trains as a function of distance apart
![]() $D$
and speed relative to a single walker
$D$
and speed relative to a single walker
![]() $\unicode[STIX]{x1D6FF}x/\unicode[STIX]{x1D6FF}x_{1}$
. Grey and white backgrounds denote in-phase and antiphase dynamics respectively. The thin grey lines connect points of equal
$\unicode[STIX]{x1D6FF}x/\unicode[STIX]{x1D6FF}x_{1}$
. Grey and white backgrounds denote in-phase and antiphase dynamics respectively. The thin grey lines connect points of equal
![]() $\tilde{\unicode[STIX]{x1D6E4}}\equiv \unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6E4}_{F}$
. The thick lines correspond to stability types in table 2.
$\tilde{\unicode[STIX]{x1D6E4}}\equiv \unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6E4}_{F}$
. The thick lines correspond to stability types in table 2.
The extension to antiphase promenaders is analogous to that for orbiters. In half of an impact period, we require the wave field to be translated
![]() $\unicode[STIX]{x1D6FF}x/2$
along the
$\unicode[STIX]{x1D6FF}x/2$
along the
![]() $x$
-axis and reflected about
$x$
-axis and reflected about
![]() $y=0$
. This ensures that each droplet receives the same kick at impact.
$y=0$
. This ensures that each droplet receives the same kick at impact.
Results are shown in figure 6(a), where the grey and white backgrounds correspond to in-phase and antiphase dynamics, respectively. We first observe that the speed of a promenading pair is less than that of a single walker, as reported by Borghesi et al. (Reference Borghesi, Moukhtar, Labousse, Eddi, Fort and Couder2014). The quantised distance between droplets
![]() $D\equiv 2\unicode[STIX]{x1D6FF}y$
depends weakly on
$D\equiv 2\unicode[STIX]{x1D6FF}y$
depends weakly on
![]() $\unicode[STIX]{x1D6E4}$
, which was not reported in Borghesi et al. (Reference Borghesi, Moukhtar, Labousse, Eddi, Fort and Couder2014). Instead, the authors stated that
$\unicode[STIX]{x1D6E4}$
, which was not reported in Borghesi et al. (Reference Borghesi, Moukhtar, Labousse, Eddi, Fort and Couder2014). Instead, the authors stated that
![]() $D$
has approximate in-phase values of
$D$
has approximate in-phase values of
![]() $0.6,1.6,2.6,\ldots$
and antiphase values of
$0.6,1.6,2.6,\ldots$
and antiphase values of
![]() $1.1,2.1,3.1,\ldots$
, which is consistent with our findings.
$1.1,2.1,3.1,\ldots$
, which is consistent with our findings.
Crucially, we note that straight-line promenade pairs are unstable for all quantisations and all values of
![]() $\unicode[STIX]{x1D6E4}$
. When there is an oscillatory instability (with no real eigenvalue), we expect the droplets to become bound in parallel motion, but with a transverse oscillation, as reported in experiments (Protière et al.
Reference Protière, Boudaoud and Couder2006; Borghesi et al.
Reference Borghesi, Moukhtar, Labousse, Eddi, Fort and Couder2014). This is demonstrated in figure 7, where we simulate from the unstable steady state (with no real unstable eigenvalues), and nonlinear effects keep the droplets in a steady oscillatory bound state. Such a result was speculated on by Borghesi et al. (Reference Borghesi, Moukhtar, Labousse, Eddi, Fort and Couder2014), but is hard to observe experimentally due to the confines of a finite domain. The size of these oscillations depends on the skidding friction
$\unicode[STIX]{x1D6E4}$
. When there is an oscillatory instability (with no real eigenvalue), we expect the droplets to become bound in parallel motion, but with a transverse oscillation, as reported in experiments (Protière et al.
Reference Protière, Boudaoud and Couder2006; Borghesi et al.
Reference Borghesi, Moukhtar, Labousse, Eddi, Fort and Couder2014). This is demonstrated in figure 7, where we simulate from the unstable steady state (with no real unstable eigenvalues), and nonlinear effects keep the droplets in a steady oscillatory bound state. Such a result was speculated on by Borghesi et al. (Reference Borghesi, Moukhtar, Labousse, Eddi, Fort and Couder2014), but is hard to observe experimentally due to the confines of a finite domain. The size of these oscillations depends on the skidding friction
![]() $c$
and phase shift
$c$
and phase shift
![]() $\unicode[STIX]{x1D6FD}$
free parameters, which would both be tuned for a more careful comparison with experimental data. Larger
$\unicode[STIX]{x1D6FD}$
free parameters, which would both be tuned for a more careful comparison with experimental data. Larger
![]() $c$
increases the solution space for oscillatory pairs, and the transverse extent of the oscillations is reduced.
$c$
increases the solution space for oscillatory pairs, and the transverse extent of the oscillations is reduced.
To shed light on the instability of straight-line promenaders, we construct a new wave field based on the superposition of two parallel walkers (from § 5), and compare the average wave field energy over one impact period (appendix B). The distance between each walker is given by the continuous parameter
![]() $D$
. The antiphase case requires a mid-period impact for the second droplet; this presents a minor difficulty as we do not know the speed of the newly constructed walking pair, so the impact location is unknown (it should be recalled that a promenading pair travels slower than a single walker). For ease, we assume that the pair of walkers travel at the same speed as a single walker, which determines the impact location. We note that any error for this impact is small, and as the energy is a quadratic function of the wave amplitudes, this gives a negligible change to the energy.
$D$
. The antiphase case requires a mid-period impact for the second droplet; this presents a minor difficulty as we do not know the speed of the newly constructed walking pair, so the impact location is unknown (it should be recalled that a promenading pair travels slower than a single walker). For ease, we assume that the pair of walkers travel at the same speed as a single walker, which determines the impact location. We note that any error for this impact is small, and as the energy is a quadratic function of the wave amplitudes, this gives a negligible change to the energy.
Results of this calculation are shown in figure 8. Intuitively, we expect the energy of the walking pair to be minimised at the same distance as that of the promenading pair. However, the walking pair do not obey the condition
![]() $\unicode[STIX]{x2202}_{y}\unicode[STIX]{x1D702}=0$
at each droplet, which is required for a parallel procession. Hence, additional energy must be stored in the wave field in the case of the quantised promenaders, whose energy range (with
$\unicode[STIX]{x2202}_{y}\unicode[STIX]{x1D702}=0$
at each droplet, which is required for a parallel procession. Hence, additional energy must be stored in the wave field in the case of the quantised promenaders, whose energy range (with
![]() $\unicode[STIX]{x1D6E4}$
) is denoted by the thick black lines in figure 8. The difference in energy decreases as
$\unicode[STIX]{x1D6E4}$
) is denoted by the thick black lines in figure 8. The difference in energy decreases as
![]() $D$
increases due to the spatial decay of the wave field of the walker. Physically, the wave field would tend to adopt the lowest-energy state of two walkers; however, as this motion cannot be rectilinear (since
$D$
increases due to the spatial decay of the wave field of the walker. Physically, the wave field would tend to adopt the lowest-energy state of two walkers; however, as this motion cannot be rectilinear (since
![]() $\unicode[STIX]{x2202}_{y}\unicode[STIX]{x1D702}\neq 0$
at each droplet impact), a transverse oscillation ensues.
$\unicode[STIX]{x2202}_{y}\unicode[STIX]{x1D702}\neq 0$
at each droplet impact), a transverse oscillation ensues.

Figure 7. Example transition from an unstable straight-line promenade (starting at
![]() $x=0$
) to a stable oscillating promenade, with the speed given by the grey scale bar.
$x=0$
) to a stable oscillating promenade, with the speed given by the grey scale bar.

Figure 8. Wave field energy
![]() $E/E_{W}$
(relative to a single walker) for two in-phase (black) and antiphase (grey) parallel walkers at a distance
$E/E_{W}$
(relative to a single walker) for two in-phase (black) and antiphase (grey) parallel walkers at a distance
![]() $D$
apart for different values of
$D$
apart for different values of
![]() $\unicode[STIX]{x1D6E4}$
. The larger values of
$\unicode[STIX]{x1D6E4}$
. The larger values of
![]() $\unicode[STIX]{x1D6E4}$
give the most extreme variations in energy (
$\unicode[STIX]{x1D6E4}$
give the most extreme variations in energy (
![]() $\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6E4}_{F}=0.88,0.9,\ldots ,0.98$
). The thick black lines give the energy of the corresponding quantised parallel promenade solutions. The required interaction energy for the promenade mode partially explains its instability.
$\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6E4}_{F}=0.88,0.9,\ldots ,0.98$
). The thick black lines give the energy of the corresponding quantised parallel promenade solutions. The required interaction energy for the promenade mode partially explains its instability.
6.4 Droplet trains
Trains of droplets may be studied in a similar fashion to promenades, except that all droplets lie on the
![]() $x$
-axis and are spaced
$x$
-axis and are spaced
![]() $\unicode[STIX]{x1D6FF}s$
apart. This requires constant
$\unicode[STIX]{x1D6FF}s$
apart. This requires constant
![]() $\unicode[STIX]{x2202}_{x}\unicode[STIX]{x1D702}$
at each droplet, with the in-phase and antiphase results shown in figure 6(b), where we denote
$\unicode[STIX]{x2202}_{x}\unicode[STIX]{x1D702}$
at each droplet, with the in-phase and antiphase results shown in figure 6(b), where we denote
![]() $D\equiv \unicode[STIX]{x1D6FF}s$
. For sufficiently large
$D\equiv \unicode[STIX]{x1D6FF}s$
. For sufficiently large
![]() $\unicode[STIX]{x1D6E4}$
, two droplets may walk faster than a single droplet, which was also observed for experiments in a confined annulus (Filoux, Hubert & Vandewalle Reference Filoux, Hubert and Vandewalle2015). The stability types reported in figure 6(b) are for general perturbations, although the droplet trains are neutrally stable in the direction of travel (like a single walking droplet). Interestingly, the presence of a second droplet stabilises the system to general perturbations for some antiphase trains. A possible extension is to consider trains of multiple droplets, as considered in an annulus by Filoux et al. (Reference Filoux, Hubert and Vandewalle2015).
$\unicode[STIX]{x1D6E4}$
, two droplets may walk faster than a single droplet, which was also observed for experiments in a confined annulus (Filoux, Hubert & Vandewalle Reference Filoux, Hubert and Vandewalle2015). The stability types reported in figure 6(b) are for general perturbations, although the droplet trains are neutrally stable in the direction of travel (like a single walking droplet). Interestingly, the presence of a second droplet stabilises the system to general perturbations for some antiphase trains. A possible extension is to consider trains of multiple droplets, as considered in an annulus by Filoux et al. (Reference Filoux, Hubert and Vandewalle2015).
7 Droplet dynamics under a central force
When a droplet is subjected to a central force (
![]() $\tilde{\unicode[STIX]{x1D705}}>0$
in (3.24)), a range of new dynamics occur. For increasing
$\tilde{\unicode[STIX]{x1D705}}>0$
in (3.24)), a range of new dynamics occur. For increasing
![]() $\unicode[STIX]{x1D6E4}$
, a bouncing droplet may destabilise to a circular orbit, which itself destabilises to a variety of trajectories whose average radius and angular momentum are quantised (Perrard et al.
Reference Perrard, Labousse, Miskin, Fort and Couder2014b
). Analysis for circular orbits is analogous to § 6.1, but the more complex dynamics are explored numerically.
$\unicode[STIX]{x1D6E4}$
, a bouncing droplet may destabilise to a circular orbit, which itself destabilises to a variety of trajectories whose average radius and angular momentum are quantised (Perrard et al.
Reference Perrard, Labousse, Miskin, Fort and Couder2014b
). Analysis for circular orbits is analogous to § 6.1, but the more complex dynamics are explored numerically.
7.1 Circular orbits
For a single droplet in a circular orbit, the wave amplitudes must satisfy the rotational maps (6.4a,b
), and are governed by (3.22)–(3.23) with jump conditions (3.25)–(3.26). However, as
![]() $\tilde{\unicode[STIX]{x1D705}}>0$
, the droplet rotation condition (6.6) becomes
$\tilde{\unicode[STIX]{x1D705}}>0$
, the droplet rotation condition (6.6) becomes
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle F(c)\left(\frac{\unicode[STIX]{x1D707}_{+}\text{e}^{\unicode[STIX]{x1D707}_{+}}-\unicode[STIX]{x1D707}_{-}\text{e}^{\unicode[STIX]{x1D707}_{-}}}{\unicode[STIX]{x1D707}_{+}-\unicode[STIX]{x1D707}_{-}}\unicode[STIX]{x1D63F}(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703})-\text{e}^{-\tilde{\unicode[STIX]{x1D708}}_{p}}\unicode[STIX]{x1D644}_{2}\right)\boldsymbol{X}(t_{n})+(\unicode[STIX]{x1D63F}(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703})-\text{e}^{\unicode[STIX]{x1D707}_{+}}\unicode[STIX]{x1D644}_{2})(\unicode[STIX]{x1D63F}(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703})-\text{e}^{\unicode[STIX]{x1D707}_{-}}\unicode[STIX]{x1D644}_{2})\boldsymbol{X}(t_{n})\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad =\frac{-F(c)}{c}\sqrt{\frac{B}{R}}\left(\frac{\text{e}^{\unicode[STIX]{x1D707}_{+}}-\text{e}^{\unicode[STIX]{x1D707}_{-}}}{\unicode[STIX]{x1D707}_{+}-\unicode[STIX]{x1D707}_{-}}\right)\unicode[STIX]{x1D63F}(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703})(\unicode[STIX]{x1D735}\unicode[STIX]{x1D702})_{n},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle F(c)\left(\frac{\unicode[STIX]{x1D707}_{+}\text{e}^{\unicode[STIX]{x1D707}_{+}}-\unicode[STIX]{x1D707}_{-}\text{e}^{\unicode[STIX]{x1D707}_{-}}}{\unicode[STIX]{x1D707}_{+}-\unicode[STIX]{x1D707}_{-}}\unicode[STIX]{x1D63F}(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703})-\text{e}^{-\tilde{\unicode[STIX]{x1D708}}_{p}}\unicode[STIX]{x1D644}_{2}\right)\boldsymbol{X}(t_{n})+(\unicode[STIX]{x1D63F}(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703})-\text{e}^{\unicode[STIX]{x1D707}_{+}}\unicode[STIX]{x1D644}_{2})(\unicode[STIX]{x1D63F}(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703})-\text{e}^{\unicode[STIX]{x1D707}_{-}}\unicode[STIX]{x1D644}_{2})\boldsymbol{X}(t_{n})\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad =\frac{-F(c)}{c}\sqrt{\frac{B}{R}}\left(\frac{\text{e}^{\unicode[STIX]{x1D707}_{+}}-\text{e}^{\unicode[STIX]{x1D707}_{-}}}{\unicode[STIX]{x1D707}_{+}-\unicode[STIX]{x1D707}_{-}}\right)\unicode[STIX]{x1D63F}(\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703})(\unicode[STIX]{x1D735}\unicode[STIX]{x1D702})_{n},\end{eqnarray}$$
where
When
![]() $\unicode[STIX]{x1D707}_{\pm }\in \mathbb{C}$
, we use Euler’s formula to ensure a real solution, whose stability is analysed analogously to § 6.1. Example wave fields are given in figure 4(e,f).
$\unicode[STIX]{x1D707}_{\pm }\in \mathbb{C}$
, we use Euler’s formula to ensure a real solution, whose stability is analysed analogously to § 6.1. Example wave fields are given in figure 4(e,f).
We characterise this system with
![]() $\unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D6E4})\equiv \unicode[STIX]{x1D6FF}x(\unicode[STIX]{x1D6E4})/\sqrt{\tilde{\unicode[STIX]{x1D705}}}$
, where
$\unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D6E4})\equiv \unicode[STIX]{x1D6FF}x(\unicode[STIX]{x1D6E4})/\sqrt{\tilde{\unicode[STIX]{x1D705}}}$
, where
![]() $\unicode[STIX]{x1D6FF}x(\unicode[STIX]{x1D6E4})$
is the steady walking speed for
$\unicode[STIX]{x1D6FF}x(\unicode[STIX]{x1D6E4})$
is the steady walking speed for
![]() $\tilde{\unicode[STIX]{x1D705}}=0$
. For a classical orbit, balancing the spring constant
$\tilde{\unicode[STIX]{x1D705}}=0$
. For a classical orbit, balancing the spring constant
![]() $\tilde{\unicode[STIX]{x1D705}}$
and centripetal acceleration gives the orbit radius
$\tilde{\unicode[STIX]{x1D705}}$
and centripetal acceleration gives the orbit radius
![]() $R_{d}=\unicode[STIX]{x1D6EC}$
. However, the droplet interaction with the wave field leads to a more complicated radius structure as
$R_{d}=\unicode[STIX]{x1D6EC}$
. However, the droplet interaction with the wave field leads to a more complicated radius structure as
![]() $\unicode[STIX]{x1D6E4}$
increases (figure 9), where the unstable orbits require a larger average wave field energy. As with the in-phase orbiters, radii
$\unicode[STIX]{x1D6E4}$
increases (figure 9), where the unstable orbits require a larger average wave field energy. As with the in-phase orbiters, radii
![]() $R_{d}$
satisfying
$R_{d}$
satisfying
![]() $\text{J}_{0}(k_{F}R_{d})=0$
are solutions when
$\text{J}_{0}(k_{F}R_{d})=0$
are solutions when
![]() $\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E4}_{F}$
, which approximately correspond to the upper plateaus in figure 9(b). Noting that
$\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E4}_{F}$
, which approximately correspond to the upper plateaus in figure 9(b). Noting that
![]() $\unicode[STIX]{x1D6EC}=\infty$
corresponds to
$\unicode[STIX]{x1D6EC}=\infty$
corresponds to
![]() $\tilde{\unicode[STIX]{x1D705}}=0$
, figure 9(b) suggests that orbital solutions in the absence of a central force are possible for sufficiently high
$\tilde{\unicode[STIX]{x1D705}}=0$
, figure 9(b) suggests that orbital solutions in the absence of a central force are possible for sufficiently high
![]() $\unicode[STIX]{x1D6E4}$
. In the present parameter regime, self-orbiters are not stable; simulation from the self-orbiter initial conditions (
$\unicode[STIX]{x1D6E4}$
. In the present parameter regime, self-orbiters are not stable; simulation from the self-orbiter initial conditions (
![]() $R_{d}\approx 0.42$
) yields only two complete orbits at
$R_{d}\approx 0.42$
) yields only two complete orbits at
![]() $\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6E4}_{F}=0.994$
before the trajectory diverges.
$\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6E4}_{F}=0.994$
before the trajectory diverges.
When the circular orbits destabilise, a range of new orbits appear, with common examples shown in figure 10. In § 7.2, we see how these orbits manifest themselves at even larger
![]() $\unicode[STIX]{x1D6E4}$
, where all orbits are unstable.
$\unicode[STIX]{x1D6E4}$
, where all orbits are unstable.

Figure 9. Bifurcation diagram for orbit radius
![]() $R_{d}$
of a droplet in a harmonic potential well of width
$R_{d}$
of a droplet in a harmonic potential well of width
![]() $\unicode[STIX]{x1D6EC}$
. In (a),
$\unicode[STIX]{x1D6EC}$
. In (a),
![]() $\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6E4}_{F}=0.916$
(almost linear) and
$\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6E4}_{F}=0.916$
(almost linear) and
![]() $\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6E4}_{F}=0.975$
(snaked curve). In (b),
$\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6E4}_{F}=0.975$
(snaked curve). In (b),
![]() $\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6E4}_{F}=0.994$
. The lines correspond to stability types in table 2.
$\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6E4}_{F}=0.994$
. The lines correspond to stability types in table 2.

Figure 10. Example trajectories (lemniscate, trefoil and butterfly) for
![]() $\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6E4}_{F}\approx 0.975$
and different values of
$\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6E4}_{F}\approx 0.975$
and different values of
![]() $\unicode[STIX]{x1D6EC}$
. The colour bars indicate the speed of the droplet.
$\unicode[STIX]{x1D6EC}$
. The colour bars indicate the speed of the droplet.
7.2 Towards a double quantisation
As shown in the experiments of Perrard et al. (Reference Perrard, Labousse, Miskin, Fort and Couder2014b
), these exotic orbits exhibit a double quantisation in their mean radius and angular momentum in their stable states. The quantised states follow the same selection rule as the energy and angular momentum of a quantum particle in a two-dimensional potential well. Specifically, the radius and angular momentum form a
![]() $(p,q)$
lattice, where
$(p,q)$
lattice, where
![]() $p$
is an integer and
$p$
is an integer and
![]() $q\in \{-p,-p+2,\ldots ,p-2,p\}$
. These points correspond to the grey crosses
$q\in \{-p,-p+2,\ldots ,p-2,p\}$
. These points correspond to the grey crosses
![]() $(\times )$
in figures 11 and 12.
$(\times )$
in figures 11 and 12.
Although we obtain a similar quantisation for stable orbits, the methods of Perrard et al. (Reference Perrard, Labousse, Miskin, Fort and Couder2014b
) rely on a range of
![]() $\unicode[STIX]{x1D6E4}$
and
$\unicode[STIX]{x1D6E4}$
and
![]() $\unicode[STIX]{x1D6EC}$
in an unsystematic way. Instead, we explore the dynamics in the chaotic regime for fixed
$\unicode[STIX]{x1D6EC}$
in an unsystematic way. Instead, we explore the dynamics in the chaotic regime for fixed
![]() $\unicode[STIX]{x1D6E4}$
, whereby the observed orbits destabilise but continue to be recognisable over short time intervals. This allows for a novel and methodical analysis of the long-time dynamics, yielding a similar double quantisation.
$\unicode[STIX]{x1D6E4}$
, whereby the observed orbits destabilise but continue to be recognisable over short time intervals. This allows for a novel and methodical analysis of the long-time dynamics, yielding a similar double quantisation.

Figure 11. (a) Example clustering for a single trajectory with
![]() $\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6E4}_{F}=0.984$
and
$\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6E4}_{F}=0.984$
and
![]() $\unicode[STIX]{x1D6EC}=1.23$
. The light blue circles are averages over sections and the grey crosses form the approximate lattice for the quantum double quantisation. The red dots are the cluster centroids for this example (initially,
$\unicode[STIX]{x1D6EC}=1.23$
. The light blue circles are averages over sections and the grey crosses form the approximate lattice for the quantum double quantisation. The red dots are the cluster centroids for this example (initially,
![]() $R_{d}=1.75$
and
$R_{d}=1.75$
and
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703}>0$
). (b) The corresponding trajectory (grey) with example coloured sub-trajectories shown over short time intervals.
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703}>0$
). (b) The corresponding trajectory (grey) with example coloured sub-trajectories shown over short time intervals.

Figure 12. Double quantisation for a droplet in a harmonic potential for
![]() $\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6E4}_{F}=0.984$
. The grey crosses form the quantum double quantisation lattice and the red dots are the cluster centroids for simulations over all initial radii
$\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6E4}_{F}=0.984$
. The grey crosses form the quantum double quantisation lattice and the red dots are the cluster centroids for simulations over all initial radii
![]() $R_{d}\in \{0.4,0.425,\ldots ,2\}$
and corresponding values of
$R_{d}\in \{0.4,0.425,\ldots ,2\}$
and corresponding values of
![]() $\unicode[STIX]{x1D6EC}$
, with both
$\unicode[STIX]{x1D6EC}$
, with both
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703}>0$
and
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703}>0$
and
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703}<0$
initially.
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703}<0$
initially.
For a given circular orbit radius
![]() $R_{d}>0$
, there exist unique
$R_{d}>0$
, there exist unique
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703}>0$
,
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703}>0$
,
![]() $\unicode[STIX]{x1D6EC}>0$
and the corresponding wave field (see the example in figure 9(a) with
$\unicode[STIX]{x1D6EC}>0$
and the corresponding wave field (see the example in figure 9(a) with
![]() $\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6E4}_{F}=0.975$
). This provides a well-defined systematic initial condition for numerical simulation. We simulate over
$\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6E4}_{F}=0.975$
). This provides a well-defined systematic initial condition for numerical simulation. We simulate over
![]() $(N_{0}+N)$
impacts, where the first
$(N_{0}+N)$
impacts, where the first
![]() $N_{0}$
impacts are a ‘burn-in’ period (omitted from further analysis). This is the time allowed for the droplet to destabilise from its circular orbit and begin to explore the underlying probability distribution of the dynamics. Throughout this work, we fix
$N_{0}$
impacts are a ‘burn-in’ period (omitted from further analysis). This is the time allowed for the droplet to destabilise from its circular orbit and begin to explore the underlying probability distribution of the dynamics. Throughout this work, we fix
![]() $N_{0}=3000$
impacts and
$N_{0}=3000$
impacts and
![]() $N=3\times 10^{4}$
, where
$N=3\times 10^{4}$
, where
![]() $N_{0}$
is estimated by considering the unstable eigenvalues of the system and
$N_{0}$
is estimated by considering the unstable eigenvalues of the system and
![]() $N$
is large enough so that the resulting probability distribution is ergodic. For stable circular orbits, the droplet remains on its initial trajectory for all impacts. We perform this process for
$N$
is large enough so that the resulting probability distribution is ergodic. For stable circular orbits, the droplet remains on its initial trajectory for all impacts. We perform this process for
![]() $R_{d}\in \{0.4,0.425,\ldots ,2\}$
, which removes the stable orbits for small
$R_{d}\in \{0.4,0.425,\ldots ,2\}$
, which removes the stable orbits for small
![]() $\unicode[STIX]{x1D6EC}$
in which the central force dominates the trajectory. Simulation from initial conditions with
$\unicode[STIX]{x1D6EC}$
in which the central force dominates the trajectory. Simulation from initial conditions with
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703}<0$
does not yield a corresponding symmetric trajectory (as the dynamics are chaotic), but the statistics are unchanged.
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703}<0$
does not yield a corresponding symmetric trajectory (as the dynamics are chaotic), but the statistics are unchanged.
It remains to analyse the data from these trajectories. Following Perrard et al. (Reference Perrard, Labousse, Miskin, Fort and Couder2014b
), we define the dimensionless mean radius
![]() $\bar{R}$
and mean angular momentum
$\bar{R}$
and mean angular momentum
![]() $\bar{L}_{z}$
as
$\bar{L}_{z}$
as
where
![]() $r_{d}(t)$
is the droplet radius at time
$r_{d}(t)$
is the droplet radius at time
![]() $t$
and
$t$
and
![]() $\times$
denotes the vector product.
$\times$
denotes the vector product.
When simulating from an oscillatory instability, we expect to obtain wobbling circular orbits. However, when a real unstable eigenvalue exists, the trajectory is pushed away from the circular orbit, and more exotic dynamics occur. From the work of Perrard et al. (Reference Perrard, Labousse, Miskin, Fort and Couder2014b
), we expect to obtain trajectories that resemble lemniscates and trefoils on a short time scale, but appear chaotic on a long time scale (see the examples in figure 10). Although taking averages over all
![]() $N$
impacts makes some progress towards a double quantisation, trajectories with switching states (typically between lemniscates and ovals) blur this picture. As these states are non-constant and unstable, it is difficult to identify switching times without hand-picking the data (as in Perrard et al. (Reference Perrard, Labousse, Miskin, Fort and Couder2014b
)), so we seek an alternative approach.
$N$
impacts makes some progress towards a double quantisation, trajectories with switching states (typically between lemniscates and ovals) blur this picture. As these states are non-constant and unstable, it is difficult to identify switching times without hand-picking the data (as in Perrard et al. (Reference Perrard, Labousse, Miskin, Fort and Couder2014b
)), so we seek an alternative approach.
The answer lies in a further understanding of stable lemniscate and trefoil orbits. Our systematic analysis starts off by segmenting the long trajectory into shorter sections between the radial maxima of impacts. This yields well-defined cutting times. For a fictitious stable lemniscate, the mean radius and angular momentum are the same between two radial maxima compared with the whole trajectory (we have ‘half’ of a lemniscate). Similarly, the radial maxima break a fictitious stable trefoil into three identical sections (up to a rotation of
![]() $2\unicode[STIX]{x03C0}/3$
). For a stable circular orbit, each point is defined as a radial maximum. Hence, we proceed by splitting each trajectory into intervals between radial maxima, and compute
$2\unicode[STIX]{x03C0}/3$
). For a stable circular orbit, each point is defined as a radial maximum. Hence, we proceed by splitting each trajectory into intervals between radial maxima, and compute
![]() $\bar{R}$
and
$\bar{R}$
and
![]() $\bar{L}_{z}$
over each interval.
$\bar{L}_{z}$
over each interval.
For each trajectory, we may visualise the resulting interval mean data by plotting a scatter graph in the
![]() $(\bar{L}_{z},\bar{R})$
-plane (see the example in figure 11). Each trajectory gives rise to a well-separated set of clusters of mean radius and angular momentum points, where multiple clusters only arise in the case of switching states. This motivates cluster analysis as a suitable statistical approach to completing the double quantisation.
$(\bar{L}_{z},\bar{R})$
-plane (see the example in figure 11). Each trajectory gives rise to a well-separated set of clusters of mean radius and angular momentum points, where multiple clusters only arise in the case of switching states. This motivates cluster analysis as a suitable statistical approach to completing the double quantisation.
To calculate the clusters for each simulation, we use
![]() $K$
-means clustering, where
$K$
-means clustering, where
![]() $K$
is a predetermined number of clusters (Hartigan Reference Hartigan1975; Hartigan & Wong Reference Hartigan and Wong1979). The aim is to globally minimise the cost function, which is the total Euclidean distance between points. Each sub-trajectory is weighted by its number of impacts; this prevents smaller trajectories from being favoured (as radial maxima are achieved more frequently). The algorithm takes random initial locations for the cluster means (centroids) and is guaranteed to converge to a local minimum of the cost function. A sufficiently large number of repetitions is likely to locate the global minimum, which determines the locations of the centroids. When
$K$
is a predetermined number of clusters (Hartigan Reference Hartigan1975; Hartigan & Wong Reference Hartigan and Wong1979). The aim is to globally minimise the cost function, which is the total Euclidean distance between points. Each sub-trajectory is weighted by its number of impacts; this prevents smaller trajectories from being favoured (as radial maxima are achieved more frequently). The algorithm takes random initial locations for the cluster means (centroids) and is guaranteed to converge to a local minimum of the cost function. A sufficiently large number of repetitions is likely to locate the global minimum, which determines the locations of the centroids. When
![]() $K=1$
, this is simply the global mean of the data.
$K=1$
, this is simply the global mean of the data.
The issue with all clustering techniques is determining the value of
![]() $K$
. As it happens, the cases considered for this double quantisation can almost be identified by eye; the example in figure 11(a) has
$K$
. As it happens, the cases considered for this double quantisation can almost be identified by eye; the example in figure 11(a) has
![]() $K=5$
well-separated clusters. However, statistical techniques also exist as a guide for the number of clusters, such as the elbow method, silhouettes and cross-validation (Kodinariya & Makwana Reference Kodinariya and Makwana2013). However, the great benefit of clustering in this application is that the technique automatically groups together similar trajectories and averages over them. The outlier trajectories (say the transitions between lemniscates and ovals) are infrequent so do not skew the data.
$K=5$
well-separated clusters. However, statistical techniques also exist as a guide for the number of clusters, such as the elbow method, silhouettes and cross-validation (Kodinariya & Makwana Reference Kodinariya and Makwana2013). However, the great benefit of clustering in this application is that the technique automatically groups together similar trajectories and averages over them. The outlier trajectories (say the transitions between lemniscates and ovals) are infrequent so do not skew the data.
By combining the centroids from all of the simulations, we obtain a double quantisation in
![]() $(\bar{L}_{z},\bar{R})$
in the chaotic regime (
$(\bar{L}_{z},\bar{R})$
in the chaotic regime (
![]() $\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6E4}_{F}=0.984$
), as shown in figure 12. We note that Perrard et al. (Reference Perrard, Labousse, Miskin, Fort and Couder2014b
) also observed a less sharp quantisation for
$\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6E4}_{F}=0.984$
), as shown in figure 12. We note that Perrard et al. (Reference Perrard, Labousse, Miskin, Fort and Couder2014b
) also observed a less sharp quantisation for
![]() $\bar{R}>2$
. There is a notable dearth of centroids around
$\bar{R}>2$
. There is a notable dearth of centroids around
![]() $(\pm 0.5,1.5)$
; the loop tractories corresponding to this quantisation are unstable and only exist for much larger values of
$(\pm 0.5,1.5)$
; the loop tractories corresponding to this quantisation are unstable and only exist for much larger values of
![]() $\unicode[STIX]{x1D6E4}$
considered. The loops are the combination of straight-line solutions and spin states, whereby a single droplet may orbit itself in the absence of a central force. The existence of these unstable spin states can be seen from figure 9(b) for large
$\unicode[STIX]{x1D6E4}$
considered. The loops are the combination of straight-line solutions and spin states, whereby a single droplet may orbit itself in the absence of a central force. The existence of these unstable spin states can be seen from figure 9(b) for large
![]() $\unicode[STIX]{x1D6EC}$
(corresponding to small
$\unicode[STIX]{x1D6EC}$
(corresponding to small
![]() $\tilde{\unicode[STIX]{x1D705}}$
). However, the centroids at approximately
$\tilde{\unicode[STIX]{x1D705}}$
). However, the centroids at approximately
![]() $(\pm 1,1.5)$
are stable trefoil-like features not reported in Perrard et al. (Reference Perrard, Labousse, Miskin, Fort and Couder2014b
). A more thorough investigation may lead to the discovery of new trajectories that alter the shape of the double quantisation.
$(\pm 1,1.5)$
are stable trefoil-like features not reported in Perrard et al. (Reference Perrard, Labousse, Miskin, Fort and Couder2014b
). A more thorough investigation may lead to the discovery of new trajectories that alter the shape of the double quantisation.
8 Discussion
We have derived a new discrete-time model for the Faraday wave–droplet interactions on a vibrating bath, yielding stability analysis of fixed points, with many bifurcations explained through energy considerations. The map structure also allows us to explore the statistics of the system through extremely efficient numerical simulations. By analysing bouncing and walking states, we captured an improved wave field that exhibits a Doppler effect, exponential spatial damping and the travelling capillary wave from a single impact. These features are not present in the trajectory equation of Oza et al. (Reference Oza, Rosales and Bush2013).
For two interacting droplets, we modelled orbiters, promenade pairs and droplet trains. For orbiters, we identified the experimentally observed quantisation for the orbit diameter and analysed the stability. By considering the unstable upper branch for each orbit, we obtained an upper bound for the extent of stable wobbly orbits. This gives a partial explanation for the restricted existence of these states. We also showed that straight-line promenade pairs are unstable, but for weak oscillatory instabilities it is possible to transition from straight-line promenades to promenades with transverse oscillations, as hypothesised by Borghesi et al. (Reference Borghesi, Moukhtar, Labousse, Eddi, Fort and Couder2014). We performed the first analysis for droplet trains in an unbounded domain, and showed that in a certain parameter regime, the train travels faster than a single droplet. This feature was also observed in the annulus experiments of Filoux et al. (Reference Filoux, Hubert and Vandewalle2015).
Finally, we explored the dynamics of a droplet in a harmonic potential. We studied the stability of circular orbits and obtained similar results to Labousse et al. (Reference Labousse, Oza, Perrard and Bush2016). By simulating in the chaotic regime and exploiting cluster analysis, we showed that the trajectories obey a double quantisation for a single value of
![]() $\unicode[STIX]{x1D6E4}$
.
$\unicode[STIX]{x1D6E4}$
.
Despite the success of this model in a variety of situations, the dynamics are still restricted to the
![]() $(2,1)$
mode with prescribed impact phase. In the future, we aim to relax this restriction while maintaining instantaneous impacts to allow for mathematical analysis akin to this work. This will allow us to explore the bifurcation between a range of
$(2,1)$
mode with prescribed impact phase. In the future, we aim to relax this restriction while maintaining instantaneous impacts to allow for mathematical analysis akin to this work. This will allow us to explore the bifurcation between a range of
![]() $(m,n)$
impact modes, with a self-selecting impact phase. Furthermore, as we have only considered an unbounded fluid domain, we are unable to model the interaction with submerged obstacles, such as slits and barriers. Future work on this will lend far greater insight into the experimentally observed diffraction and interference patterns (Couder & Fort Reference Couder and Fort2006), tunnelling (Eddi et al.
Reference Eddi, Fort, Moisy and Couder2009) and the droplet probability distribution in a quantum-like corral (Harris et al.
Reference Harris, Moukhtar, Fort, Couder and Bush2013).
$(m,n)$
impact modes, with a self-selecting impact phase. Furthermore, as we have only considered an unbounded fluid domain, we are unable to model the interaction with submerged obstacles, such as slits and barriers. Future work on this will lend far greater insight into the experimentally observed diffraction and interference patterns (Couder & Fort Reference Couder and Fort2006), tunnelling (Eddi et al.
Reference Eddi, Fort, Moisy and Couder2009) and the droplet probability distribution in a quantum-like corral (Harris et al.
Reference Harris, Moukhtar, Fort, Couder and Bush2013).
Acknowledgements
The authors thank J. Bush, C. Galeano-Rios, A. Oza and R. Rosales for useful contributions and discussions. M.D. gratefully acknowledges support through a scholarship from the EPSRC Centre for Doctoral Training in Statistical Applied Mathematics at Bath (SAMBa) under the project EP/L015684/1. P.A.M. gratefully acknowledges support through the EPSRC project EP/N018176/1 and a Royal Society Wolfson award.
Appendix A. Derivation of the droplet jump condition
For ease, we generalise (3.20) to the scalar differential equation
where
![]() ${\mathcal{F}}$
is bounded and piecewise smooth except for a jump in
${\mathcal{F}}$
is bounded and piecewise smooth except for a jump in
![]() $\unicode[STIX]{x2202}{\mathcal{F}}/\unicode[STIX]{x2202}t$
at
$\unicode[STIX]{x2202}{\mathcal{F}}/\unicode[STIX]{x2202}t$
at
![]() $t=t^{\star }>0$
. We assume that
$t=t^{\star }>0$
. We assume that
![]() ${\mathcal{G}}$
is bounded along a solution to (A 1) over the interval
${\mathcal{G}}$
is bounded along a solution to (A 1) over the interval
![]() $(0,t)$
, including at
$(0,t)$
, including at
![]() $t=t_{\star }$
. Catllá et al. (Reference Catllá, Schaeffer, Witelski, Monson and Lin2008) considered the special case
$t=t_{\star }$
. Catllá et al. (Reference Catllá, Schaeffer, Witelski, Monson and Lin2008) considered the special case
![]() ${\mathcal{G}}=-u^{\prime }(t)$
and constant forcing
${\mathcal{G}}=-u^{\prime }(t)$
and constant forcing
![]() ${\mathcal{F}}$
.
${\mathcal{F}}$
.
We define a generalised
![]() $\unicode[STIX]{x1D6FF}$
-function
$\unicode[STIX]{x1D6FF}$
-function
![]() $\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D700}}$
and corresponding Heaviside function
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D700}}$
and corresponding Heaviside function
![]() $H_{\unicode[STIX]{x1D700}}$
as
$H_{\unicode[STIX]{x1D700}}$
as
where
![]() $\unicode[STIX]{x1D711}(s)\geqslant 0$
for all
$\unicode[STIX]{x1D711}(s)\geqslant 0$
for all
![]() $s\in \mathbb{R}$
and
$s\in \mathbb{R}$
and
![]() $\int _{-\infty }^{\infty }\unicode[STIX]{x1D711}(s)\,\text{d}s$
= 1. We will integrate (A 1) once to give an integro-differential equation for the cases
$\int _{-\infty }^{\infty }\unicode[STIX]{x1D711}(s)\,\text{d}s$
= 1. We will integrate (A 1) once to give an integro-differential equation for the cases
![]() $t<t_{\star }$
and
$t<t_{\star }$
and
![]() $t>t_{\star }$
. By taking the limits
$t>t_{\star }$
. By taking the limits
![]() $\unicode[STIX]{x1D700}\rightarrow 0$
and
$\unicode[STIX]{x1D700}\rightarrow 0$
and
![]() $t\rightarrow t_{\star }^{\pm }$
, we obtain the jump
$t\rightarrow t_{\star }^{\pm }$
, we obtain the jump
![]() $[u^{\prime }(t_{\star })]_{-}^{+}$
, which is independent of
$[u^{\prime }(t_{\star })]_{-}^{+}$
, which is independent of
![]() $\unicode[STIX]{x1D711}$
.
$\unicode[STIX]{x1D711}$
.
For
![]() $t<t_{\star }$
, (A 1) simplifies to
$t<t_{\star }$
, (A 1) simplifies to
![]() $u^{\prime \prime }(t)={\mathcal{G}}$
. Integrating once yields
$u^{\prime \prime }(t)={\mathcal{G}}$
. Integrating once yields
![]() $u^{\prime }(t)=u^{\prime }(0)+\int _{0}^{t}{\mathcal{G}},$
which gives
$u^{\prime }(t)=u^{\prime }(0)+\int _{0}^{t}{\mathcal{G}},$
which gives
![]() $u^{\prime }(t_{\star }^{-})=u^{\prime }(0)+\int _{0}^{t_{\star }}{\mathcal{G}}.$
For
$u^{\prime }(t_{\star }^{-})=u^{\prime }(0)+\int _{0}^{t_{\star }}{\mathcal{G}}.$
For
![]() $t>t_{\star }$
, we replace
$t>t_{\star }$
, we replace
![]() $\unicode[STIX]{x1D6FF}$
with
$\unicode[STIX]{x1D6FF}$
with
![]() $\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D700}}$
in (A 1) and use the integrating factor
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D700}}$
in (A 1) and use the integrating factor
![]() $\text{e}^{CH_{\unicode[STIX]{x1D700}}(t-t_{\star })}$
to obtain
$\text{e}^{CH_{\unicode[STIX]{x1D700}}(t-t_{\star })}$
to obtain
![]() $u^{\prime }(t)\text{e}^{CH_{\unicode[STIX]{x1D700}}(t-t_{\star })}=I_{1}(t)+I_{2}(t)$
, where
$u^{\prime }(t)\text{e}^{CH_{\unicode[STIX]{x1D700}}(t-t_{\star })}=I_{1}(t)+I_{2}(t)$
, where
In
![]() $I_{1}(t)$
, the integrand is bounded almost everywhere and is integrable over
$I_{1}(t)$
, the integrand is bounded almost everywhere and is integrable over
![]() $[0,t]$
, so for
$[0,t]$
, so for
![]() $t<\infty$
the bounded convergence theorem gives
$t<\infty$
the bounded convergence theorem gives
![]() $\lim _{\unicode[STIX]{x1D700}\rightarrow 0}I_{1}(t)=u^{\prime }(0)+\int _{0}^{t_{\star }}{\mathcal{G}}+\text{e}^{C}\int _{t_{\star }}^{t}{\mathcal{G}}$
. Hence,
$\lim _{\unicode[STIX]{x1D700}\rightarrow 0}I_{1}(t)=u^{\prime }(0)+\int _{0}^{t_{\star }}{\mathcal{G}}+\text{e}^{C}\int _{t_{\star }}^{t}{\mathcal{G}}$
. Hence,
![]() $I_{1}(t_{\star }^{+})=u^{\prime }(t_{\star }^{-})$
.
$I_{1}(t_{\star }^{+})=u^{\prime }(t_{\star }^{-})$
.
The integral for
![]() $I_{2}(t)$
is more delicate. To proceed, we split the integral
$I_{2}(t)$
is more delicate. To proceed, we split the integral
![]() $\int _{0}^{t}=\int _{0}^{t_{\star }-\unicode[STIX]{x1D709}}+\int _{t_{\star }-\unicode[STIX]{x1D709}}^{t_{\star }+\unicode[STIX]{x1D709}}+\int _{t_{\star }+\unicode[STIX]{x1D709}}^{t}$
, for some suitable
$\int _{0}^{t}=\int _{0}^{t_{\star }-\unicode[STIX]{x1D709}}+\int _{t_{\star }-\unicode[STIX]{x1D709}}^{t_{\star }+\unicode[STIX]{x1D709}}+\int _{t_{\star }+\unicode[STIX]{x1D709}}^{t}$
, for some suitable
![]() $\unicode[STIX]{x1D709}>0$
, where the two outer integrals tend to zero as
$\unicode[STIX]{x1D709}>0$
, where the two outer integrals tend to zero as
![]() $\unicode[STIX]{x1D709}\rightarrow 0$
for any
$\unicode[STIX]{x1D709}\rightarrow 0$
for any
![]() $\unicode[STIX]{x1D700}>0$
. This is shown by first using the boundedness of
$\unicode[STIX]{x1D700}>0$
. This is shown by first using the boundedness of
![]() ${\mathcal{F}}$
and
${\mathcal{F}}$
and
![]() $H_{\unicode[STIX]{x1D700}}(s)\leqslant 1$
, which results in an integral over
$H_{\unicode[STIX]{x1D700}}(s)\leqslant 1$
, which results in an integral over
![]() $\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D700}}$
. The final stage is to substitute in the definition of
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D700}}$
. The final stage is to substitute in the definition of
![]() $\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D700}}$
, change variables
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D700}}$
, change variables
![]() $\unicode[STIX]{x1D70F}=(s-t_{\star })/\unicode[STIX]{x1D700}$
and use the fact that
$\unicode[STIX]{x1D70F}=(s-t_{\star })/\unicode[STIX]{x1D700}$
and use the fact that
![]() $\unicode[STIX]{x1D711}(\pm \infty )=0$
.
$\unicode[STIX]{x1D711}(\pm \infty )=0$
.
We now examine the behaviour of the integral
![]() $\int _{t_{\star }-\unicode[STIX]{x1D709}}^{t_{\star }+\unicode[STIX]{x1D709}}$
in the limit
$\int _{t_{\star }-\unicode[STIX]{x1D709}}^{t_{\star }+\unicode[STIX]{x1D709}}$
in the limit
![]() $\unicode[STIX]{x1D700}\rightarrow 0$
. As
$\unicode[STIX]{x1D700}\rightarrow 0$
. As
we integrate by parts to obtain
where
By assumption,
![]() $\text{d}{\mathcal{F}}/\text{d}s$
is continuous except at
$\text{d}{\mathcal{F}}/\text{d}s$
is continuous except at
![]() $t=t^{\star }$
and bounded everywhere. Hence, the bounded convergence theorem allows us to take the limit
$t=t^{\star }$
and bounded everywhere. Hence, the bounded convergence theorem allows us to take the limit
![]() $\unicode[STIX]{x1D700}\rightarrow 0$
inside both integrals, which can both be integrated directly by properties of the Heaviside function
$\unicode[STIX]{x1D700}\rightarrow 0$
inside both integrals, which can both be integrated directly by properties of the Heaviside function
![]() $H(s-t_{\star })$
. Now, taking
$H(s-t_{\star })$
. Now, taking
![]() $\unicode[STIX]{x1D709}\rightarrow 0$
, we use continuity of
$\unicode[STIX]{x1D709}\rightarrow 0$
, we use continuity of
![]() ${\mathcal{F}}$
to show that
${\mathcal{F}}$
to show that
![]() $\lim _{\unicode[STIX]{x1D709}\rightarrow 0}\lim _{\unicode[STIX]{x1D700}\rightarrow 0}Q_{\unicode[STIX]{x1D700},\unicode[STIX]{x1D709}}=0$
. In this same limiting order, we can evaluate the term
$\lim _{\unicode[STIX]{x1D709}\rightarrow 0}\lim _{\unicode[STIX]{x1D700}\rightarrow 0}Q_{\unicode[STIX]{x1D700},\unicode[STIX]{x1D709}}=0$
. In this same limiting order, we can evaluate the term
![]() $[\cdot ]_{t_{\star }-\unicode[STIX]{x1D709}}^{t_{\star }+\unicode[STIX]{x1D709}}$
in (A 5).
$[\cdot ]_{t_{\star }-\unicode[STIX]{x1D709}}^{t_{\star }+\unicode[STIX]{x1D709}}$
in (A 5).
Therefore, in the limit
![]() $\unicode[STIX]{x1D700}\rightarrow 0$
, we combine these results and take
$\unicode[STIX]{x1D700}\rightarrow 0$
, we combine these results and take
![]() $t\rightarrow t_{\star }^{+}$
. This gives
$t\rightarrow t_{\star }^{+}$
. This gives
![]() $u^{\prime }(t_{\star }^{+})\text{e}^{C}=u^{\prime }(t_{\star }^{-})+C^{-1}{\mathcal{F}}(t_{\star },u(t_{\star }))(\text{e}^{C}-1)$
. Multiplying through by
$u^{\prime }(t_{\star }^{+})\text{e}^{C}=u^{\prime }(t_{\star }^{-})+C^{-1}{\mathcal{F}}(t_{\star },u(t_{\star }))(\text{e}^{C}-1)$
. Multiplying through by
![]() $\text{e}^{-C}$
and subtracting
$\text{e}^{-C}$
and subtracting
![]() $u^{\prime }(t_{\star }^{-})$
from both sides gives the required jump
$u^{\prime }(t_{\star }^{-})$
from both sides gives the required jump
It should be noted that the jump is independent of
![]() ${\mathcal{G}}$
and the choice of
${\mathcal{G}}$
and the choice of
![]() $\unicode[STIX]{x1D711}$
. In the limit
$\unicode[STIX]{x1D711}$
. In the limit
![]() $C\rightarrow 0$
, we obtain
$C\rightarrow 0$
, we obtain
![]() $[u^{\prime }(t_{\star })]_{-}^{+}={\mathcal{F}}(t_{\star },u(t_{\star }))$
, which is consistent with the original formulation.
$[u^{\prime }(t_{\star })]_{-}^{+}={\mathcal{F}}(t_{\star },u(t_{\star }))$
, which is consistent with the original formulation.
Appendix B. The energy of the wave field
We briefly derive the energy perturbation created by the presence of the droplet and associated waves (in dimensional variables). The perturbed surface energy is
for small perturbations. By noting that
![]() $|\unicode[STIX]{x1D735}\unicode[STIX]{x1D702}|^{2}=\unicode[STIX]{x1D735}\boldsymbol{\cdot }(\unicode[STIX]{x1D702}\unicode[STIX]{x1D735}\unicode[STIX]{x1D702})-\unicode[STIX]{x1D702}\unicode[STIX]{x1D6FB}_{H}^{2}\unicode[STIX]{x1D702}$
and that
$|\unicode[STIX]{x1D735}\unicode[STIX]{x1D702}|^{2}=\unicode[STIX]{x1D735}\boldsymbol{\cdot }(\unicode[STIX]{x1D702}\unicode[STIX]{x1D735}\unicode[STIX]{x1D702})-\unicode[STIX]{x1D702}\unicode[STIX]{x1D6FB}_{H}^{2}\unicode[STIX]{x1D702}$
and that
![]() $\unicode[STIX]{x1D702}\rightarrow 0$
as
$\unicode[STIX]{x1D702}\rightarrow 0$
as
![]() $|\boldsymbol{x}|\rightarrow \infty$
, an application of Green’s theorem yields
$|\boldsymbol{x}|\rightarrow \infty$
, an application of Green’s theorem yields
For the gravitational potential energy, we introduce variables
![]() $\unicode[STIX]{x1D701}$
and
$\unicode[STIX]{x1D701}$
and
![]() $\tilde{\unicode[STIX]{x1D702}}$
to represent
$\tilde{\unicode[STIX]{x1D702}}$
to represent
![]() $z$
and
$z$
and
![]() $\unicode[STIX]{x1D702}$
in the stationary frame. Specifically, we define
$\unicode[STIX]{x1D702}$
in the stationary frame. Specifically, we define
![]() $\unicode[STIX]{x1D701}=z+A\cos (\unicode[STIX]{x1D714}_{0}t+\unicode[STIX]{x1D6FD})$
and
$\unicode[STIX]{x1D701}=z+A\cos (\unicode[STIX]{x1D714}_{0}t+\unicode[STIX]{x1D6FD})$
and
![]() $\tilde{\unicode[STIX]{x1D702}}=\unicode[STIX]{x1D702}+A\cos (\unicode[STIX]{x1D714}_{0}t+\unicode[STIX]{x1D6FD}).$
Without loss of generality, we set the gravitational energy to be zero at
$\tilde{\unicode[STIX]{x1D702}}=\unicode[STIX]{x1D702}+A\cos (\unicode[STIX]{x1D714}_{0}t+\unicode[STIX]{x1D6FD}).$
Without loss of generality, we set the gravitational energy to be zero at
![]() $\unicode[STIX]{x1D701}=0$
. Thus,
$\unicode[STIX]{x1D701}=0$
. Thus,
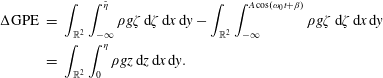 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x0394}\text{GPE} & = & \displaystyle \int _{\mathbb{R}^{2}}\int _{-\infty }^{\tilde{\unicode[STIX]{x1D702}}}\unicode[STIX]{x1D70C}g\unicode[STIX]{x1D701}\,\text{d}\unicode[STIX]{x1D701}\,\text{d}x\,\text{d}y-\int _{\mathbb{R}^{2}}\int _{-\infty }^{A\cos (\unicode[STIX]{x1D714}_{0}t+\unicode[STIX]{x1D6FD})}\unicode[STIX]{x1D70C}g\unicode[STIX]{x1D701}\,\text{d}\unicode[STIX]{x1D701}\,\text{d}x\,\text{d}y\nonumber\\ \displaystyle & = & \displaystyle \int _{\mathbb{R}^{2}}\int _{0}^{\unicode[STIX]{x1D702}}\unicode[STIX]{x1D70C}gz\,\text{d}z\,\text{d}x\,\text{d}y.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x0394}\text{GPE} & = & \displaystyle \int _{\mathbb{R}^{2}}\int _{-\infty }^{\tilde{\unicode[STIX]{x1D702}}}\unicode[STIX]{x1D70C}g\unicode[STIX]{x1D701}\,\text{d}\unicode[STIX]{x1D701}\,\text{d}x\,\text{d}y-\int _{\mathbb{R}^{2}}\int _{-\infty }^{A\cos (\unicode[STIX]{x1D714}_{0}t+\unicode[STIX]{x1D6FD})}\unicode[STIX]{x1D70C}g\unicode[STIX]{x1D701}\,\text{d}\unicode[STIX]{x1D701}\,\text{d}x\,\text{d}y\nonumber\\ \displaystyle & = & \displaystyle \int _{\mathbb{R}^{2}}\int _{0}^{\unicode[STIX]{x1D702}}\unicode[STIX]{x1D70C}gz\,\text{d}z\,\text{d}x\,\text{d}y.\end{eqnarray}$$
Hence,
It should be noted that the velocity potential
![]() $\unicode[STIX]{x1D719}$
is defined in the vibrating frame, and
$\unicode[STIX]{x1D719}$
is defined in the vibrating frame, and
![]() $|\unicode[STIX]{x1D735}\unicode[STIX]{x1D719}|=\mathbf{0}$
when there are no waves. Hence, by neglecting the energy from the small vortical component near the surface, the kinetic energy perturbation is
$|\unicode[STIX]{x1D735}\unicode[STIX]{x1D719}|=\mathbf{0}$
when there are no waves. Hence, by neglecting the energy from the small vortical component near the surface, the kinetic energy perturbation is
By the continuity equation (2.1),
![]() $|\unicode[STIX]{x1D735}\unicode[STIX]{x1D719}|^{2}=\unicode[STIX]{x1D735}\boldsymbol{\cdot }(\unicode[STIX]{x1D719}\unicode[STIX]{x1D735}\unicode[STIX]{x1D719})$
. As
$|\unicode[STIX]{x1D735}\unicode[STIX]{x1D719}|^{2}=\unicode[STIX]{x1D735}\boldsymbol{\cdot }(\unicode[STIX]{x1D719}\unicode[STIX]{x1D735}\unicode[STIX]{x1D719})$
. As
![]() $|\unicode[STIX]{x1D735}\unicode[STIX]{x1D719}|\rightarrow \mathbf{0}$
in the far field, we apply the divergence theorem to reduce the problem to the surface integral
$|\unicode[STIX]{x1D735}\unicode[STIX]{x1D719}|\rightarrow \mathbf{0}$
in the far field, we apply the divergence theorem to reduce the problem to the surface integral
Scaling the wave energy with the typical kinetic energy (
![]() $\unicode[STIX]{x1D70C}\unicode[STIX]{x1D706}^{5}T^{-2}$
), we use (B 2)–(B 6) to define the total energy dimensionless energy perturbation
$\unicode[STIX]{x1D70C}\unicode[STIX]{x1D706}^{5}T^{-2}$
), we use (B 2)–(B 6) to define the total energy dimensionless energy perturbation
where we define the inner product
Using the basis function expansions (3.7)–(3.8) and orthogonality, we can express the first inner product in terms of
![]() $a_{m}(t;k)$
,
$a_{m}(t;k)$
,
![]() $b_{m}(t;k)$
, and their time derivatives. The second inner product can be simplified via simple orthogonality. The third is easily simplified by recalling that the basis functions
$b_{m}(t;k)$
, and their time derivatives. The second inner product can be simplified via simple orthogonality. The third is easily simplified by recalling that the basis functions
![]() $\unicode[STIX]{x1D6F7}$
and
$\unicode[STIX]{x1D6F7}$
and
![]() $\unicode[STIX]{x1D6F9}$
are orthogonal eigenfunctions of Laplace’s equation.
$\unicode[STIX]{x1D6F9}$
are orthogonal eigenfunctions of Laplace’s equation.
Appendix C. Slow-walking analysis
We now state equations for
![]() $\unicode[STIX]{x1D6E4}_{2}$
,
$\unicode[STIX]{x1D6E4}_{2}$
,
![]() $a_{0}^{(2)}$
,
$a_{0}^{(2)}$
,
![]() $a_{2}^{(2)}$
and
$a_{2}^{(2)}$
and
![]() $a_{1}^{(3)}$
. The ODE inhomogeneities are
$a_{1}^{(3)}$
. The ODE inhomogeneities are
with jump condition inhomogeneities
and boundary inhomogeneities
To close the system, (5.9) requires
















