Hostname: page-component-8448b6f56d-jr42d Total loading time: 0 Render date: 2024-04-23T18:27:06.425Z Has data issue: false hasContentIssue false
  • English
  • Français

Fast Stokesian dynamics

Published online by Cambridge University Press:  17 September 2019

Andrew M. Fiore Open the ORCID record for Andrew M. Fiore [Opens in a new window]  and
James W. Swan
Andrew M. Fiore
Affiliation:
Department of Chemical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
James W. Swan*
Affiliation:
Department of Chemical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
*
†Email address for correspondence: jswan@mit.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We present a new method for large scale dynamic simulation of colloidal particles with hydrodynamic interactions and Brownian forces, which we call fast Stokesian dynamics (FSD). The approach for modelling the hydrodynamic interactions between particles is based on the Stokesian dynamics (SD) algorithm (J. Fluid Mech., vol. 448, 2001, pp. 115–146), which decomposes the interactions into near-field (short-ranged, pairwise additive and diverging) and far-field (long-ranged many-body) contributions. In FSD, the standard system of linear equations for SD is reformulated using a single saddle point matrix. We show that this reformulation is generalizable to a host of particular simulation methods enabling the self-consistent inclusion of a wide range of constraints, geometries and physics in the SD simulation scheme. Importantly for fast, large scale simulations, we show that the saddle point equation is solved very efficiently by iterative methods for which novel preconditioners are derived. In contrast to existing approaches to accelerating SD algorithms, the FSD algorithm avoids explicit inversion of ill-conditioned hydrodynamic operators without adequate preconditioning, which drastically reduces computation time. Furthermore, the FSD formulation is combined with advanced sampling techniques in order to rapidly generate the stochastic forces required for Brownian motion. Specifically, we adopt the standard approach of decomposing the stochastic forces into near-field and far-field parts. The near-field Brownian force is readily computed using an iterative Krylov subspace method, for which a novel preconditioner is developed, while the far-field Brownian force is efficiently computed by linearly transforming those forces into a fluctuating velocity field, computed easily using the positively split Ewald approach (J. Chem. Phys., vol. 146, 2017, 124116). The resultant effect of this field on the particle motion is determined through solution of a system of linear equations using the same saddle point matrix used for deterministic calculations. Thus, this calculation is also very efficient. Additionally, application of the saddle point formulation to develop high-resolution hydrodynamic models from constrained collections of particles (similar to the immersed boundary method) is demonstrated and the convergence of such models is discussed in detail. Finally, an optimized graphics processing unit implementation of FSD for mono-disperse spherical particles is used to demonstrated performance and accuracy of dynamic simulations of 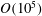$O(10^{5})$ particles, and an open source plugin for the HOOMD-blue suite of molecular dynamics software is included in the supplementary material.

JFM classification

Low-Reynolds-number flows: Stokesian dynamics
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 878 , 10 November 2019 , pp. 544 - 597
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramowitz, M. & Stegun, I. A. 1965 Handbook of Mathematical Function: with Formulas, Graphs and Mathematical Tables. Dover.Google Scholar
Allen, M. P. & Tildesley, D. J. 1989 Computer Simulation of Liquids. Oxford University Press.Google Scholar
Anderson, J. A., Lorenz, C. D. & Travesset, A. 2008 General purpose molecular dynamics simulations fully implemented on graphics processing units. J. Comput. Phys. 227 (10), 5342–5359.Google Scholar
Balboa Usabiaga, F., Kallemov, B., Delmotte, B., Bhalla, A., Griffith, B. & Donev, A. 2016 Hydrodynamics of suspensions of passive and active rigid particles: a rigid multiblob approach. Commun. Appl. Maths Comput. Sci. 11 (2), 217–296.Google Scholar
Banchio, A. J. & Brady, J. F. 2003 Accelerated Stokesian dynamics: Brownian motion. J. Chem. Phys. 118 (22), 10323–10332.Google Scholar
Benzi, M., Golub, G. H. & Liesen, J. 2005 Numerical solution of saddle point problems. Acta Numerica 14, 1–137.Google Scholar
Brady, J. F. 1993 Brownian motion, hydrodynamics, and the osmotic pressure. J. Chem. Phys. 98 (4), 3335–3341.Google Scholar
Brady, J. F. & Bossis, G. 1988 Stokesian dynamics. Annu. Rev. Fluid Mech. 20, 111–157.Google Scholar
Brady, J. F., Phillips, R. J., Lester, J. C. & Bossis, G. 1988 Dynamic simulation of hydrodynamically interacting suspensions. J. Fluid Mech. 195, 257–280.Google Scholar
Burkardt, J.2011 RCM Reverse Cuthill McKee Ordering C++ Library. https://people.sc.fsu.edu/∼jburkardt/f_src/rcm/rcm.html.Google Scholar
Chow, E. & Saad, Y. 2014 Preconditioned Krylov subspace methods for sampling multivariate Gaussian distributions. SIAM J. Sci. Comput. 36 (2), A588–A608.Google Scholar
Cichocki, B., Ekiel-Jeżewska, M. L. & Wajnryb, E. 1999 Lubrication corrections for three-particle contribution to short-time self-diffusion coefficients in colloidal dispersions. J. Chem. Phys. 111 (7), 3265–3273.Google Scholar
Cichocki, B., Felderhof, B. U., Hinsen, K., Wajnryb, E. & Bl/awzdziewicz, J. 1994 Friction and mobility of many spheres in Stokes flow. J. Chem. Phys. 100 (5), 3780–3790.Google Scholar
Cuthill, E. & McKee, J. 1969 Reducing the bandwidth of sparse symmetric matrices. In Proceedings of the 1969 24th National Conference, pp. 157–172. ACM.Google Scholar
Dalton, S., Bell, N., Olson, L. & Garland, M.2014 Cusp: generic parallel algorithms for sparse matrix and graph computations. Version 0.5.0.Google Scholar
Darden, T., York, D. & Pedersen, L. 1993 Particle mesh Ewald: an Nlog(N) method for Ewald sums in large systems. J. Chem. Phys. 98 (12), 10089–10092.Google Scholar
Delmotte, B. & Keaveny, E. E. 2015 Simulating Brownian suspensions with fluctuating hydrodynamics. J. Chem. Phys. 143 (24), 244109.Google Scholar
Delong, S., Balboa Usabiaga, F. & Donev, A. 2015 Brownian dynamics of confined rigid bodies. J. Chem. Phys. 143 (14), 144107.Google Scholar
Delong, S., Usabiaga, F. B., Delgado-Buscalioni, R., Griffith, B. E. & Donev, A. 2014 Brownian dynamics without Green’s functions. J. Chem. Phys. 140 (13), 134110.Google Scholar
Ermak, D. L. & McCammon, J. A. 1978 Brownian dynamics with hydrodynamic interactions. J. Chem. Phys. 69 (4), 1352–1360.Google Scholar
Ewald, P. P. 1921 Die berechnung optischer und elektrostatischer gitterpotentiale. Ann. Phys. 369 (3), 253–287.Google Scholar
Fiore, A. M. & Swan, J. W. 2018 Rapid sampling of stochastic displacements in Brownian dynamics simulations with stresslet constraints. J. Chem. Phys. 148 (4), 044114.Google Scholar
Fiore, A. M., Usabiaga, F. B., Donev, A. & Swan, J. W. 2017 Rapid sampling of stochastic displacements in Brownian dynamics simulations. J. Chem. Phys. 146 (12), 124116.Google Scholar
Fiore, A. M., Wang, G. & Swan, J. W. 2018 From hindered to promoted settling in dispersions of attractive colloids: simulation, modeling, and application to macromolecular characterization. Phys. Rev. Fluids 3 (6), 063302.Google Scholar
Fixman, M. 1986 Construction of Langevin forces in the simulation of hydrodynamic interaction. Macromolecules 19 (4), 1204–1207.Google Scholar
George, A. & Liu, J. 1981 Computer Solution of Large Sparse Positive Definite Systems. Prentice-Hall.Google Scholar
Glaser, J., Nguyen, T. D., Anderson, J. A., Lui, P., Spiga, F., Millan, J. A., Morse, D. C. & Glotzer, S. C. 2015 Strong scaling of general-purpose molecular dynamics simulations on GPUs. Comput. Phys. Commun. 192, 97–107.Google Scholar
Goldberg, M. 1937 A class of multi-symmetric polyhedra. Tohoku Math. J. (1) 43, 104–108.Google Scholar
Gompper, G., Ihle, T., Kroll, D. M. & Winkler, R. G. 2009 Multi-particle collision dynamics: a particle-based mesoscale simulation approach to the hydrodynamics of complex fluids. In Advanced Computer Simulation Approaches for Soft Matter Sciences III, pp. 1–87. Springer.Google Scholar
Griffith, B. E. 2009 An accurate and efficient method for the incompressible Navier–Stokes equations using the projection method as a preconditioner. J. Comput. Phys. 228 (20), 7565–7595.Google Scholar
Guo, X., Liu, X., Xu, P., Du, Z. & Chow, E. 2015 Efficient particle-mesh spreading on GPUs. Proc. Comput. Sci. 51, 120–129.Google Scholar
Hasimoto, H. 1959 On the periodic fundamental solutions of the Stokes equations and their application to viscous flow past a cubic array of spheres. J. Fluid Mech. 5, 317–328.Google Scholar
Hinch, E. J. 1975 Application of the Langevin equation to fluid suspensions. J. Fluid Mech. 72 (3), 499–511.Google Scholar
Hoogerbrugge, P. J. & Koelman, J. M. V. A. 1992 Simulating microscopic hydrodynamic phenomena with dissipative particle dynamics. Europhys. Lett. 19 (3), 155–160.Google Scholar
Ichiki, K. 2002 Improvement of the Stokesian dynamics method for systems with a finite number of particles. J. Fluid Mech. 452, 231–262.Google Scholar
Jeffrey, D.1992a Programs for Stokes resistance functions. https://www.uwo.ca/apmaths/faculty/jeffrey/research/Resistance.html.Google Scholar
Jeffrey, D. J. 1992b The calculation of the low Reynolds number resistance functions for two unequal spheres. Phys. Fluids A 4 (1), 16–29.Google Scholar
Jeffrey, D. J. & Onishi, Y. 1984 Calculation of the resistance and mobility functions for two unequal rigid spheres in low-Reynolds-number flow. J. Fluid Mech. 139, 261–290.Google Scholar
Keaveny, E. E. 2014 Fluctuating force-coupling method for simulations of colloidal suspensions. J. Comput. Phys. 269, 61–79.Google Scholar
Kim, S. & Karrila, S. J. 2005 Microhydrodynamics: Principles and Selected Applications. Dover.Google Scholar
Kubo, R. 1966 The fluctuation–dissipation theorem. Rep. Prog. Phys. 29 (1), 255–284.Google Scholar
Ladd, A. J. C. 1990 Hydrodynamic transport coefficients of random dispersions of hard spheres. J. Chem. Phys. 93 (5), 3484–3494.Google Scholar
Ladd, A. J. C., Colvin, M. E. & Frenkel, D. 1988 Application of lattice-gas cellular automata to the Brownian motion of solids in suspension. Phys. Rev. Lett. 60 (11), 975–978.Google Scholar
Ladyzhenskaya, O. A. & Silverman, R. A. 1969 The Mathematical Theory of Viscous Incompressible Flow, vol. 12. Gordon & Breach.Google Scholar
Lefebvre-Lepot, A., Merlet, B. & Nguyen, T. N. 2015 An accurate method to include lubrication forces in numerical simulations of dense Stokesian suspensions. J. Fluid Mech. 769, 369–386.Google Scholar
Lindbo, D. & Tornberg, A.-K. 2010 Spectrally accurate fast summation for periodic Stokes potentials. J. Comput. Phys. 229 (23), 8994–9010.Google Scholar
Lomholt, S. & Maxey, M. R. 2003 Force-coupling method for particulate two-phase flow: Stokes flow. J. Comput. Phys. 184 (2), 381–405.Google Scholar
Meng, Q. & Higdon, J. J. L. 2008a Large scale dynamic simulation of plate-like particle suspensions. Part I. Non-Brownian simulation. J. Rheol. 52 (1), 1–36.Google Scholar
Meng, Q. & Higdon, J. J. L. 2008b Large scale dynamic simulation of plate-like particle suspensions. Part II. Brownian simulation. J. Rheol. 52 (1), 37–65.Google Scholar
Mizerski, K. A., Wajnryb, E., Zuk, P. J. & Szymczak, P. 2014 The Rotne–Prager–Yamakawa approximation for periodic systems in a shear flow. J. Chem. Phys. 140 (18), 184103.Google Scholar
NVIDIA2018 CUDA Toolkit Documentation.Google Scholar
Regnaut, C. & Ravey, J. C. 1989 Application of the adhesive sphere model to the structure of colloidal suspensions. J. Chem. Phys. 91 (2), 1211–1221.Google Scholar
Regnaut, C. & Ravey, J. C. 1990 Erratum: application of the adhesive sphere model to the structure of colloidal suspensions [J. Chem. Phys. 9 1, 1211 (1989)]. J. Chem. Phys. 92 (5), 3250–3250.Google Scholar
Rotne, J. & Prager, S. 1969 Variational treatment of hydrodynamic interaction in polymers. J. Chem. Phys. 50 (11), 4831–4837.Google Scholar
Roux, J.-N. 1992 Brownian particles at different times scales: a new derivation of the Smoluchowski equation. Physica A 188 (4), 526–552.Google Scholar
Saad, Y. & Schultz, M. H. 1986 GMRES: a generalized minimal residual algorithm for solving nonsymmetric linear systems. SIAM J. Sci. Stat. Comput. 7 (3), 856–869.Google Scholar
Saintillan, D., Darve, E. & Shaqfeh, E. S. G. 2005 A smooth particle-mesh Ewald algorithm for Stokes suspension simulations: the sedimentation of fibers. Phys. Fluids 17 (3), 033301.Google Scholar
Sierou, A. & Brady, J. F. 2001 Accelerated Stokesian dynamics simulations. J. Fluid Mech. 448, 115–146.Google Scholar
Sprinkle, B., Balboa Usabiaga, F., Patankar, N. A. & Donev, A. 2017 Large scale Brownian dynamics of confined suspensions of rigid particles. J. Chem. Phys. 147 (24), 244103.Google Scholar
Swan, J. W. & Wang, G. 2016 Rapid calculation of hydrodynamic and transport properties in concentrated solutions of colloidal particles and macromolecules. Phys. Fluids 28 (1), 011902.Google Scholar
Tornberg, A.-K. & Greengard, L. 2008 A fast multipole method for the three-dimensional Stokes equations. J. Comput. Phys. 227 (3), 1613–1619.Google Scholar
Viera, M. N.2002 Large scale simulations of Brownian suspensions. PhD thesis, University of Illinois at Urbana-Champaign.Google Scholar
Wang, G., Fiore, A. M. & Swan, J. W. 2019 On the viscosity of adhesive hard sphere dispersions: critical scaling and the role of rigid contacts. J. Rheol. 63 (2), 229–245.Google Scholar
Wang, M. & Brady, J. F. 2016 Spectral Ewald acceleration of Stokesian dynamics for polydisperse suspensions. J. Comput. Phys. 306, 443–477.Google Scholar
Yeo, K. & Maxey, M. R. 2010 Simulation of concentrated suspensions using the force-coupling method. J. Comput. Phys. 229 (6), 2401–2421.Google Scholar
Supplementary material: File

Fiore and Swan supplementary material

Fiore and Swan supplementary material

Download Fiore and Swan supplementary material(File)
File 918.7 KB