Article contents
Finite Reynolds number effect on the scaling range behaviour of turbulent longitudinal velocity structure functions
Published online by Cambridge University Press: 05 May 2017
Abstract
The effect of large-scale forcing on the second- and third-order longitudinal velocity structure functions, evaluated at the Taylor microscale 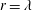 $r=\unicode[STIX]{x1D706}$ , is assessed in various turbulent flows at small to moderate values of the Taylor microscale Reynolds number
$r=\unicode[STIX]{x1D706}$ , is assessed in various turbulent flows at small to moderate values of the Taylor microscale Reynolds number 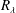 $R_{\unicode[STIX]{x1D706}}$ . It is found that the contribution of the large-scale terms to the scale by scale energy budget differs from flow to flow. For a fixed
$R_{\unicode[STIX]{x1D706}}$ . It is found that the contribution of the large-scale terms to the scale by scale energy budget differs from flow to flow. For a fixed 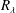 $R_{\unicode[STIX]{x1D706}}$ , this contribution is largest on the centreline of a fully developed channel flow but smallest for stationary forced periodic box turbulence. For decaying-type flows, the contribution lies between the previous two cases. Because of the difference in the large-scale term between flows, the third-order longitudinal velocity structure function at
$R_{\unicode[STIX]{x1D706}}$ , this contribution is largest on the centreline of a fully developed channel flow but smallest for stationary forced periodic box turbulence. For decaying-type flows, the contribution lies between the previous two cases. Because of the difference in the large-scale term between flows, the third-order longitudinal velocity structure function at 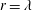 $r=\unicode[STIX]{x1D706}$ differs from flow to flow at small to moderate
$r=\unicode[STIX]{x1D706}$ differs from flow to flow at small to moderate 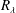 $R_{\unicode[STIX]{x1D706}}$ . The effect on the second-order velocity structure functions appears to be negligible. More importantly, the effect of
$R_{\unicode[STIX]{x1D706}}$ . The effect on the second-order velocity structure functions appears to be negligible. More importantly, the effect of 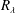 $R_{\unicode[STIX]{x1D706}}$ on the scaling range exponent of the longitudinal velocity structure function is assessedusing measurements of the streamwise velocity fluctuation
$R_{\unicode[STIX]{x1D706}}$ on the scaling range exponent of the longitudinal velocity structure function is assessedusing measurements of the streamwise velocity fluctuation  $u$ , with
$u$ , with 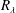 $R_{\unicode[STIX]{x1D706}}$ in the range 500–1100, on the axis of a plane jet. It is found that the magnitude of the exponent increases as
$R_{\unicode[STIX]{x1D706}}$ in the range 500–1100, on the axis of a plane jet. It is found that the magnitude of the exponent increases as 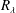 $R_{\unicode[STIX]{x1D706}}$ increases and the rate of increase depends on the order
$R_{\unicode[STIX]{x1D706}}$ increases and the rate of increase depends on the order  $n$ . The trend of published structure function data on the axes of an axisymmetric jet and a two-dimensional wake confirms this dependence. For a fixed
$n$ . The trend of published structure function data on the axes of an axisymmetric jet and a two-dimensional wake confirms this dependence. For a fixed 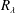 $R_{\unicode[STIX]{x1D706}}$ , the exponent can vary from flow to flow and for a given flow, the larger
$R_{\unicode[STIX]{x1D706}}$ , the exponent can vary from flow to flow and for a given flow, the larger 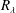 $R_{\unicode[STIX]{x1D706}}$ is, the closer the exponent is to the value predicted by Kolmogorov (Dokl. Akad. Nauk SSSR, vol. 30, 1941a, pp. 299–303) (hereafter K41). The major conclusion is that the finite Reynolds number effect, which depends on the flow, needs to be properly accounted for before determining whether corrections to K41, arising from the intermittency of the energy dissipation rate, are needed. We further point out that it is imprudent, if not incorrect, to associate the finite Reynolds number effect with a consequence of the modified similarity hypothesis introduced by Kolmogorov (J. Fluid Mech., vol. 13, 1962, pp. 82–85) (K62); we contend that this association has misled the vast majority of post K62 investigations of the consequences of K62.
$R_{\unicode[STIX]{x1D706}}$ is, the closer the exponent is to the value predicted by Kolmogorov (Dokl. Akad. Nauk SSSR, vol. 30, 1941a, pp. 299–303) (hereafter K41). The major conclusion is that the finite Reynolds number effect, which depends on the flow, needs to be properly accounted for before determining whether corrections to K41, arising from the intermittency of the energy dissipation rate, are needed. We further point out that it is imprudent, if not incorrect, to associate the finite Reynolds number effect with a consequence of the modified similarity hypothesis introduced by Kolmogorov (J. Fluid Mech., vol. 13, 1962, pp. 82–85) (K62); we contend that this association has misled the vast majority of post K62 investigations of the consequences of K62.
Information
- Type
- Papers
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 27
- Cited by


