Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Zhao, Guang
2014.
Aerodynamics Study of Flow Past Two Tandem Bluff Bodies at Low Reynolds Number.
Applied Mechanics and Materials,
Vol. 668-669,
Issue. ,
p.
138.
Carini, M.
Auteri, F.
and
Giannetti, F.
2015.
Centre-manifold reduction of bifurcating flows.
Journal of Fluid Mechanics,
Vol. 767,
Issue. ,
p.
109.
Citro, V.
Giannetti, F.
Luchini, P.
and
Auteri, F.
2015.
Global stability and sensitivity analysis of boundary-layer flows past a hemispherical roughness element.
Physics of Fluids,
Vol. 27,
Issue. 8,
Camarri, Simone
2015.
Flow control design inspired by linear stability analysis.
Acta Mechanica,
Vol. 226,
Issue. 4,
p.
979.
Chen, Weilin
Ji, Chunning
Wang, Rui
Xu, Dong
and
Campbell, Jordan
2015.
Flow-induced vibrations of two side-by-side circular cylinders: Asymmetric vibration, symmetry hysteresis and near-wake patterns.
Ocean Engineering,
Vol. 110,
Issue. ,
p.
244.
Carini, M.
Auteri, F.
and
Giannetti, F.
2015.
Secondary instabilities of the in-phase synchronized wakes past two circular cylinders in side-by-side arrangement.
Journal of Fluids and Structures,
Vol. 53,
Issue. ,
p.
70.
Peng, Yih Ferng
and
Sau, Amalendu
2015.
Transitional hysteresis loop and coexistence of synchronized shedding in coupled wakes.
Physics of Fluids,
Vol. 27,
Issue. 7,
Carini, M.
Airiau, C.
Debien, A.
Léon, O.
and
Pralits, J. O.
2017.
Global stability and control of the confined turbulent flow past a thick flat plate.
Physics of Fluids,
Vol. 29,
Issue. 2,
Canton, J.
Auteri, F.
and
Carini, M.
2017.
Linear global stability of two incompressible coaxial jets.
Journal of Fluid Mechanics,
Vol. 824,
Issue. ,
p.
886.
Dare, Tyler
Berger, Zachary P.
Meehan, Michael
and
O'Connor, Jacqueline A.
2018.
Cluster-based Reduced-Order Modeling to Capture Intermittent Dynamics of Interacting Wakes.
Meehan, M.
Tyagi, A.
and
O’Connor, J.
2018.
Flow dynamics in a variable-spacing, three bluff-body flowfield.
Physics of Fluids,
Vol. 30,
Issue. 2,
Zafar, Farhan
and
Alam, Md. Mahbub
2018.
A low Reynolds number flow and heat transfer topology of a cylinder in a wake.
Physics of Fluids,
Vol. 30,
Issue. 8,
Dare, Tyler P.
Berger, Zachary P.
Meehan, Michael
and
O’Connor, Jacqueline
2019.
Cluster-Based Reduced-Order Modeling to Capture Intermittent Dynamics of Interacting Wakes.
AIAA Journal,
Vol. 57,
Issue. 7,
p.
2819.
Magri, Luca
2019.
Adjoint Methods as Design Tools in Thermoacoustics.
Applied Mechanics Reviews,
Vol. 71,
Issue. 2,
Sooraj, P.
Khan, Majid Hassan
Sharma, Atul
and
Agrawal, Amit
2019.
Wake analysis and regimes for flow around three side-by-side cylinders.
Experimental Thermal and Fluid Science,
Vol. 104,
Issue. ,
p.
76.
Auteri, F.
de Tullio, M. D.
Guermond, J.-L.
Montagnani, D.
and
Konghar, P. D.
2019.
Direct and Large-Eddy Simulation XI.
Vol. 25,
Issue. ,
p.
23.
Gao, Yangyang
Liu, Cai
Zhao, Ming
Wang, Lizhong
and
Zhu, Ronghua
2020.
Experimental Investigation on Flow Past Two and Three Side-by-Side Inclined Cylinders.
Journal of Fluids Engineering,
Vol. 142,
Issue. 1,
Chen, Weilin
Ji, Chunning
Alam, Md. Mahbub
Williams, John
and
Xu, Dong
2020.
Numerical simulations of flow past three circular cylinders in equilateral-triangular arrangements.
Journal of Fluid Mechanics,
Vol. 891,
Issue. ,
Furquan, Mohd
and
Mittal, Sanjay
2021.
Flow-induced vibration of filaments attached to two side-by-side cylinders.
Physics of Fluids,
Vol. 33,
Issue. 6,
Yan, Yuhao
Ji, Chunning
and
Srinil, Narakorn
2021.
On wake modulation and interaction features of a pair of dual-step circular cylinders in side-by-side arrangements.
Physics of Fluids,
Vol. 33,
Issue. 9,
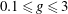 $0.1\leq g\leq 3$ and
$0.1\leq g\leq 3$ and 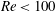 $\mathit{Re}<100$ , with
$\mathit{Re}<100$ , with 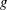 $g$ being the non-dimensional gap spacing between the surfaces of the two cylinders and
$g$ being the non-dimensional gap spacing between the surfaces of the two cylinders and 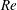 $\mathit{Re}$ the Reynolds number. A comprehensive, global stability analysis of the symmetric base flow is carried out, indicating that three harmonic modes and one steady antisymmetric mode become unstable at different values of
$\mathit{Re}$ the Reynolds number. A comprehensive, global stability analysis of the symmetric base flow is carried out, indicating that three harmonic modes and one steady antisymmetric mode become unstable at different values of 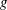 $g$ and
$g$ and 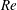 $\mathit{Re}$ . These modes are known to promote distinct flow regimes at increasing values of
$\mathit{Re}$ . These modes are known to promote distinct flow regimes at increasing values of 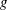 $g$ : single bluff-body, asymmetric, in-phase and antiphase synchronized vortex shedding. For each mode, the inherent structural sensitivity is examined in order to identify the core region of the related instability mechanism. In addition, by exploiting the structural sensitivity analysis to base flow modifications, a passive control strategy is proposed for the simultaneous suppression of the two synchronized shedding modes using two small secondary cylinders. Its effectiveness is then validated a posteriori by means of direct numerical simulations.
$g$ : single bluff-body, asymmetric, in-phase and antiphase synchronized vortex shedding. For each mode, the inherent structural sensitivity is examined in order to identify the core region of the related instability mechanism. In addition, by exploiting the structural sensitivity analysis to base flow modifications, a passive control strategy is proposed for the simultaneous suppression of the two synchronized shedding modes using two small secondary cylinders. Its effectiveness is then validated a posteriori by means of direct numerical simulations.
