Hostname: page-component-8448b6f56d-c4f8m Total loading time: 0 Render date: 2024-04-25T05:28:05.877Z Has data issue: false hasContentIssue false
  • English
  • Français

From three-dimensional to quasi-two-dimensional: transient growth in magnetohydrodynamic duct flows

Published online by Cambridge University Press:  19 December 2018

Oliver G. W. Cassells Open the ORCID record for Oliver G. W. Cassells [Opens in a new window] ,
Tony Vo ,
Alban Pothérat Open the ORCID record for Alban Pothérat [Opens in a new window]  and
Gregory J. Sheard Open the ORCID record for Gregory J. Sheard [Opens in a new window]
Oliver G. W. Cassells
Affiliation:
Department of Mechanical and Aerospace Engineering, Monash University, Victoria 3800, Australia
Tony Vo
Affiliation:
Department of Mechanical and Aerospace Engineering, Monash University, Victoria 3800, Australia
Alban Pothérat
Affiliation:
Fluid and Complex Systems Research Centre, Coventry University, Coventry CV15FB, UK
Gregory J. Sheard*
Affiliation:
Department of Mechanical and Aerospace Engineering, Monash University, Victoria 3800, Australia
*
†Email address for correspondence: greg.sheard@monash.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

This study seeks to elucidate the linear transient growth mechanisms in a uniform duct with square cross-section applicable to flows of electrically conducting fluids under the influence of an external magnetic field. A particular focus is given to the question of whether at high magnetic fields purely two-dimensional mechanisms exist, and whether these can be described by a computationally inexpensive quasi-two-dimensional model. 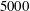Two Reynolds numbers of $5000$ and 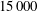$15\,000$ and an extensive range of Hartmann numbers 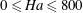$0\leqslant \mathit{Ha}\leqslant 800$ were investigated. Three broad regimes are identified in which optimal mode topology and non-modal growth mechanisms are distinct. These regimes, corresponding to low, moderate and high magnetic field strengths, are found to be governed by the independent parameters; Hartmann number, Reynolds number based on the Hartmann layer thickness 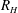$R_{H}$ and Reynolds number built upon the Shercliff layer thickness 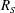$R_{S}$, respectively. Transition between regimes respectively occurs at 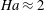$\mathit{Ha}\approx 2$ and no lower than $R_{H}\approx 33.\dot{3}$. Notably for the high Hartmann number regime, quasi-two-dimensional magnetohydrodynamic models are shown to be excellent predictors of not only transient growth magnitudes, but also the fundamental growth mechanisms of linear disturbances. This paves the way for a precise analysis of transition to quasi-two-dimensional turbulence at much higher Hartmann numbers than is currently achievable.

JFM classification

Instability: Instability MHD and Electrohydrodynamics: MHD and Electrohydrodynamics
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 861 , 25 February 2019 , pp. 382 - 406
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Airiau, C. & Castets, M. 2004 On the amplification of small disturbances in a channel flow with a normal magnetic field. Phys. Fluids 16 (8), 2991–3005.Google Scholar
Alemany, A., Moreau, R., Sulem, P. & Frisch, U. 1979 Influence of an external magnetic field on homogeneous MHD turbulence. J. Méc. 18 (2), 277–313.Google Scholar
Baker, N. T., Pothérat, A., Davoust, L. & Debray, F. M. C. 2018 Inverse and direct energy cascades in three-dimensional magnetohydrodynamic turbulence at low magnetic Reynolds number. Phys. Rev. Lett. 120, 224502.Google Scholar
Barkley, D., Blackburn, H. & Sherwin, S. 2008 Direct optimal growth analysis for timesteppers. Intl J. Numer. Meth. Fluids 231, 1–20.Google Scholar
Biau, D. & Bottaro, A. 2004 Transient growth and minimal defects: two possible initial paths of transition to turbulence in plane shear flows. Phys. Fluids 16 (10), 3515–3529.Google Scholar
Biau, D., Soueid, H. & Bottaro, A. 2008 Transition to turbulence in duct flow. J. Fluid Mech. 596, 133–142.Google Scholar
Blackburn, H. M., Sherwin, S. J. & Barkley, D. 2008 Convective instability and transient growth in steady and pulsatile stenotic flows. J. Fluid Mech. 607, 267–277.Google Scholar
Böberg, L. & Brösa, U. 1988 Onset of turbulence in a pipe. Z. Naturforsch. A 43 (8–9), 697–726.Google Scholar
Cassells, O. G. W., Hussam, W. K. & Sheard, G. J. 2016 Heat transfer enhancement using rectangular vortex promoters in confined quasi-two-dimensional magnetohydrodynamic flows. Intl J. Heat Mass Transfer 93, 186–199.Google Scholar
Dousset, V. & Pothérat, A. 2008 Numerical simulations of a cylinder wake under a strong axial magnetic field. Phys. Fluids 20, 017104.Google Scholar
Frisch, U. 1995 Turbulence: The Legacy of A. N. Kolmogorov. Cambridge University Press.Google Scholar
Gerard-Varet, D. 2002 Amplification of small perturbations in a Hartmann layer. Phys. Fluids 14 (4), 1458–1467.Google Scholar
Greenspan, H. 1968 The Theory of Rotating Fluids. Cambridge University Press.Google Scholar
Hamid, A. H., Hussam, W. K., Pothérat, A. & Sheard, G. J. 2015 Spatial evolution of a quasi-two-dimensional Kármán vortex street subjected to a strong uniform magnetic field. Phys. Fluids 27 (5), 053602.Google Scholar
Hamid, A. H. A., Hussam, W. K. & Sheard, G. J. 2016 Combining an obstacle and electrically driven vortices to enhance heat transfer in a quasi-two-dimensional MHD duct flow. J. Fluid Mech. 792, 364–396.Google Scholar
Hunt, J. C. R. & Stewartson, K. 1965 Magnetohydrodynamic flow in rectangular ducts. Part II. J. Fluid Mech. 23 (3), 563–581.Google Scholar
Hussam, W. K. & Sheard, G. J. 2013 Heat transfer in a high Hartmann number MHD duct flow with a circular cylinder placed near the heated side-wall. Intl J. Heat Mass Transfer 67, 944–954.Google Scholar
Hussam, W. K., Thompson, M. C. & Sheard, G. J. 2012a Enhancing heat transfer in a high Hartmann number magnetohydrodynamic channel flow via torsional oscillation of a cylindrical obstacle. Phys. Fluids 24, 113601.Google Scholar
Hussam, W. K., Thompson, M. C. & Sheard, G. J. 2012b Optimal transient disturbances behind a circular cylinder in a quasi-two-dimensional magnetohydrodynamic duct flow. Phys. Fluids 24, 024105.Google Scholar
Kanaris, N., Albets, X., Grigoriadis, D. & Kassinos, S. 2013 Three-dimensional numerical simulations of magnetohydrodynamic flow around a confined circular cylinder under low, moderate, and strong magnetic fields. Phys. Fluids 25, 074102.Google Scholar
Karniadakis, G. E., Israeli, M. & Orszag, S. A. 1991 High-order splitting methods for the incompressible Navier–Stokes equations. J. Comput. Phys. 97 (2), 414–443.Google Scholar
Klein, R. & Pothérat, A. 2010 Appearance of three dimensionality in wall-bounded MHD flows. Phys. Rev. Lett. 104 (3), 034502.Google Scholar
Krasnov, D., Zienicke, E., Zikanov, O., Boeck, T. & Thess, A. 2004 Numerical study of the instability of the Hartmann layer. J. Fluid Mech. 504, 183–211.Google Scholar
Krasnov, D., Zikanov, O. & Boeck, T. 2012 Numerical study of magnetohydrodynamic duct flow at high Reynolds and Hartmann numbers. J. Fluid Mech. 704, 421.Google Scholar
Krasnov, D., Zikanov, O., Rossi, M. & Boeck, T. 2010 Optimal linear growth in magnetohydrodynamic duct flow. J. Fluid Mech. 653, 273–299.Google Scholar
Landahl, M. 1980 A note on an algebraic instability of inviscid parallel shear flows. J. Fluid Mech. 98 (2), 243–251.Google Scholar
Lehoucq, R., Sorensen, D. & Yang, C.1998 ARPACK users’ guide. Society for Industrial and Applied Mathematics. http://epubs.siam.org/doi/pdf/10.1137/1.9780898719628.Google Scholar
Leigh, M. A., Tsai, T. & Sheard, G. J. 2016 Probing horizontal convection instability via perturbation of the forcing boundary layer using a synthetic jet. Intl J. Therm. Sci. 110, 251–260.Google Scholar
Moresco, P. & Alboussiere, T. 2004 Experimental study of the instability of the Hartmann layer. J. Fluid Mech. 504, 167–181.Google Scholar
Mück, B., Günther, C., Müller, U. & Bühler, L. 2000 Three-dimensional MHD flows in rectangular ducts with internal obstacles. J. Fluid Mech. 418, 265–295.Google Scholar
Müller, U. & Bühler, L. 2001 Magnetofluiddynamics in Channels and Containers, 1st edn. Springer.Google Scholar
Ng, Z. Y., Vo, T., Hussam, W. K. & Sheard, G. J. 2016 Two-dimensional wake dynamics behind cylinders with triangular cross-section under incidence angle variation. J. Fluids Struct. 63, 302–324.Google Scholar
Ni, M.-J., Munipalli, R., Morley, N. B., Huang, P. & Abdou, M. A. 2007 A current density conservative scheme for incompressible MHD flows at a low magnetic Reynolds number. Part I. On a rectangular collocated grid system. J. Comput. Phys. 227 (1), 174–204.Google Scholar
Ó Náraigh, L. 2015 Global modes in nonlinear non-normal evolutionary models: exact solutions, perturbation theory, direct numerical simulation, and chaos. Physica D 309, 20–36.Google Scholar
Orr, W. M. 1907 The stability or instability of the steady motions of a perfect liquid and of a viscous liquid. Part II. A viscous liquid. Proceedings of the Royal Irish Academy, Section A: Mathematical and Physical Sciences 27, 69–138.Google Scholar
Paret, J., Marteau, D., Paireau, O. & Tabeling, P. 1997 Are flows electromagnetically forced in thin stratified layers two dimensional? Phys. Fluids 9 (10), 3102–3104.Google Scholar
Pothérat, A. 2007 Quasi-two-dimensional perturbations in duct flows under transverse magnetic field. Phys. Fluids 19, 074104.Google Scholar
Pothérat, A. 2012 Three-dimensionality in quasi-two-dimensional flows: recirculations and Barrel effects. Europhys. Lett. 98 (6), 64003.Google Scholar
Pothérat, A. & Klein, R. 2014 Why, how and when MHD turbulence at low Rm becomes three-dimensional. J. Fluid Mech. 761, 168–205.Google Scholar
Pothérat, A., Sommeria, J. & Moreau, R. 2000 An effective two-dimensional model for MHD flows with transverse magnetic field. J. Fluid Mech. 424, 75–100.Google Scholar
Reddy, S. C. & Henningson, D. S. 1993 Energy growth in viscous channel flows. J. Fluid Mech. 252, 209–238.Google Scholar
Reshotko, E. 2001 Transient growth: a factor in bypass transition. Phys. Fluids 13 (5), 1067–1075.Google Scholar
Sapardi, A. M., Hussam, W. K., Pothérat, A. & Sheard, G. J. 2017 Linear stability of confined flow around a 180-degree sharp bend. J. Fluid Mech. 822, 813–847.Google Scholar
Schmid, P. J. & Henningson, D. S. 2001 Stability and Transition in Shear Flows. Springer.Google Scholar
Sheard, G. J., Hussam, W. K. & Tsai, T. 2016 Linear stability and energetics of rotating radial horizontal convection. J. Fluid Mech. 795, 1–35.Google Scholar
Smolentsev, S. & Moreau, R. 2007 One-equation model for quasi-two-dimensional turbulent magnetohydrodynamic flows. Phys. Fluids 19 (7), 078101.Google Scholar
Smolentsev, S., Wong, C., Malang, S., Dagher, M. & Abdou, M. 2010 MHD considerations for the DCLL inboard blanket and access ducts. Fusion Engng Des. 85 (7), 1007–1011.Google Scholar
Sommeria, J. & Moreau, R. 1982 Why, how, and when, MHD turbulence becomes two-dimensional. J. Fluid Mech. 118, 507–518.Google Scholar
Trefethen, L. N., Trefethen, A. E., Reddy, S. C. & Driscoll, T. A. 1993 Hydrodynamic stability without eigenvalues. Science 261 (5121), 578–584.Google Scholar
Tsai, T., Hussam, W. K., Fouras, A. & Sheard, G. J. 2016 The origin of instability in enclosed horizontally driven convection. Intl J. Heat Mass Transfer 94, 509–515.Google Scholar
Vo, T., Montabone, L., Read, P. L. & Sheard, G. J. 2015 Non-axisymmetric flows in a differential-disk rotating system. J. Fluid Mech. 775, 349–386.Google Scholar
Vo, T., Pothérat, A. & Sheard, G. J. 2017 Linear stability of horizontal, laminar fully developed, quasi-two-dimensional liquid metal duct flow under a transverse magnetic field and heated from below. Phys. Rev. Fluids 2 (3), 033902.Google Scholar
Waleffe, F. 1997 On a self-sustaining process in shear flows. Phys. Fluids 9 (4), 883–900.Google Scholar
Zienicke, E. & Krasnov, D. 2005 Parametric study of streak breakdown mechanism in Hartmann flow. Phys. Fluids 17 (11), 114101.Google Scholar