1 Introduction
Accurate modelling of the flow of gases in micro- and nanoscale environments is known to be key to understanding and optimising numerous industrial and environmental processes. For example, in micro-electro-mechanical systems (Judy Reference Judy2001), detailed flow information is required to improve the design and functionality of devices in computational hardware through to biomedical analysis. In particulate flows, serious impacts on human health can arise due to ingesting emissions from industry, so that calculation of the flow around microparticles is of paramount importance to predicting how these emissions will spread (Valavanidis, Fiotakis & Vlachogianni Reference Valavanidis, Fiotakis and Vlachogianni2008). Efficient modelling of these gas microflows is complicated, as the classical fluid mechanical formulation, based on the Navier–Stokes–Fourier (NSF) equations, fails to accurately describe them (Cercignani Reference Cercignani2006).
The NSF equations become increasingly inaccurate as the Knudsen number,
$\mathit{Kn}^{\prime }=\unicode[STIX]{x1D706}/L$
, based on the ratio of the gas mean free path
$\unicode[STIX]{x1D706}$
to a characteristic length scale of the process
$L$
, becomes increasingly large. For
$\mathit{Kn}^{\prime }\gtrsim 0.01$
, the NSF equations often fail to even produce the correct qualitative picture, with the bulk flow deformed by effects such as anti-Fourier heat flux, where heat flows from cold regions to hot (Sone Reference Sone2007), and flow near boundaries governed by the dynamics inside Knudsen layers (Loyalka Reference Loyalka1975). Although the Boltzmann equation usually provides an accurate description across all values of
$\mathit{Kn}^{\prime }$
, in many microflows, the Mach number is small and
$0.01\lesssim \mathit{Kn}^{\prime }\lesssim 1$
(based on
$0.1~\unicode[STIX]{x03BC}\text{m}\lesssim L\lesssim 10~\unicode[STIX]{x03BC}\text{m}$
), so that the cost of three-dimensional (3D) computations using conventional methods such as direct simulation Monte Carlo (DSMC) can be huge.
To overcome the aforementioned challenges, there has been a resurgence of interest in using moment methods on the Boltzmann equation to derive systems of partial differential equations, a method originally pioneered by Grad (Reference Grad1949). The first five moments are the conserved quantities (the mass density
$\unicode[STIX]{x1D70C}$
, momentum density
$\unicode[STIX]{x1D70C}v_{i}$
and internal energy density
$\unicode[STIX]{x1D70C}\unicode[STIX]{x1D700}$
), and using Grad’s approach of closure these would lead to the Euler equations, which, in order to develop a hierarchy, we will label G5. The next higher-order moments that are most natural to bring into the system are the heat flux
$q_{i}$
and deviatoric stress tensor
$\unicode[STIX]{x1D61A}_{ij}$
, and these give an additional
$3+5=8$
moments, leading to Grad’s 13-moment system (G13).
Although G13 are stable and extend the NSF equations, they cannot describe continuous shock structures above a critical Mach number and do not capture Knudsen boundary layers, arguably the most important feature of microflows (Au, Torrilhon & Weiss Reference Au, Torrilhon and Weiss2001; Torrilhon & Struchtrup Reference Torrilhon and Struchtrup2004). In order to overcome these drawbacks, Struchtrup and Torrilhon proposed a regularisation of Grad’s approach based on an ‘order of magnitude method’, see Struchtrup (Reference Struchtrup2005), which identifies which terms to retain in the closure relations at every level of the hierarchy to obtain a consistent level of accuracy in terms of
$\mathit{Kn}^{\prime }$
. Reassuringly, in this approach, the regularisation of Euler equations (G5) results in the Navier–Stokes system (R5). At the next level, one obtains the G13/R13 system, described in detail in Struchtrup (Reference Struchtrup2005), and usually derived for Maxwell molecules. The R13 system was recently the subject of an Annual Review of Fluid Mechanics article (Torrilhon Reference Torrilhon2016), and, promisingly, it is third-order accurate in
$\mathit{Kn}^{\prime }$
(G13 is second order), permits smooth shock structures and predicts the existence of Knudsen layers.
For many microscale gas flows, it is sufficient to consider the linearised form of the R13, which is valid for the low-Reynolds-number flows usually encountered at the microscale. Notably, even in this simplified setting, the solution of the R13 system still poses a significant challenge and, consequently, thus far it has only been applied to canonical one- and two-dimensional problems using both analytic approaches (Struchtrup Reference Struchtrup2005; Torrilhon Reference Torrilhon2016) and numerical methods based on standard discretisation techniques (Gu & Emerson Reference Gu and Emerson2009; Rana, Torrilhon & Struchtrup Reference Rana, Torrilhon and Struchtrup2013). The computation of such flows will be expensive in 3D, particularly for flow around objects where the velocity field decay is slow so that the computational mesh must extend far from the object in order to achieve domain-independent results.
In classical Stokes flow problems, there is a huge body of research into ‘singularity methods’ based on fundamental solutions that represent the response of a flow to a singular point force. The primary singularity is the Stokeslet, and from its derivatives a host of other singularities can be derived (rotlets, stresslets, etc.). These solutions are routinely exploited in a number of ways; for example, they can be used to construct flow profiles over various body shapes (Chwang & Wu Reference Chwang and Wu1975) or as the basis of the powerful reduced-dimensionality boundary integral method (Pozrikidis Reference Pozrikidis1992). These methods have been applied to numerous liquid and gas microflows, such as in the locomotion of micro-organisms (Lauga & Powers Reference Lauga and Powers2009), but have only recently been mentioned in the context of gas microflows.
The first steps towards harnessing the power of the aforementioned methods for rarefied gas flows were taken by Lockerby & Collyer (Reference Lockerby and Collyer2016), who derived fundamental solutions for the G13 system and utilised them in the method of fundamental solutions (MFS) to solve a number of canonical problems. This paper also suggested a starting point for a derivation of the R13 system, but a full solution was not presented. The G13 ‘Gradlets’ can actually be derived as a natural extension of the Stokeslets, with the same number of boundary conditions required at a solid surface (three on velocity/stress and one on temperature/heat flux). In contrast, the R13 system represents a step change in complexity due to the appearance of higher-order derivatives in the equations alongside the requirement of satisfying an additional five boundary conditions at a solid surface (nine in total). These are the challenges that have been overcome in this article, culminating in a new efficient simulation tool for 3D rarefied gas microflows.
2 Problem formulation
The steady linearised equations consider small deviations from an equilibrium state of density
$\hat{\unicode[STIX]{x1D70C}}_{e}$
, temperature
$\hat{T}_{e}$
, vanishing velocity
$\hat{\boldsymbol{v}}$
, deviatoric stress
$\hat{\unicode[STIX]{x1D64E}}$
and heat flux
$\hat{\boldsymbol{q}}$
, with dimensional quantities denoted by a hat. In this setting, introducing
$\hat{\unicode[STIX]{x1D703}}=\hat{R}\hat{T}$
with
$\hat{R}$
the specific gas constant, the linearised ideal gas law (valid for
$\hat{\unicode[STIX]{x1D70C}}\ll \hat{\unicode[STIX]{x1D70C}}_{e}$
and
$\hat{\unicode[STIX]{x1D703}}\ll \hat{\unicode[STIX]{x1D703}}_{e}$
) for pressure is
$\hat{p}=\hat{\unicode[STIX]{x1D70C}}_{e}\hat{\unicode[STIX]{x1D703}}+\hat{\unicode[STIX]{x1D70C}}\hat{\unicode[STIX]{x1D703}}_{e}$
.
Taking characteristic scales for length
$\hat{L}$
, velocity
$\sqrt{\hat{\unicode[STIX]{x1D703}}_{e}}$
, stress
$\hat{\unicode[STIX]{x1D70C}}_{e}\hat{\unicode[STIX]{x1D703}}_{e}$
and heat flux
$\hat{\unicode[STIX]{x1D70C}}_{e}\hat{\unicode[STIX]{x1D703}}_{e}^{3/2}$
, the conservation laws of mass, momentum and energy are
$$\begin{eqnarray}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{v}=0,\quad \unicode[STIX]{x1D735}p+\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D64E}=0\quad \text{and}\quad \unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{q}=0.\end{eqnarray}$$
The differences between the frameworks lie in the formulation of the constitutive relations for the heat flux and deviatoric stress. In order to highlight the additional terms that G13 and R13 add to the usual NSF closure, these can be written conveniently as (Torrilhon Reference Torrilhon2016)
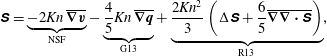$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D64E}=\underbrace{-2\mathit{Kn}\,\overline{\unicode[STIX]{x1D735}\boldsymbol{v}}}_{\text{NSF}}-\underbrace{\frac{4}{5}\mathit{Kn}\,\overline{\unicode[STIX]{x1D735}\boldsymbol{q}}}_{\text{G13}}+\underbrace{\frac{2\mathit{Kn}^{2}}{3}\left(\unicode[STIX]{x0394}\unicode[STIX]{x1D64E}+\frac{6}{5}\overline{\unicode[STIX]{x1D735}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D64E}}\right)}_{\text{R13}}, & \displaystyle\end{eqnarray}$$
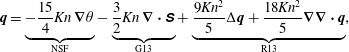$$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{q}=\underbrace{-\frac{15}{4}\mathit{Kn}\,\unicode[STIX]{x1D735}\unicode[STIX]{x1D703}}_{\text{NSF}}-\underbrace{\frac{3}{2}\mathit{Kn}\,\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D64E}}_{\text{G13}}+\underbrace{\frac{9\mathit{Kn}^{2}}{5}\unicode[STIX]{x0394}\boldsymbol{q}+\frac{18\mathit{Kn}^{2}}{5}\unicode[STIX]{x1D735}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{q}}_{\text{R13}}, & \displaystyle\end{eqnarray}$$
$\overline{(\cdot )}$
, means that the trace-free symmetric component of a tensor should be taken (for example
$(\overline{\unicode[STIX]{x1D735}\boldsymbol{q}})_{ij}=(1/2)(\unicode[STIX]{x1D6FB}_{j}q_{i}+\unicode[STIX]{x1D6FB}_{i}q_{j})-(1/3)\unicode[STIX]{x1D6FF}_{ij}^{K}\unicode[STIX]{x1D6FB}_{k}q_{k}$
, where
$\unicode[STIX]{x1D6FF}_{ij}^{K}$
is the Kronecker delta), and a scaled Knudsen number has been introduced as 
$$\begin{eqnarray}\mathit{Kn}=\frac{\hat{\unicode[STIX]{x1D707}}_{e}}{\hat{\unicode[STIX]{x1D70C}}_{e}\hat{L}\hat{\unicode[STIX]{x1D703}}_{e}^{1/2}}=\sqrt{\frac{2}{\unicode[STIX]{x03C0}}}\frac{\hat{\unicode[STIX]{x1D706}}_{e}}{\hat{L}},\end{eqnarray}$$
where
$\hat{\unicode[STIX]{x1D706}}_{e}$
and
$\hat{\unicode[STIX]{x1D707}}_{e}$
are the mean free path and dynamic viscosity of the equilibrium state respectively.
Notably, we have eliminated the higher-order moments
$R$
(scalar),
$\unicode[STIX]{x1D64D}$
(rank-2 tensor) and
$\unicode[STIX]{x1D662}$
(rank-3 tensor) of the R13 system, which appear on the right-hand side of (2.2a
) as
$-\mathit{Kn}\,\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D662}$
and the right-hand side of (2.2b
) as
$-(1/4)\mathit{Kn}(3\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D64D}+\unicode[STIX]{x1D735}R)$
, using the R13 closure relations,
$$\begin{eqnarray}R=-12\mathit{Kn}\,\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{q},\quad \unicode[STIX]{x1D64D}=-{\textstyle \frac{24}{5}}\mathit{Kn}\,\overline{\unicode[STIX]{x1D735}\boldsymbol{q}}\quad \text{and}\quad \unicode[STIX]{x1D662}=-2\mathit{Kn}\,\overline{\unicode[STIX]{x1D735}\unicode[STIX]{x1D64E}}.\end{eqnarray}$$
These terms, which were excluded by Grad, introduce higher derivatives than found in the G13 system and hence require the formulation of additional boundary conditions.
2.1 The R13 boundary conditions
Consider an impermeable solid surface with outward unit normal
$\boldsymbol{n}$
and tangent vectors
$\boldsymbol{t}_{1},\boldsymbol{t}_{2}$
, so that subscripts
$n,t_{1},t_{2}$
correspond to the projection of a particular moment onto these directions. Only the fluxes with odd normal components need to be prescribed at the wall (Torrilhon Reference Torrilhon2016), so that the NSF/G13 system requires four conditions on the variables
$v_{n}$
,
$S_{nt_{i}}$
,
$q_{n}$
. These are derived from Maxwell’s accommodation model with diffuse reflection. For a surface with wall velocity
$\boldsymbol{v}^{w}$
and temperature
$\unicode[STIX]{x1D703}^{w}$
, the wall conditions are given by
$$\begin{eqnarray}v_{n}^{w}=\underbrace{v_{n}}_{\text{NSF}},\end{eqnarray}$$
$$\begin{eqnarray}v_{t_{i}}^{w}=\underbrace{v_{t_{i}}}_{\text{NSF}}+\underbrace{\unicode[STIX]{x1D6FD}^{-1}S_{nt_{i}}+{\textstyle \frac{1}{5}}q_{t_{i}}}_{\text{G13}}+\underbrace{{\textstyle \frac{1}{2}}m_{nnt_{i}}}_{\text{R13}}\quad (i=1,2),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D703}^{w}=\underbrace{\unicode[STIX]{x1D703}}_{\text{NSF}}+\underbrace{{\textstyle \frac{1}{2}}\unicode[STIX]{x1D6FD}^{-1}\,q_{n}+{\textstyle \frac{1}{4}}S_{nn}}_{\text{G13}}+\underbrace{{\textstyle \frac{5}{56}}R_{nn}+{\textstyle \frac{1}{30}}R}_{\text{R13}},\end{eqnarray}$$
where
$\unicode[STIX]{x1D6FD}=\sqrt{2/\unicode[STIX]{x03C0}}$
. Higher-order contributions (from G13) are often retained in the NSF formulation to create velocity slip and temperature-jump conditions.
For R13, Maxwell’s model gives an additional five boundary conditions associated with the odd normal components
$R_{nt_{1}}$
,
$R_{nt_{2}}$
,
$m_{nt_{1}t_{2}}$
,
$m_{nnn}$
and
$m_{nt_{1}t_{1}}$
(as
$\unicode[STIX]{x1D662}$
is trace-free, a condition on the odd normal moment
$m_{nt_{2}t_{2}}$
is redundant), given by
$$\begin{eqnarray}v_{t_{i}}^{w}=v_{t_{i}}-\unicode[STIX]{x1D6FD}^{-1}\,R_{nt_{i}}-{\textstyle \frac{1}{2}}m_{nnt_{i}}-{\textstyle \frac{11}{5}}q_{t_{i}}\quad (i=1,2),\end{eqnarray}$$
$$\begin{eqnarray}0=\unicode[STIX]{x1D6FD}^{-1}\,m_{nt_{1}t_{2}}+{\textstyle \frac{1}{14}}R_{t_{1}t_{2}}+S_{t_{1}t_{2}},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D703}^{w}=\unicode[STIX]{x1D703}-{\textstyle \frac{5}{2}}\left({\textstyle \frac{7}{5}}S_{nn}+{\textstyle \frac{1}{14}}R_{nn}+\unicode[STIX]{x1D6FD}^{-1}\,m_{nnn}-{\textstyle \frac{1}{75}}R\right),\end{eqnarray}$$
$$\begin{eqnarray}0=\unicode[STIX]{x1D6FD}^{-1}\left(m_{nt_{1}t_{1}}+\frac{m_{nnn}}{2}\right)+\frac{1}{14}\left(R_{t_{1}t_{1}}+\frac{R_{nn}}{2}\right)+\left(S_{t_{1}t_{1}}+\frac{S_{nn}}{2}\right).\end{eqnarray}$$
Notably, the boundary conditions have all been written in a form where the inputs (
$\boldsymbol{v}^{w}$
and
$\unicode[STIX]{x1D703}^{w}$
) are isolated on the left-hand side, which is convenient for the MFS implementation.
2.2 Summary
The R13 system requires the solution of 13 bulk equations, the usual five from conservation laws (2.1) alongside eight constitutive evolution equations (2.2), with nine boundary conditions applied at impermeable solid walls (2.5). Our approach to solving these equations requires us to now derive the fundamental solutions of this system.
3 R13 fundamental solutions
For the linearised NSF system, the fundamental solutions for the momentum and energy equation are well known, namely the Stokeslet and the Green’s function for the Laplacian. Furthermore, higher-order singularities based on the Stokeslet’s derivatives (doublet, quadrupole, etc.) or point sources of mass (source, source doublet, etc.) have also been derived. In Lockerby & Collyer (Reference Lockerby and Collyer2016), this analysis was extended to derive the first fundamental solutions to the G13 system; however, attempts to derive R13 fundamental solutions were not completed due to the increased complexity of the R13 system.
Fundamental solutions to the NSF/G13 systems are obtained by calculating the response of the conservation equations of momentum and energy (2.1) to point sources of force
$\boldsymbol{f}\,\unicode[STIX]{x1D6FF}(\boldsymbol{r})$
and heat
$g\unicode[STIX]{x1D6FF}(\boldsymbol{r})$
respectively, resulting in four degrees of freedom (three from
$\boldsymbol{f}$
and one from
$g$
) that can be used in the MFS to satisfy the required four boundary conditions. For the R13 system, not only will these basic fundamental solutions differ from the NSF/G13 systems, but an additional fundamental solution will be obtained from finding the response of the constitutive relation for the deviatoric stress (2.2a
) to a point source
$\unicode[STIX]{x1D642}\unicode[STIX]{x1D6FF}(\boldsymbol{r})$
, yielding the required five more degrees of freedom from the trace-free symmetric rank-2 tensor
$\unicode[STIX]{x1D642}$
. A deeper understanding of how to structure point sources in higher-order moment equations remains an open problem, but building on the NSF/G13 system in this manner will be shown to be a sensible starting point.
The full driven system to be investigated is therefore
$$\begin{eqnarray}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{v}=0,\quad \unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{q}=g\unicode[STIX]{x1D6FF}(\boldsymbol{r}),\quad \unicode[STIX]{x1D735}p+\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D64E}=\boldsymbol{f}\,\unicode[STIX]{x1D6FF}(\boldsymbol{r}),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D64E}=-2\mathit{Kn}\,\overline{\unicode[STIX]{x1D735}\boldsymbol{v}}-\frac{4}{5}\mathit{Kn}\,\overline{\unicode[STIX]{x1D735}\boldsymbol{q}}+\frac{2\mathit{Kn}^{2}}{3}\left(\unicode[STIX]{x0394}\unicode[STIX]{x1D64E}+\frac{6}{5}\overline{\unicode[STIX]{x1D735}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D64E}}\right)+\unicode[STIX]{x1D642}\unicode[STIX]{x1D6FF}(\boldsymbol{r}),\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{q}=-\frac{15}{4}\mathit{Kn}\,\unicode[STIX]{x1D735}\unicode[STIX]{x1D703}-\frac{3}{2}\mathit{Kn}\,\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D64E}+\frac{9\mathit{Kn}^{2}}{5}\unicode[STIX]{x0394}\boldsymbol{q}+\frac{18\mathit{Kn}^{2}}{5}\unicode[STIX]{x1D735}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{q}.\end{eqnarray}$$
3.1 Deriving fundamental solutions
The fundamental solutions were derived using two independent methods, each yielding the same result, one utilising Fourier transforms and the other directly manipulating the equations by exploiting the properties of known fundamental solutions (see Lisicki (Reference Lisicki2013) for a range of methods). It was assumed that all quantities vanish as
$r\rightarrow \infty$
, where
$r=\Vert \boldsymbol{r}\Vert$
is the distance from the origin.
Interestingly, the R13 fundamental solutions can be decomposed into contributions from classical solutions and their derivatives. For the G13/NSF system, one requires the fundamental solution to Laplace’s equation,
$$\begin{eqnarray}\unicode[STIX]{x0394}\unicode[STIX]{x1D719}=-\unicode[STIX]{x1D6FF}(\boldsymbol{r})\quad \text{with solution}~\unicode[STIX]{x1D719}=\frac{1}{4\unicode[STIX]{x03C0}r},\end{eqnarray}$$
and the biharmonic equation,
$$\begin{eqnarray}\unicode[STIX]{x0394}\unicode[STIX]{x0394}\unicode[STIX]{x1D713}=-\unicode[STIX]{x1D6FF}(\boldsymbol{r})\quad \text{with solution}~\unicode[STIX]{x1D713}=\frac{r}{8\unicode[STIX]{x03C0}}.\end{eqnarray}$$
Notably, the R13 system also requires solutions to the Helmholtz equation,
$$\begin{eqnarray}(\unicode[STIX]{x0394}-\unicode[STIX]{x1D6FE}^{2})\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FE}}=\unicode[STIX]{x1D6FF}(\boldsymbol{r})\quad \text{with solution}~\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FE}}=-\frac{\text{e}^{-\unicode[STIX]{x1D6FE}r}}{4\unicode[STIX]{x03C0}r}=-\text{e}^{-\unicode[STIX]{x1D6FE}r}\unicode[STIX]{x1D719},\end{eqnarray}$$
which brings into the system exponential terms that will form the Knudsen layer, with
$\unicode[STIX]{x1D6FE}$
the parameter characterising the decay rate.
The full set of fundamental solutions will be given in § 3.2, but before doing so, we outline the method based on Fourier transforms in order to calculate the response of the system to a point source of heat only (i.e.
$\boldsymbol{f}=\unicode[STIX]{x1D642}=\mathbf{0}$
in (3.1)). Due to linearity, the responses to each source can be calculated separately and then superimposed.
3.1.1 Derivation of response to a point heat source
The starting point is to take the divergence of (3.1d ) twice, to give
$$\begin{eqnarray}\unicode[STIX]{x1D6FB}_{i}\unicode[STIX]{x1D6FB}_{j}\unicode[STIX]{x1D61A}_{ij}=-\frac{8\mathit{Kn}\,g}{15}\unicode[STIX]{x0394}\unicode[STIX]{x1D6FF}(\boldsymbol{r})+\frac{6\mathit{Kn}^{2}}{5}\unicode[STIX]{x0394}\unicode[STIX]{x1D6FB}_{i}\unicode[STIX]{x1D6FB}_{j}\unicode[STIX]{x1D61A}_{ij},\end{eqnarray}$$
where
$\unicode[STIX]{x0394}=\unicode[STIX]{x1D6FB}_{k}\unicode[STIX]{x1D6FB}_{k}$
is the Laplace operator, which can be rearranged into the form of a Helmholtz equation,
$$\begin{eqnarray}(\unicode[STIX]{x0394}-\unicode[STIX]{x1D6FE}_{2}^{2})\unicode[STIX]{x1D6FB}_{i}\unicode[STIX]{x1D6FB}_{j}\unicode[STIX]{x1D61A}_{ij}=-\frac{8\unicode[STIX]{x1D6FE}_{2}^{2}\mathit{Kn}\,g}{15}\unicode[STIX]{x0394}\unicode[STIX]{x1D6FF}(\boldsymbol{r}),\end{eqnarray}$$
with
$\unicode[STIX]{x1D6FE}_{2}^{2}=5/6\mathit{Kn}^{2}$
.
Defining the Fourier transform and corresponding inverse as
$$\begin{eqnarray}{\mathcal{F}}[f(\boldsymbol{r})]=\tilde{f}(\boldsymbol{k})=\int _{\mathbb{R}^{3}}\,f(\boldsymbol{r})\text{e}^{-\text{i}\,\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{r}}\,\text{d}\boldsymbol{r}\quad \text{and}\quad {\mathcal{F}}^{-1}[\tilde{f}(\boldsymbol{k})]=f(\boldsymbol{r})=\frac{1}{(2\unicode[STIX]{x03C0})^{3}}\int _{\mathbb{R}^{3}}\,\tilde{f}(\boldsymbol{k})\text{e}^{\text{i}\,\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{r}}\,\text{d}\boldsymbol{k},\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{F}}[\unicode[STIX]{x1D735}f(\boldsymbol{r})]=\text{i}\,\boldsymbol{k}\tilde{f}(\boldsymbol{k}),\quad {\mathcal{F}}[\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{f}(\boldsymbol{r})]=\text{i}\,\boldsymbol{k}\boldsymbol{\cdot }\tilde{\boldsymbol{f}}(\boldsymbol{k})\quad \text{and}\quad {\mathcal{F}}[\unicode[STIX]{x0394}f(\boldsymbol{r})]=-k^{2}\tilde{f}(\boldsymbol{k}),\end{eqnarray}$$
the transform of (3.6) becomes
$$\begin{eqnarray}-\tilde{\unicode[STIX]{x1D61A}}_{ij}k_{i}k_{j}=\frac{8\unicode[STIX]{x1D6FE}_{2}^{2}\mathit{Kn}\,g}{15}\frac{k^{2}}{\unicode[STIX]{x1D6FE}_{2}^{2}+k^{2}},\end{eqnarray}$$
where
$k=\Vert \boldsymbol{k}\Vert$
. Noting that the Fourier transform of the Helmholtz fundamental solution (3.4) gives
$$\begin{eqnarray}{\mathcal{F}}[\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FE}_{2}}]=-\frac{1}{k^{2}+\unicode[STIX]{x1D6FE}_{2}^{2}},\end{eqnarray}$$
and that
${\mathcal{F}}[\unicode[STIX]{x0394}f(\boldsymbol{x})]=-k^{2}\tilde{f}(\boldsymbol{k})$
, the inverse transform of (3.9) is found to be
$$\begin{eqnarray}\unicode[STIX]{x1D6FB}_{i}\unicode[STIX]{x1D6FB}_{j}\unicode[STIX]{x1D61A}_{ij}=\frac{8\unicode[STIX]{x1D6FE}_{2}^{2}\mathit{Kn}\,g}{15}\unicode[STIX]{x0394}\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FE}_{2}}.\end{eqnarray}$$
Taking the divergence of the momentum equation in (3.1a–c ) and using (3.11) then immediately gives the required solution for pressure,
$$\begin{eqnarray}p=-\frac{8\unicode[STIX]{x1D6FE}_{2}^{2}\mathit{Kn}\,g}{15}\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FE}_{2}}.\end{eqnarray}$$
The other variables are found using the same method; that is, by taking the Fourier transform of the required equations to reduce them to an algebraic equation for the corresponding variable and making appropriate substitutions using the known Fourier transforms of (3.4).
3.2 The fundamental solutions
The fundamental solutions are
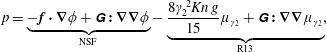$$\begin{eqnarray}\displaystyle & \displaystyle p=\underbrace{-\boldsymbol{f}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D719}+\unicode[STIX]{x1D642}\boldsymbol{ : }\unicode[STIX]{x1D735}\unicode[STIX]{x1D735}\unicode[STIX]{x1D719}}_{\text{NSF}}-\underbrace{\frac{8\unicode[STIX]{x1D6FE}_{2}^{2}\mathit{Kn}\,g}{15}\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FE}_{2}}+\unicode[STIX]{x1D642}\boldsymbol{ : }\unicode[STIX]{x1D735}\unicode[STIX]{x1D735}\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FE}_{2}}}_{\text{R13}}, & \displaystyle\end{eqnarray}$$
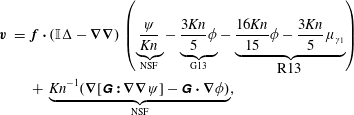$$\begin{eqnarray}\displaystyle \displaystyle \boldsymbol{v} & = & \displaystyle \boldsymbol{f}\boldsymbol{\cdot }(\mathbb{I}\unicode[STIX]{x0394}-\unicode[STIX]{x1D735}\unicode[STIX]{x1D735})\left(\underbrace{\frac{\unicode[STIX]{x1D713}}{Kn}}_{\text{NSF}}-\underbrace{\frac{3\mathit{Kn}}{5}\unicode[STIX]{x1D719}}_{\text{G13}}-\underbrace{\frac{16\mathit{Kn}}{15}\unicode[STIX]{x1D719}-\frac{3\mathit{Kn}}{5}\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FE}_{1}}}_{R13}\right)\nonumber\\ \displaystyle & & \displaystyle +\,\underbrace{\mathit{Kn}^{-1}(\unicode[STIX]{x1D735}[\unicode[STIX]{x1D642}\boldsymbol{ : }\unicode[STIX]{x1D735}\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}]-\unicode[STIX]{x1D642}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D719})}_{\text{NSF}},\end{eqnarray}$$
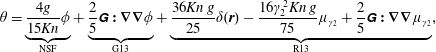$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D703}=\underbrace{\frac{4g}{15Kn}\unicode[STIX]{x1D719}}_{\text{NSF}}+\underbrace{\frac{2}{5}\unicode[STIX]{x1D642}\boldsymbol{ : }\unicode[STIX]{x1D735}\unicode[STIX]{x1D735}\unicode[STIX]{x1D719}}_{\text{G13}}+\underbrace{\frac{36\mathit{Kn}\,g}{25}\unicode[STIX]{x1D6FF}(\boldsymbol{r})-\frac{16\unicode[STIX]{x1D6FE}_{2}^{2}\mathit{Kn}\,g}{75}\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FE}_{2}}+\frac{2}{5}\unicode[STIX]{x1D642}\boldsymbol{ : }\unicode[STIX]{x1D735}\unicode[STIX]{x1D735}\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FE}_{2}}}_{\text{R13}},\qquad & \displaystyle\end{eqnarray}$$
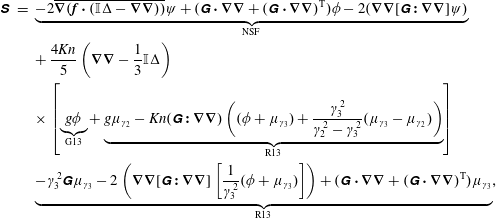$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D64E} & = & \displaystyle \underbrace{-2\overline{\unicode[STIX]{x1D735}(\boldsymbol{f}\boldsymbol{\cdot }(\mathbb{I}\unicode[STIX]{x0394}-\unicode[STIX]{x1D735}\unicode[STIX]{x1D735}))}\unicode[STIX]{x1D713}+(\unicode[STIX]{x1D642}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D735}+(\unicode[STIX]{x1D642}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D735})^{\text{T}})\unicode[STIX]{x1D719}-2(\unicode[STIX]{x1D735}\unicode[STIX]{x1D735}[\unicode[STIX]{x1D642}\boldsymbol{ : }\unicode[STIX]{x1D735}\unicode[STIX]{x1D735}]\unicode[STIX]{x1D713})}_{\text{NSF}}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{4\mathit{Kn}}{5}\left(\unicode[STIX]{x1D735}\unicode[STIX]{x1D735}-\frac{1}{3}\mathbb{I}\unicode[STIX]{x0394}\right)\nonumber\\ \displaystyle & & \displaystyle \times \left[\underbrace{g\unicode[STIX]{x1D719}}_{\text{G13}}+\underbrace{g\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FE}_{2}}-Kn(\unicode[STIX]{x1D642}\boldsymbol{ : }\unicode[STIX]{x1D735}\unicode[STIX]{x1D735})\left((\unicode[STIX]{x1D719}+\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FE}_{3}})+\frac{\unicode[STIX]{x1D6FE}_{3}^{2}}{\unicode[STIX]{x1D6FE}_{2}^{2}-\unicode[STIX]{x1D6FE}_{3}^{2}}(\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FE}_{3}}-\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FE}_{2}})\right)}_{\text{R13}}\right]\nonumber\\ \displaystyle & & \displaystyle \underbrace{-\unicode[STIX]{x1D6FE}_{3}^{2}\unicode[STIX]{x1D642}\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FE}_{3}}-2\left(\unicode[STIX]{x1D735}\unicode[STIX]{x1D735}[\unicode[STIX]{x1D642}\boldsymbol{ : }\unicode[STIX]{x1D735}\unicode[STIX]{x1D735}]\left[\frac{1}{\unicode[STIX]{x1D6FE}_{3}^{2}}(\unicode[STIX]{x1D719}+\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FE}_{3}})\right]\right)+(\unicode[STIX]{x1D642}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D735}+(\unicode[STIX]{x1D642}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D735})^{\text{T}})\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FE}_{3}}}_{\text{R13}},\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{q}=\underbrace{-g\unicode[STIX]{x1D735}\unicode[STIX]{x1D719}}_{\text{NSF}}+\frac{3\mathit{Kn}}{2}\boldsymbol{f}\boldsymbol{\cdot }(\mathbb{I}\unicode[STIX]{x0394}-\unicode[STIX]{x1D735}\unicode[STIX]{x1D735})(\underbrace{\unicode[STIX]{x1D719}}_{\text{G13}}+\underbrace{\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FE}_{1}}}_{\text{R13}}),\end{eqnarray}$$
$\unicode[STIX]{x1D6FE}_{1}^{2}=(5/9)\mathit{Kn}^{-2}$
,
$\unicode[STIX]{x1D6FE}_{2}^{2}=(5/6)\mathit{Kn}^{-2}$
and
$\unicode[STIX]{x1D6FE}_{3}^{2}=(3/2)\mathit{Kn}^{-2}$
. These are the exponential functions that superpose to form the Knudsen layer in the R13 system. It is therefore critical that all decay rates are obtained, and, notably,
$\unicode[STIX]{x1D6FE}_{3}$
can only be obtained as a response to the point source in (3.1d
). At the NSF level, this source creates Stokes doublet terms in (3.13a
) and (3.13b
), i.e. directional derivatives of the Stokeslet; however, these are not required in an NSF-MFS scheme (or G13), so
$\unicode[STIX]{x1D642}=\mathbf{0}$
can be used in this case.
The solutions both extend the R13 solutions derived in Lockerby & Collyer (Reference Lockerby and Collyer2016) in number and also generalise the approach by making no assumptions on the flow class in order to obtain the complete solution set. For example, the R13 solutions in Lockerby & Collyer (Reference Lockerby and Collyer2016) for isobaric stationary flow miss out the thermally driven pressure and stress fields. Notably, however, all computed solutions in their article were for the G13 system, and these agree with our results.
The fundamental solutions derived above have been obtained using two independent methods and have been verified using Wolfram Mathematica.
4 Method of fundamental solutions
The MFS (Fairweather & Karageorghis Reference Fairweather and Karageorghis1998; Young et al.
Reference Young, Jane, Fan, Murugesan and Tsai2006) will be used as a simple-to-implement numerical scheme to demonstrate how the fundamental solutions obtained in § 3 allow us to simulate 3D micro-gas-flows. Future work will develop these ideas towards a boundary integral method; however, the MFS is simpler to implement as fundamental solutions are placed outside the flow domain (at singularity sites), so that inside the fluid their contributions are non-singular and satisfy the equations of motion (by design). The solution is then represented as a superposition of fundamental solutions, and the weights of each solution (the
$\boldsymbol{f}$
,
$g$
and
$\unicode[STIX]{x1D642}$
) are obtained by insisting that the relevant boundary conditions are satisfied (at boundary nodes).
As our focus is on the development of the fundamental solutions, the simplest variant of the MFS is implemented, in which the
$N$
singularity sites are (a) distributed over a surface and (b) equal in number to the boundary nodes (creating a square matrix). Notably, the MFS is particularly convenient for external flows (Lockerby & Collyer Reference Lockerby and Collyer2016), as the fundamental solutions automatically satisfy far-field boundary conditions, so that the fluid domain does not have to be artificially truncated, as in many classical numerical methods.
4.1 Implementation
The
$N$
singularity sites and boundary nodes are at
$\{\boldsymbol{x}_{i}^{s}\}_{i=1}^{N}$
and
$\{\boldsymbol{x}_{j}^{b}\}_{j=1}^{N}$
respectively; the choice of their placement will be discussed in § 5.1. The displacements
$\boldsymbol{r}_{i}$
and
$\boldsymbol{r}_{ij}$
from the
$i$
th singularity site to a position
$\boldsymbol{x}$
and
$j$
th boundary node
$\boldsymbol{x}_{j}^{b}$
respectively are then
$$\begin{eqnarray}\boldsymbol{r}_{i}=\boldsymbol{x}-\boldsymbol{x}_{i}^{s},\quad \boldsymbol{r}_{ij}=\boldsymbol{x}_{j}^{b}-\boldsymbol{x}_{i}^{s}.\end{eqnarray}$$
The 13 flow variables will be represented in an array
$\boldsymbol{Y}=\{p,v_{1},v_{2},v_{3},\unicode[STIX]{x1D703},S_{11},S_{12},S_{13},S_{22},S_{23},q_{1},q_{2},q_{3}\}^{\text{T}}$
of dimension
$13\times 1$
, while the weights associated with the fundamental solution at each singularity site are given as an array
$\{\boldsymbol{X}_{i}\}_{i=1}^{N}=\{g_{i},f_{i}^{1},f_{i}^{2},f_{i}^{3},G_{i}^{11},G_{i}^{12},G_{i}^{13},G_{i}^{22},G_{i}^{23}\}^{\text{T}}$
of size
$9\times 1$
. The flow variables are then represented as a superposition of contributions from all singularity sites as
$$\begin{eqnarray}\boldsymbol{Y}(\boldsymbol{x})=\mathop{\sum }_{i=1}^{N}\unicode[STIX]{x1D63C}(\boldsymbol{r}_{i})\boldsymbol{\cdot }\boldsymbol{X}_{i},\end{eqnarray}$$
where
$\unicode[STIX]{x1D63C}$
is a coefficient matrix of size
$13\times 9$
. The entry
$\unicode[STIX]{x1D608}_{mn}$
is obtained from the equations for the flow variables (3.13a
)–(3.13e
) by extracting the coefficient of the
$n$
th weight from the
$m$
th equation. For example,
$A_{16}$
would be the coefficient of weight
$G^{12}$
in (3.13a
), i.e.
$\unicode[STIX]{x1D735}_{1}\unicode[STIX]{x1D735}_{2}(\unicode[STIX]{x1D719}+\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FE}_{2}})$
. It should be noted that, up to this point, we have not specified a coordinate system, but in our implementation we use Cartesian coordinates, so that
$\unicode[STIX]{x1D735}_{1}\unicode[STIX]{x1D735}_{2}=\unicode[STIX]{x2202}_{x}\unicode[STIX]{x2202}_{y}$
.
The flow variables at each boundary node are obtained from (4.2),
$$\begin{eqnarray}\boldsymbol{Y}(\boldsymbol{x}_{j}^{b})=\mathop{\sum }_{i=1}^{N}\unicode[STIX]{x1D63C}(\boldsymbol{r}_{ij})\boldsymbol{\cdot }\boldsymbol{X}_{i},\end{eqnarray}$$
which is inserted into the right-hand side of (2.5) to construct a linear system of equations of size
$9N\times 9N$
, i.e.
$$\begin{eqnarray}{\mathcal{B}}={\mathcal{C}}\cdot {\mathcal{X}},\end{eqnarray}$$
where
${\mathcal{B}}$
contains the
$9N$
boundary values (i.e. the left-hand side of (2.5)),
${\mathcal{X}}$
contains the
$9N$
singularity weights, and the
$9N\times 9N$
matrix
${\mathcal{C}}$
connects the contribution of each singularity weight to each boundary value. The singularity weights are the unknowns, which can be found using standard inversion methods.
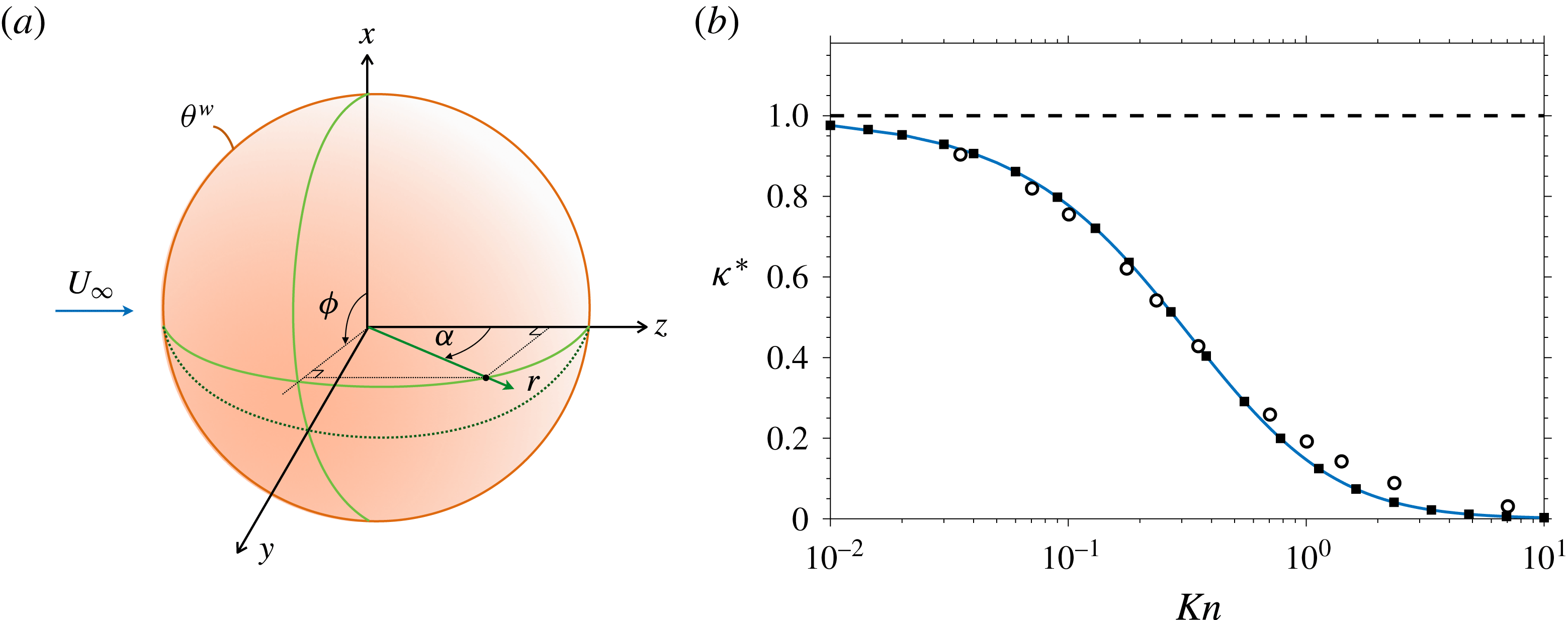
Figure 1. (a) Schematic of the general problem considered in §§ 5.2–5.3. A sphere uniformly heated to
$\unicode[STIX]{x1D703}^{w}$
is placed in a steady rarefied gas flow of speed
$U_{\infty }$
. Normal spherical coordinates
$(r,\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D719})$
are employed to describe the problem, but all calculations are carried out in Cartesian coordinates. (b) Effective heat conductivity,
$\unicode[STIX]{x1D705}^{\ast }$
, versus Knudsen number for heat transfer from a stationary sphere (
$\unicode[STIX]{x1D703}^{w}=1$
,
$U_{\infty }=0$
): the results from NSF (– – –), R13 analytic (——), and R13-MFS (▪) theories are compared with solutions to the linearised Boltzmann equation (○) (Chernyak & Margilevskiy Reference Chernyak and Margilevskiy1989).
5 R13-MFS results
Given that analytic solutions to the NSF system are rare, it is of little surprise that there are few R13 analytic results that can be used as benchmarks for our new method. However, for two canonical problems, heat transfer from a sphere and creeping flow around a sphere (figure 1 a), analytic solutions are available to establish the accuracy of the R13-MFS scheme. In the former case, in § 5.2, a new analytic solution is derived for R13, which exhibits a Knudsen layer not present for NSF/G13. In the latter case, in § 5.3, an analytic solution has been obtained by Torrilhon (Reference Torrilhon2010), although its complexity is such that, as a by-product, our computations will verify its accuracy also. Having established the accuracy of the new approach, the flow and force generated by the hydrodynamic interaction between two approaching spheres is calculated in § 5.4.
5.1 MFS parameters
To simulate a single sphere, with relevant length scale
$\hat{L}$
equal to the radius of the sphere, both boundary nodes and singularity sites were evenly distributed over spheres of dimensionless radius 1 (the surface) and
$r_{s}$
, respectively. It was found, as in Ramachandran (Reference Ramachandran2002), Young et al. (Reference Young, Tsai, Chen and Fan2008) and Lockerby & Collyer (Reference Lockerby and Collyer2016), that faster convergence to the analytic solutions was obtained when the singularities were furthest from the computational domain
$r_{s}\ll 1$
, but that this can lead to ill-conditioning. A compromise of
$r_{s}=0.1$
was found to work well and was used in all that follows. For the R13-MFS solver, the number of nodes was chosen to be 102, with further increases giving results that were graphically indistinguishable. Notably, at low
$\mathit{Kn}$
, R13 requires more nodes than G13 in order to resolve sharp exponentially decaying Knudsen layers.
5.2 Heat transfer from a stationary sphere
We consider a stationary sphere (
$\boldsymbol{v}^{w}=\mathbf{0}$
) whose temperature (
$\unicode[STIX]{x1D703}^{w}$
) is maintained above that of the far field (
$\unicode[STIX]{x1D703}\rightarrow 0$
as
$r\rightarrow \infty$
); see figure 1(a) with
$\unicode[STIX]{x1D703}^{w}=1$
and
$U_{\infty }=0$
. In a spherical coordinate system (
$r$
,
$\unicode[STIX]{x1D6FC}$
,
$\unicode[STIX]{x1D719}$
), because of the spherical symmetry, the flow properties are independent of the azimuthal and polar directions. Accordingly, all non-zero components can be expressed in terms of the temperature
$\unicode[STIX]{x1D703}(r)$
, radial heat flux
$q_{r}(r)$
and radial–radial deviatoric stress
$\unicode[STIX]{x1D61A}_{rr}(r)$
. The analytic expressions for these quantities are obtained from (2.1)–(2.2) as
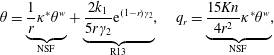$$\begin{eqnarray}\unicode[STIX]{x1D703}=\underbrace{\frac{1}{r}\unicode[STIX]{x1D705}^{\ast }\unicode[STIX]{x1D703}^{w}}_{\text{NSF}}+\underbrace{\frac{2k_{1}}{5r\unicode[STIX]{x1D6FE}_{2}}\text{e}^{(1-r)\unicode[STIX]{x1D6FE}_{2}}}_{\text{R13}},\quad q_{r}=\underbrace{\frac{15\mathit{Kn}}{4r^{2}}\unicode[STIX]{x1D705}^{\ast }\unicode[STIX]{x1D703}^{w}}_{\text{NSF}},\end{eqnarray}$$
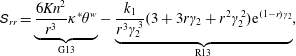$$\begin{eqnarray}\unicode[STIX]{x1D61A}_{rr}=\underbrace{\frac{6\mathit{Kn}^{2}}{r^{3}}\unicode[STIX]{x1D705}^{\ast }\unicode[STIX]{x1D703}^{w}}_{\text{G13}}-\underbrace{\frac{k_{1}}{r^{3}\unicode[STIX]{x1D6FE}_{2}^{3}}(3+3r\unicode[STIX]{x1D6FE}_{2}+r^{2}\unicode[STIX]{x1D6FE}_{2}^{2})\text{e}^{(1-r)\unicode[STIX]{x1D6FE}_{2}}}_{\text{R13}},\end{eqnarray}$$
where
$\unicode[STIX]{x1D705}^{\ast }$
(effective heat conductivity) and
$k_{1}$
are constants of integration. The macroscopic quantities in (5.1)–(5.2) are superpositions of NSF contributions (first order in
$\mathit{Kn}$
), G13 contributions (second order in
$\mathit{Kn}$
) and from R13 exponential functions describing Knudsen layers. It should be noted that for the NSF and G13 solutions, terms with
$k_{1}$
are absent; therefore, only one boundary condition is required (to fix
$\unicode[STIX]{x1D705}^{\ast }$
). For example, if the no temperature-jump condition is specified at the boundary (i.e.
$\unicode[STIX]{x1D703}=\unicode[STIX]{x1D703}^{w}$
), then
$\unicode[STIX]{x1D705}^{\ast }=1$
, but this is known to only be valid for
$\mathit{Kn}\rightarrow 0$
. In the free-molecular case of
$\mathit{Kn}\rightarrow \infty$
, the effective heat conductivity
$\unicode[STIX]{x1D705}^{\ast }=0$
. For intermediate
$\mathit{Kn}$
, the constants of integration are calculated analytically using the appropriate boundary conditions (2.5), to give
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D705}^{\ast }=\frac{3597.49+17\,472.4\,\mathit{Kn}+37\,707.3\,\mathit{Kn}^{2}+33\,899\,\mathit{Kn}^{3}}{3597.49+26\,102.9\,\mathit{Kn}+97\,174.2\,\mathit{Kn}^{2}+199\,068\,\mathit{Kn}^{3}+196\,516\,\mathit{Kn}^{4}+108\,961\,\mathit{Kn}^{5}},\hspace{-6.0pt} & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \!\!\displaystyle k_{1}=\frac{1074.49+14\,696.9\,\mathit{Kn}+51\,575.7\,\mathit{Kn}^{2}}{3597.49+26\,102.9\,\mathit{Kn}+97\,174.2\,\mathit{Kn}^{2}+199\,068\,\mathit{Kn}^{3}+196\,516\,\mathit{Kn}^{4}+108\,961\,\mathit{Kn}^{5}}\unicode[STIX]{x1D703}^{w}.\hspace{-6.0pt} & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
Figure 1(b) shows the variation in
$\unicode[STIX]{x1D705}^{\ast }$
with
$\mathit{Kn}$
, showing that the R13-MFS agrees perfectly with the R13 analytic solution and that these are close, in contrast to the NSF, to the linearised Boltzmann equation (LBE) solutions. While the classical NSF with no jump is within 5 % of the LBE solution only up to
$\mathit{Kn}=0.02$
, R13 maintains this accuracy up to
$\mathit{Kn}=0.5$
.
5.3 Flow around a stationary sphere
We consider a sphere moving relative to the fluid with dimensionless speed 1 at a temperature equal to the far-field value
$\unicode[STIX]{x1D703}^{w}=0$
, and sit in the frame moving with the sphere (see figure 1
a with
$\unicode[STIX]{x1D703}^{w}=0$
and
$U_{\infty }=1$
). The most natural coordinate system is cylindrical polars with the
$z$
-axis in the direction of the uniform far-field velocity,
$\unicode[STIX]{x1D6FC}$
the polar angle and
$\unicode[STIX]{x1D719}$
the azimuthal angle about which axisymmetry is assumed. For this problem, an analytic solution was derived for R13 by Torrilhon (Reference Torrilhon2010).
As can be seen in figure 2(a), at higher
$\mathit{Kn}$
, the disturbance to the uniform flow caused by the sphere is significantly reduced. This is confirmed in figure 3(a), where the polar velocity at the midpoint,
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/2$
, is shown to barely deviate from the free stream speed of
$-1$
at higher
$\mathit{Kn}$
, in contrast to the behaviour at lower
$\mathit{Kn}$
, where no slip,
$v_{\unicode[STIX]{x1D6FC}}(r=1)=0$
, is approached and the bulk flow is significantly disturbed. Notably, our R13-MFS predictions in figure 3 are shown to agree perfectly with the analytic results. (It should be noted that the analytic results for temperature were obtained by a code provided by Torrilhon, updated since 2010.)
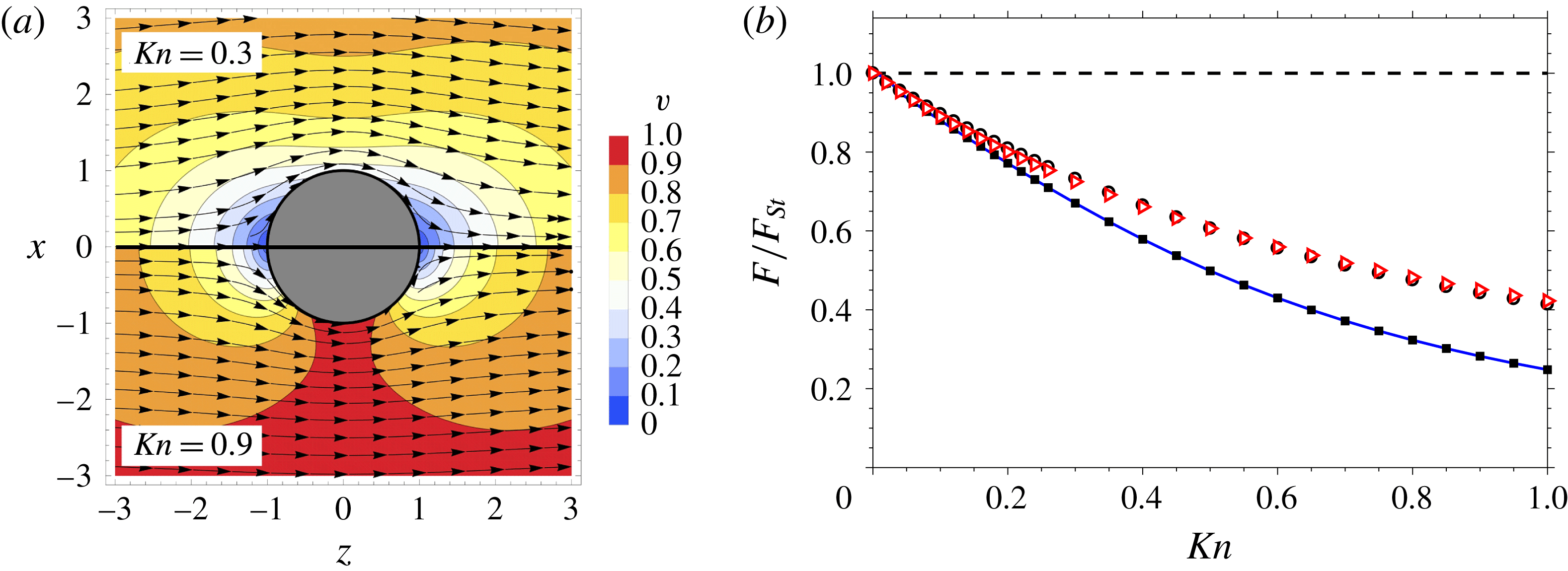
Figure 2. (a) The velocity streamlines and speed contours for a sphere embedded in a uniform flow (in the plane
$y=0$
) at two values of
$\mathit{Kn}$
. (b) The drag force normalised by the Stokes flow drag prediction,
$F_{St}=6\unicode[STIX]{x03C0}a^{2}\mathit{Kn}\,U_{\infty }$
(– – –), compared with experiments (○) (Allen & Raabe Reference Allen and Raabe1982), R13-MFS (▪), R13 analytic predictions (——) and kinetic theory solutions (▹) collated in Bailey et al. (Reference Bailey, Barber, Emerson, Lockerby and Reese2005).
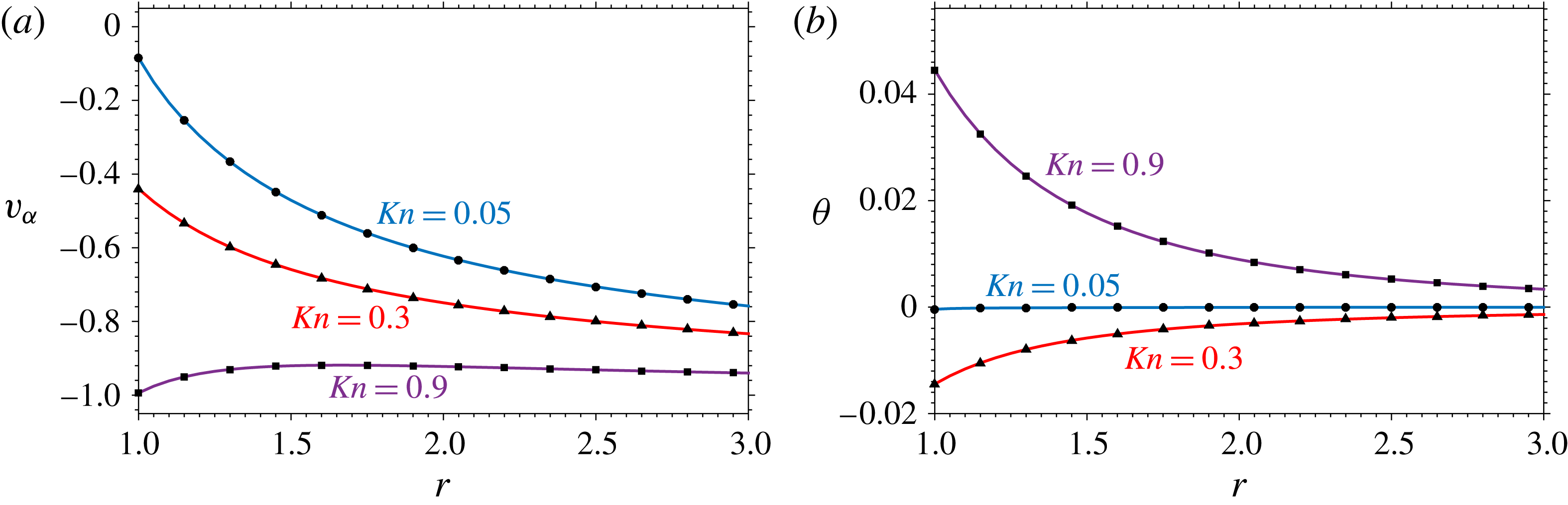
Figure 3. The polar velocity
$v_{\unicode[STIX]{x1D6FC}}$
at
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/2$
and temperature
$\unicode[STIX]{x1D703}$
at
$\unicode[STIX]{x1D6FC}=0$
for flow around a sphere. The R13-MFS predictions (●, ▴, ▪) for
$\mathit{Kn}=0.05,0.3,0.9$
respectively compared with the analytic result from Torrilhon (Reference Torrilhon2010) (solid lines).
Comparisons of the drag force on the sphere, in figure 2(b), show that the R13-MFS prediction (i) agrees with the analytic solution and (ii) provides a better agreement with experimental results from Millikan (Reference Millikan1923) (fitted by Allen & Raabe Reference Allen and Raabe1982), aligning with kinetic theory solutions (Sone & Aoki Reference Sone and Aoki1977; Beresnev, Chernyak & Fomyagin Reference Beresnev, Chernyak and Fomyagin1990), than NSF is able to. The R13 is within 10 % of the experimental data up to
$\mathit{Kn}=0.39$
, compared with the NSF, which fails at
$\mathit{Kn}=0.11$
.
As discussed in detail in Torrilhon (Reference Torrilhon2010), in contrast to the NSF, the R13 system also predicts temperature variations, as also observed in kinetic solutions (Takata, Sone & Aoki Reference Takata, Sone and Aoki1993) due to the cross-coupling of stress and heat flux. The same temperature polarisation as seen in Torrilhon (Reference Torrilhon2010) has been observed, as shown in figure 3(b): at
$\mathit{Kn}=0.3$
the temperature is negative where the flow leaves the sphere (and positive where it approaches), in qualitative agreement with kinetic solutions.
5.4 Hydrodynamic interactions between approaching solid spheres
To demonstrate the potential of our new method, we consider how the quasistatic hydrodynamic interaction between two equal-sized spheres each moving with unit speed towards the other, along their lines of centre, depends on the distance between their centres
$l$
(which could be used to define a second Knudsen number of interest) and
$\mathit{Kn}$
(see figure 4
a). Calculation of the induced force on neighbouring spheres is key to the dynamics of particulate flows, and the Knudsen number associated with such flows is often in the transition regime, meaning that traditional approaches, e.g. that of Happel & Brenner (Reference Happel and Brenner1965), become inaccurate.
Figure 4(b) shows that as
$\mathit{Kn}\rightarrow 0$
, R13 and G13 approach a common limit, and that limit, reassuringly, at larger separations (
$l=10$
), agrees with the analytic result in Happel & Brenner (Reference Happel and Brenner1965) obtained for the NSF. However, even at moderate
$\mathit{Kn}$
, G13 dramatically overpredicts the force on a sphere compared with R13. Taking the
$l=10$
case as an example, at
$\mathit{Kn}=0.5$
, G13 predicts
$F/\mathit{Kn}=15.01$
while the R13 prediction is
$F/\mathit{Kn}=10.16$
, giving an overprediction of 47.7 %. The NSF result is far worse, being insensitive to
$\mathit{Kn}$
, and figure 4(a) indicates that this occurs because at higher
$\mathit{Kn}$
the spheres disturb the flow less, so that their interaction forces are reduced.
Although this particular set-up happens to be axisymmetric, the method can, at no additional computational cost, obtain the interaction forces for all possible three-dimensional configurations in order to, for example, provide the microscopic information required for the construction of macroscopic particulate flow models.
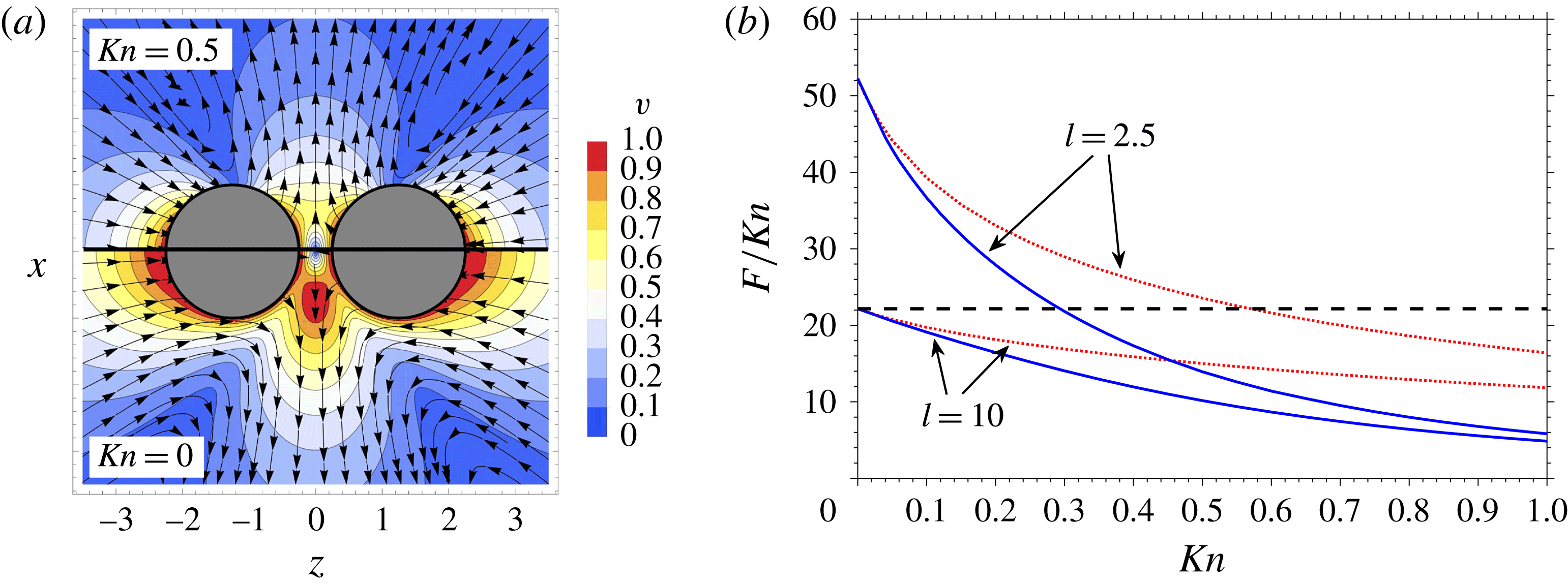
Figure 4. (a) The quasistatic flow field (speed contours and velocity streamlines) for R13 at
$\mathit{Kn}=0.5$
and
$\mathit{Kn}=0$
(i.e. NSF) generated by two spheres approaching each other with relative speed
$U=2$
. (b) The drag force generated on one of the spheres at two different separations. The force predicted by R13-MFS (——) is compared with G13-MFS predictions (
$\cdots \cdots$
). As
$Kn\rightarrow 0$
, the curves for each separation approach a value corresponding to the
$Kn$
-independent NSF solution. For large separations (
$l=10$
here), this value is close to the analytic solution (horizontal dashed line) derived in Happel & Brenner (Reference Happel and Brenner1965).
6 Discussion
The derivation of the R13 fundamental solutions represents just the first step in a programme of research whose possibilities are outlined below.
6.1 Exploitation of the R13-MFS
Within this article, the full potential for the new computational tool has only been touched upon, as our focus here was on methodology and benchmarking. The R13-MFS has been shown to describe fully three-dimensional flows that include non-equilibrium gas effects in an incredibly efficient manner, giving it a significant advantage for flows in the range
$\mathit{Kn}\approx 0.01$
–0.5 over traditional methods such as DSMC, which can become computationally intensive for small-Mach-number flows. This range includes numerous physical systems characterised by scales
$\hat{L}=0.1{-}7~\unicode[STIX]{x03BC}\text{m}$
at atmospheric pressure, and larger at reduced pressure, e.g. for recent applications in free surface flows (Sprittles Reference Sprittles2017). Of initial interest are canonical flow problems, studied intensively for Stokes flow, including solid objects of various shapes in classical flows (shear, extensional, etc.) which will provide insight into possible effects in more complex phenomena (e.g. particulate flows).
6.2 Extension to higher orders
The R13 system is the lowest-order set of regularised moments that captures some basic features of the Knudsen layer. For Kramer’s problem of shear flow past a plate, it is known that R13 predicts the existence of one exponential decay rate to capture the behaviour of the layer. In reality, the Knudsen layer is formed from the superposition of many such exponential functions, so that approximation of this behaviour with one function can lead to poor accuracy as
$\mathit{Kn}$
is increased. This was part of the motivation for developing the R26 system in Gu & Emerson (Reference Gu and Emerson2009, Reference Gu and Emerson2014), where three exponential functions are superimposed to form the Knudsen layer and significantly better accuracy is achieved in comparison with benchmark linearised Boltzmann solutions. These advantages of R26 appear to be sufficient to render an attempt to derive fundamental solutions worthwhile.
It should be noted that while the complexity of the R13 fundamental solutions is a step up from those obtained for NSF and G13, once these solutions have been obtained and implemented into a numerical approach, the reduction in computational cost compared with other approaches more than compensates the initial investment. It is likely that the same will be true for the R26 system, where the approach developed here should also apply once a deeper understanding of the structure of the fundamental solutions for higher-order moment equations emerges. Looking further into the future, one may look to automate the process of deriving higher-order fundamental solutions so that one can pick the correct number of moments for a given problem; i.e. use the m-refinement suggested by Torrilhon & Sarna (Reference Torrilhon and Sarna2017).
Acknowledgements
The authors thank M. Torrilhon for invaluable advice and for access to his Mathematica script containing the explicit solution obtained in Torrilhon (Reference Torrilhon2010). The work was supported by the EPSRC (grants EP/N016602/1, EP/P020887/1, EP/K038664/1 and EP/P031684/1) and the Leverhulme Trust (Research Project Grant).
Open access
