Article contents
Genesis and evolution of velocity gradients in near-field spatially developing turbulence
Published online by Cambridge University Press: 20 February 2017
Abstract
This paper investigates the dynamics of velocity gradients for a spatially developing flow generated by a single square element of a fractal square grid at low inlet Reynolds number through direct numerical simulation. This square grid-element is also the fundamental block of a classical grid. The flow along the grid-element centreline is initially irrotational and becomes turbulent further downstream due to the lateral excursions of vortical turbulent wakes from the grid-element bars. We study the generation and evolution of the symmetric and anti-symmetric parts of the velocity gradient tensor for this spatially developing flow using the transport equations of mean strain product and mean enstrophy respectively. The choice of low inlet Reynolds number allows for fine spatial resolution and long simulations, both of which are conducive in balancing the budget equations of the above quantities. The budget analysis is carried out along the grid-element centreline and the bar centreline. The former is observed to consist of two subregions: one in the immediate lee of the grid-element which is dominated by irrotational strain, and one further downstream where both strain and vorticity coexist. In the demarcation area between these two subregions, where the turbulence is inhomogeneous and developing, the energy spectrum exhibits the best 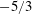 $-5/3$ power-law slope. This is the same location where the experiments at much higher inlet Reynolds number show a well-defined
$-5/3$ power-law slope. This is the same location where the experiments at much higher inlet Reynolds number show a well-defined 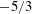 $-5/3$ spectrum over more than a decade of frequencies. Yet, the
$-5/3$ spectrum over more than a decade of frequencies. Yet, the 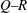 $Q{-}R$ diagram, where
$Q{-}R$ diagram, where 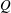 $Q$ and
$Q$ and 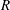 $R$ are the second and third invariants of the velocity gradient tensor, remains undeveloped in the near-grid-element region, and both the intermediate and extensive strain-rate eigenvectors align with the vorticity vector. Along the grid-element centreline, the strain is the first velocity gradient quantity generated by the action of pressure Hessian. This strain is then transported downstream by fluctuations and strain self-amplification is activated a little later. Further downstream, vorticity from the bar wakes is brought towards the grid-element centreline, and, through the interaction with strain, leads to the production of enstrophy. The strain-rate tensor has a statistically axial stretching form in the production region, but a statistically biaxial stretching form in the decay region. The usual signatures of velocity gradients such as the shape of
$R$ are the second and third invariants of the velocity gradient tensor, remains undeveloped in the near-grid-element region, and both the intermediate and extensive strain-rate eigenvectors align with the vorticity vector. Along the grid-element centreline, the strain is the first velocity gradient quantity generated by the action of pressure Hessian. This strain is then transported downstream by fluctuations and strain self-amplification is activated a little later. Further downstream, vorticity from the bar wakes is brought towards the grid-element centreline, and, through the interaction with strain, leads to the production of enstrophy. The strain-rate tensor has a statistically axial stretching form in the production region, but a statistically biaxial stretching form in the decay region. The usual signatures of velocity gradients such as the shape of 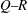 $Q{-}R$ diagrams and the alignment of vorticity vector with the intermediate eigenvector are detected only in the decay region even though the local Reynolds number (based on the Taylor length scale) is only between 30 and 40.
$Q{-}R$ diagrams and the alignment of vorticity vector with the intermediate eigenvector are detected only in the decay region even though the local Reynolds number (based on the Taylor length scale) is only between 30 and 40.
Information
- Type
- Papers
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 37
- Cited by


