Hostname: page-component-cb9f654ff-c75p9 Total loading time: 0 Render date: 2025-08-01T07:11:44.427Z Has data issue: false hasContentIssue false
  • English
  • Français

A geometrical Green–Naghdi-type system for dispersive-like waves in prismatic channels

Published online by Cambridge University Press:  26 June 2025

Sergey Gavrilyuk Open the ORCID record for Sergey Gavrilyuk [Opens in a new window]  and
Mario Ricchiuto Open the ORCID record for Mario Ricchiuto [Opens in a new window]
Sergey Gavrilyuk
Affiliation:
Aix Marseille Université, CNRS, IUSTI, UMR 7343, Marseille, France
Mario Ricchiuto*
Affiliation:
INRIA, Univ. Bordeaux, CNRS, Bordeaux INP, IMB, UMR 5251, 200 Avenue de la Vieille Tour, Talence CEDEX 33405, France
*
Corresponding author: Mario Ricchiuto, mario.ricchiuto@inria.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

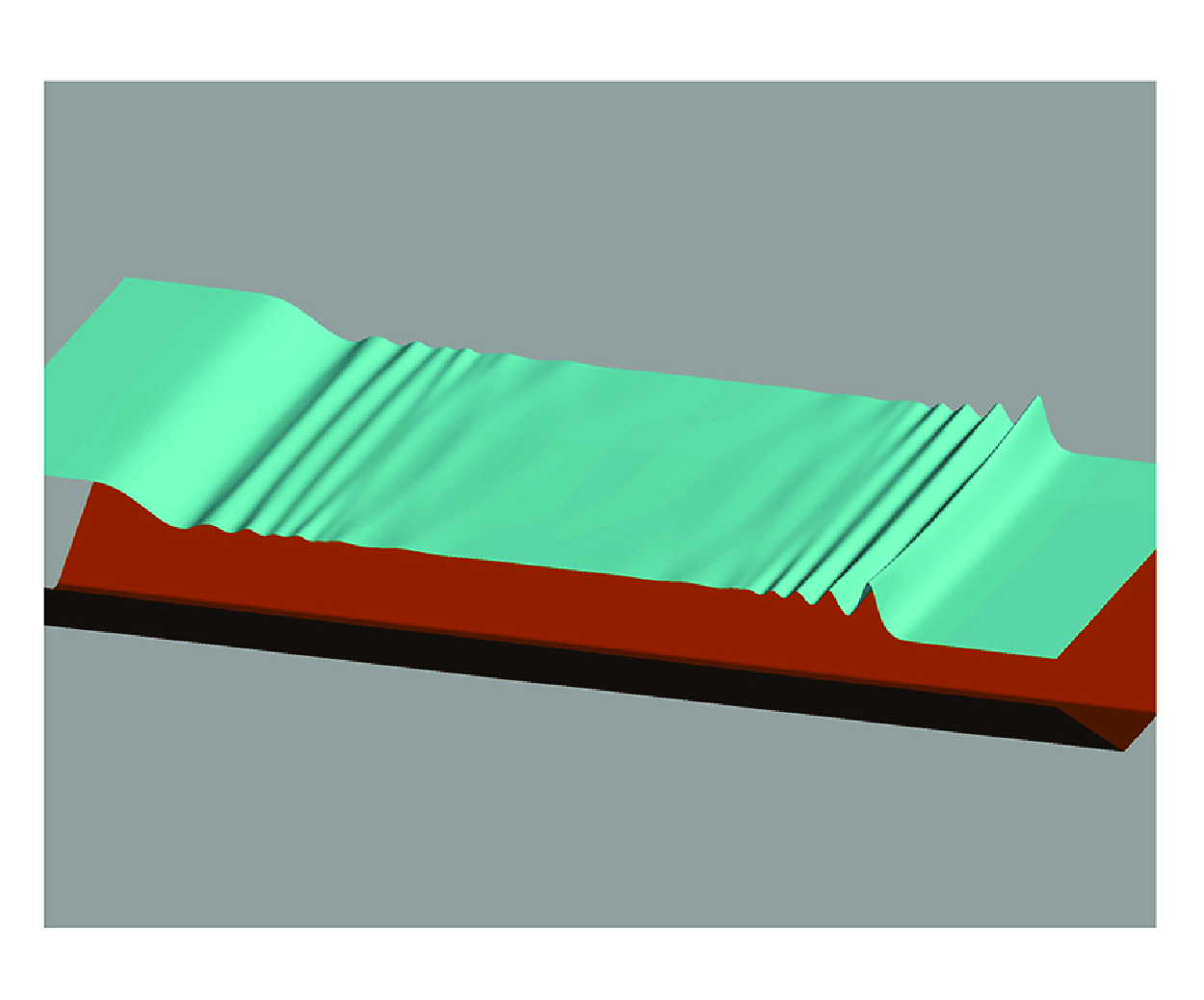
We consider two-dimensional (2-D) free surface gravity waves in prismatic channels, including bathymetric variations uniquely in the transverse direction. Starting from the Saint-Venant equations (shallow-water equations) we derive a one-dimensional transverse averaged model describing dispersive effects related solely to variations of the channel topography. These effects have been demonstrated in Chassagne et al. 2019 J. Fluid Mech. 870, 595–616 to be predominant in the propagation of bores with Froude numbers below a critical value of approximately 1.15. The model proposed is fully nonlinear, Galilean invariant, and admits a variational formulation under natural assumptions about the channel geometry. It is endowed with an exact energy conservation law, and admits exact travelling-wave solutions. Our model generalises and improves the linear equations proposed by Chassagne et al. 2019 J. Fluid Mech. 870, 595–616, as well as in Quezada de Luna and Ketcheson, 2021 J. Fluid Mech. 917, A45. The system is recast in two useful forms appropriate for its numerical approximations, whose properties are discussed. Numerical results allow the verification of the implementation of these formulations against analytical solutions, and validation of our model against fully 2-D nonlinear shallow-water simulations, as well as the famous experiments by Treske 1994 J. Hyd. Res. 32, 355–370.

JFM classification

Geophysical and Geological Flows: Shallow water flows Waves/Free-surface Flows: Channel flow Waves/Free-surface Flows: Surface gravity waves

Information

Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 1014 , 10 July 2025 , A5
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Abgrall, R. & Ricchiuto, M. 2017 High order methods for CFD. In Encyclopedia of Computational Mechanics, Second Edition (ed. R.de Borst E. Stein & T.J.R. Hughes), pp. 1–54. John Wiley and Sons.Google Scholar
Abgrall, R. & Ricchiuto, M. 2022 Hyperbolic balance laws: residual distribution, local and global fluxes. In Numerical Fluid Dynamics: Methods and Computations (ed. D. Zeidan, J. Merker, E. Goncalves Da Silva & L.T. Zhang), pp. 177–222. Springer Nature Singapore.CrossRefGoogle Scholar
Arpaia, L. & Ricchiuto, M. 2018 r − adaptation for Shallow Water flows: conservation, well balancedness, efficiency. Comput. Fluids 160, 175–203.CrossRefGoogle Scholar
Arpaia, L. & Ricchiuto, M. 2020 Well balanced residual distribution for the ALE spherical shallow water equations on moving adaptive meshes. J. Comput. Phys. 405, 109173.CrossRefGoogle Scholar
Berezovski, A., Engelbrecht, J. & Berezovski, M. 2011 Waves in microstructured solids: a unified viewpoint of modeling. Acta Mechanica 220 (1–4), 349–363.CrossRefGoogle Scholar
Berezovski, A., Engelbrecht, J., Salupere, A., Tamm, K., Peets, T. & Berezovski, M. 2013 Dispersive waves in microstructured solids. Intl J. Solids Struct. 50 (11), 1981–1990.CrossRefGoogle Scholar
Bonneton, N., Bonneton, P., Parisot, J.-P., Sottolichio, A. & Detandt, G. 2012 Ressaut de marée et Mascaret – exemples de la Garonne et de la Seine. Comptes Rendus Geosciences 344 (10), 508–515.CrossRefGoogle Scholar
Bonneton, P., Bonneton, N., Parisot, J.-P. & Castelle, B. 2015 Tidal bore dynamics in funnel-shaped estuaries. J. Geophys. Res.: Oceans 120 (2), 923–941.CrossRefGoogle Scholar
Bonneton, P., Chazel, F., Lannes, D., Marche, F. & Tissier, M. 2011 A splitting approach for the fully nonlinear and weakly dispersive Green–Naghdi model. J. Comput. Phys. 230 (4), 1479–1498.CrossRefGoogle Scholar
Busto, S., Dumbser, M., Escalante, C., Favrie, N. & Gavrilyuk, S. 2021 On high order ADER discontinuous Galerkin schemes for first order hyperbolic reformulations of nonlinear dispersive systems. J. Sci. Comput. 87 (2), 1–47.CrossRefGoogle Scholar
Cauquis, A., Ricchiuto, M. & Heinrich, P. 2022 Lax–wendroff schemes with polynomial extrapolation and simplified lax–wendroff schemes for dispersive waves: a comparative study. Water Waves 4 (3), 1–33.CrossRefGoogle Scholar
Chassagne, R., Filippini, A.G., Ricchiuto, M. & Bonneton, P. 2018 Dispersive and dispersive-like bores in channels with sloping banks. Research Report RR-9228, Inria Bordeaux Sud-Ouest.CrossRefGoogle Scholar
Chassagne, R., Filippini, A.G., Ricchiuto, M. & Bonneton, P. 2019 Dispersive and dispersive-like bores in channels with sloping banks. J. Fluid Mech. 870, 595–616.CrossRefGoogle Scholar
Dhaouadi, F., Favrie, N. & Gavrilyuk, S. 2019 Extended Lagrangian approach for the defocusing nonlinear Schrödinger equation. Stud. Appl. Math. 142 (3), 336–358.CrossRefGoogle Scholar
Duchêne, V. 2019 Rigorous justification of the Favrie–Gavrilyuk approximation to the Serre–Green–Naghdi model. Nonlinearity 32 (10), 3772–3797.CrossRefGoogle Scholar
Dumbser, M., Balsara, D.S., Toro, E.F. & Munz, C.-D. 2008 A unified framework for the construction of one-step finite volume and discontinuous Galerkin schemes on unstructured meshes. J. Comput. Phys. 227 (18), 8209–8253.CrossRefGoogle Scholar
Favre, H. 1935 Etude théorique et Expérimentale Des Ondes De Translation Dans Les Canaux découverts. Dunod.Google Scholar
Favrie, N. & Gavrilyuk, S. 2017 A rapid numerical method for solving Serre–Green–Naghdi equations describing long free surface gravity waves. Nonlinearity 30 (7), 2718–2736.CrossRefGoogle Scholar
Filippini, A.G., Kazolea, M. & Ricchiuto, M. 2016 A flexible genuinely nonlinear approach for nonlinear wave propagation, breaking and run-up. J. Comput. Phys. 310, 381–417.CrossRefGoogle Scholar
Gavrilyuk, S. 2011 Multiphase flow modeling via Hamilton’s principle. In Variational Models and Methods in Solid and Fluid Mechanics (ed. F. dell’Isola & S. Gavrilyuk), pp. 163–210. Springer Vienna.CrossRefGoogle Scholar
Gavrilyuk, S., Nkonga, B., Shyue, K.-M. & Truskinovsky, L. 2020 Stationary shock-like transition fronts in dispersive systems. Nonlinearity 33 (10), 5477–5509.CrossRefGoogle Scholar
Gavrilyuk, S. & Shyue, K.-M. 2021 Singular solutions of the BBM equation: analytical and numerical study. Nonlinearity 35 (1), 388–410.CrossRefGoogle Scholar
Gavrilyuk, S. & Shyue, K.-M. 2024 2D Serre–Green–Naghdi Equations over Topography: Elliptic Operator Inversion Method. J. Hydraul. Engng 150 (1), 04023054.CrossRefGoogle Scholar
Jouy, B., Violeau, D., Ricchiuto, M. & Le, M. 2024 One dimensional modelling of Favre waves in channels. Appl. Math. Model. 133, 170–194.CrossRefGoogle Scholar
Kazolea, M., Filippini, A.G. & Ricchiuto, M. 2023 Low dispersion finite volume/element discretization of the enhanced Green–Naghdi equations for wave propagation, breaking and runup on unstructured meshes. Ocean Model. 182, 102157.CrossRefGoogle Scholar
Ketcheson, D. & Quezada de Luna, M. 2015 Diffractons: solitary waves created by diffraction in periodic media. Multiscale Model. Simul. 13 (1), 440–458.CrossRefGoogle Scholar
Ketcheson, D.I. & Russo, G. 2024 A dispersive effective equation for transverse propagation of planar shallow water waves over periodic bathymetry. arXiv: 2409.00076.CrossRefGoogle Scholar
Le Métayer, O., Gavrilyuk, S. & Hank, S. 2010 A numerical scheme for the Green–Naghdi model. J. Comput. Phys. 229 (6), 2034–2045.CrossRefGoogle Scholar
Lemoine, R. 1948 Notules hydrauliques. La Houille Blanche 2, 183–186.Google Scholar
Quezada de Luna, M. & Ketcheson, D.I. 2021 Solitary water waves created by variations in bathymetry. J. Fluid Mech. 917, A45.CrossRefGoogle Scholar
Mazaheri, A., Ricchiuto, M. & Nishikawa, H. 2016 A first-order hyperbolic system approach for dispersion. J. Comput. Phys. 321, 593–605.CrossRefGoogle Scholar
Michel-Dansac, V., Noble, P. & Vila, J.-P. 2021 Consistent section-averaged shallow water equations with bottom friction. Eur. J. Mech. - B/Fluids 86, 123–149.CrossRefGoogle Scholar
Parisot, M. 2019 Entropy-satisfying scheme for a hierarchy of dispersive reduced models of free surface flow. Intl J. Numer. Meth. Flow 91 (10), 509–531.CrossRefGoogle Scholar
Peregrine, D.H. 1968 Long waves in a uniform channel of arbitrary cross-section. J. Fluid Mech. 32 (2), 353–365.CrossRefGoogle Scholar
Ranocha, H. & Ricchiuto, M. 2024 Structure-preserving approximations of the Serre–Green–Naghdi equations in standard and hyperbolic form. arXiv: 2408.02665.CrossRefGoogle Scholar
Ricchiuto, M. 2011 Contributions to the development of residual discretizations for hyperbolic conservation laws with application to shallow water flows. In Habilitation à Diriger Des Recherches, Université Sciences et Technologies - Bordeaux I.Google Scholar
Ricchiuto, M. 2015 An explicit residual based approach for shallow water flows. J. Comput. Phys. 280, 306–344.CrossRefGoogle Scholar
Teng, M.H. & Wu, T.Y. 1992 Nonlinear water waves in channels of arbitrary shape. J. Fluid Mech. 242, 211–233.CrossRefGoogle Scholar
Teng, M.H. & Wu, T.Y. 1997 Effects of channel cross-sectional geometry on long wave generation and propagation. Phys. Fluids 9 (11), 3368–3377.CrossRefGoogle Scholar
Tkachenko, S., Gavrilyuk, S. & Massoni, J. 2023 Extended Lagrangian approach for the numerical study of multidimensional dispersive waves: applications to the Serre–Green–Naghdi equations. J. Comput. Phys. 477, 111901.CrossRefGoogle Scholar
Torlo, D. & Ricchiuto, M. 2023 Model order reduction strategies for weakly dispersive waves. Maths Comput. Simul. 205, 997–1028.CrossRefGoogle Scholar
Treske, A. 1994 Undular bores (Favre-waves) in open channels - experimental studies. J. Hydraul. Res. 32 (3), 355–370.CrossRefGoogle Scholar
Wei, G., Kirby, J.T., Grilli, S.T. & Subramanya, R. 1995 A fully nonlinear Boussinesq model for surface waves. Part 1. Highly nonlinear unsteady waves. J. Fluid Mech. 294, 71–92.CrossRefGoogle Scholar
Winckler, P. & Liu, P.L.-F. 2015 Long waves in a straight channel with non-uniform cross-section. J. Fluid Mech. 770, 156–188.CrossRefGoogle Scholar