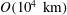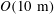1 Introduction
In 1802 the Austrian physicist and engineer Franz Josef von Gerstner published a remarkable solution to the water-wave problem, remarkable because his solution, obtained through consideration of the Lagrangian equations of motion, is an exact solution to the Euler equation with a free boundary – see Gerstner (Reference Gerstner1802); the solution was rediscovered by Froude (Reference Froude1862) and Rankine (Reference Rankine1863). In contrast, Stokes’ solution published 45 years later only approximately satisfies the free surface condition; see Stokes (Reference Stokes1847). As argued by Lamb (Reference Lamb1932), because the Gerstner flow is rotational, it cannot be generated by conservative forces and so has largely been neglected in the literature. However, there exist observations that do suggest the possibility of Gerstner waves: Monismith et al. (Reference Monismith, Nepf, Cowen, Thais and Magnaudet2007) report laboratory experiments for which mean (wave-averaged) Eulerian flows exactly cancelled the Stokes drift, behaviour that is the lowest-order observable difference between Gerstner and higher-order (nonlinear) Stokes waves. Besides their own experiments, Monismith et al. (Reference Monismith, Nepf, Cowen, Thais and Magnaudet2007) showed that other experiments, notably those of Swan (Reference Swan1990), also displayed this behaviour, although other work in the same flume reported in Swan & Sleath (Reference Swan and Sleath1990) showed mean velocity profiles that agreed better with higher-order Stokes wave theory. Weber (Reference Weber2011) developed a surface boundary layer theory including surface tension for both Stokes and Gerstner waves, and compared the results to laboratory experiments of Law (Reference Law1999). Objective examination of his results suggests that both theories are of nearly equal accuracy.
The necessity of mean Eulerian flows that cancel the Stokes drift has also been suggested by Ursell (Reference Ursell1950) and Hasselmann (Reference Hasselmann1970), both of whom examined wave propagation on a rotating Earth. In particular, Hasselmann showed that at steady state, there would be a wave-averaged force directed along wave crests (that is, perpendicular to the wave propagation direction) due to distortion of the planetary vorticity by the waves. The so-called Hasselmann force (see e.g. Lentz et al.
Reference Lentz, Fewings, Howd, Fredericks and Hathaway2008) represents the strong rotation limit of the vortex force identified by Craik & Leibovich (Reference Craik and Leibovich1976) that arises from interaction of the wave velocity field with the mean vorticity field, in this case associated with the vertical vorticity (which is nearly equal to the planetary vorticity,
![]() $\mathfrak{f}$
) and the horizontal, depth-variable Stokes drift.
$\mathfrak{f}$
) and the horizontal, depth-variable Stokes drift.
Pollard (Reference Pollard1970) derived an extension of Gerstner’s theory applicable to rotating flows, showing that for gravity waves, the effect was a very slight (1 part in
![]() $10^{4}$
) correction in the dispersion relation, and a very slight cross-wave tilt to wave orbital motions. Pollard noted however the important aspect of this solution: it satisfies Hasselmann’s mean flow constraint; i.e. as with other Gerstner-type wave motions (e.g. Constantin Reference Constantin2001, Reference Constantin2012; Hsu Reference Hsu2015; Henry Reference Henry2016a
), particle trajectories are closed. Moreover, like non-rotating Gerstner waves, the difference between Stokes waves and Pollard’s wave is only apparent in a change in the mean flow at second order in wave slope, a difference that is difficult to discern observationally although there are suggestions for such a difference in the literature, notably simultaneous ocean observations of Eulerian and Lagrangian motions reported by Smith (Reference Smith2006). Xu & Bowen (Reference Xu and Bowen1994) used an approximate, linear Eulerian analysis to show that because motions parallel to wave crests are in phase with vertical velocities, there is a weak wave stress. In the absence of viscosity, this wave stress produces the same steady Eulerian mean flow that Pollard found for Coriolis-affected Gerstner waves. However, the observations of Smith (Reference Smith2006) point to a second weakness of Gerstner wave theory: no one has developed a theory for Gerstner wave groups or has proved that such groups can exist. Indeed, the generation of the Stokes drift cancellation via the Hasselmann force presumably requires a time that is comparable to the inertial period (cf. the discussion in Pollard (Reference Pollard1970) or Xu & Bowen (Reference Xu and Bowen1994)), and thus is not likely to be applicable to wave group dynamics. Nonetheless, while there are no known solutions to initial value problems that produce Gerstner waves, neither has it been proven that such solutions do not exist. At the same time, we are unaware of any explanation based on Stokes wave theory that can describe Smith’s observations that mean Eulerian flows developed that cancelled the Stokes drift associated with passing wave groups.
$10^{4}$
) correction in the dispersion relation, and a very slight cross-wave tilt to wave orbital motions. Pollard noted however the important aspect of this solution: it satisfies Hasselmann’s mean flow constraint; i.e. as with other Gerstner-type wave motions (e.g. Constantin Reference Constantin2001, Reference Constantin2012; Hsu Reference Hsu2015; Henry Reference Henry2016a
), particle trajectories are closed. Moreover, like non-rotating Gerstner waves, the difference between Stokes waves and Pollard’s wave is only apparent in a change in the mean flow at second order in wave slope, a difference that is difficult to discern observationally although there are suggestions for such a difference in the literature, notably simultaneous ocean observations of Eulerian and Lagrangian motions reported by Smith (Reference Smith2006). Xu & Bowen (Reference Xu and Bowen1994) used an approximate, linear Eulerian analysis to show that because motions parallel to wave crests are in phase with vertical velocities, there is a weak wave stress. In the absence of viscosity, this wave stress produces the same steady Eulerian mean flow that Pollard found for Coriolis-affected Gerstner waves. However, the observations of Smith (Reference Smith2006) point to a second weakness of Gerstner wave theory: no one has developed a theory for Gerstner wave groups or has proved that such groups can exist. Indeed, the generation of the Stokes drift cancellation via the Hasselmann force presumably requires a time that is comparable to the inertial period (cf. the discussion in Pollard (Reference Pollard1970) or Xu & Bowen (Reference Xu and Bowen1994)), and thus is not likely to be applicable to wave group dynamics. Nonetheless, while there are no known solutions to initial value problems that produce Gerstner waves, neither has it been proven that such solutions do not exist. At the same time, we are unaware of any explanation based on Stokes wave theory that can describe Smith’s observations that mean Eulerian flows developed that cancelled the Stokes drift associated with passing wave groups.
An important aspect of Pollard’s solution is that it does not include the effects of mean currents. In the present paper we extend Pollard’s solution to include a depth-invariant mean current. The dispersion relation for the wave motions in this case is defined by a sixth-order polynomial that we find has 4 real roots. The two larger of these roots describe the waves that Pollard found, i.e. Gerstner waves as slightly altered by rotation, whereas the two small roots define a new type of wave that decays strongly with depth from the free surface such that very long wavelength motions still satisfy the requirements of the Lagrangian deep water-wave analysis, i.e. that the motions are not influenced by the presence of the bottom of the ocean.
2 The governing equations
We investigate surface water waves propagating zonally in a relatively narrow ocean strip less than a few degrees of latitude wide and so we regard the Coriolis parameters
as constant. Here
![]() $\unicode[STIX]{x1D719}$
denotes the latitude and
$\unicode[STIX]{x1D719}$
denotes the latitude and
![]() $\unicode[STIX]{x1D6FA}=7.29\times \,10^{-5}~\text{rad}~\text{s}^{-1}$
is the rate of rotation of the Earth. For example, the values
$\unicode[STIX]{x1D6FA}=7.29\times \,10^{-5}~\text{rad}~\text{s}^{-1}$
is the rate of rotation of the Earth. For example, the values
![]() $f=\hat{f}=10^{-4}~\text{s}^{-1}$
are appropriate to
$f=\hat{f}=10^{-4}~\text{s}^{-1}$
are appropriate to
![]() $45^{\circ }$
latitude in the Northern hemisphere; see Gill (Reference Gill1982). In terms of the Cartesian coordinate system with the zonal coordinate
$45^{\circ }$
latitude in the Northern hemisphere; see Gill (Reference Gill1982). In terms of the Cartesian coordinate system with the zonal coordinate
![]() $x$
pointing east, the meridional coordinate
$x$
pointing east, the meridional coordinate
![]() $y$
pointing north and the vertical coordinate
$y$
pointing north and the vertical coordinate
![]() $z$
pointing up, the governing equations in the
$z$
pointing up, the governing equations in the
![]() $f$
-plane approximation we solve are the Euler equations
$f$
-plane approximation we solve are the Euler equations
 $$\begin{eqnarray}\left.\begin{array}{@{}l@{}}u_{t}+uu_{x}+vu_{y}+wu_{z}+\hat{f}\,w-f\,v=-\,\displaystyle \frac{1}{\unicode[STIX]{x1D70C}}\,P_{x},\\ v_{t}+uv_{x}+vv_{y}+wv_{z}+f\,u=-\,\displaystyle \frac{1}{\unicode[STIX]{x1D70C}}\,P_{y},\\ w_{t}+uw_{x}+vw_{y}+ww_{z}-\hat{f}\,u=-\,\displaystyle \frac{1}{\unicode[STIX]{x1D70C}}\,P_{z}-g,\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}l@{}}u_{t}+uu_{x}+vu_{y}+wu_{z}+\hat{f}\,w-f\,v=-\,\displaystyle \frac{1}{\unicode[STIX]{x1D70C}}\,P_{x},\\ v_{t}+uv_{x}+vv_{y}+wv_{z}+f\,u=-\,\displaystyle \frac{1}{\unicode[STIX]{x1D70C}}\,P_{y},\\ w_{t}+uw_{x}+vw_{y}+ww_{z}-\hat{f}\,u=-\,\displaystyle \frac{1}{\unicode[STIX]{x1D70C}}\,P_{z}-g,\end{array}\right\}\end{eqnarray}$$
coupled with the equation of mass conservation
and with the condition of incompressibility
Here
![]() $t$
is time,
$t$
is time,
![]() $(u,\,v,\,w)$
is the fluid velocity,
$(u,\,v,\,w)$
is the fluid velocity,
![]() $P$
is the pressure,
$P$
is the pressure,
![]() $g=9.8~\text{ms}^{-2}$
is the (constant) gravitational acceleration at the Earth’s surface and
$g=9.8~\text{ms}^{-2}$
is the (constant) gravitational acceleration at the Earth’s surface and
![]() $\unicode[STIX]{x1D70C}$
is the water’s density. The appropriate boundary conditions for deep water waves are the dynamic boundary condition
$\unicode[STIX]{x1D70C}$
is the water’s density. The appropriate boundary conditions for deep water waves are the dynamic boundary condition
where
![]() $P_{atm}$
is the constant pressure of the atmosphere at the surface of the ocean, and
$P_{atm}$
is the constant pressure of the atmosphere at the surface of the ocean, and
together with the requirement that the wave motion is insignificant at great depths.
For our purposes it is convenient to use the Lagrangian framework. We will show that an explicit solution to the governing equations (2.2)–(2.6), with a depth-invariant mean current, is provided by specifying, at time
![]() $t$
, the positions
$t$
, the positions
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}x=q-c_{0}\,t-b\,\text{e}^{ms}\sin [k(q-ct)],\\ y=r-d\,\text{e}^{ms}\cos [k(q-ct)],\\ z=s+a\,\text{e}^{ms}\cos [k(q-ct)],\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}x=q-c_{0}\,t-b\,\text{e}^{ms}\sin [k(q-ct)],\\ y=r-d\,\text{e}^{ms}\cos [k(q-ct)],\\ z=s+a\,\text{e}^{ms}\cos [k(q-ct)],\end{array}\right\}\end{eqnarray}$$
of the fluid particles in terms of the labelling variables
![]() $(q,r,s)$
and the real parameters
$(q,r,s)$
and the real parameters
![]() $a$
,
$a$
,
![]() $b$
,
$b$
,
![]() $c$
,
$c$
,
![]() $d$
,
$d$
,
![]() $k$
,
$k$
,
![]() $m$
. Here
$m$
. Here
![]() $c_{0}$
is the current velocity,
$c_{0}$
is the current velocity,
![]() $k=2\unicode[STIX]{x03C0}/L$
is the wavenumber corresponding to the wavelength
$k=2\unicode[STIX]{x03C0}/L$
is the wavenumber corresponding to the wavelength
![]() $L$
,
$L$
,
![]() $c$
is the wave speed, and
$c$
is the wave speed, and
![]() $b$
,
$b$
,
![]() $d$
and
$d$
and
![]() $c$
are suitably chosen in terms of
$c$
are suitably chosen in terms of
![]() $k>0$
,
$k>0$
,
![]() $m>0$
and
$m>0$
and
![]() $a>0$
; we shall see, cf. (2.30) below, that
$a>0$
; we shall see, cf. (2.30) below, that
![]() $b>0$
while the sign of
$b>0$
while the sign of
![]() $d$
varies (
$d$
varies (
![]() $d>0$
in the Southern hemisphere,
$d>0$
in the Southern hemisphere,
![]() $d<0$
in the Northern hemisphere and
$d<0$
in the Northern hemisphere and
![]() $d=0$
on the Equator). Anticipating the relation
$d=0$
on the Equator). Anticipating the relation
![]() $b^{2}=a^{2}+d^{2}$
, cf. (2.28) below, we note that (2.7) represents a wave with crests parallel to the
$b^{2}=a^{2}+d^{2}$
, cf. (2.28) below, we note that (2.7) represents a wave with crests parallel to the
![]() $y$
-axis, propagating in a West–East direction (see figure 1), with the particles moving in trochoidal orbits – curves described by a fixed point on a circle of radius
$y$
-axis, propagating in a West–East direction (see figure 1), with the particles moving in trochoidal orbits – curves described by a fixed point on a circle of radius
![]() $b\,\text{e}^{ms}$
, with a centre at
$b\,\text{e}^{ms}$
, with a centre at
![]() $(q-c_{0}t,\,r,\,s)$
, rolling at constant speed
$(q-c_{0}t,\,r,\,s)$
, rolling at constant speed
![]() $c_{0}$
eastward along the
$c_{0}$
eastward along the
![]() $x$
-axis, in a plane that is at an angle
$x$
-axis, in a plane that is at an angle
![]() $\arctan (d/a)$
to the vertical (see figure 2). Note that a circle in three dimensions is parametrized by six numbers (two for the orientation of the unit vector
$\arctan (d/a)$
to the vertical (see figure 2). Note that a circle in three dimensions is parametrized by six numbers (two for the orientation of the unit vector
![]() $\unicode[STIX]{x1D742}$
which is normal to the plane of the circle, one for the radius
$\unicode[STIX]{x1D742}$
which is normal to the plane of the circle, one for the radius
![]() $\unicode[STIX]{x1D6FF}$
of the circle and three for the circle’s centre
$\unicode[STIX]{x1D6FF}$
of the circle and three for the circle’s centre
![]() $\boldsymbol{C}$
):
$\boldsymbol{C}$
):
where
![]() $\unicode[STIX]{x1D741}$
is a unit vector orthogonal to
$\unicode[STIX]{x1D741}$
is a unit vector orthogonal to
![]() $\unicode[STIX]{x1D742}$
and
$\unicode[STIX]{x1D742}$
and
![]() $\unicode[STIX]{x1D703}$
is the angular position on the circle; we recover (2.7) with
$\unicode[STIX]{x1D703}$
is the angular position on the circle; we recover (2.7) with
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\boldsymbol{C}=(q-c_{0}t,\,r,\,s),\quad \unicode[STIX]{x1D741}=\left(0,\,-{\displaystyle \frac{d}{b}},{\displaystyle \frac{a}{b}}\right),\quad \unicode[STIX]{x1D742}=-\left(0,\,{\displaystyle \frac{a}{b}},{\displaystyle \frac{d}{b}}\right),\\ \unicode[STIX]{x1D703}=[k(q-ct)],\quad \unicode[STIX]{x1D6FF}=b\,\text{e}^{ms}.\end{array}\right\}.\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\boldsymbol{C}=(q-c_{0}t,\,r,\,s),\quad \unicode[STIX]{x1D741}=\left(0,\,-{\displaystyle \frac{d}{b}},{\displaystyle \frac{a}{b}}\right),\quad \unicode[STIX]{x1D742}=-\left(0,\,{\displaystyle \frac{a}{b}},{\displaystyle \frac{d}{b}}\right),\\ \unicode[STIX]{x1D703}=[k(q-ct)],\quad \unicode[STIX]{x1D6FF}=b\,\text{e}^{ms}.\end{array}\right\}.\end{eqnarray}$$
Since
![]() $a>0$
,
$a>0$
,
![]() $b>0$
and the sign of
$b>0$
and the sign of
![]() $d$
changes across the Equator, an examination of the components of the vector
$d$
changes across the Equator, an examination of the components of the vector
![]() $\unicode[STIX]{x1D741}$
shows that only the equatorial waves (for which
$\unicode[STIX]{x1D741}$
shows that only the equatorial waves (for which
![]() $d=0$
) are symmetric with respect to the local vertical in the meridional direction, all other waves being tilted towards the pole in their hemisphere with an angle of inclination from the vertical that increases with latitude. Let us also point out that the above considerations show that the labelling variables do not represent the initial position of the particle they define. In (2.7), the labelling variable
$d=0$
) are symmetric with respect to the local vertical in the meridional direction, all other waves being tilted towards the pole in their hemisphere with an angle of inclination from the vertical that increases with latitude. Let us also point out that the above considerations show that the labelling variables do not represent the initial position of the particle they define. In (2.7), the labelling variable
![]() $q$
runs over the entire line, while
$q$
runs over the entire line, while
![]() $r$
covers an interval
$r$
covers an interval
![]() $(-r_{0},\,r_{0})$
for some
$(-r_{0},\,r_{0})$
for some
![]() $r_{0}$
, and at every fixed value of
$r_{0}$
, and at every fixed value of
![]() $r$
we allow
$r$
we allow
![]() $s\leqslant s_{0}(r)$
for some value
$s\leqslant s_{0}(r)$
for some value
![]() $s_{0}(r)<0$
that corresponds to the free surface, to be determined later on: at the fixed latitude
$s_{0}(r)<0$
that corresponds to the free surface, to be determined later on: at the fixed latitude
![]() $r$
, setting
$r$
, setting
![]() $s=s_{0}(r)$
in (2.7) provides us with a parametrization of the surface wave at time
$s=s_{0}(r)$
in (2.7) provides us with a parametrization of the surface wave at time
![]() $t$
as
$t$
as
![]() $q$
varies. Beneath the surface waves, the constraint
$q$
varies. Beneath the surface waves, the constraint
![]() $m>0$
forces the amplitude of the vertical oscillations of a particle to decay exponentially with increasing depth. With
$m>0$
forces the amplitude of the vertical oscillations of a particle to decay exponentially with increasing depth. With
![]() $c_{0}$
interpreted as the mean flow velocity, the wave–current interaction specified by (2.7) therefore presents a negligible wave component at large depths – in such regions the flow is merely a pure horizontal current.
$c_{0}$
interpreted as the mean flow velocity, the wave–current interaction specified by (2.7) therefore presents a negligible wave component at large depths – in such regions the flow is merely a pure horizontal current.

Figure 1. While the equatorial waves are symmetric with respect to the local vertical, all other waves are slightly tilted towards the pole in their hemisphere. There is no change in the
![]() $y$
-direction but in some regimes the wave has pronounced flat troughs and sharp crests: for
$y$
-direction but in some regimes the wave has pronounced flat troughs and sharp crests: for
![]() $\unicode[STIX]{x1D719}=60\,^{\circ }\text{S}$
, note the trochoidal shape of the wave with
$\unicode[STIX]{x1D719}=60\,^{\circ }\text{S}$
, note the trochoidal shape of the wave with
![]() $c_{0}=0.3~\text{m}~\text{s}^{-1}$
,
$c_{0}=0.3~\text{m}~\text{s}^{-1}$
,
![]() $k=6.28\times 10^{-2}~\text{m}^{-1}$
,
$k=6.28\times 10^{-2}~\text{m}^{-1}$
,
![]() $a=10$
m, seen in (a), versus the sinusoidal shape for the smaller amplitude (and much longer) wave with
$a=10$
m, seen in (a), versus the sinusoidal shape for the smaller amplitude (and much longer) wave with
![]() $c_{0}=0.3~\text{m}~\text{s}^{-1}$
,
$c_{0}=0.3~\text{m}~\text{s}^{-1}$
,
![]() $k=6.28\times 10^{-2}~\text{m}^{-1}$
,
$k=6.28\times 10^{-2}~\text{m}^{-1}$
,
![]() $a=2~\text{cm}$
,seen in (b).
$a=2~\text{cm}$
,seen in (b).

Figure 2. Wave-induced particle motions on the water surface for
![]() $a=2~\text{cm}$
,
$a=2~\text{cm}$
,
![]() $c_{0}=0.3~\text{m}~\text{s}^{-1}$
,
$c_{0}=0.3~\text{m}~\text{s}^{-1}$
,
![]() $k=6.28\times 10^{-7}~\text{m}^{-1}$
and
$k=6.28\times 10^{-7}~\text{m}^{-1}$
and
![]() $\unicode[STIX]{x1D719}=60\,^{\circ }\text{S}$
: (a) trajectory as seen in a fixed coordinate system; and (b) trajectory as seen in a coordinate system moving with the mean flow, where the closed orbit that typifies Gerstner waves is readily apparent.
$\unicode[STIX]{x1D719}=60\,^{\circ }\text{S}$
: (a) trajectory as seen in a fixed coordinate system; and (b) trajectory as seen in a coordinate system moving with the mean flow, where the closed orbit that typifies Gerstner waves is readily apparent.
Assuming constant density
![]() $\unicode[STIX]{x1D70C}_{0}$
throughout the fluid, let us find the relations between the various parameters in (2.7) required for it to represent an exact solution. Set
$\unicode[STIX]{x1D70C}_{0}$
throughout the fluid, let us find the relations between the various parameters in (2.7) required for it to represent an exact solution. Set
The Jacobian of the map relating the particle positions to the Lagrangian labelling variables is obtained by computing the determinant
![]() $D$
of the matrix
$D$
of the matrix
 $$\begin{eqnarray}\left(\begin{array}{@{}ccc@{}}\displaystyle \frac{\unicode[STIX]{x2202}x}{\unicode[STIX]{x2202}q} & \displaystyle \frac{\unicode[STIX]{x2202}y}{\unicode[STIX]{x2202}q} & \displaystyle \frac{\unicode[STIX]{x2202}z}{\unicode[STIX]{x2202}q}\\ \displaystyle \frac{\unicode[STIX]{x2202}x}{\unicode[STIX]{x2202}r} & \displaystyle \frac{\unicode[STIX]{x2202}y}{\unicode[STIX]{x2202}r} & \displaystyle \frac{\unicode[STIX]{x2202}z}{\unicode[STIX]{x2202}r}\\ \displaystyle \frac{\unicode[STIX]{x2202}x}{\unicode[STIX]{x2202}s} & \displaystyle \frac{\unicode[STIX]{x2202}y}{\unicode[STIX]{x2202}s} & \displaystyle \frac{\unicode[STIX]{x2202}z}{\unicode[STIX]{x2202}s}\end{array}\right)=\left(\begin{array}{@{}ccc@{}}1-bk\,\text{e}^{\unicode[STIX]{x1D709}}\cos \unicode[STIX]{x1D703} & dk\,\text{e}^{\unicode[STIX]{x1D709}}\sin \unicode[STIX]{x1D703} & -ak\,\text{e}^{\unicode[STIX]{x1D709}}\sin \unicode[STIX]{x1D703}\\ 0 & 1 & 0\\ -bm\,\text{e}^{\unicode[STIX]{x1D709}}\sin \unicode[STIX]{x1D703} & -dm\,\text{e}^{\unicode[STIX]{x1D709}}\cos \unicode[STIX]{x1D703} & 1+am\,\text{e}^{\unicode[STIX]{x1D709}}\cos \unicode[STIX]{x1D703}\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}ccc@{}}\displaystyle \frac{\unicode[STIX]{x2202}x}{\unicode[STIX]{x2202}q} & \displaystyle \frac{\unicode[STIX]{x2202}y}{\unicode[STIX]{x2202}q} & \displaystyle \frac{\unicode[STIX]{x2202}z}{\unicode[STIX]{x2202}q}\\ \displaystyle \frac{\unicode[STIX]{x2202}x}{\unicode[STIX]{x2202}r} & \displaystyle \frac{\unicode[STIX]{x2202}y}{\unicode[STIX]{x2202}r} & \displaystyle \frac{\unicode[STIX]{x2202}z}{\unicode[STIX]{x2202}r}\\ \displaystyle \frac{\unicode[STIX]{x2202}x}{\unicode[STIX]{x2202}s} & \displaystyle \frac{\unicode[STIX]{x2202}y}{\unicode[STIX]{x2202}s} & \displaystyle \frac{\unicode[STIX]{x2202}z}{\unicode[STIX]{x2202}s}\end{array}\right)=\left(\begin{array}{@{}ccc@{}}1-bk\,\text{e}^{\unicode[STIX]{x1D709}}\cos \unicode[STIX]{x1D703} & dk\,\text{e}^{\unicode[STIX]{x1D709}}\sin \unicode[STIX]{x1D703} & -ak\,\text{e}^{\unicode[STIX]{x1D709}}\sin \unicode[STIX]{x1D703}\\ 0 & 1 & 0\\ -bm\,\text{e}^{\unicode[STIX]{x1D709}}\sin \unicode[STIX]{x1D703} & -dm\,\text{e}^{\unicode[STIX]{x1D709}}\cos \unicode[STIX]{x1D703} & 1+am\,\text{e}^{\unicode[STIX]{x1D709}}\cos \unicode[STIX]{x1D703}\end{array}\right).\end{eqnarray}$$
The flow is volume-preserving if and only if this determinant is time independent. Since
![]() $D=(am-bk)\,\text{e}^{\unicode[STIX]{x1D709}}\cos \unicode[STIX]{x1D703}+1-abmk\,\text{e}^{2\unicode[STIX]{x1D709}}$
, this yields the relation
$D=(am-bk)\,\text{e}^{\unicode[STIX]{x1D709}}\cos \unicode[STIX]{x1D703}+1-abmk\,\text{e}^{2\unicode[STIX]{x1D709}}$
, this yields the relation
Furthermore, in addition to (2.12), we also have to impose the constraint
in order to ensure, by means of the inverse function theorem, that the labelling (2.7) represents a valid local diffeomorphic change of coordinates. Due to (2.12) and the fact that we allow all values
![]() $\unicode[STIX]{x1D709}\leqslant s_{0}(r)<0$
, (2.13) is equivalent to
$\unicode[STIX]{x1D709}\leqslant s_{0}(r)<0$
, (2.13) is equivalent to
A glance at (2.7) confirms that
![]() $a\text{e}^{ms_{0}(r)}$
is the surface wave amplitude at latitude
$a\text{e}^{ms_{0}(r)}$
is the surface wave amplitude at latitude
![]() $r$
, so that (2.14) expresses the fact that
$r$
, so that (2.14) expresses the fact that
![]() $1/m$
is an upper bound for the wave amplitude.
$1/m$
is an upper bound for the wave amplitude.
Let us now write the Euler equation (2.2) in the form
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \frac{\text{D}u}{\text{D}t}+\hat{f}\,w-f\,v=-\,\frac{1}{\unicode[STIX]{x1D70C}_{0}}\,P_{x},\\ \displaystyle \frac{\text{D}v}{\text{D}t}+f\,u=-\,\frac{1}{\unicode[STIX]{x1D70C}_{0}}\,P_{y},\\ \displaystyle \frac{\text{D}w}{\text{D}t}-\hat{f}\,u=-\,\frac{1}{\unicode[STIX]{x1D70C}_{0}}\,P_{z}-g,\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \frac{\text{D}u}{\text{D}t}+\hat{f}\,w-f\,v=-\,\frac{1}{\unicode[STIX]{x1D70C}_{0}}\,P_{x},\\ \displaystyle \frac{\text{D}v}{\text{D}t}+f\,u=-\,\frac{1}{\unicode[STIX]{x1D70C}_{0}}\,P_{y},\\ \displaystyle \frac{\text{D}w}{\text{D}t}-\hat{f}\,u=-\,\frac{1}{\unicode[STIX]{x1D70C}_{0}}\,P_{z}-g,\end{array}\right\}\end{eqnarray}$$
where
![]() $\text{D}/\text{D}t$
stands for the material derivative. From (2.7) we can compute the velocity and acceleration of a particle as
$\text{D}/\text{D}t$
stands for the material derivative. From (2.7) we can compute the velocity and acceleration of a particle as
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}u=\displaystyle \frac{\text{D}x}{\text{D}t}=-c_{0}+bkc\,\text{e}^{\unicode[STIX]{x1D709}}\cos \unicode[STIX]{x1D703},\\ v=\displaystyle \frac{\text{D}y}{\text{D}t}=-dk\,c\,\text{e}^{\unicode[STIX]{x1D709}}\sin \unicode[STIX]{x1D703},\\ w=\displaystyle \frac{\text{D}z}{\text{D}t}=akc\,\text{e}^{\unicode[STIX]{x1D709}}\sin \unicode[STIX]{x1D703},\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}u=\displaystyle \frac{\text{D}x}{\text{D}t}=-c_{0}+bkc\,\text{e}^{\unicode[STIX]{x1D709}}\cos \unicode[STIX]{x1D703},\\ v=\displaystyle \frac{\text{D}y}{\text{D}t}=-dk\,c\,\text{e}^{\unicode[STIX]{x1D709}}\sin \unicode[STIX]{x1D703},\\ w=\displaystyle \frac{\text{D}z}{\text{D}t}=akc\,\text{e}^{\unicode[STIX]{x1D709}}\sin \unicode[STIX]{x1D703},\end{array}\right\}\end{eqnarray}$$
and
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \frac{\text{D}u}{\text{D}t}=bk^{2}c^{2}\,\text{e}^{\unicode[STIX]{x1D709}}\sin \unicode[STIX]{x1D703},\\ \displaystyle \frac{\text{D}v}{\text{D}t}=dk^{2}c^{2}\,\text{e}^{\unicode[STIX]{x1D709}}\cos \unicode[STIX]{x1D703},\\ \displaystyle \frac{\text{D}w}{\text{D}t}=-ak^{2}c^{2}\,\text{e}^{\unicode[STIX]{x1D709}}\cos \unicode[STIX]{x1D703},\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \frac{\text{D}u}{\text{D}t}=bk^{2}c^{2}\,\text{e}^{\unicode[STIX]{x1D709}}\sin \unicode[STIX]{x1D703},\\ \displaystyle \frac{\text{D}v}{\text{D}t}=dk^{2}c^{2}\,\text{e}^{\unicode[STIX]{x1D709}}\cos \unicode[STIX]{x1D703},\\ \displaystyle \frac{\text{D}w}{\text{D}t}=-ak^{2}c^{2}\,\text{e}^{\unicode[STIX]{x1D709}}\cos \unicode[STIX]{x1D703},\end{array}\right\}\end{eqnarray}$$
respectively. We can therefore write (2.15) as
The change of variables
 $$\begin{eqnarray}\left(\begin{array}{@{}c@{}}P_{q}\\ P_{r}\\ P_{s}\end{array}\right)=\left(\begin{array}{@{}ccc@{}}\displaystyle \frac{\unicode[STIX]{x2202}x}{\unicode[STIX]{x2202}q} & \displaystyle \frac{\unicode[STIX]{x2202}y}{\unicode[STIX]{x2202}q} & \displaystyle \frac{\unicode[STIX]{x2202}z}{\unicode[STIX]{x2202}q}\\ \displaystyle \frac{\unicode[STIX]{x2202}x}{\unicode[STIX]{x2202}r} & \displaystyle \frac{\unicode[STIX]{x2202}y}{\unicode[STIX]{x2202}r} & \displaystyle \frac{\unicode[STIX]{x2202}z}{\unicode[STIX]{x2202}r}\\ \displaystyle \frac{\unicode[STIX]{x2202}x}{\unicode[STIX]{x2202}s} & \displaystyle \frac{\unicode[STIX]{x2202}y}{\unicode[STIX]{x2202}s} & \displaystyle \frac{\unicode[STIX]{x2202}z}{\unicode[STIX]{x2202}s}\end{array}\right)\,\left(\begin{array}{@{}c@{}}P_{x}\\ P_{y}\\ P_{z}\end{array}\right)\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}c@{}}P_{q}\\ P_{r}\\ P_{s}\end{array}\right)=\left(\begin{array}{@{}ccc@{}}\displaystyle \frac{\unicode[STIX]{x2202}x}{\unicode[STIX]{x2202}q} & \displaystyle \frac{\unicode[STIX]{x2202}y}{\unicode[STIX]{x2202}q} & \displaystyle \frac{\unicode[STIX]{x2202}z}{\unicode[STIX]{x2202}q}\\ \displaystyle \frac{\unicode[STIX]{x2202}x}{\unicode[STIX]{x2202}r} & \displaystyle \frac{\unicode[STIX]{x2202}y}{\unicode[STIX]{x2202}r} & \displaystyle \frac{\unicode[STIX]{x2202}z}{\unicode[STIX]{x2202}r}\\ \displaystyle \frac{\unicode[STIX]{x2202}x}{\unicode[STIX]{x2202}s} & \displaystyle \frac{\unicode[STIX]{x2202}y}{\unicode[STIX]{x2202}s} & \displaystyle \frac{\unicode[STIX]{x2202}z}{\unicode[STIX]{x2202}s}\end{array}\right)\,\left(\begin{array}{@{}c@{}}P_{x}\\ P_{y}\\ P_{z}\end{array}\right)\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle P_{s} & = & \displaystyle \unicode[STIX]{x1D70C}_{0}\big\{-\hat{f}c_{0}\,-\,g+\hat{f}abckm\,\text{e}^{2\unicode[STIX]{x1D709}}+\,fbdc\,km\,\text{e}^{2\unicode[STIX]{x1D709}}+mb^{2}k^{2}c^{2}\,\text{e}^{2\unicode[STIX]{x1D709}}\nonumber\\ \displaystyle & & \displaystyle +\,(ak^{2}c^{2}+\hat{f}bkc-agm-f\,\text{d}m\,c_{0}-\hat{f}c_{0}am)\,\text{e}^{\unicode[STIX]{x1D709}}\,\cos \unicode[STIX]{x1D703}\nonumber\\ \displaystyle & & \displaystyle +\,mk^{2}c^{2}\,(d^{2}+a^{2}-b^{2})\,\text{e}^{2\unicode[STIX]{x1D709}}\,\cos ^{2}\unicode[STIX]{x1D703}\big\}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle P_{s} & = & \displaystyle \unicode[STIX]{x1D70C}_{0}\big\{-\hat{f}c_{0}\,-\,g+\hat{f}abckm\,\text{e}^{2\unicode[STIX]{x1D709}}+\,fbdc\,km\,\text{e}^{2\unicode[STIX]{x1D709}}+mb^{2}k^{2}c^{2}\,\text{e}^{2\unicode[STIX]{x1D709}}\nonumber\\ \displaystyle & & \displaystyle +\,(ak^{2}c^{2}+\hat{f}bkc-agm-f\,\text{d}m\,c_{0}-\hat{f}c_{0}am)\,\text{e}^{\unicode[STIX]{x1D709}}\,\cos \unicode[STIX]{x1D703}\nonumber\\ \displaystyle & & \displaystyle +\,mk^{2}c^{2}\,(d^{2}+a^{2}-b^{2})\,\text{e}^{2\unicode[STIX]{x1D709}}\,\cos ^{2}\unicode[STIX]{x1D703}\big\}.\end{eqnarray}$$
The equality of the mixed partial derivatives of
![]() $P$
with respect to the labelling variables
$P$
with respect to the labelling variables
![]() $(q,\,r,\,s)$
leads to relations
$(q,\,r,\,s)$
leads to relations
and
if we take (2.12) into account. With the constraints (2.25)–(2.26) in place, note that, for every constant
![]() $P_{0}$
, the gradient of the expression
$P_{0}$
, the gradient of the expression
 $$\begin{eqnarray}\displaystyle P(q-ct,r,s) & = & \displaystyle P_{0}+\unicode[STIX]{x1D70C}_{0}fc_{0}\,r-\unicode[STIX]{x1D70C}_{0}(g+\hat{f}c_{0})\,s\,\nonumber\\ \displaystyle & & \displaystyle +\,{\textstyle \frac{1}{2}}\,\unicode[STIX]{x1D70C}_{0}\,\hat{f}abck\,\text{e}^{2\unicode[STIX]{x1D709}}+{\textstyle \frac{1}{2}}\,\unicode[STIX]{x1D70C}_{0}\,fbdck\,\text{e}^{2\unicode[STIX]{x1D709}}+{\textstyle \frac{1}{2}}\,\unicode[STIX]{x1D70C}_{0}\,b^{2}k^{2}c^{2}\,\text{e}^{2\unicode[STIX]{x1D709}}\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D70C}_{0}\,(bkc^{2}+\hat{f}ac+fdc-ag-fdc_{0}-\hat{f}c_{0}a)\,\text{e}^{\unicode[STIX]{x1D709}}\,\cos \unicode[STIX]{x1D703}\nonumber\\ \displaystyle & & \displaystyle +\,{\textstyle \frac{1}{2}}\,\unicode[STIX]{x1D70C}_{0}\,k^{2}c^{2}\,(d^{2}+a^{2}-b^{2})\,\text{e}^{2\unicode[STIX]{x1D709}}\,\cos ^{2}\unicode[STIX]{x1D703},\quad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle P(q-ct,r,s) & = & \displaystyle P_{0}+\unicode[STIX]{x1D70C}_{0}fc_{0}\,r-\unicode[STIX]{x1D70C}_{0}(g+\hat{f}c_{0})\,s\,\nonumber\\ \displaystyle & & \displaystyle +\,{\textstyle \frac{1}{2}}\,\unicode[STIX]{x1D70C}_{0}\,\hat{f}abck\,\text{e}^{2\unicode[STIX]{x1D709}}+{\textstyle \frac{1}{2}}\,\unicode[STIX]{x1D70C}_{0}\,fbdck\,\text{e}^{2\unicode[STIX]{x1D709}}+{\textstyle \frac{1}{2}}\,\unicode[STIX]{x1D70C}_{0}\,b^{2}k^{2}c^{2}\,\text{e}^{2\unicode[STIX]{x1D709}}\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D70C}_{0}\,(bkc^{2}+\hat{f}ac+fdc-ag-fdc_{0}-\hat{f}c_{0}a)\,\text{e}^{\unicode[STIX]{x1D709}}\,\cos \unicode[STIX]{x1D703}\nonumber\\ \displaystyle & & \displaystyle +\,{\textstyle \frac{1}{2}}\,\unicode[STIX]{x1D70C}_{0}\,k^{2}c^{2}\,(d^{2}+a^{2}-b^{2})\,\text{e}^{2\unicode[STIX]{x1D709}}\,\cos ^{2}\unicode[STIX]{x1D703},\quad\end{eqnarray}$$
with respect to the labelling variables is given by the right-hand side of (2.22)–(2.24). Therefore the free surface is identified at the meridional distance
![]() $r$
from the reference latitude by specifying a value
$r$
from the reference latitude by specifying a value
![]() $s_{0}(r)$
of the label
$s_{0}(r)$
of the label
![]() $s$
for which the expression in (2.27) equals to
$s$
for which the expression in (2.27) equals to
![]() $P_{atm}$
, thus validating (2.5) and (2.6). This is possible if and only if the right-hand side of the expression (2.27) is time independent, in which case the value of
$P_{atm}$
, thus validating (2.5) and (2.6). This is possible if and only if the right-hand side of the expression (2.27) is time independent, in which case the value of
![]() $s_{0}(r)$
is found by solving the implicit functional equation
$s_{0}(r)$
is found by solving the implicit functional equation
![]() $P=P_{atm}$
for a fixed value of
$P=P_{atm}$
for a fixed value of
![]() $r$
. The time independence of the expression (2.27) holds if
$r$
. The time independence of the expression (2.27) holds if
and
From (2.12) and (2.25) we obtain
so that for
![]() $a\neq 0$
we can recast both (2.26) and (2.28) as
$a\neq 0$
we can recast both (2.26) and (2.28) as
The remaining relation between the parameters, (2.29), takes on the form
Squaring (2.32), we can take advantage of (2.31) to obtain the dispersion relation
The non-zero roots of (2.33) are theoretically admissible wave propagation speeds if
![]() $c_{0}\neq 0$
. However, if
$c_{0}\neq 0$
. However, if
![]() $c_{0}=0$
, then the physically relevant roots of (2.33) are those that differ from
$c_{0}=0$
, then the physically relevant roots of (2.33) are those that differ from
![]() $c=\pm f/k$
; thus, the latter are extraneous roots, ruled out by (2.31).
$c=\pm f/k$
; thus, the latter are extraneous roots, ruled out by (2.31).
For equatorial waves we have
![]() $f=0$
and
$f=0$
and
![]() $\hat{f}=2\unicode[STIX]{x1D6FA}$
, so that (2.33) reduces to
$\hat{f}=2\unicode[STIX]{x1D6FA}$
, so that (2.33) reduces to
yielding
In the absence of an underlying current (for
![]() $c_{0}=0$
) we recover a result of Hsu (Reference Hsu2015). On the other hand, at mid-latitudes we have
$c_{0}=0$
) we recover a result of Hsu (Reference Hsu2015). On the other hand, at mid-latitudes we have
![]() $f\neq 0$
and it is convenient to write the dispersion relation (2.33) as
$f\neq 0$
and it is convenient to write the dispersion relation (2.33) as
in terms of the non-dimensional variables
We can consider the extent to which surface wind waves might be affected by rotation by noting that their wavelengths typically range from 16 m to 400 m, so that
![]() $\sqrt{k/g}$
ranges from
$\sqrt{k/g}$
ranges from
![]() $0.2$
to
$0.2$
to
![]() $0.04~\text{s}~\text{m}^{-1}$
, while
$0.04~\text{s}~\text{m}^{-1}$
, while
![]() $\sqrt{gk}$
ranges from
$\sqrt{gk}$
ranges from
![]() $2~\text{s}^{-1}$
to
$2~\text{s}^{-1}$
to
![]() $0.4~\text{s}^{-1}$
. Note that
$0.4~\text{s}^{-1}$
. Note that
![]() $X=O(1)$
corresponds to a wind-wave speed
$X=O(1)$
corresponds to a wind-wave speed
![]() $c$
in the range from
$c$
in the range from
![]() $18~\text{km}~\text{h}^{-1}$
to
$18~\text{km}~\text{h}^{-1}$
to
![]() $80~\text{km}~\text{h}^{-1}$
. Given that
$80~\text{km}~\text{h}^{-1}$
. Given that
![]() $f$
is of the order of 10
$f$
is of the order of 10
![]() $^{-4}~\text{s}^{-1}$
, we see that
$^{-4}~\text{s}^{-1}$
, we see that
![]() $\unicode[STIX]{x1D700}=O(10^{-4})$
, and so, as concluded by Pollard (Reference Pollard1970), the effect of rotation is small. Typical currents do not exceed
$\unicode[STIX]{x1D700}=O(10^{-4})$
, and so, as concluded by Pollard (Reference Pollard1970), the effect of rotation is small. Typical currents do not exceed
![]() $1~\text{m}~\text{s}^{-1}$
, so that
$1~\text{m}~\text{s}^{-1}$
, so that
![]() $X_{0}=O(10^{-1})$
.
$X_{0}=O(10^{-1})$
.
The non-dimensional dispersion relation at mid-latitudes, (2.36), can be written out explicitly as a polynomial equation of degree six
![]() $P(X)=0$
, where
$P(X)=0$
, where
 $$\begin{eqnarray}\displaystyle P(X) & = & \displaystyle X^{6}-\unicode[STIX]{x1D700}^{2}(2+F^{2})\,X^{4}+2\unicode[STIX]{x1D700}\{F+\unicode[STIX]{x1D700}\,(1+F^{2})\,X_{0}\}\,X^{3}\nonumber\\ \displaystyle & & \displaystyle -\,\{1+2\unicode[STIX]{x1D700}F\,X_{0}+\unicode[STIX]{x1D700}^{2}F^{2}X_{0}^{2}\,-\,\unicode[STIX]{x1D700}^{4}(1+F^{2})\}\,X^{2}-\,2\unicode[STIX]{x1D700}^{3}\,\{F+\unicode[STIX]{x1D700}(1+F^{2})\,X_{0}\}\,X\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D700}^{2}\,\{1+2\unicode[STIX]{x1D700}F\,X_{0}+\unicode[STIX]{x1D700}^{2}(1+F^{2})X_{0}^{2}\}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle P(X) & = & \displaystyle X^{6}-\unicode[STIX]{x1D700}^{2}(2+F^{2})\,X^{4}+2\unicode[STIX]{x1D700}\{F+\unicode[STIX]{x1D700}\,(1+F^{2})\,X_{0}\}\,X^{3}\nonumber\\ \displaystyle & & \displaystyle -\,\{1+2\unicode[STIX]{x1D700}F\,X_{0}+\unicode[STIX]{x1D700}^{2}F^{2}X_{0}^{2}\,-\,\unicode[STIX]{x1D700}^{4}(1+F^{2})\}\,X^{2}-\,2\unicode[STIX]{x1D700}^{3}\,\{F+\unicode[STIX]{x1D700}(1+F^{2})\,X_{0}\}\,X\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D700}^{2}\,\{1+2\unicode[STIX]{x1D700}F\,X_{0}+\unicode[STIX]{x1D700}^{2}(1+F^{2})X_{0}^{2}\}.\end{eqnarray}$$
In linear wave propagation theory one can take advantage of the superposition principle by seeking a Fourier decomposition of an oscillatory wave motion in eigenmodes
![]() $\text{e}^{ik(q-ct)}$
, with the following interpretation for the disturbance from a state of equilibrium, at a fixed wavenumber
$\text{e}^{ik(q-ct)}$
, with the following interpretation for the disturbance from a state of equilibrium, at a fixed wavenumber
![]() $k>0$
:
$k>0$
:
-
(i) a real root
 $c$
of the dispersion relation generates two oscillatory eigenmodes of fixed amplitude,
$c$
of the dispersion relation generates two oscillatory eigenmodes of fixed amplitude,
 $\cos [k(q-ct)]$
and
$\cos [k(q-ct)]$
and
 $\sin [k(q-ct)]$
, which differ only by a phase;
$\sin [k(q-ct)]$
, which differ only by a phase; -
(ii) a complex root
 $c=\unicode[STIX]{x1D6FC}+i\unicode[STIX]{x1D6FD}$
, with
$c=\unicode[STIX]{x1D6FC}+i\unicode[STIX]{x1D6FD}$
, with
 $\unicode[STIX]{x1D6FC}\in \mathbb{R}$
and
$\unicode[STIX]{x1D6FC}\in \mathbb{R}$
and
 $\unicode[STIX]{x1D6FD}\in \mathbb{R}\setminus \{0\}$
, is indicative of evanescent or amplifying modes (according to whether
$\unicode[STIX]{x1D6FD}\in \mathbb{R}\setminus \{0\}$
, is indicative of evanescent or amplifying modes (according to whether
 $\unicode[STIX]{x1D6FD}>0$
or
$\unicode[STIX]{x1D6FD}>0$
or
 $\unicode[STIX]{x1D6FD}<0$
),
$\unicode[STIX]{x1D6FD}<0$
),
 $e^{-k\unicode[STIX]{x1D6FD}t}\cos [k(q-\unicode[STIX]{x1D6FC}t)]$
and
$e^{-k\unicode[STIX]{x1D6FD}t}\cos [k(q-\unicode[STIX]{x1D6FC}t)]$
and
 $\text{e}^{-k\unicode[STIX]{x1D6FD}t}\sin [k(q-\unicode[STIX]{x1D6FC}t)]$
, propagating at the speed
$\text{e}^{-k\unicode[STIX]{x1D6FD}t}\sin [k(q-\unicode[STIX]{x1D6FC}t)]$
, propagating at the speed
 $\unicode[STIX]{x1D6FC}$
with an amplitude that decays or is amplified in time by the exponential factor
$\unicode[STIX]{x1D6FC}$
with an amplitude that decays or is amplified in time by the exponential factor
 $k|\unicode[STIX]{x1D6FD}|$
.
$k|\unicode[STIX]{x1D6FD}|$
.
In contrast to this, (2.33) is the dispersion relation for the nonlinear wave–current interaction specified by the flow (2.7), and imaginary complex roots
![]() $c\in \mathbb{C}\setminus \mathbb{R}$
have to be discarded.
$c\in \mathbb{C}\setminus \mathbb{R}$
have to be discarded.
3 Solution of the dispersion relation and a description of the resulting wave motions
The exact roots of the polynomial
![]() $P(X)$
that defines the dispersion relation at mid-latitudes cannot be found analytically. An example plot of
$P(X)$
that defines the dispersion relation at mid-latitudes cannot be found analytically. An example plot of
![]() $P$
with parameters chosen to match the Antarctic circumpolar current (ACC), i.e. for 6
$P$
with parameters chosen to match the Antarctic circumpolar current (ACC), i.e. for 6
![]() $5\,^{\circ }\text{S}$
$5\,^{\circ }\text{S}$
![]() $f\approx -1.3\times 10^{-4}~\text{s}^{-1}$
and a mean current
$f\approx -1.3\times 10^{-4}~\text{s}^{-1}$
and a mean current
![]() $c_{0}=0.3~\text{m}~\text{s}^{-1}$
(see Constantin & Johnson (Reference Constantin and Johnson2016) for field data), is shown in figure 3 where two roots near
$c_{0}=0.3~\text{m}~\text{s}^{-1}$
(see Constantin & Johnson (Reference Constantin and Johnson2016) for field data), is shown in figure 3 where two roots near
![]() $\pm 1$
(figure 3
a) can be seen and two roots near
$\pm 1$
(figure 3
a) can be seen and two roots near
![]() $\pm \unicode[STIX]{x1D700}$
(figure 3
b) can also be seen. One can prove that the polynomial
$\pm \unicode[STIX]{x1D700}$
(figure 3
b) can also be seen. One can prove that the polynomial
![]() $P$
has exactly four real roots, two positive and two negative (see the discussion in the Appendix).
$P$
has exactly four real roots, two positive and two negative (see the discussion in the Appendix).

Figure 3. (a) Plot of the polynomial
![]() $P(X)$
showing the locations (circles) of the two
$P(X)$
showing the locations (circles) of the two
![]() $O(1)$
roots; (b) plot of
$O(1)$
roots; (b) plot of
![]() $P(X)$
showing the locations (circles) of the two
$P(X)$
showing the locations (circles) of the two
![]() $O(\unicode[STIX]{x1D700})$
roots. Coriolis and mean flow parameters are chosen to match the Antarctic circumpolar current (
$O(\unicode[STIX]{x1D700})$
roots. Coriolis and mean flow parameters are chosen to match the Antarctic circumpolar current (
![]() $f\approx -1.3\times 10^{-4}~\text{s}^{-1}$
and
$f\approx -1.3\times 10^{-4}~\text{s}^{-1}$
and
![]() $c_{0}=-0.3~\text{m}~\text{s}^{-1}$
).
$c_{0}=-0.3~\text{m}~\text{s}^{-1}$
).
Examination of figure 3 suggests that accurate analytical approximations of the roots to
![]() $P(X)$
can be found by a perturbation expansion in
$P(X)$
can be found by a perturbation expansion in
![]() $\unicode[STIX]{x1D700}$
:
$\unicode[STIX]{x1D700}$
:
After substitution into
![]() $P(X)$
and collecting different powers of
$P(X)$
and collecting different powers of
![]() $\unicode[STIX]{x1D700}$
, we find that at
$\unicode[STIX]{x1D700}$
, we find that at
![]() $O(1)$
$O(1)$
Thus
Note that the roots to the sixth-order polynomial that are near
![]() $\pm 1$
correspond to Gerstner waves that are very slightly modified by rotation, of the type found by Pollard (Reference Pollard1970). Since only real roots are relevant, in the rest of what follows we focus on the
$\pm 1$
correspond to Gerstner waves that are very slightly modified by rotation, of the type found by Pollard (Reference Pollard1970). Since only real roots are relevant, in the rest of what follows we focus on the
![]() $O(\unicode[STIX]{x1D700})$
roots. Assuming
$O(\unicode[STIX]{x1D700})$
roots. Assuming
![]() $x_{0}=0$
, then
$x_{0}=0$
, then
![]() $1-x_{1}^{2}=0$
at
$1-x_{1}^{2}=0$
at
![]() $O(\unicode[STIX]{x1D700})$
, which derives from the
$O(\unicode[STIX]{x1D700})$
, which derives from the
![]() $O(\unicode[STIX]{x1D700}^{2})$
expansion, so that
$O(\unicode[STIX]{x1D700}^{2})$
expansion, so that
Consideration of the
![]() $O(\unicode[STIX]{x1D700}^{3})$
terms shows that
$O(\unicode[STIX]{x1D700}^{3})$
terms shows that
![]() $x_{2}=0$
and finally, from the
$x_{2}=0$
and finally, from the
![]() $O(\unicode[STIX]{x1D700}^{4})$
terms, we find that
$O(\unicode[STIX]{x1D700}^{4})$
terms, we find that
![]() $X_{0}^{2}\mp 2x_{3}=0$
, that is,
$X_{0}^{2}\mp 2x_{3}=0$
, that is,
Thus an approximate solution to (3.1) shows two possible small roots that are approximately
Equation (3.6) implies that in dimensional terms, to
![]() $O(\unicode[STIX]{x1D700}^{2})$
,
$O(\unicode[STIX]{x1D700}^{2})$
,
For example for a 500 m long wave (
![]() $k\approx 1.3\times 10^{-2}~\text{m}^{-1}$
) on the ACC,
$k\approx 1.3\times 10^{-2}~\text{m}^{-1}$
) on the ACC,
![]() $c\approx 1~\text{cm}~\text{s}^{-1}$
since
$c\approx 1~\text{cm}~\text{s}^{-1}$
since
![]() $f\approx -1.25\times 10^{-4}~\text{s}^{-1}$
. On the other hand, for a
$f\approx -1.25\times 10^{-4}~\text{s}^{-1}$
. On the other hand, for a
![]() $10^{4}~\text{km}$
long wave (
$10^{4}~\text{km}$
long wave (
![]() $k\approx 6.2\times 10^{-7}~\text{m}^{-1}$
),
$k\approx 6.2\times 10^{-7}~\text{m}^{-1}$
),
![]() $c\approx 200~\text{m}~\text{s}^{-1}$
, comparable to typical open ocean barotropic long wave speeds. Note that the period
$c\approx 200~\text{m}~\text{s}^{-1}$
, comparable to typical open ocean barotropic long wave speeds. Note that the period
![]() $T$
for these waves is quite close to the inertial period since
$T$
for these waves is quite close to the inertial period since
 $$\begin{eqnarray}T\approx \displaystyle \frac{{\displaystyle \frac{2\unicode[STIX]{x03C0}}{k}}}{{\displaystyle \frac{f}{k}}}=\frac{2\unicode[STIX]{x03C0}}{f}=T_{i},\end{eqnarray}$$
$$\begin{eqnarray}T\approx \displaystyle \frac{{\displaystyle \frac{2\unicode[STIX]{x03C0}}{k}}}{{\displaystyle \frac{f}{k}}}=\frac{2\unicode[STIX]{x03C0}}{f}=T_{i},\end{eqnarray}$$
i.e. these slow waves are inertial waves, with inertial period
![]() $T_{i}$
.
$T_{i}$
.
The correction to
![]() $X$
at
$X$
at
![]() $O(\unicode[STIX]{x1D700}^{3})$
is important in light of (2.31), which can be written as
$O(\unicode[STIX]{x1D700}^{3})$
is important in light of (2.31), which can be written as
implying that
This gives a wavenumber that is much larger than
![]() $k$
since
$k$
since
![]() $g/(fc_{0})\gg 1$
. On the other hand, this also means that waves that are quite long with respect to the depth can produce surface-trapped motions that satisfy the fundamental assumption that the wave motions are not affected by the ocean’s bottom. For example, a wave with a wavelength of
$g/(fc_{0})\gg 1$
. On the other hand, this also means that waves that are quite long with respect to the depth can produce surface-trapped motions that satisfy the fundamental assumption that the wave motions are not affected by the ocean’s bottom. For example, a wave with a wavelength of
![]() $10^{4}~\text{km}$
(
$10^{4}~\text{km}$
(
![]() $k\approx 6.28\times 10^{-7}~\text{m}^{-1}$
) on a mean flow of
$k\approx 6.28\times 10^{-7}~\text{m}^{-1}$
) on a mean flow of
![]() $0.3~\text{m}~\text{s}^{-1}$
produces a vertical decay scale of approximately 6 m. We note that using satellite altimetry, White & Peterson (Reference White and Peterson1996) show evidence of waves in the ACC with wavelengths of approximately
$0.3~\text{m}~\text{s}^{-1}$
produces a vertical decay scale of approximately 6 m. We note that using satellite altimetry, White & Peterson (Reference White and Peterson1996) show evidence of waves in the ACC with wavelengths of approximately
![]() $11\times 10^{3}~\text{km}$
, and so it seems possible that waves can exist in the ACC that are sufficiently long to produce physically plausible decay scales according to our model. Moreover, consideration of the vertical scale also highlights the importance of the mean current in that if
$11\times 10^{3}~\text{km}$
, and so it seems possible that waves can exist in the ACC that are sufficiently long to produce physically plausible decay scales according to our model. Moreover, consideration of the vertical scale also highlights the importance of the mean current in that if
![]() $c_{0}=0$
, then (2.33) and (3.9) with
$c_{0}=0$
, then (2.33) and (3.9) with
![]() $c\approx \sqrt{g/k}$
yield
$c\approx \sqrt{g/k}$
yield
and so the corresponding decay scale is much smaller than in the presence of a mean current.
We now compute the amplitude
![]() $d$
of the lateral motions for the
$d$
of the lateral motions for the
![]() $O(\unicode[STIX]{x1D700})$
roots:
$O(\unicode[STIX]{x1D700})$
roots:
in view of (2.30), (3.7) and (3.9). Thus, while the vertical scale of these waves is small, they should have large sideways motions. Moreover, by (2.30), (3.7) and (3.12),
i.e. particles travel in large inertial circles of radius
![]() $b$
(or
$b$
(or
![]() $d$
) with very slight vertical motions. For the maximum possible amplitude wave (
$d$
) with very slight vertical motions. For the maximum possible amplitude wave (
![]() $a=1/m$
), the limiting lateral excursion would be
$a=1/m$
), the limiting lateral excursion would be
by (2.30), (3.7), (3.10), whereas the limiting longitudinal excursion is also
![]() $1/k$
:
$1/k$
:
due to (2.30), (3.7) and (3.14). However, given that these excursions must take place over an inertial period, implying huge velocities, the surface amplitude
![]() $a$
must be quite small relative to the (theoretically) maximum possible amplitude. Indeed, (2.12), (2.16) and (2.28) yield
$a$
must be quite small relative to the (theoretically) maximum possible amplitude. Indeed, (2.12), (2.16) and (2.28) yield
with
![]() $amc\approx ag/c_{0}$
due to (3.7) and (3.10), so that it is easily seen that the maximum particle velocity is
$amc\approx ag/c_{0}$
due to (3.7) and (3.10), so that it is easily seen that the maximum particle velocity is
Thus, choosing
![]() $\mathfrak{v}_{max}=1~\text{m}~\text{s}^{-1}$
and assuming that
$\mathfrak{v}_{max}=1~\text{m}~\text{s}^{-1}$
and assuming that
![]() $c_{0}=0.3~\text{m}~\text{s}^{-1}$
, the corresponding amplitude of the free surface deflection would be
$c_{0}=0.3~\text{m}~\text{s}^{-1}$
, the corresponding amplitude of the free surface deflection would be
![]() $a\approx 2~\text{cm}$
. For this velocity, the inertial circle radius would be approximately 5 km, in view of (3.13)–(3.15).
$a\approx 2~\text{cm}$
. For this velocity, the inertial circle radius would be approximately 5 km, in view of (3.13)–(3.15).
For the sake of comparison the small roots to
![]() $P(X)$
were computed numerically using the Matlab™ function ‘fzero’ which uses a combination of bisection, secant and inverse quadratic interpolation methods; see Forsythe, Malcolm & Moler (Reference Forsythe, Malcolm and Moler1976). A summary comparison of the perturbation expansion results for
$P(X)$
were computed numerically using the Matlab™ function ‘fzero’ which uses a combination of bisection, secant and inverse quadratic interpolation methods; see Forsythe, Malcolm & Moler (Reference Forsythe, Malcolm and Moler1976). A summary comparison of the perturbation expansion results for
![]() $c$
etc. with numerically determined values is given in figure 4. These results show that the perturbation expansion is remarkably accurate, something that is hardly surprising given that
$c$
etc. with numerically determined values is given in figure 4. These results show that the perturbation expansion is remarkably accurate, something that is hardly surprising given that
![]() $\unicode[STIX]{x1D700}$
is generally quite small.
$\unicode[STIX]{x1D700}$
is generally quite small.
We conclude our discussion of the wave motion induced by (2.7) by pointing out that the flow velocity is independent of the
![]() $y$
variable. Indeed, inverting the matrix in (2.11) yields
$y$
variable. Indeed, inverting the matrix in (2.11) yields
 $$\begin{eqnarray}\displaystyle & & \displaystyle \left(\begin{array}{@{}ccc@{}}\displaystyle \frac{\unicode[STIX]{x2202}q}{\unicode[STIX]{x2202}x} & \displaystyle \frac{\unicode[STIX]{x2202}r}{\unicode[STIX]{x2202}x} & \displaystyle \frac{\unicode[STIX]{x2202}s}{\unicode[STIX]{x2202}x}\\ \displaystyle \frac{\unicode[STIX]{x2202}q}{\unicode[STIX]{x2202}y} & \displaystyle \frac{\unicode[STIX]{x2202}r}{\unicode[STIX]{x2202}y} & \displaystyle \frac{\unicode[STIX]{x2202}s}{\unicode[STIX]{x2202}y}\\ \displaystyle \frac{\unicode[STIX]{x2202}q}{\unicode[STIX]{x2202}z} & \displaystyle \frac{\unicode[STIX]{x2202}r}{\unicode[STIX]{x2202}z} & \displaystyle \frac{\unicode[STIX]{x2202}s}{\unicode[STIX]{x2202}z}\end{array}\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\left(\begin{array}{@{}ccc@{}}\displaystyle \frac{1+am\,\text{e}^{\unicode[STIX]{x1D709}}\cos \unicode[STIX]{x1D703}}{1-a^{2}m^{2}\text{e}^{2\unicode[STIX]{x1D709}}} & -\displaystyle \frac{dk\,\text{e}^{\unicode[STIX]{x1D709}}\sin \unicode[STIX]{x1D703}}{1-a^{2}m^{2}\text{e}^{2\unicode[STIX]{x1D709}}} & \displaystyle \frac{ak\,\text{e}^{\unicode[STIX]{x1D709}}\sin \unicode[STIX]{x1D703}}{1-a^{2}m^{2}\text{e}^{2\unicode[STIX]{x1D709}}}\\ 0 & 1 & 0\\ -\,\displaystyle \frac{bm\,\text{e}^{\unicode[STIX]{x1D709}}\sin \unicode[STIX]{x1D703}}{1-a^{2}m^{2}\text{e}^{2\unicode[STIX]{x1D709}}} & -\displaystyle \frac{\text{d}m\,\text{e}^{\unicode[STIX]{x1D709}}\cos \unicode[STIX]{x1D703}-\text{d}m\,kb\,\text{e}^{2\unicode[STIX]{x1D709}}}{1-a^{2}m^{2}\text{e}^{2\unicode[STIX]{x1D709}}} & \displaystyle \frac{1-am\,\text{e}^{\unicode[STIX]{x1D709}}\cos \unicode[STIX]{x1D703}}{1-a^{2}m^{2}\text{e}^{2\unicode[STIX]{x1D709}}}\end{array}\right)\quad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \left(\begin{array}{@{}ccc@{}}\displaystyle \frac{\unicode[STIX]{x2202}q}{\unicode[STIX]{x2202}x} & \displaystyle \frac{\unicode[STIX]{x2202}r}{\unicode[STIX]{x2202}x} & \displaystyle \frac{\unicode[STIX]{x2202}s}{\unicode[STIX]{x2202}x}\\ \displaystyle \frac{\unicode[STIX]{x2202}q}{\unicode[STIX]{x2202}y} & \displaystyle \frac{\unicode[STIX]{x2202}r}{\unicode[STIX]{x2202}y} & \displaystyle \frac{\unicode[STIX]{x2202}s}{\unicode[STIX]{x2202}y}\\ \displaystyle \frac{\unicode[STIX]{x2202}q}{\unicode[STIX]{x2202}z} & \displaystyle \frac{\unicode[STIX]{x2202}r}{\unicode[STIX]{x2202}z} & \displaystyle \frac{\unicode[STIX]{x2202}s}{\unicode[STIX]{x2202}z}\end{array}\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\left(\begin{array}{@{}ccc@{}}\displaystyle \frac{1+am\,\text{e}^{\unicode[STIX]{x1D709}}\cos \unicode[STIX]{x1D703}}{1-a^{2}m^{2}\text{e}^{2\unicode[STIX]{x1D709}}} & -\displaystyle \frac{dk\,\text{e}^{\unicode[STIX]{x1D709}}\sin \unicode[STIX]{x1D703}}{1-a^{2}m^{2}\text{e}^{2\unicode[STIX]{x1D709}}} & \displaystyle \frac{ak\,\text{e}^{\unicode[STIX]{x1D709}}\sin \unicode[STIX]{x1D703}}{1-a^{2}m^{2}\text{e}^{2\unicode[STIX]{x1D709}}}\\ 0 & 1 & 0\\ -\,\displaystyle \frac{bm\,\text{e}^{\unicode[STIX]{x1D709}}\sin \unicode[STIX]{x1D703}}{1-a^{2}m^{2}\text{e}^{2\unicode[STIX]{x1D709}}} & -\displaystyle \frac{\text{d}m\,\text{e}^{\unicode[STIX]{x1D709}}\cos \unicode[STIX]{x1D703}-\text{d}m\,kb\,\text{e}^{2\unicode[STIX]{x1D709}}}{1-a^{2}m^{2}\text{e}^{2\unicode[STIX]{x1D709}}} & \displaystyle \frac{1-am\,\text{e}^{\unicode[STIX]{x1D709}}\cos \unicode[STIX]{x1D703}}{1-a^{2}m^{2}\text{e}^{2\unicode[STIX]{x1D709}}}\end{array}\right)\quad\end{eqnarray}$$
if we take (2.12)–(2.13) into account. Combining this with (2.16), by means of the change of variables
applied to each component of the fluid velocity yields
Note that (2.19) in conjunction with (2.30) ensure
so that in the absence of an underlying current the pressure is also independent of
![]() $y$
.
$y$
.

Figure 4. Plots of exact and approximate expressions for the (a) non-dimensional and (b) dimensional wave phase speeds, and dimensional vertical decay scale (c) and maximum horizontal wave displacement (d). Background conditions as in figure 2. In all four panels, the numerical solutions are shown with solid lines and the approximations given by equation (3.10) are shown with symbols.
4 Linear analysis
The linearized momentum and continuity equations for a wave–current interaction with an underlying uniform current propagating eastwards at the speed
![]() $c_{0}$
, in a homogeneous layer of water (whose density we normalize to unit value), are
$c_{0}$
, in a homogeneous layer of water (whose density we normalize to unit value), are
 $$\begin{eqnarray}\left.\begin{array}{@{}l@{}}u_{t}\,-c_{0}\,u_{x}+\hat{f}\,w-f\,v=-P_{x},\\ v_{t}-c_{0}\,v_{x}+f\,u=-P_{y},\\ w_{t}-c_{0}\,w_{x}-\hat{f}\,u=-P_{z}-g,\\ u_{x}+v_{y}+w_{z}=0.\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}l@{}}u_{t}\,-c_{0}\,u_{x}+\hat{f}\,w-f\,v=-P_{x},\\ v_{t}-c_{0}\,v_{x}+f\,u=-P_{y},\\ w_{t}-c_{0}\,w_{x}-\hat{f}\,u=-P_{z}-g,\\ u_{x}+v_{y}+w_{z}=0.\end{array}\right\}\end{eqnarray}$$
Assuming that the flow velocity is independent of
![]() $y$
, the exact boundary conditions on the surface
$y$
, the exact boundary conditions on the surface
![]() $z=\unicode[STIX]{x1D702}(x,y,t)$
are
$z=\unicode[STIX]{x1D702}(x,y,t)$
are
Linearization of (4.2) and transfer to
![]() $z=0$
gives
$z=0$
gives
The linearization of (4.3) is more complicated since we do not assume that the flow is irrotational. Constancy of the pressure of the free surface implies that the gradient of the pressure along the free surface defined by the tangent vector,
![]() $\unicode[STIX]{x1D749}$
, is zero:
$\unicode[STIX]{x1D749}$
, is zero:
Thus
To leading order, the dynamic boundary condition (4.3) is
For a flow velocity that is independent of
![]() $y$
, the last equation in (4.1) permits us to introduce a streamfunction
$y$
, the last equation in (4.1) permits us to introduce a streamfunction
![]() $\unicode[STIX]{x1D6F9}(x,z,t)$
, i.e.
$\unicode[STIX]{x1D6F9}(x,z,t)$
, i.e.
The
![]() $x$
- and
$x$
- and
![]() $z$
-momentum equations in (4.1) can be combined to produce
$z$
-momentum equations in (4.1) can be combined to produce
whereas differentiation of the
![]() $x$
-momentum equation with respect to
$x$
-momentum equation with respect to
![]() $y$
yields
$y$
yields
![]() $P_{xy}=0$
, allowing the
$P_{xy}=0$
, allowing the
![]() $y$
-momentum equation to be rewritten as follows, in a way that does not involve
$y$
-momentum equation to be rewritten as follows, in a way that does not involve
![]() $P$
:
$P$
:
We now seek travelling-wave solutions
with
![]() $m>0$
and
$m>0$
and
![]() $k>0$
, where the surface wave is defined as
$k>0$
, where the surface wave is defined as
Substitution of these forms into (4.10) produces the relation
where
is the wave phase speed relative to the underlying current. Likewise, (4.9) yields
Combining (4.13) and (4.15) results in
noting that
![]() $m$
is still unknown, as is
$m$
is still unknown, as is
![]() $c$
. The linearized kinematic free surface condition (4.4) connects
$c$
. The linearized kinematic free surface condition (4.4) connects
![]() $\unicode[STIX]{x1D6F9}$
and
$\unicode[STIX]{x1D6F9}$
and
![]() $\unicode[STIX]{x1D702}$
:
$\unicode[STIX]{x1D702}$
:
Finally, using (4.13) and (4.17), the linearized dynamic boundary condition (4.7) becomes
which gives
Note that choosing
![]() $f=\hat{f}=0$
and
$f=\hat{f}=0$
and
![]() $c_{0}=0$
, the classical deep water gravity-wave dispersion wave is recovered from (4.18), with
$c_{0}=0$
, the classical deep water gravity-wave dispersion wave is recovered from (4.18), with
![]() $c^{2}=g/k$
, since (4.16) would give
$c^{2}=g/k$
, since (4.16) would give
![]() $c=0$
unless
$c=0$
unless
![]() $m=k$
. On the other hand, multiplying (4.18) by
$m=k$
. On the other hand, multiplying (4.18) by
![]() $m$
and using (4.16), we find
$m$
and using (4.16), we find
which yields by (4.16), after squaring both sides, the quartic polynomial equation
allowing us to solve for
![]() $m>0$
in terms of
$m>0$
in terms of
![]() $k$
. If we make the above equation non-dimensional using
$k$
. If we make the above equation non-dimensional using
the equation for the dimensionless vertical decay scale is
The quartic polynomial
![]() $\mathfrak{P}$
in (4.23) has two positive roots between
$\mathfrak{P}$
in (4.23) has two positive roots between
![]() $1+\unicode[STIX]{x1D700}^{2}/2\pm \unicode[STIX]{x1D700}^{3}$
, since
$1+\unicode[STIX]{x1D700}^{2}/2\pm \unicode[STIX]{x1D700}^{3}$
, since
 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \mathfrak{P}(1+\unicode[STIX]{x1D700}^{2}/2-\unicode[STIX]{x1D700}^{3})>0,\\ \displaystyle \mathfrak{P}(1+\unicode[STIX]{x1D700}^{2}/2)=-\unicode[STIX]{x1D700}^{6}F^{2}+O(\unicode[STIX]{x1D700}^{8})<0,\\ \displaystyle \mathfrak{P}(1+\unicode[STIX]{x1D700}^{2}/2+\unicode[STIX]{x1D700}^{3})>0.\end{array}\right\} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \mathfrak{P}(1+\unicode[STIX]{x1D700}^{2}/2-\unicode[STIX]{x1D700}^{3})>0,\\ \displaystyle \mathfrak{P}(1+\unicode[STIX]{x1D700}^{2}/2)=-\unicode[STIX]{x1D700}^{6}F^{2}+O(\unicode[STIX]{x1D700}^{8})<0,\\ \displaystyle \mathfrak{P}(1+\unicode[STIX]{x1D700}^{2}/2+\unicode[STIX]{x1D700}^{3})>0.\end{array}\right\} & & \displaystyle\end{eqnarray}$$
Note that, by Viète’s formulas, the product of the four roots of
![]() $\mathfrak{P}$
is positive, while the sum of all possible subproducts, taken three at a time, is negative. This ensures that there are no further positive roots. Since only values
$\mathfrak{P}$
is positive, while the sum of all possible subproducts, taken three at a time, is negative. This ensures that there are no further positive roots. Since only values
![]() $\unicode[STIX]{x1D709}>0$
are physically relevant, we deduce that
$\unicode[STIX]{x1D709}>0$
are physically relevant, we deduce that
Substitution of (4.25) into (4.16) shows that
Therefore the linear analysis only identifies the ‘fast’ wave that is a standard deep water gravity wave modified very slightly by the Earth’s rotation.
5 Conclusions
The Lagrangian analysis we present shows that including rotation and mean currents yields Gerstner wave solutions like that of Pollard (Reference Pollard1970), excepting that we find that there are two kinds of waves possible. The first, described by Pollard, is a slightly modified Gerstner wave, that, like other Gerstner waves, does not have net wave transport and thus satisfies the steady state condition of no net transport on a rotating Earth given by Ursell (Reference Ursell1950) and Hasselmann (Reference Hasselmann1970). The second, much slower, type of wave motion requires a mean current in order that the vertical decay scale is finite; i.e. in the absence of currents, the second mode of motion would not be possible.
The second mode of motion, which we propose here to call an inertial Gerstner wave, produces waves that have extremely small vertical scales for gravity-wave wavelengths, while for very long wavelengths (thousands of km) it is one with waves with vertical decay scales of metres that can coexist with substantial currents even for relatively small amplitudes. At this time, we are unaware of any observations that might prove its existence, although given that it is at the inertial period it would be hard to detect using satellite methods (cf. White & Peterson Reference White and Peterson1996) since these tend to average out motions at time scales shorter than a few days at best. Likewise, given the ubiquity of inertial motions in the ocean, it might also be difficult to detect in data collected using fixed moorings (e.g. Gordon Reference Gordon and Sahrhage1988). Nonetheless, given that the inertial Gerstner wave is an exact solution to the Euler equations and one that satisfies the exact free surface conditions on the deformed free surface, it must be seen to represent a possible form of large-scale oceanic wave motion, and thus, ultimately may be important to the dynamics of energetic currents like the ACC.
Acknowledgement
The authors are grateful for helpful comments from the referees.
Appendix A
This appendix describes an analytic approach towards the identification of the location of the roots of the polynomial equation (2.38). Note that, due to the lack of significant surface waves at latitudes within
![]() $15^{\circ }$
from the poles, we have
$15^{\circ }$
from the poles, we have
![]() $|F|\geqslant 2-\sqrt{3}>0.25$
, while
$|F|\geqslant 2-\sqrt{3}>0.25$
, while
![]() $|F|<2.4$
outside the tropical zone (at latitudes that exceed
$|F|<2.4$
outside the tropical zone (at latitudes that exceed
![]() $23^{\circ }\,26^{\prime }\,16^{\prime \prime }$
), with
$23^{\circ }\,26^{\prime }\,16^{\prime \prime }$
), with
![]() $F>0$
in the Northern hemisphere, while
$F>0$
in the Northern hemisphere, while
![]() $F<0$
in the Southern hemisphere since
$F<0$
in the Southern hemisphere since
![]() $\hat{f}>0$
but
$\hat{f}>0$
but
![]() $f$
changes sign across the Equator.
$f$
changes sign across the Equator.
A.1 The case
 $c_{0}=0$
$c_{0}=0$
In this setting we recover the solution obtained by Pollard (Reference Pollard1970). If
![]() $X_{0}=0$
, then, as pointed out in § 2, the roots
$X_{0}=0$
, then, as pointed out in § 2, the roots
![]() $X=\pm \unicode[STIX]{x1D700}$
of (2.36) are ruled out, and of relevance are only the roots of the polynomial
$X=\pm \unicode[STIX]{x1D700}$
of (2.36) are ruled out, and of relevance are only the roots of the polynomial
obtained by factoring out the term
![]() $(X^{2}-\unicode[STIX]{x1D700}^{2})$
in (2.36).
$(X^{2}-\unicode[STIX]{x1D700}^{2})$
in (2.36).
Note that
![]() $P_{0}(0)=-1<0$
ensures the existence of at least one positive and one negative root of
$P_{0}(0)=-1<0$
ensures the existence of at least one positive and one negative root of
![]() $P_{0}$
. Computing the discriminant of the derivative polynomial
$P_{0}$
. Computing the discriminant of the derivative polynomial
as
we infer that
![]() $P_{0}^{\prime }$
has exactly one real root; see Prasolov (Reference Prasolov2010). Since between each pair of adjacent roots there must be a critical point, we deduce that
$P_{0}^{\prime }$
has exactly one real root; see Prasolov (Reference Prasolov2010). Since between each pair of adjacent roots there must be a critical point, we deduce that
![]() $P_{0}$
has exactly two real roots:
$P_{0}$
has exactly two real roots:
![]() $X_{0}^{-}<0$
and
$X_{0}^{-}<0$
and
![]() $X_{0}^{+}>0$
. Since
$X_{0}^{+}>0$
. Since
![]() $F=O(1)$
and
$F=O(1)$
and
![]() $\unicode[STIX]{x1D700}=O(10^{-4})$
, the estimates
$\unicode[STIX]{x1D700}=O(10^{-4})$
, the estimates
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle P_{0}(\pm 1)=\pm 2\unicode[STIX]{x1D700}F+O(\unicode[STIX]{x1D700}^{2}),\\ \displaystyle P_{0}(1-\unicode[STIX]{x1D700}F)=2\unicode[STIX]{x1D700}F+O(\unicode[STIX]{x1D700}^{2}),\\ \displaystyle P_{0}(-1-\unicode[STIX]{x1D700}F)=-2\unicode[STIX]{x1D700}F+O(\unicode[STIX]{x1D700}^{2}),\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle P_{0}(\pm 1)=\pm 2\unicode[STIX]{x1D700}F+O(\unicode[STIX]{x1D700}^{2}),\\ \displaystyle P_{0}(1-\unicode[STIX]{x1D700}F)=2\unicode[STIX]{x1D700}F+O(\unicode[STIX]{x1D700}^{2}),\\ \displaystyle P_{0}(-1-\unicode[STIX]{x1D700}F)=-2\unicode[STIX]{x1D700}F+O(\unicode[STIX]{x1D700}^{2}),\end{array}\right\}\end{eqnarray}$$
yield that at mid-latitudes (between
![]() $23^{\circ }\;26^{\prime }\;16^{\prime \prime }$
and
$23^{\circ }\;26^{\prime }\;16^{\prime \prime }$
and
![]() $75^{\circ }$
) we have:
$75^{\circ }$
) we have:
-
(i)
 $X_{0}^{-}+1\in (-\unicode[STIX]{x1D700}F,0)$
and
$X_{0}^{-}+1\in (-\unicode[STIX]{x1D700}F,0)$
and
 $X_{0}^{+}-1\in (-\unicode[STIX]{x1D700}F,0)$
in the Northern hemisphere;
$X_{0}^{+}-1\in (-\unicode[STIX]{x1D700}F,0)$
in the Northern hemisphere; -
(ii)
 $X_{0}^{-}+1\in (0,-\unicode[STIX]{x1D700}F)$
and
$X_{0}^{-}+1\in (0,-\unicode[STIX]{x1D700}F)$
and
 $X_{0}^{+}-1\in (0,-\unicode[STIX]{x1D700}F)$
in the Southern hemisphere.
$X_{0}^{+}-1\in (0,-\unicode[STIX]{x1D700}F)$
in the Southern hemisphere.
A.2 The case
 $c_{0}\neq 0$
$c_{0}\neq 0$
The third derivative of the polynomial in (2.38),
clearly has a negative discriminant, so that
![]() $P^{\prime }$
has exactly one real root and therefore
$P^{\prime }$
has exactly one real root and therefore
![]() $P$
has at most four real roots. Note that
$P$
has at most four real roots. Note that
![]() $P(0)>0$
, while from (2.36) we infer the estimates
$P(0)>0$
, while from (2.36) we infer the estimates
 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle P(\pm \unicode[STIX]{x1D700})=\unicode[STIX]{x1D700}^{4}X_{0}^{2}>0,\\ \displaystyle P(\pm (\unicode[STIX]{x1D700}+\unicode[STIX]{x1D700}^{3}X_{0}^{2}))=-\unicode[STIX]{x1D700}^{4}X_{0}^{2}+O(\unicode[STIX]{x1D700}^{5})<0,\\ \displaystyle P(\pm 1)=\pm 2\unicode[STIX]{x1D700}\,F\,(1\mp X_{0})+O(\unicode[STIX]{x1D700}^{2}),\\ \displaystyle P(\pm 1-\unicode[STIX]{x1D700}F(1\mp X_{0}))=\mp 2\unicode[STIX]{x1D700}\,F\,(1\mp X_{0})+O(\unicode[STIX]{x1D700}^{2}).\end{array}\right\} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle P(\pm \unicode[STIX]{x1D700})=\unicode[STIX]{x1D700}^{4}X_{0}^{2}>0,\\ \displaystyle P(\pm (\unicode[STIX]{x1D700}+\unicode[STIX]{x1D700}^{3}X_{0}^{2}))=-\unicode[STIX]{x1D700}^{4}X_{0}^{2}+O(\unicode[STIX]{x1D700}^{5})<0,\\ \displaystyle P(\pm 1)=\pm 2\unicode[STIX]{x1D700}\,F\,(1\mp X_{0})+O(\unicode[STIX]{x1D700}^{2}),\\ \displaystyle P(\pm 1-\unicode[STIX]{x1D700}F(1\mp X_{0}))=\mp 2\unicode[STIX]{x1D700}\,F\,(1\mp X_{0})+O(\unicode[STIX]{x1D700}^{2}).\end{array}\right\} & & \displaystyle\end{eqnarray}$$
Since
![]() $X_{0}=O(10^{-1})$
,
$X_{0}=O(10^{-1})$
,
![]() $\unicode[STIX]{x1D700}=O(10^{-4})$
and
$\unicode[STIX]{x1D700}=O(10^{-4})$
and
![]() $F=O(1)$
at mid-latitudes, we deduce that the polynomial
$F=O(1)$
at mid-latitudes, we deduce that the polynomial
![]() $P$
has exactly four real roots, two positive and two negative: a negative root in the interval
$P$
has exactly four real roots, two positive and two negative: a negative root in the interval
![]() $(-\unicode[STIX]{x1D700}-\unicode[STIX]{x1D700}^{3}X_{0}^{2},-\unicode[STIX]{x1D700})$
, a positive root in the interval
$(-\unicode[STIX]{x1D700}-\unicode[STIX]{x1D700}^{3}X_{0}^{2},-\unicode[STIX]{x1D700})$
, a positive root in the interval
![]() $(\unicode[STIX]{x1D700},\unicode[STIX]{x1D700}+\unicode[STIX]{x1D700}^{3}X_{0}^{2})$
and
$(\unicode[STIX]{x1D700},\unicode[STIX]{x1D700}+\unicode[STIX]{x1D700}^{3}X_{0}^{2})$
and
-
(i) a second negative root in the interval
 $(-1-\unicode[STIX]{x1D700}F(1+X_{0}),-1)$
and another positive root in the interval
$(-1-\unicode[STIX]{x1D700}F(1+X_{0}),-1)$
and another positive root in the interval
 $(1-\unicode[STIX]{x1D700}F(1-X_{0}),1)$
for
$(1-\unicode[STIX]{x1D700}F(1-X_{0}),1)$
for
 $F>0$
(in the Northern hemisphere);
$F>0$
(in the Northern hemisphere); -
(ii) a second negative in the interval
 $(-1,-1-\unicode[STIX]{x1D700}F(1+X_{0}))$
and another positive root in the interval
$(-1,-1-\unicode[STIX]{x1D700}F(1+X_{0}))$
and another positive root in the interval
 $(1,1-\unicode[STIX]{x1D700}F(1-X_{0}))$
for
$(1,1-\unicode[STIX]{x1D700}F(1-X_{0}))$
for
 $F<0$
(in the Southern hemisphere).
$F<0$
(in the Southern hemisphere).