Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Abdulameer, M.A.
Griffiths, P.T.
Alveroğlu, B.
and
Garrett, S.J.
2016.
On the stability of the BEK family of rotating boundary-layer flows for power-law fluids.
Journal of Non-Newtonian Fluid Mechanics,
Vol. 236,
Issue. ,
p.
63.
Imayama, Shintaro
Alfredsson, P. Henrik
and
Lingwood, R. J.
2016.
Experimental study of rotating-disk boundary-layer flow with surface roughness.
Journal of Fluid Mechanics,
Vol. 786,
Issue. ,
p.
5.
Appelquist, E.
Schlatter, P.
Alfredsson, P. H.
and
Lingwood, R. J.
2016.
On the global nonlinear instability of the rotating-disk flow over a finite domain.
Journal of Fluid Mechanics,
Vol. 803,
Issue. ,
p.
332.
Appelquist, E.
Imayama, Shintaro
Alfredsson, P. Henrik
Schlatter, P.
and
Lingwood, R.J.
2016.
Linear disturbances in the rotating-disk flow: A comparison between results from simulations, experiments and theory.
European Journal of Mechanics - B/Fluids,
Vol. 55,
Issue. ,
p.
170.
Ho, Joanna
Corke, Thomas C.
and
Matlis, Eric
2016.
Effect of wall suction on rotating disk absolute instability.
Journal of Fluid Mechanics,
Vol. 791,
Issue. ,
p.
704.
Lee, Keunseob
Nishio, Yu
Izawa, Seiichiro
and
Fukunishi, Yu
2017.
Effects of location of excitation on the spiral vortices in the transitional region of a rotating-disk flow.
Physics of Fluids,
Vol. 29,
Issue. 8,
Segalini, Antonio
and
Garrett, Stephen J.
2017.
On the non-parallel instability of the rotating-sphere boundary layer.
Journal of Fluid Mechanics,
Vol. 818,
Issue. ,
p.
288.
Thomas, Christian
and
Davies, Christopher
2018.
On the impulse response and global instability development of the infinite rotating-disc boundary layer.
Journal of Fluid Mechanics,
Vol. 857,
Issue. ,
p.
239.
Appelquist, E.
Schlatter, P.
Alfredsson, P. H.
and
Lingwood, R. J.
2018.
Transition to turbulence in the rotating-disk boundary-layer flow with stationary vortices.
Journal of Fluid Mechanics,
Vol. 836,
Issue. ,
p.
43.
Lee, K.
Nishio, Y.
Izawa, S.
and
Fukunishi, Y.
2018.
The effect of downstream turbulent region on the spiral vortex structures of a rotating-disk flow.
Journal of Fluid Mechanics,
Vol. 844,
Issue. ,
p.
274.
Tilton, Nils
and
Martinand, Denis
2018.
Taylor–Couette–Poiseuille flow with a weakly permeable inner cylinder: absolute instabilities and selection of global modes.
Journal of Fluid Mechanics,
Vol. 849,
Issue. ,
p.
741.
Yim, Eunok
Chomaz, J.-M.
Martinand, D.
and
Serre, E.
2018.
Transition to turbulence in the rotating disk boundary layer of a rotor–stator cavity.
Journal of Fluid Mechanics,
Vol. 848,
Issue. ,
p.
631.
Queguineur, Matthieu
Bridel-Bertomeu, Thibault
Gicquel, Laurent Y. M.
and
Staffelbach, Gabriel
2019.
Large eddy simulations and global stability analyses of an annular and cylindrical rotor/stator cavity limit cycles.
Physics of Fluids,
Vol. 31,
Issue. 10,
Thomas, Christian
and
Davies, Christopher
2019.
Global linear instability of rotating-cone boundary layers in a quiescent medium.
Physical Review Fluids,
Vol. 4,
Issue. 4,
Jing, Z.
and
Ducoin, A.
2020.
Direct numerical simulation and stability analysis of the transitional boundary layer on a marine propeller blade.
Physics of Fluids,
Vol. 32,
Issue. 12,
Thomas, Christian
and
Davies, Christopher
2021.
An adjoint approach for computing the receptivity of the rotating disc boundary layer to surface roughness.
Journal of Fluid Mechanics,
Vol. 926,
Issue. ,
Zhao, Zhizhou
Song, Wenwu
Jin, Yongxin
and
Lu, Jiaxing
2021.
Effect of Rotational Speed Variation on the Flow Characteristics in the Rotor-Stator System Cavity.
Applied Sciences,
Vol. 11,
Issue. 22,
p.
11000.
Morgan, Scott
Davies, Christopher
and
Thomas, Christian
2021.
Control of stationary convective instabilities in the rotating disk boundary layer via time-periodic modulation.
Journal of Fluid Mechanics,
Vol. 925,
Issue. ,
He, Xuerao
Sun, Zhihao
and
Zhang, Mengqi
2022.
Moffatt eddies in electrohydrodynamics flows: numerical simulations and analyses.
Journal of Fluid Mechanics,
Vol. 953,
Issue. ,
Morgan, Scott
Davies, Christopher
and
Thomas, Christian
2022.
Linear impulse response in three-dimensional oscillatory boundary layers formed by periodic modulation of a rotating disk.
Journal of Fluid Mechanics,
Vol. 949,
Issue. ,
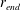 $r_{end}$ , by the modelled turbulence are included within the simulations, potentially allowing absolute instability to develop. During early times the flow shows traditional convective behaviour, with the total energy slowly decaying in time. However, after the disturbances have reached
$r_{end}$ , by the modelled turbulence are included within the simulations, potentially allowing absolute instability to develop. During early times the flow shows traditional convective behaviour, with the total energy slowly decaying in time. However, after the disturbances have reached 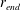 $r_{end}$ , the energy evolution reaches a turning point and, if the location of
$r_{end}$ , the energy evolution reaches a turning point and, if the location of 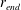 $r_{end}$ is at a Reynolds number larger than approximately
$r_{end}$ is at a Reynolds number larger than approximately 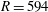 $R=594$ (radius non-dimensionalized by
$R=594$ (radius non-dimensionalized by 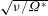 $\sqrt{{\it\nu}/{\rm\Omega}^{\ast }}$ , where
$\sqrt{{\it\nu}/{\rm\Omega}^{\ast }}$ , where  ${\it\nu}$ is the kinematic viscosity and
${\it\nu}$ is the kinematic viscosity and 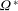 ${\rm\Omega}^{\ast }$ is the rotation rate of the disk), there will be global temporal growth. The global frequency and mode shape are clearly imposed by the conditions at
${\rm\Omega}^{\ast }$ is the rotation rate of the disk), there will be global temporal growth. The global frequency and mode shape are clearly imposed by the conditions at 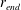 $r_{end}$ . Our results suggest that the linearized Ginzburg–Landau model by Healey (J. Fluid Mech., vol. 663, 2010, pp. 148–159) captures the (linear) physics of the developing rotating-disk flow, showing that there is linear global instability provided the Reynolds number of
$r_{end}$ . Our results suggest that the linearized Ginzburg–Landau model by Healey (J. Fluid Mech., vol. 663, 2010, pp. 148–159) captures the (linear) physics of the developing rotating-disk flow, showing that there is linear global instability provided the Reynolds number of 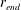 $r_{end}$ is sufficiently larger than the critical Reynolds number for the onset of absolute instability.
$r_{end}$ is sufficiently larger than the critical Reynolds number for the onset of absolute instability.

