Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Abdelbaki, A.R.
Païdoussis, M.P.
and
Misra, A.K.
2018.
A nonlinear model for a free-clamped cylinder subjected to confined axial flow.
Journal of Fluids and Structures,
Vol. 80,
Issue. ,
p.
390.
Jia, Kang
Fang, Le
and
Huang, Wei-Xi
2019.
Coupled states of dual side-by-side inverted flags in a uniform flow.
Journal of Fluids and Structures,
Vol. 91,
Issue. ,
p.
102768.
Yu, Yuelong
Liu, Yingzheng
and
Amandolese, Xavier
2019.
A Review on Fluid-Induced Flag Vibrations.
Applied Mechanics Reviews,
Vol. 71,
Issue. 1,
Gurugubelli, P.S.
and
Jaiman, R.K.
2019.
Large amplitude flapping of an inverted elastic foil in uniform flow with spanwise periodicity.
Journal of Fluids and Structures,
Vol. 90,
Issue. ,
p.
139.
Fan, Boyu
Huertas-Cerdeira, Cecilia
Cossé, Julia
Sader, John E.
and
Gharib, Morteza
2019.
Effect of morphology on the large-amplitude flapping dynamics of an inverted flag in a uniform flow.
Journal of Fluid Mechanics,
Vol. 874,
Issue. ,
p.
526.
Goza, Andres
Floryan, Daniel
and
Rowley, Clarence
2020.
Connections between resonance and nonlinearity in swimming performance of a flexible heaving plate.
Journal of Fluid Mechanics,
Vol. 888,
Issue. ,
Tavallaeinejad, Mohammad
Païdoussis, Michael P.
Legrand, Mathias
and
Kheiri, Mojtaba
2020.
Instability and the post-critical behaviour of two-dimensional inverted flags in axial flow.
Journal of Fluid Mechanics,
Vol. 890,
Issue. ,
Wang, Lei
Fang, Zhen
Hua, Ru-Nan
and
Peng, Ze-Rui
2020.
Numerical simulations of an inverted flexible plate in linear shear flows.
Physics of Fluids,
Vol. 32,
Issue. 4,
Tavallaeinejad, Mohammad
Païdoussis, Michael P.
Flores Salinas, Manuel
Legrand, Mathias
Kheiri, Mojtaba
and
Botez, Ruxandra M.
2020.
Flapping of heavy inverted flags: a fluid-elastic instability.
Journal of Fluid Mechanics,
Vol. 904,
Issue. ,
Mazharmanesh, Soudeh
Young, John
Tian, Fang-Bao
and
Lai, Joseph C.S.
2020.
Energy harvesting of two inverted piezoelectric flags in tandem, side-by-side and staggered arrangements.
International Journal of Heat and Fluid Flow,
Vol. 83,
Issue. ,
p.
108589.
Tavallaeinejad, Mohammad
Legrand, Mathias
and
Païdoussis, Michael P.
2020.
Nonlinear dynamics of slender inverted flags in uniform steady flows.
Journal of Sound and Vibration,
Vol. 467,
Issue. ,
p.
115048.
Chen, Yujia
Deng, Zhiwen
and
Liu, Yingzheng
2020.
Time-resolved particle image velocimetry measurement of vortex dynamics behind tandem self-oscillating inverted flags in a channel flow.
Experimental Thermal and Fluid Science,
Vol. 112,
Issue. ,
p.
109982.
Dorschner, Benedikt
and
Colonius, Tim
2020.
Immersed Boundary Method.
p.
3.
Pfister, J.-L.
and
Marquet, O.
2020.
Fluid–structure stability analyses and nonlinear dynamics of flexible splitter plates interacting with a circular cylinder flow.
Journal of Fluid Mechanics,
Vol. 896,
Issue. ,
Negi, P. S.
Hanifi, A.
and
Henningson, D. S.
2020.
On the linear global stability analysis of rigid-body motion fluid–structure-interaction problems.
Journal of Fluid Mechanics,
Vol. 903,
Issue. ,
He, Xin
Huang, Ning
Li, Xiaoping
and
Zhou, Yihao
2021.
Airflow‐induced high‐speed separation method for stacked paper labels and its mechanism.
Packaging Technology and Science,
Vol. 34,
Issue. 1,
p.
35.
Tavallaeinejad, Mohammad
Salinas, Manuel Flores
Païdoussis, Michael P.
Legrand, Mathias
Kheiri, Mojtaba
and
Botez, Ruxandra M.
2021.
Dynamics of inverted flags: Experiments and comparison with theory.
Journal of Fluids and Structures,
Vol. 101,
Issue. ,
p.
103199.
Yang, Kaidong
Nabawy, Mostafa R A
Cioncolini, Andrea
Revell, Alistair
and
AlGhrairy, Saad
2021.
Planform geometry effects of piezoelectric wind energy harvesting composite inverted flags.
Smart Materials and Structures,
Vol. 30,
Issue. 11,
p.
115014.
Mavroyiakoumou, Christiana
and
Alben, Silas
2021.
Eigenmode analysis of membrane stability in inviscid flow.
Physical Review Fluids,
Vol. 6,
Issue. 4,
Hiroaki, Keiichi
Hayashi, Yutaka
and
Watanabe, Masahiro
2021.
Numerical simulation on a limit cycle oscillation of a rectangular sheet in three-dimensional flow: influence of vortex element model on post-critical behavior.
Nonlinear Dynamics,
Vol. 106,
Issue. 4,
p.
2893.
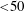 ${<}50$) and is not classical VIV. Finally, with respect to point (iii), chaotic flapping has been observed experimentally for Reynolds numbers of
${<}50$) and is not classical VIV. Finally, with respect to point (iii), chaotic flapping has been observed experimentally for Reynolds numbers of 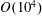 $O(10^{4})$, and here we show that chaos also persists at a moderate Reynolds number of 200. We characterise this chaotic regime and calculate its strange attractor, whose structure is controlled by the above-mentioned deformed equilibria and is similar to a Lorenz attractor.
$O(10^{4})$, and here we show that chaos also persists at a moderate Reynolds number of 200. We characterise this chaotic regime and calculate its strange attractor, whose structure is controlled by the above-mentioned deformed equilibria and is similar to a Lorenz attractor.

