Article contents
Global vorticity shedding for a vanishing wing
Published online by Cambridge University Press: 13 February 2012
Abstract
If a moving body were made to vanish within a fluid, its boundary-layer vorticity would be released into the fluid at all locations simultaneously, a phenomenon we call global vorticity shedding. We approximate this process by studying the related problem of rapid vorticity transfer from the boundary layer of a body undergoing a quick change of cross-sectional and surface area. A surface-piercing foil is first towed through water at constant speed, 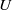 , and constant angle of attack, then rapidly pulled out of the fluid in the spanwise direction. Viewed within a fixed plane perpendicular to the span, the cross-sectional area of the foil seemingly disappears. The rapid spanwise motion results in the nearly instantaneous shedding of the boundary layer into the surrounding fluid. Particle image velocimetry measurements show that the shed layers quickly transition from free shear layers to form two strong, unequal-strength vortices, formed within non-dimensional time
, and constant angle of attack, then rapidly pulled out of the fluid in the spanwise direction. Viewed within a fixed plane perpendicular to the span, the cross-sectional area of the foil seemingly disappears. The rapid spanwise motion results in the nearly instantaneous shedding of the boundary layer into the surrounding fluid. Particle image velocimetry measurements show that the shed layers quickly transition from free shear layers to form two strong, unequal-strength vortices, formed within non-dimensional time 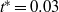 , based on the foil chord and forward velocity. These vortices are connected to, and interact with, the foil’s tip vortex through additional streamwise vorticity formed during the rapid pulling of the foil. Numerical simulations show that two strong spanwise vortices form from the shed vorticity of the boundary layer. The three-dimensional effects of the foil removal process are restricted to the tip of the foil. This method of vorticity transfer may be used for quickly introducing circulation to a fluid to provide forcing for biologically inspired flow control.
, based on the foil chord and forward velocity. These vortices are connected to, and interact with, the foil’s tip vortex through additional streamwise vorticity formed during the rapid pulling of the foil. Numerical simulations show that two strong spanwise vortices form from the shed vorticity of the boundary layer. The three-dimensional effects of the foil removal process are restricted to the tip of the foil. This method of vorticity transfer may be used for quickly introducing circulation to a fluid to provide forcing for biologically inspired flow control.
Information
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2011
References
- 22
- Cited by

