Andres, J. T. H. & Cardoso, S. S. S.
2011
Onset of convection in a porous medium in the presence of chemical reaction. Phys. Rev. E
83, 046312.
Andres, J. T. H. & Cardoso, S. S. S.
2012
Convection and reaction in a diffusive boundary layer in a porous medium: nonlinear dynamics. Chaos
22 (3), 037113.
Asselin, R.
1972
Frequency filter for time integrations. Mon. Weath. Rev.
100 (6), 487–490.
Bestehorn, M. & Firoozabadi, A.
2012
Effect of fluctuations on the onset of density-driven convection in porous media. Phys. Fluids
24, 114102.
Boyd, J. P.
2001
Chebyshev and Fourier Spectral Methods. Dover.
Daniel, D., Tilton, N. & Riaz, A.
2013
Optimal perturbations of gravitationally unstable, transient boundary layers in porous media. J. Fluid Mech.
727, 456–487.
Ennis-King, J. & Paterson, L.
2007
Coupling of geochemical reactions and convective mixing in the long-term geological storage of carbon dioxide. Intl J. Greenh. Gas Control
1, 86–93.
Fu, X., Cueto-Felgueroso, L. & Juanes, R.
2013
Pattern formation and coarsening dynamics in three-dimensional convective mixing in porous media. Phil. Trans. R. Soc. A
371 (2004), 20120355.
Ghesmat, K., Hassanzadeh, H. & Abedi, J.
2009
The impact of geochemistry on convective mixing in a gravitationally unstable diffusive boundary layer in porous media:
$\text{CO}_{2}$
storage in saline aquifers. J. Fluid Mech.
673, 480–512.
Graham, M. D. & Steen, P. H.
1994
Plume formation and resonant bifurcations in porous-media convection. J. Fluid Mech.
272, 67–90.
Hewitt, D. R., Neufeld, J. A. & Lister, J. R.
2012
Ultimate regime of high Rayleigh number convection in a porous medium. Phys. Rev. Lett.
108, 224503.
Hewitt, D. R., Neufeld, J. A. & Lister, J. R.
2013a
Convective shutdown in a porous medium at high Rayleigh number. J. Fluid Mech.
719, 551–586.
Hewitt, D. R., Neufeld, J. A. & Lister, J. R.
2013b
Stability of columnar convection in a porous medium. J. Fluid Mech.
737, 205–231.
Hewitt, D. R., Neufeld, J. A. & Lister, J. R.
2014
High Rayleigh number convection in a three-dimensional porous medium. J. Fluid Mech.
748, 879–895.
Hidalgo, J. J., Fe, J., Cueto-Felgueroso, L. & Juanes, R.
2012
Scaling of convective mixing in porous media. Phys. Rev. Lett.
109, 264503.
Howard, L. N.
1964
Convection at high Rayleigh number. In Applied Mechanics, Proceedings of the 11th Congress of Applied Mechanics (ed. Görtler, H.), pp. 1109–1115. Springer.
Huppert, H. E. & Neufeld, J. A.
2014
The fluid mechanics of carbon dioxide sequestration. Annu. Rev. Fluid Mech.
46, 255–272.
Malkus, W. V. R.
1954
The heat transport and spectrum of thermal turbulence. Proc. R. Soc. Lond. A
225, 196–212.
Mitchell, M. J., Jensen, O. E., Cliffe, K. A. & Maroto-Valer, M. M.
2010
A model of carbon dioxide dissolution and mineral carbonation kinetics. Proc. R. Soc. Lond. A
466, 1265–1290.
Myint, P. C. & Firoozabadi, A.
2013
Onset of buoyancy-driven convection in Cartesian and cylindrical geometries. Phys. Fluids
25 (4), 044105.
Neufeld, J. A., Hesse, M. A., Riaz, A., Hallworth, M. A., Tchelepi, H. A. & Huppert, H. E.
2010
Convective dissolution of carbon dioxide in saline aquifers. Geophys. Res. Lett.
37, L22404.
Otero, J., Dontcheva, L. A., Johnston, H., Worthing, R. A., Kurganov, A., Petrova, G. & Doering, C. R.
2004
High-Rayleigh-number convection in a fluid-saturated porous layer. J. Fluid Mech.
500, 263–281.
Pau, G. S. H., Bell, J. B., Pruess, K., Almgren, A. S., Lijewski, M. J. & Zhang, K.
2010
High-resolution simulation and characterization of density-driven flow in
$\text{CO}_{2}$
storage in saline aquifers. Adv. Water Resour.
33, 443–455.
Rapaka, S., Chen, S., Pawar, R. J., Stauffer, P. H. & Zhang, D.
2008
Non-modal growth of perturbations in density-driven convection in porous media. J. Fluid Mech.
609, 285–303.
Rapaka, S., Pawar, R. J., Stauffer, P. H., Zhang, D. & Chen, S.
2009
Onset of convection over a transient base-state in anisotropic and layered porous media. J. Fluid Mech.
641, 227–244.
Rees, D. A. S., Selim, A. & Ennis-King, J. P.
2008
The instability of unsteady boundary layers in porous media. In Emerging Topics in Heat and Mass Transfer in Porous Media, pp. 85–110. Springer.
Riaz, A., Hesse, M., Tchelepi, H. A. & Orr, F. M.
2006
Onset of convection in a gravitationally unstable diffusive boundary layer in porous media. J. Fluid Mech.
548, 87–111.
Ritchie, L. T. & Pritchard, D.
2011
Natural convection and the evolution of a reactive porous medium. J. Fluid Mech.
673, 286–317.
Schmid, P. J.
2007
Nonmodal stability theory. Annu. Rev. Fluid Mech.
39, 129–162.
Slim, A. C.
2014
Solutal-convection regimes in a two-dimensional porous medium. J. Fluid Mech.
741, 461–491.
Slim, A. C., Bandi, M. M., Miller, J. C. & Mahadevan, L.
2013
Dissolution-driven convection in a Hele-Shaw cell. Phys. Fluids
25, 024101.
Szulczewski, M. L., Hesse, M. A. & Juanes, R.
2013
Carbon dioxide dissolution in structural and stratigraphic traps. J. Fluid Mech.
736, 287–315.
Tilton, N., Daniel, D. & Riaz, A.
2013
The initial transient period of gravitationally unstable diffusive boundary layers developing in porous media. Phys. Fluids
25 (9), 092107.
Tilton, N. & Riaz, A.
2014
Nonlinear stability of gravitationally unstable, transient, diffusive boundary layers in porous media. J. Fluid Mech.
745, 251–278.
Trefethen, L. N.
2000
Spectral Methods in MATLAB. SIAM.
Ward, T. J., Cliffe, K. A., Jensen, O. E. & Power, H.
2014
Dissolution-driven porous-medium convection in the presence of chemical reaction. J. Fluid Mech.
747, 316–349.
Wen, B., Chini, G. P., Dianati, N. & Doering, C. R.
2013
Computational approaches to aspect-ratio-dependent upper bounds and heat flux in porous medium convection. Phys. Lett. A
377 (41), 2931–2938.
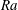$\mathit{Ra}$
, in which the domain is considered deep, shallow or of intermediate depth, and for which the Damköhler number
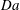$\mathit{Da}$
is respectively large, small or of order unity. Scaling properties of the flow are identified numerically and rationalised via the analytic model. For fully established high-
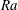$\mathit{Ra}$
convection, analysis and simulation suggest that the time-averaged solute transfer rate scales with
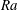$\mathit{Ra}$
and the plume horizontal wavenumber with
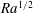$\mathit{Ra}^{1/2}$
, with coefficients modulated by
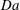$\mathit{Da}$
in each case. For large
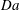$\mathit{Da}$
, the rapid reaction rate limits the plume depth and the boundary layer restricts the rate of solute transfer to the bulk, whereas for small
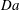$\mathit{Da}$
the average solute transfer rate is ultimately limited by the domain depth and the convection is correspondingly weaker.
$\text{CO}_{2}$
storage in saline aquifers. J. Fluid Mech.
673, 480–512.
$\text{CO}_{2}$
storage in saline aquifers. Adv. Water Resour.
33, 443–455.
