1. Introduction
Molland & Turnock (Reference Molland and Turnock2022, Chapter 4) define a hydrofoil as a lifting surface that operates in water. They note that the recent adoption of high-performance materials like carbon-fibre composites has led to new applications in hydrofoil-supported commercial craft, hydrofoil-supported yachts, yacht keels and hydroplanes, and observe that while the performance of deeply submerged foils is similar to that of lifting surfaces in unbounded domains, the performance of near-surface hydrofoils is determined primarily by their distance below the surface and the Froude number of the flow – the ratio of the foil speed to a typical surface wave speed. At moderate Froude number, surface wave generation determines the drag on a foil. Semenov & Wu (Reference Semenov and Wu2020, SW20 herein) give a comprehensive description of past investigations into wave generation by steadily advancing, submerged bodies before presenting a reduction of the full nonlinear problem for irrotational, non-separated, two-dimensional flow past an arbitrary body to an integral equation that they solve numerically at a selection of Froude numbers and depths of submergence for flow past both a thin hydrofoil and a submerged cylinder with and without gravity.
Analytical treatments have restricted attention either to depths of submergence sufficiently large for the amplitude of any forced free-surface waves to be sufficiently small that the surface boundary condition can be expanded in wave amplitude, or to flows where the Froude number is sufficiently large that gravity can be neglected at leading order. This latter limit is considered here for the irrotational, two-dimensional flow past a flat-plate foil. Gurevitch (Reference Gurevitch1965, § 34) summarises theoretical work on this problem and notes that he is unaware of any complete solution. Analytical progress to that date had been made by assuming that a cavitation zone extended from the foil to downstream infinity, so rendering the flow domain singly connected and susceptible to treatment by a hodograph method. The present work gives closed-form analytical solutions for attached flow for arbitrary depths of submergence and angles of attack.
Section 2 formulates the problem. Section 3 obtains the solution using a method related to that of Michell (Reference Michell1890) and Joukovskii (Reference Joukovskii1890). The doubly connected flow domain, in the complex ![]() $z$-plane, is conformally mapped, by a mapping to be determined, to a concentric annulus in an auxiliary complex
$z$-plane, is conformally mapped, by a mapping to be determined, to a concentric annulus in an auxiliary complex ![]() $\zeta$-plane. The complex flow potential
$\zeta$-plane. The complex flow potential ![]() $w(z)$ and its derivative
$w(z)$ and its derivative ![]() $w'(z)$ are obtained in terms of
$w'(z)$ are obtained in terms of ![]() $\zeta$ by considering their forms at known points in the flow, as in Chaplygin's method of special points Gurevitch (Reference Gurevitch1965, § 5). The required conformal mapping is then determined here by explicit integration. Crowdy & Green (Reference Crowdy and Green2011), Crowdy, Llewellyn Smith & Freilich (Reference Crowdy, Llewellyn Smith and Freilich2013) and subsequent co-workers use this method to discuss hollow vortices, and SW20 use a similar procedure to obtain their integral equation. Section 4 shows that in this limit, due to the absence of surface waves and separation, the drag on the foil vanishes and obtains the lift as a function of the angle of attack and depth of submergence. Section 5 gives the form of the solution in the limiting cases of horizontal and near-vertical foils. Section 6 describes surface profiles, flow patterns and force predictions, comparing them with the computations at large Froude number in SW20 where relevant. A reader who is interested mainly in the properties of the flow solutions obtained could initially omit the analytical details of §§ 2–5 and begin at § 6. Section 7 summarises the minimum numerical computation required to obtain the lift coefficient and reproduce the examples presented in § 6, and then briefly discusses the results.
$\zeta$ by considering their forms at known points in the flow, as in Chaplygin's method of special points Gurevitch (Reference Gurevitch1965, § 5). The required conformal mapping is then determined here by explicit integration. Crowdy & Green (Reference Crowdy and Green2011), Crowdy, Llewellyn Smith & Freilich (Reference Crowdy, Llewellyn Smith and Freilich2013) and subsequent co-workers use this method to discuss hollow vortices, and SW20 use a similar procedure to obtain their integral equation. Section 4 shows that in this limit, due to the absence of surface waves and separation, the drag on the foil vanishes and obtains the lift as a function of the angle of attack and depth of submergence. Section 5 gives the form of the solution in the limiting cases of horizontal and near-vertical foils. Section 6 describes surface profiles, flow patterns and force predictions, comparing them with the computations at large Froude number in SW20 where relevant. A reader who is interested mainly in the properties of the flow solutions obtained could initially omit the analytical details of §§ 2–5 and begin at § 6. Section 7 summarises the minimum numerical computation required to obtain the lift coefficient and reproduce the examples presented in § 6, and then briefly discusses the results.
2. Problem formulation
We consider the planar, steady, free-surface flow of a fluid of infinite depth past a submerged hydrofoil, which we model as a straight-line segment of finite length. We assume the fluid to be inviscid and incompressible, and the flow to be irrotational. We also assume an infinite Froude number, i.e. we ignore the effect of gravity on the free surface. We consider the flow domain to lie in a complex ![]() $z$-plane, where
$z$-plane, where ![]() $z=x+\mathrm {i}y$. We denote this domain by
$z=x+\mathrm {i}y$. We denote this domain by ![]() $D$. We denote the free surface of
$D$. We denote the free surface of ![]() $D$ by
$D$ by ![]() $\partial D_0$, and the boundary of the hydrofoil by
$\partial D_0$, and the boundary of the hydrofoil by ![]() $\partial D_1$. An example is sketched in figure 1. We represent the velocity field of the flow by the vector
$\partial D_1$. An example is sketched in figure 1. We represent the velocity field of the flow by the vector ![]() $(u(x,y),v(x,y))$. We assume that at infinity, the flow is uniform and in the positive
$(u(x,y),v(x,y))$. We assume that at infinity, the flow is uniform and in the positive ![]() $x$-direction, i.e. to leading order,
$x$-direction, i.e. to leading order, ![]() $(u(x,y),v(x,y))\sim (U,0)$, for some real constant
$(u(x,y),v(x,y))\sim (U,0)$, for some real constant ![]() $U>0$. The shape of
$U>0$. The shape of ![]() $\partial D_0$ is unknown a priori but will be determined as part of our solution.
$\partial D_0$ is unknown a priori but will be determined as part of our solution.

Figure 1. Sketch of the flow domain ![]() $D$ for a free-surface flow past a submerged hydrofoil. Here,
$D$ for a free-surface flow past a submerged hydrofoil. Here, ![]() $\partial D_0$ denotes the free surface (in blue) while
$\partial D_0$ denotes the free surface (in blue) while ![]() $\partial D_1$ denotes the hydrofoil (red). Also,
$\partial D_1$ denotes the hydrofoil (red). Also, ![]() $z_1=0$ and
$z_1=0$ and ![]() $z_2=\mathrm {e}^{\mathrm {i}\alpha }$ denote, respectively, the leading and trailing edges of the hydrofoil, so
$z_2=\mathrm {e}^{\mathrm {i}\alpha }$ denote, respectively, the leading and trailing edges of the hydrofoil, so ![]() $-\alpha$ gives the angle of attack, and
$-\alpha$ gives the angle of attack, and ![]() $z_3$ denotes a stagnation point – this lies on the leading face of the hydrofoil.
$z_3$ denotes a stagnation point – this lies on the leading face of the hydrofoil.
Without loss of generality, we may normalise the hydrofoil to be of unit length, and fix its leading endpoint to be at the origin. We denote this endpoint by ![]() $z_1$. We denote the trailing endpoint of the foil by
$z_1$. We denote the trailing endpoint of the foil by ![]() $z_2$. Then
$z_2$. Then ![]() $z_2=\mathrm {e}^{\mathrm {i}\alpha }$ (so the angle of attack is
$z_2=\mathrm {e}^{\mathrm {i}\alpha }$ (so the angle of attack is ![]() $-\alpha$), where we consider
$-\alpha$), where we consider ![]() $\alpha$ over the range
$\alpha$ over the range ![]() $(-{\rm \pi} /2,{\rm \pi} /2)$. The case of a horizontal hydrofoil – i.e.
$(-{\rm \pi} /2,{\rm \pi} /2)$. The case of a horizontal hydrofoil – i.e. ![]() $\alpha =0$ – is trivial (the hydrofoil does not disturb the flow past it), thus we henceforth ignore it (although we will retrieve it later as a limiting case of our results – see § 5.1). We will also not consider a vertical hydrofoil, i.e.
$\alpha =0$ – is trivial (the hydrofoil does not disturb the flow past it), thus we henceforth ignore it (although we will retrieve it later as a limiting case of our results – see § 5.1). We will also not consider a vertical hydrofoil, i.e. ![]() $\alpha =\pm {\rm \pi}/2$; this is because our analysis relies on there being a trailing endpoint (we will be imposing the Kutta condition there). (However, we will present the limits of our results as
$\alpha =\pm {\rm \pi}/2$; this is because our analysis relies on there being a trailing endpoint (we will be imposing the Kutta condition there). (However, we will present the limits of our results as ![]() $\alpha \rightarrow \pm {\rm \pi}/2$ – see § 5.2.) For the example sketched in figure 1,
$\alpha \rightarrow \pm {\rm \pi}/2$ – see § 5.2.) For the example sketched in figure 1, ![]() $-{\rm \pi} /2<\alpha <0$, so the hydrofoil slopes downwards from its leading endpoint to its trailing endpoint.
$-{\rm \pi} /2<\alpha <0$, so the hydrofoil slopes downwards from its leading endpoint to its trailing endpoint.
We can define a complex potential ![]() $w(z)=\phi (x,y)+\mathrm {i}\,\psi (x,y)$ for the flow, where
$w(z)=\phi (x,y)+\mathrm {i}\,\psi (x,y)$ for the flow, where ![]() $\phi (x,y)$ and
$\phi (x,y)$ and ![]() $\psi (x,y)$ are the associated velocity potential and streamfunction, respectively.
$\psi (x,y)$ are the associated velocity potential and streamfunction, respectively. ![]() $w(z)$ possesses the following properties. It is analytic in the interior of
$w(z)$ possesses the following properties. It is analytic in the interior of ![]() $D$, and
$D$, and ![]() $w'(z)=u(x,y)-\mathrm {i}\,v(x,y)$ gives the complex velocity, where here and throughout this paper we use
$w'(z)=u(x,y)-\mathrm {i}\,v(x,y)$ gives the complex velocity, where here and throughout this paper we use ![]() $'$ to indicate the derivative of a function of one variable. It follows from our above assumption of uniform flow at infinity that, to leading order,
$'$ to indicate the derivative of a function of one variable. It follows from our above assumption of uniform flow at infinity that, to leading order,
Next, since ![]() $\partial D_0$ and
$\partial D_0$ and ![]() $\partial D_1$ are both streamlines of the flow (of course, strictly speaking,
$\partial D_1$ are both streamlines of the flow (of course, strictly speaking, ![]() $\partial D_1$ is just part of the streamline that lies along it),
$\partial D_1$ is just part of the streamline that lies along it), ![]() $\mathrm {Im}\{w(z)\}$ must be constant along them, i.e.
$\mathrm {Im}\{w(z)\}$ must be constant along them, i.e.
for some constants ![]() $\psi _0$ and
$\psi _0$ and ![]() $\psi _1$. For the same reason, one may deduce that
$\psi _1$. For the same reason, one may deduce that
Furthermore, it follows from Bernoulli's equation and our assumption of an infinite Froude number that
In addition, one may deduce that for ![]() $z$ local to the leading endpoint
$z$ local to the leading endpoint ![]() $z_1$ (
$z_1$ (![]() $=0$) of the hydrofoil, to leading order,
$=0$) of the hydrofoil, to leading order,
for some constant ![]() $A$. Thus the velocity field is singular at
$A$. Thus the velocity field is singular at ![]() $z_1$. To ensure that the velocity field is bounded at the trailing endpoint
$z_1$. To ensure that the velocity field is bounded at the trailing endpoint ![]() $z_2$, we impose the Kutta condition there, thus assuming a certain circulation
$z_2$, we impose the Kutta condition there, thus assuming a certain circulation ![]() $\varGamma$, say, around the hydrofoil so
$\varGamma$, say, around the hydrofoil so
where ![]() $\mathcal {C}$ is a simple closed contour that surrounds the hydrofoil, and we integrate around
$\mathcal {C}$ is a simple closed contour that surrounds the hydrofoil, and we integrate around ![]() $\mathcal {C}$ in the anticlockwise direction. Finally, one may also deduce that there must be a stagnation point of the flow at some point
$\mathcal {C}$ in the anticlockwise direction. Finally, one may also deduce that there must be a stagnation point of the flow at some point ![]() $z_3$ on the leading face of the hydrofoil. More specifically, one may deduce that for
$z_3$ on the leading face of the hydrofoil. More specifically, one may deduce that for ![]() $z$ local to
$z$ local to ![]() $z_3$, to leading order,
$z_3$, to leading order,
for some constant ![]() $B$. We assume this to be the only stagnation point of the flow;
$B$. We assume this to be the only stagnation point of the flow; ![]() $z_3$ will not coincide with the leading endpoint
$z_3$ will not coincide with the leading endpoint ![]() $z_1$ except in the case when the hydrofoil is horizontal, which (as stated above) we will ignore.
$z_1$ except in the case when the hydrofoil is horizontal, which (as stated above) we will ignore.
3. A conformal parametrisation
We will seek ![]() $D$ (which is a doubly connected domain) as the image of a concentric annulus
$D$ (which is a doubly connected domain) as the image of a concentric annulus ![]() $D_{\zeta }$ in a complex
$D_{\zeta }$ in a complex ![]() $\zeta$-plane, under a one-to-one conformal map, which we denote by
$\zeta$-plane, under a one-to-one conformal map, which we denote by ![]() $z(\zeta )$. Such a parametrisation is known to exist by Koebe's extension of Riemann's mapping theorem (e.g. see Goluzin Reference Goluzin1969). Without loss of generality, we may take
$z(\zeta )$. Such a parametrisation is known to exist by Koebe's extension of Riemann's mapping theorem (e.g. see Goluzin Reference Goluzin1969). Without loss of generality, we may take ![]() $D_{\zeta }$ to be the annular domain that is bounded by the circles
$D_{\zeta }$ to be the annular domain that is bounded by the circles ![]() $C_0$ and
$C_0$ and ![]() $C_1$, which are both centred on the origin and have radii
$C_1$, which are both centred on the origin and have radii ![]() $1$ and
$1$ and ![]() $q$, respectively, for some
$q$, respectively, for some ![]() $q$ with
$q$ with ![]() $0< q<1$, and assume that
$0< q<1$, and assume that ![]() $\partial D_j$ is the image under
$\partial D_j$ is the image under ![]() $z(\zeta )$ of
$z(\zeta )$ of ![]() $C_j$, for
$C_j$, for ![]() $j=0,1$. Furthermore, we may assume that the point at infinity in the
$j=0,1$. Furthermore, we may assume that the point at infinity in the ![]() $z$-plane is the image of
$z$-plane is the image of ![]() $\zeta =-\mathrm {i}$, and, more specifically, that for
$\zeta =-\mathrm {i}$, and, more specifically, that for ![]() $\zeta$ local to
$\zeta$ local to ![]() $-\mathrm {i}$, to leading order,
$-\mathrm {i}$, to leading order,
for some real constant ![]() $a>0$. Finally, for
$a>0$. Finally, for ![]() $j=1,2,3$, we denote the pre-image of
$j=1,2,3$, we denote the pre-image of ![]() $z_j$ by
$z_j$ by ![]() $\zeta _j$, which lies on
$\zeta _j$, which lies on ![]() $C_1$. For a given hydrofoil, having made the assumptions on
$C_1$. For a given hydrofoil, having made the assumptions on ![]() $z(\zeta )$ that are listed above, we are not at liberty to choose
$z(\zeta )$ that are listed above, we are not at liberty to choose ![]() $\zeta _j$,
$\zeta _j$, ![]() $j=1,2,3$; instead, we must solve for these, as explained below. One may deduce (on purely geometrical grounds) that
$j=1,2,3$; instead, we must solve for these, as explained below. One may deduce (on purely geometrical grounds) that ![]() $z'(\zeta )$ has simple zeros at both
$z'(\zeta )$ has simple zeros at both ![]() $\zeta =\zeta _1$ and
$\zeta =\zeta _1$ and ![]() $\zeta _2$. An example is sketched in figure 2. Here,
$\zeta _2$. An example is sketched in figure 2. Here, ![]() $\zeta _3$ lies on the section of
$\zeta _3$ lies on the section of ![]() $C_1$ that is traversed in passing from
$C_1$ that is traversed in passing from ![]() $\zeta _1$ to
$\zeta _1$ to ![]() $\zeta _2$ in the anticlockwise direction, which is the case for a hydrofoil that slopes downwards from its leading endpoint to its trailing endpoint. However, our subsequent analysis makes no assumption on the ordering of
$\zeta _2$ in the anticlockwise direction, which is the case for a hydrofoil that slopes downwards from its leading endpoint to its trailing endpoint. However, our subsequent analysis makes no assumption on the ordering of ![]() $\zeta _1$,
$\zeta _1$, ![]() $\zeta _2$ and
$\zeta _2$ and ![]() $\zeta _3$ around
$\zeta _3$ around ![]() $C_1$.
$C_1$.

Figure 2. Sketch of the pre-image domain ![]() $D_{\zeta }$ for our conformal parametrisation of the flow domain
$D_{\zeta }$ for our conformal parametrisation of the flow domain ![]() $D$ as in figure 1. Here,
$D$ as in figure 1. Here, ![]() $D$ is the image of
$D$ is the image of ![]() $D_{\zeta }$ under a conformal map
$D_{\zeta }$ under a conformal map ![]() $z(\zeta )$.
$z(\zeta )$.
Now, in terms of ![]() $\zeta$, we have
$\zeta$, we have
for some functions ![]() $W$, the complex potential in
$W$, the complex potential in ![]() $D_{\zeta }$, and
$D_{\zeta }$, and ![]() $\varOmega$, the complex velocity mapped to
$\varOmega$, the complex velocity mapped to ![]() $D_{\zeta }$ . We construct below formulae (in terms of
$D_{\zeta }$ . We construct below formulae (in terms of ![]() $\zeta$) for
$\zeta$) for ![]() $W(\zeta )$,
$W(\zeta )$, ![]() $\varOmega (\zeta )$, and then make use of the fact that (Joukovskii Reference Joukovskii1890; Michell Reference Michell1890)
$\varOmega (\zeta )$, and then make use of the fact that (Joukovskii Reference Joukovskii1890; Michell Reference Michell1890)
to construct a formula for ![]() $z(\zeta )$. A similar construction is used to obtain the hollow vortex solutions in Crowdy & Green (Reference Crowdy and Green2011) and Crowdy et al. (Reference Crowdy, Llewellyn Smith and Freilich2013), where, however, the integration (3.3) is performed numerically, in contrast to the analytical result below.
$z(\zeta )$. A similar construction is used to obtain the hollow vortex solutions in Crowdy & Green (Reference Crowdy and Green2011) and Crowdy et al. (Reference Crowdy, Llewellyn Smith and Freilich2013), where, however, the integration (3.3) is performed numerically, in contrast to the analytical result below.
3.1. Some special functions
We will perform our construction in terms of certain special functions, labelled here as ![]() $P(\zeta,q)$,
$P(\zeta,q)$, ![]() $K(\zeta,q)$ and
$K(\zeta,q)$ and ![]() $L(\zeta,q)$. We define these and state their relevant properties in this section. We refer the reader to Crowdy (Reference Crowdy2020) for further discussion of these functions, including their connection to more traditionally used elliptic functions (as used, for example, in Gurevitch Reference Gurevitch1965; Semenov & Wu Reference Semenov and Wu2020). The advantage of the functions that we use here is that their singularity and periodicity structures present themselves clearly, although it should be possible to derive similar properties for elliptic functions.
$L(\zeta,q)$. We define these and state their relevant properties in this section. We refer the reader to Crowdy (Reference Crowdy2020) for further discussion of these functions, including their connection to more traditionally used elliptic functions (as used, for example, in Gurevitch Reference Gurevitch1965; Semenov & Wu Reference Semenov and Wu2020). The advantage of the functions that we use here is that their singularity and periodicity structures present themselves clearly, although it should be possible to derive similar properties for elliptic functions.
To begin, we define the transformation ![]() $\theta _n(\zeta )=q^{2n}\zeta$ for all
$\theta _n(\zeta )=q^{2n}\zeta$ for all ![]() $n\in \mathbb {Z}$ (note that
$n\in \mathbb {Z}$ (note that ![]() $\theta _0(\zeta )=\zeta$ is the identity transformation), and the set
$\theta _0(\zeta )=\zeta$ is the identity transformation), and the set ![]() $\varTheta =\{\theta _n(\zeta )\mid n\in \mathbb {Z}\}$. Next, we introduce
$\varTheta =\{\theta _n(\zeta )\mid n\in \mathbb {Z}\}$. Next, we introduce ![]() $D_{\zeta }^{-1}$ to denote the reflection of
$D_{\zeta }^{-1}$ to denote the reflection of ![]() $D_{\zeta }$ in
$D_{\zeta }$ in ![]() $C_0$, where by reflection in
$C_0$, where by reflection in ![]() $C_0$ we mean the transformation
$C_0$ we mean the transformation ![]() $\zeta \mapsto 1/\bar {\zeta }$:
$\zeta \mapsto 1/\bar {\zeta }$: ![]() $D_{\zeta }^{-1}$ is the annular domain bounded by the circles
$D_{\zeta }^{-1}$ is the annular domain bounded by the circles ![]() $C_0$ and
$C_0$ and ![]() $C_{-1}$, where the latter denotes the reflection of
$C_{-1}$, where the latter denotes the reflection of ![]() $C_1$ in
$C_1$ in ![]() $C_0$ and is centred on the origin and of radius
$C_0$ and is centred on the origin and of radius ![]() $1/q$ (see figure 3). We define
$1/q$ (see figure 3). We define ![]() $F$ to be the region that consists of the union of
$F$ to be the region that consists of the union of ![]() $\overline {D_{\zeta }}$ and
$\overline {D_{\zeta }}$ and ![]() $D_{\zeta }^{-1}$, where we use the ‘overline’ notation with respect to a domain to denote the domain's closure, i.e.
$D_{\zeta }^{-1}$, where we use the ‘overline’ notation with respect to a domain to denote the domain's closure, i.e.
so ![]() $F$ does not contain
$F$ does not contain ![]() $C_{-1}$. The images of
$C_{-1}$. The images of ![]() $F$ under all elements of
$F$ under all elements of ![]() $\varTheta$ are mutually disjoint and cover the whole of the
$\varTheta$ are mutually disjoint and cover the whole of the ![]() $\zeta$-plane, except for the origin and the point at infinity.
$\zeta$-plane, except for the origin and the point at infinity. ![]() $\varTheta$ is in fact an example of a Schottky group (Ford Reference Ford1972; Crowdy Reference Crowdy2020). We refer to
$\varTheta$ is in fact an example of a Schottky group (Ford Reference Ford1972; Crowdy Reference Crowdy2020). We refer to ![]() $F$ as a fundamental region of
$F$ as a fundamental region of ![]() $\varTheta$. (The fundamental region of a Schottky group is not unique.)
$\varTheta$. (The fundamental region of a Schottky group is not unique.)

Figure 3. The annuli appearing in the analysis: ![]() $D_{\zeta }^{-1}$ (light grey) is the reflection of the pre-image domain
$D_{\zeta }^{-1}$ (light grey) is the reflection of the pre-image domain ![]() $D_{\zeta }$ (turquoise) of figure 2 in the unit circle
$D_{\zeta }$ (turquoise) of figure 2 in the unit circle ![]() $C_0$ (dotted blue). The union of
$C_0$ (dotted blue). The union of ![]() $\overline {D_{\zeta }}$ and
$\overline {D_{\zeta }}$ and ![]() $D_{\zeta }^{-1}$ forms the fundamental region
$D_{\zeta }^{-1}$ forms the fundamental region ![]() $F$ of (3.4) for the group
$F$ of (3.4) for the group ![]() $\varTheta$. The union of
$\varTheta$. The union of ![]() $\bar {F}$ and the reflection of
$\bar {F}$ and the reflection of ![]() $F$ (dark grey) in the circle
$F$ (dark grey) in the circle ![]() $C_1$ (dotted red) forms the fundamental region
$C_1$ (dotted red) forms the fundamental region ![]() $\hat {F}$ of (3.13) for the group
$\hat {F}$ of (3.13) for the group ![]() $\hat {\varTheta }$. The complex velocity
$\hat {\varTheta }$. The complex velocity ![]() $W'(\zeta )$ has double poles (blue crosses) at
$W'(\zeta )$ has double poles (blue crosses) at ![]() $\zeta =-\mathrm {i}$ and
$\zeta =-\mathrm {i}$ and ![]() $-\mathrm {i}q^2$, and simple zeros (blue circles) at
$-\mathrm {i}q^2$, and simple zeros (blue circles) at ![]() $\zeta =\zeta _2$,
$\zeta =\zeta _2$, ![]() $-\overline {\zeta _2}$,
$-\overline {\zeta _2}$, ![]() $1/\overline {\zeta _2}$ and
$1/\overline {\zeta _2}$ and ![]() $-1/\zeta _2$. The mapped complex velocity
$-1/\zeta _2$. The mapped complex velocity ![]() $\varOmega (\zeta )$ has simple poles (red crosses) at
$\varOmega (\zeta )$ has simple poles (red crosses) at ![]() $\zeta =\zeta _1$ and
$\zeta =\zeta _1$ and ![]() $-1/\zeta _2$ (coinciding with a zero of
$-1/\zeta _2$ (coinciding with a zero of ![]() $W'(\zeta )$), and simple zeros (red discs) at
$W'(\zeta )$), and simple zeros (red discs) at ![]() $\zeta =1/\overline {\zeta _1}$ and
$\zeta =1/\overline {\zeta _1}$ and ![]() $-\overline {\zeta _2}$ (also coinciding with a zero of
$-\overline {\zeta _2}$ (also coinciding with a zero of ![]() $W'(\zeta )$).
$W'(\zeta )$).
Now, the function ![]() $P(\zeta,q)$ is defined for all complex
$P(\zeta,q)$ is defined for all complex ![]() $\zeta$ and (real)
$\zeta$ and (real) ![]() $q$ with
$q$ with ![]() $0< q<1$, by
$0< q<1$, by
 \begin{equation} P(\zeta,q)=(1-\zeta)\prod_{n=1}^{\infty}(1-q^{2n}\zeta)(1-q^{2n}\zeta^{{-}1}). \end{equation}
\begin{equation} P(\zeta,q)=(1-\zeta)\prod_{n=1}^{\infty}(1-q^{2n}\zeta)(1-q^{2n}\zeta^{{-}1}). \end{equation}
Up to a normalisation, ![]() $P(\zeta,q)$ is the Schottky–Klein prime function associated with
$P(\zeta,q)$ is the Schottky–Klein prime function associated with ![]() $\varTheta$. One can check that
$\varTheta$. One can check that ![]() $P(\zeta,q)$ is analytic everywhere in
$P(\zeta,q)$ is analytic everywhere in ![]() $F$, and is non-zero in
$F$, and is non-zero in ![]() $F$ except for a simple zero at
$F$ except for a simple zero at ![]() $\zeta =1$. Furthermore, one can deduce directly from (3.5) that
$\zeta =1$. Furthermore, one can deduce directly from (3.5) that
Relation (3.6a) can be used to continue ![]() $P(\zeta,q)$ to points
$P(\zeta,q)$ to points ![]() $\zeta$ outside of
$\zeta$ outside of ![]() $F$. In particular, one can deduce from (3.6a), and the properties of
$F$. In particular, one can deduce from (3.6a), and the properties of ![]() $P(\zeta,q)$ for
$P(\zeta,q)$ for ![]() $\zeta \in F$ noted above, that
$\zeta \in F$ noted above, that ![]() $P(\zeta,q)$ is analytic everywhere in the
$P(\zeta,q)$ is analytic everywhere in the ![]() $\zeta$-plane except for essential singularities at the origin and the point at infinity, and that it has simple zeros at
$\zeta$-plane except for essential singularities at the origin and the point at infinity, and that it has simple zeros at ![]() $\zeta =q^{2n}$ for all
$\zeta =q^{2n}$ for all ![]() $n\in \mathbb {Z}$. Of course, one could also deduce these properties directly from (3.5).
$n\in \mathbb {Z}$. Of course, one could also deduce these properties directly from (3.5).
Next, the function ![]() $K(\zeta,q)$ is defined by
$K(\zeta,q)$ is defined by
It follows from (3.5) that
 \begin{equation} K(\zeta,q)= \frac{1}{\zeta-1}+1 +\sum_{n=1}^{\infty} q^{2n} \left( \frac{1}{\zeta-q^{2n}} -\frac{1}{\zeta^{{-}1}-q^{2n}} \right). \end{equation}
\begin{equation} K(\zeta,q)= \frac{1}{\zeta-1}+1 +\sum_{n=1}^{\infty} q^{2n} \left( \frac{1}{\zeta-q^{2n}} -\frac{1}{\zeta^{{-}1}-q^{2n}} \right). \end{equation}
One may check that ![]() $K(\zeta,q)$ is analytic everywhere in
$K(\zeta,q)$ is analytic everywhere in ![]() $F$ except for a simple pole at
$F$ except for a simple pole at ![]() $\zeta =1$ with residue
$\zeta =1$ with residue ![]() $1$. Also, it follows from (3.6) that
$1$. Also, it follows from (3.6) that
Finally, the function ![]() $L(\zeta,q)$ is defined by
$L(\zeta,q)$ is defined by
It follows from (3.8) that
 \begin{equation} L(\zeta,q)= \frac{-1}{(\zeta-1)^2} -\frac{1}{\zeta-1} -\zeta\sum_{n=1}^{\infty} q^{2n} \left( \frac{1}{(\zeta-q^{2n})^2} +\frac{1}{(1-q^{2n}\zeta)^2} \right). \end{equation}
\begin{equation} L(\zeta,q)= \frac{-1}{(\zeta-1)^2} -\frac{1}{\zeta-1} -\zeta\sum_{n=1}^{\infty} q^{2n} \left( \frac{1}{(\zeta-q^{2n})^2} +\frac{1}{(1-q^{2n}\zeta)^2} \right). \end{equation}
One may check that ![]() $L(\zeta,q)$ is analytic everywhere in
$L(\zeta,q)$ is analytic everywhere in ![]() $F$ except for a double pole at
$F$ except for a double pole at ![]() $\zeta =1$ with residue
$\zeta =1$ with residue ![]() $-1$. Also, it follows from (3.9) that
$-1$. Also, it follows from (3.9) that
In addition to the above, we will also make use of the functions ![]() $P(\zeta,q^2)$,
$P(\zeta,q^2)$, ![]() $K(\zeta,q^2)$ and
$K(\zeta,q^2)$ and ![]() $L(\zeta,q^2)$. Of course, with
$L(\zeta,q^2)$. Of course, with ![]() $0< q<1$, we also have
$0< q<1$, we also have ![]() $0< q^2<1$, so
$0< q^2<1$, so ![]() $P(\zeta,q^2)$ is defined by (3.5) simply with
$P(\zeta,q^2)$ is defined by (3.5) simply with ![]() $q$ replaced by
$q$ replaced by ![]() $q^2$. And
$q^2$. And ![]() $P(\zeta,q^2)$ is (up to a normalisation) the Schottky–Klein prime function associated with
$P(\zeta,q^2)$ is (up to a normalisation) the Schottky–Klein prime function associated with ![]() $\hat {\varTheta }=\{\theta _{2n}(\zeta )\mid n\in \mathbb {Z}\}$, which is a subgroup of
$\hat {\varTheta }=\{\theta _{2n}(\zeta )\mid n\in \mathbb {Z}\}$, which is a subgroup of ![]() $\varTheta$ and itself a Schottky group (Vasconcelos, Marshall & Crowdy Reference Vasconcelos, Marshall and Crowdy2015). A fundamental region of
$\varTheta$ and itself a Schottky group (Vasconcelos, Marshall & Crowdy Reference Vasconcelos, Marshall and Crowdy2015). A fundamental region of ![]() $\hat {\varTheta }$ is
$\hat {\varTheta }$ is
i.e. the region that consists of the union of ![]() $\bar {F}$ and the reflection of
$\bar {F}$ and the reflection of ![]() $F$ in the circle
$F$ in the circle ![]() $C_1$, where reflection in
$C_1$, where reflection in ![]() $C_1$ is given by
$C_1$ is given by ![]() $\zeta \mapsto q^2/\bar {\zeta }$ (see figure 3).
$\zeta \mapsto q^2/\bar {\zeta }$ (see figure 3).
It follows directly from (3.5) that
and hence from (3.7) and (3.10) that
3.2. Constructing the complex potential  $W(\zeta )=w(z)$
$W(\zeta )=w(z)$
The construction of ![]() $W(\zeta )$ is straightforward as it is simply the complex potential for flow in the annulus
$W(\zeta )$ is straightforward as it is simply the complex potential for flow in the annulus ![]() $D_{\zeta }$, driven by a dipole at
$D_{\zeta }$, driven by a dipole at ![]() $-\mathrm {i}$ and having circulation
$-\mathrm {i}$ and having circulation ![]() $\varGamma$ around
$\varGamma$ around ![]() $C_1$ with stagnation points at
$C_1$ with stagnation points at ![]() $\zeta _2$ and
$\zeta _2$ and ![]() $\zeta _3$. Since both
$\zeta _3$. Since both ![]() $D_{\zeta }$ and the dipole flow are right–left symmetric,
$D_{\zeta }$ and the dipole flow are right–left symmetric, ![]() $\zeta _3=-\overline {\zeta _2}$, as shown in § 3.2.1 below. Figure 4(a) shows contours of
$\zeta _3=-\overline {\zeta _2}$, as shown in § 3.2.1 below. Figure 4(a) shows contours of ![]() $\mathrm {Im}\{W(\zeta )\}$ – i.e. flow streamlines – in
$\mathrm {Im}\{W(\zeta )\}$ – i.e. flow streamlines – in ![]() $D_{\zeta }$ for a typical solution.
$D_{\zeta }$ for a typical solution.

Figure 4. Illustrations of the solution components for a typical solution (namely, that which is illustrated in figure 6(b) below). Here, ![]() $\alpha =-{\rm \pi} /4$ and
$\alpha =-{\rm \pi} /4$ and ![]() $y_c=0.3$ (see (3.51)). (a) Contours of
$y_c=0.3$ (see (3.51)). (a) Contours of ![]() $\mathrm {Im}\{W(\zeta )\}$ as given by (3.19), giving the flow streamlines in the pre-image domain
$\mathrm {Im}\{W(\zeta )\}$ as given by (3.19), giving the flow streamlines in the pre-image domain ![]() $D_{\zeta }$ with a dipole at
$D_{\zeta }$ with a dipole at ![]() $\zeta =\mathrm {-i}$ (which corresponds to the point at infinity in
$\zeta =\mathrm {-i}$ (which corresponds to the point at infinity in ![]() $D$), stagnation points symmetrically at
$D$), stagnation points symmetrically at ![]() $\zeta =\zeta _2$ (the trailing edge in
$\zeta =\zeta _2$ (the trailing edge in ![]() $D$) and
$D$) and ![]() $-\overline {\zeta _2}$ (on the leading face in
$-\overline {\zeta _2}$ (on the leading face in ![]() $D$), and tangential flow along
$D$), and tangential flow along ![]() $C_0$ (the free surface in
$C_0$ (the free surface in ![]() $D$) and
$D$) and ![]() $C_1$ (the foil). (b) Isotachs, contours of
$C_1$ (the foil). (b) Isotachs, contours of ![]() $|\varOmega (\zeta )|$ as given by (3.34), the flow speed mapped to the pre-image domain
$|\varOmega (\zeta )|$ as given by (3.34), the flow speed mapped to the pre-image domain ![]() $D_{\zeta }$, with infinite speed at
$D_{\zeta }$, with infinite speed at ![]() $\zeta _1$ (the leading edge in
$\zeta _1$ (the leading edge in ![]() $D$), a single stagnation point at
$D$), a single stagnation point at ![]() $\zeta =-\overline {\zeta _2}$ (on the leading face in
$\zeta =-\overline {\zeta _2}$ (on the leading face in ![]() $D$), and constant speed along
$D$), and constant speed along ![]() $C_0$ (the free surface in
$C_0$ (the free surface in ![]() $D$), with no stagnation point at
$D$), with no stagnation point at ![]() $\zeta =\zeta _2$ (the trailing edge in
$\zeta =\zeta _2$ (the trailing edge in ![]() $D$) where the speed is finite.
$D$) where the speed is finite.
It follows from the properties of ![]() $w(z)$ and
$w(z)$ and ![]() $z(\zeta )$ noted above that
$z(\zeta )$ noted above that ![]() $W(\zeta )$ must be analytic for all
$W(\zeta )$ must be analytic for all ![]() $\zeta \in D_{\zeta }$ except that (as follows from (2.1) and (3.1)) for
$\zeta \in D_{\zeta }$ except that (as follows from (2.1) and (3.1)) for ![]() $\zeta$ local to
$\zeta$ local to ![]() $-\mathrm {i}$, to leading order,
$-\mathrm {i}$, to leading order,
Also, it follows from (2.2) that
Furthermore, it follows from (2.6) that
where we can take ![]() $\hat {\mathcal {C}}$ to be a circle centred on the origin, of some radius
$\hat {\mathcal {C}}$ to be a circle centred on the origin, of some radius ![]() $\hat {q}$, where
$\hat {q}$, where ![]() $q<\hat {q}<1$ (so that
$q<\hat {q}<1$ (so that ![]() $\hat {\mathcal {C}}$ lies in the interior of
$\hat {\mathcal {C}}$ lies in the interior of ![]() $D_{\zeta }$), and we integrate around
$D_{\zeta }$), and we integrate around ![]() $\hat {\mathcal {C}}$ in the anticlockwise direction. Recall that
$\hat {\mathcal {C}}$ in the anticlockwise direction. Recall that ![]() $\varGamma$ is still to be determined. We propose that
$\varGamma$ is still to be determined. We propose that
One can verify that ![]() $W(\zeta )$ as stated by (3.19) possesses the properties stated above, as follows. First, it follows from the properties of
$W(\zeta )$ as stated by (3.19) possesses the properties stated above, as follows. First, it follows from the properties of ![]() $K(\zeta,q)$, that
$K(\zeta,q)$, that ![]() $W(\zeta )$ as given by (3.19) is analytic for all
$W(\zeta )$ as given by (3.19) is analytic for all ![]() $\zeta \in D_{\zeta }$ except for a simple pole with residue
$\zeta \in D_{\zeta }$ except for a simple pole with residue ![]() $Ua$ at
$Ua$ at ![]() $\zeta =-\mathrm {i}$, as required by (3.16). It is also evident that this form for
$\zeta =-\mathrm {i}$, as required by (3.16). It is also evident that this form for ![]() $W(\zeta )$ satisfies (3.18). Finally, to check the boundary conditions (3.17), it is helpful to first note that
$W(\zeta )$ satisfies (3.18). Finally, to check the boundary conditions (3.17), it is helpful to first note that
where the first equality follows from the fact that for ![]() $\zeta \in C_0$,
$\zeta \in C_0$, ![]() $\bar {\zeta }=1/\zeta$, and the second follows from (3.9b). Similarly,
$\bar {\zeta }=1/\zeta$, and the second follows from (3.9b). Similarly,
where now the first equality follows from the fact that for ![]() $\zeta \in C_1$,
$\zeta \in C_1$, ![]() $\bar {\zeta }=q^2/\zeta$, and the second follows by using both equations in (3.9). Then one may deduce that (3.17) holds (with
$\bar {\zeta }=q^2/\zeta$, and the second follows by using both equations in (3.9). Then one may deduce that (3.17) holds (with ![]() $\psi _0=Ua/2$ and
$\psi _0=Ua/2$ and ![]() $\psi _1=-(\varGamma /(2{\rm \pi} ))\ln q$). This completes our verification of (3.19). Similar arguments to those below for
$\psi _1=-(\varGamma /(2{\rm \pi} ))\ln q$). This completes our verification of (3.19). Similar arguments to those below for ![]() $\varOmega (\zeta )$ show that
$\varOmega (\zeta )$ show that ![]() $W(\zeta )$ is unique.
$W(\zeta )$ is unique.
Differentiating (3.19) gives
Now, in order to impose the Kutta condition at the trailing endpoint ![]() $z_2$ of the hydrofoil, we must choose
$z_2$ of the hydrofoil, we must choose ![]() $\varGamma$ such that
$\varGamma$ such that ![]() $W'(\zeta _2)=0$, giving
$W'(\zeta _2)=0$, giving
(Note that it follows from (3.24) that ![]() $L(\mathrm {i}\zeta _2,q)$ is real.)
$L(\mathrm {i}\zeta _2,q)$ is real.)
3.2.1. Properties of  $W'(\zeta )$, the complex velocity in
$W'(\zeta )$, the complex velocity in  $D_\zeta$
$D_\zeta$
We now note some properties of ![]() $W'(\zeta )$ that will be useful later. First,
$W'(\zeta )$ that will be useful later. First, ![]() $W'(-\overline {\zeta _2})=0$. This follows from (3.22) using the fact that
$W'(-\overline {\zeta _2})=0$. This follows from (3.22) using the fact that ![]() $W'(\zeta _2)=0$ and
$W'(\zeta _2)=0$ and
where the second equality follows by using both equations in (3.12). We will henceforth assume that ![]() $-\overline {\zeta _2}\neq \zeta _2$, or equivalently, that
$-\overline {\zeta _2}\neq \zeta _2$, or equivalently, that ![]() $\zeta _2\neq \pm \mathrm {i}q$ (although, in § 5.2, we will consider the limit of our results as
$\zeta _2\neq \pm \mathrm {i}q$ (although, in § 5.2, we will consider the limit of our results as ![]() $\zeta _2\rightarrow \pm \mathrm {i}q$, whilst
$\zeta _2\rightarrow \pm \mathrm {i}q$, whilst ![]() $\zeta _1\rightarrow \mp \mathrm {i}q$, respectively). We now claim that the zeros of
$\zeta _1\rightarrow \mp \mathrm {i}q$, respectively). We now claim that the zeros of ![]() $W'(\zeta )$ at
$W'(\zeta )$ at ![]() $\zeta =\zeta _2$ and
$\zeta =\zeta _2$ and ![]() $-\overline {\zeta _2}$ are the only zeros of
$-\overline {\zeta _2}$ are the only zeros of ![]() $W'(\zeta )$ in
$W'(\zeta )$ in ![]() $F$, and are simple zeros. To demonstrate this, note that it follows from (3.22) and (3.12a) that
$F$, and are simple zeros. To demonstrate this, note that it follows from (3.22) and (3.12a) that
Thus
It then follows from (3.26) and an application of the argument principle (Ahlfors Reference Ahlfors1979, § 5.2) that ![]() $W'(\zeta )$ has the same number of poles as zeros in
$W'(\zeta )$ has the same number of poles as zeros in ![]() $F$, where these are both counted according to their multiplicities. (Here,
$F$, where these are both counted according to their multiplicities. (Here, ![]() $\zeta _2$ and
$\zeta _2$ and ![]() $-\overline {\zeta _2}$ lie on the boundary of
$-\overline {\zeta _2}$ lie on the boundary of ![]() $F$, but by standard arguments one can adapt the argument principle to take account of this.) But it follows from (3.22) and the properties of
$F$, but by standard arguments one can adapt the argument principle to take account of this.) But it follows from (3.22) and the properties of ![]() $L(\zeta,q)$ that
$L(\zeta,q)$ that ![]() $W'(\zeta )$ has a double pole at
$W'(\zeta )$ has a double pole at ![]() $\zeta =-\mathrm {i}$ and no other singularities in
$\zeta =-\mathrm {i}$ and no other singularities in ![]() $F$. Thus, as claimed, the zeros of
$F$. Thus, as claimed, the zeros of ![]() $W'(\zeta )$ at
$W'(\zeta )$ at ![]() $\zeta =\zeta _2$ and
$\zeta =\zeta _2$ and ![]() $-\overline {\zeta _2}$ must be the only zeros of
$-\overline {\zeta _2}$ must be the only zeros of ![]() $W'(\zeta )$ in
$W'(\zeta )$ in ![]() $F$, and must be simple zeros. It also then follows that
$F$, and must be simple zeros. It also then follows that
Finally, one may also deduce that ![]() $W'(\zeta )$ is analytic for all
$W'(\zeta )$ is analytic for all ![]() $\zeta \in \hat {F}$ except for double poles at
$\zeta \in \hat {F}$ except for double poles at ![]() $\zeta =-\mathrm {i}$ and
$\zeta =-\mathrm {i}$ and ![]() $-\mathrm {i}q^2$, and that the only zeros of
$-\mathrm {i}q^2$, and that the only zeros of ![]() $W'(\zeta )$ in
$W'(\zeta )$ in ![]() $\hat {F}$ are simple zeros at
$\hat {F}$ are simple zeros at ![]() $\zeta =\zeta _2$,
$\zeta =\zeta _2$, ![]() $-\overline {\zeta _2}$,
$-\overline {\zeta _2}$, ![]() $1/\overline {\zeta _2}$ and
$1/\overline {\zeta _2}$ and ![]() $-1/\zeta _2$ – see figure 3. (
$-1/\zeta _2$ – see figure 3. (![]() $W'(\zeta )$ also has zeros at
$W'(\zeta )$ also has zeros at ![]() $\zeta =q^2\zeta _2$ and
$\zeta =q^2\zeta _2$ and ![]() $-q^2\overline {\zeta _2}$, but both of these points have modulus
$-q^2\overline {\zeta _2}$, but both of these points have modulus ![]() $q^3$ and so are not contained in
$q^3$ and so are not contained in ![]() $\hat {F}$.)
$\hat {F}$.)
3.3. Constructing the mapped complex velocity  $\varOmega (\zeta )=w'(z)$
$\varOmega (\zeta )=w'(z)$
It follows from the properties of ![]() $w'(z)$ and
$w'(z)$ and ![]() $z(\zeta )$ stated above that
$z(\zeta )$ stated above that ![]() $\varOmega (\zeta )$ must be analytic for all
$\varOmega (\zeta )$ must be analytic for all ![]() $\zeta \in D_{\zeta }$ except for a simple pole at
$\zeta \in D_{\zeta }$ except for a simple pole at ![]() $\zeta =\zeta _1$ (as follows from (2.5) and the fact that
$\zeta =\zeta _1$ (as follows from (2.5) and the fact that ![]() $z'(\zeta )$ has a simple zero at
$z'(\zeta )$ has a simple zero at ![]() $\zeta _1$). Furthermore,
$\zeta _1$). Furthermore, ![]() $\varOmega (\zeta )$ must be non-zero for all
$\varOmega (\zeta )$ must be non-zero for all ![]() $\zeta$ in the closure of
$\zeta$ in the closure of ![]() $D_{\zeta }$ except for a simple zero at
$D_{\zeta }$ except for a simple zero at ![]() $\zeta =-\overline {\zeta _2}$ (as follows from (2.7), recalling (3.27)). Note that
$\zeta =-\overline {\zeta _2}$ (as follows from (2.7), recalling (3.27)). Note that ![]() $\varOmega (\zeta )$ is non-zero at
$\varOmega (\zeta )$ is non-zero at ![]() $\zeta =\zeta _2$ – i.e.
$\zeta =\zeta _2$ – i.e. ![]() $w'(z)$ is non-zero at the trailing endpoint
$w'(z)$ is non-zero at the trailing endpoint ![]() $z_2$ of the hydrofoil – because
$z_2$ of the hydrofoil – because ![]() $W'(\zeta )$ and
$W'(\zeta )$ and ![]() $z'(\zeta )$ both have simple zeros at
$z'(\zeta )$ both have simple zeros at ![]() $\zeta =\zeta _2$ (and
$\zeta =\zeta _2$ (and ![]() $\varOmega (\zeta )=W'(\zeta )/z'(\zeta )$). In addition, it follows from (2.3) and (2.4) that
$\varOmega (\zeta )=W'(\zeta )/z'(\zeta )$). In addition, it follows from (2.3) and (2.4) that
and from (2.1) that
Figure 4(b) illustrates the mapped flow speed ![]() $|\varOmega (\zeta )|$ in
$|\varOmega (\zeta )|$ in ![]() $D_{\zeta }$ for a typical solution.
$D_{\zeta }$ for a typical solution.
It follows from (3.28a) that for ![]() $\zeta \in C_0$, since
$\zeta \in C_0$, since ![]() $\bar {\zeta }=1/\zeta$,
$\bar {\zeta }=1/\zeta$,
where we define ![]() $\bar {\varOmega }(\zeta )=\overline {\varOmega (\bar {\zeta })}$. However, it follows from the properties of
$\bar {\varOmega }(\zeta )=\overline {\varOmega (\bar {\zeta })}$. However, it follows from the properties of ![]() $\varOmega (\zeta )$ that
$\varOmega (\zeta )$ that ![]() $1/\bar {\varOmega }(1/\zeta )$ is analytic for all
$1/\bar {\varOmega }(1/\zeta )$ is analytic for all ![]() $\zeta \in D_{\zeta }^{-1}$ except for a simple pole at
$\zeta \in D_{\zeta }^{-1}$ except for a simple pole at ![]() $\zeta =-1/\zeta _2$, and also non-zero for all
$\zeta =-1/\zeta _2$, and also non-zero for all ![]() $\zeta$ in the closure of
$\zeta$ in the closure of ![]() $D_{\zeta }^{-1}$ except for a simple zero at
$D_{\zeta }^{-1}$ except for a simple zero at ![]() $\zeta =1/\overline {\zeta _1}$. It then follows by analytic continuation that (3.30) must in fact hold for all
$\zeta =1/\overline {\zeta _1}$. It then follows by analytic continuation that (3.30) must in fact hold for all ![]() $\zeta$ in the closure of
$\zeta$ in the closure of ![]() $F$, and that
$F$, and that ![]() $\varOmega (\zeta )$ is analytic for all
$\varOmega (\zeta )$ is analytic for all ![]() $\zeta \in F$ except for simple poles at
$\zeta \in F$ except for simple poles at ![]() $\zeta =\zeta _1$ and
$\zeta =\zeta _1$ and ![]() $-1/\zeta _2$. Furthermore, the only zeros of
$-1/\zeta _2$. Furthermore, the only zeros of ![]() $\varOmega (\zeta )$ in
$\varOmega (\zeta )$ in ![]() $F$ are simple zeros at
$F$ are simple zeros at ![]() $\zeta =-\overline {\zeta _2}$ and
$\zeta =-\overline {\zeta _2}$ and ![]() $1/\overline {\zeta _1}$.
$1/\overline {\zeta _1}$.
Next, one may deduce from (3.28b) that for ![]() $\zeta \in C_1$, since
$\zeta \in C_1$, since ![]() $\bar {\zeta }=q^2/\zeta$,
$\bar {\zeta }=q^2/\zeta$,
Then, by arguments similar to those just stated after (3.30), it follows that (3.31) must in fact hold for all ![]() $\zeta$ in the closure of
$\zeta$ in the closure of ![]() $\hat {F}$. But furthermore, one may deduce that
$\hat {F}$. But furthermore, one may deduce that ![]() $\varOmega (\zeta )$ is analytic for all
$\varOmega (\zeta )$ is analytic for all ![]() $\zeta \in \hat {F}$ except for simple poles at
$\zeta \in \hat {F}$ except for simple poles at ![]() $\zeta =\zeta _1$ and
$\zeta =\zeta _1$ and ![]() $-1/\zeta _2$, and that the only zeros of
$-1/\zeta _2$, and that the only zeros of ![]() $\varOmega (\zeta )$ in
$\varOmega (\zeta )$ in ![]() $\hat {F}$ are simple zeros at
$\hat {F}$ are simple zeros at ![]() $\zeta =-\overline {\zeta _2}$ and
$\zeta =-\overline {\zeta _2}$ and ![]() $1/\overline {\zeta _1}$ – see figure 3.
$1/\overline {\zeta _1}$ – see figure 3.
Now note that by repeated analytic continuation, one may show that (3.30) and (3.31) in fact hold for all ![]() $\zeta$, except at
$\zeta$, except at ![]() $0$ and infinity. Combining these two relations gives
$0$ and infinity. Combining these two relations gives
hence
from which one may deduce that ![]() $\varOmega (\zeta )$ is automorphic with respect to the group
$\varOmega (\zeta )$ is automorphic with respect to the group ![]() $\hat {\varTheta }$. The property (3.33), together with the properties of
$\hat {\varTheta }$. The property (3.33), together with the properties of ![]() $\varOmega (\zeta )$ for
$\varOmega (\zeta )$ for ![]() $\zeta$ in the fundamental region
$\zeta$ in the fundamental region ![]() $\hat {F}$ of
$\hat {F}$ of ![]() $\hat {\varTheta }$ that are stated just after (3.31), along with the normalisation (3.29), are enough to identify
$\hat {\varTheta }$ that are stated just after (3.31), along with the normalisation (3.29), are enough to identify ![]() $\varOmega (\zeta )$ uniquely. To check this, consider the ratio of
$\varOmega (\zeta )$ uniquely. To check this, consider the ratio of ![]() $\varOmega (\zeta )$ and any other function that has these properties. This ratio must be analytic everywhere in
$\varOmega (\zeta )$ and any other function that has these properties. This ratio must be analytic everywhere in ![]() $\hat {F}$ (all poles of the numerator are cancelled by the same poles of the denominator; likewise all zeros of the denominator are cancelled by the same zeros of the numerator), and also automorphic with respect to
$\hat {F}$ (all poles of the numerator are cancelled by the same poles of the denominator; likewise all zeros of the denominator are cancelled by the same zeros of the numerator), and also automorphic with respect to ![]() $\hat {\varTheta }$. It then follows from the extended form of Liouville's theorem for automorphic functions (e.g. see Ford Reference Ford1972), that this ratio must equal a constant. But it follows from the normalisation on
$\hat {\varTheta }$. It then follows from the extended form of Liouville's theorem for automorphic functions (e.g. see Ford Reference Ford1972), that this ratio must equal a constant. But it follows from the normalisation on ![]() $\varOmega (\zeta )$ that is imposed by (3.29) that this constant must equal
$\varOmega (\zeta )$ that is imposed by (3.29) that this constant must equal ![]() $1$. We thus seek to construct a function with these properties. One could construct this as a ratio of products of
$1$. We thus seek to construct a function with these properties. One could construct this as a ratio of products of ![]() $P$ functions. However, it will be more convenient later – in particular, we will wish to differentiate
$P$ functions. However, it will be more convenient later – in particular, we will wish to differentiate ![]() $\varOmega (\zeta )$ (with respect to
$\varOmega (\zeta )$ (with respect to ![]() $\zeta$) – to instead construct it as a sum of the form
$\zeta$) – to instead construct it as a sum of the form
for some (unique) constants ![]() $\alpha _0$,
$\alpha _0$, ![]() $\alpha _1$ and
$\alpha _1$ and ![]() $\alpha _2$, which we will determine in due course. We highlight the fact that the second argument of the
$\alpha _2$, which we will determine in due course. We highlight the fact that the second argument of the ![]() $K$ functions that appear in (3.34) is
$K$ functions that appear in (3.34) is ![]() $q^2$, not
$q^2$, not ![]() $q$.
$q$.
One may verify (3.34) as follows. First, one may check from the properties of ![]() $K(\zeta,q)$ that for all values of
$K(\zeta,q)$ that for all values of ![]() $\alpha _0$,
$\alpha _0$, ![]() $\alpha _1$ and
$\alpha _1$ and ![]() $\alpha _2$, the function on the right-hand side of (3.34) is analytic for all
$\alpha _2$, the function on the right-hand side of (3.34) is analytic for all ![]() $\zeta \in \hat {F}$ except for simple poles at
$\zeta \in \hat {F}$ except for simple poles at ![]() $\zeta =\zeta _1$ and
$\zeta =\zeta _1$ and ![]() $-1/\zeta _2$, as required. However, in order for it to satisfy (3.33), it follows from (3.9a) that
$-1/\zeta _2$, as required. However, in order for it to satisfy (3.33), it follows from (3.9a) that
Next, in order that ![]() $\varOmega (-\overline {\zeta _2})=0$, it follows – using the fact that
$\varOmega (-\overline {\zeta _2})=0$, it follows – using the fact that ![]() $K(q^2,q^2)=0$ (which one may deduce by using both equations in (3.9) to show that
$K(q^2,q^2)=0$ (which one may deduce by using both equations in (3.9) to show that ![]() $K(q^2,q^2)=-K(q^2,q^2)$) – that also
$K(q^2,q^2)=-K(q^2,q^2)$) – that also
Note that we will assume that ![]() $\zeta _1\neq -\overline {\zeta _2}$, as otherwise
$\zeta _1\neq -\overline {\zeta _2}$, as otherwise ![]() $K(-\overline {\zeta _2}/\zeta _1,q^2)$ is unbounded and – as will be shown in § 5.1 – the hydrofoil is horizontal.
$K(-\overline {\zeta _2}/\zeta _1,q^2)$ is unbounded and – as will be shown in § 5.1 – the hydrofoil is horizontal.
Next, one could also write down a relation between ![]() $\alpha _0$,
$\alpha _0$, ![]() $\alpha _1$ and
$\alpha _1$ and ![]() $\alpha _2$ by imposing on (3.34) the condition that
$\alpha _2$ by imposing on (3.34) the condition that ![]() $\varOmega (1/\overline {\zeta _1})=0$. However, one can show that this relation can be retrieved from (3.35) and (3.36) (using the fact that
$\varOmega (1/\overline {\zeta _1})=0$. However, one can show that this relation can be retrieved from (3.35) and (3.36) (using the fact that ![]() $\mathrm {Re}\{K(\zeta,q^2)\}=1/2$ for all
$\mathrm {Re}\{K(\zeta,q^2)\}=1/2$ for all ![]() $\zeta \in C_0$ – cf. (3.20)). Finally, then, it follows from (3.29) that
$\zeta \in C_0$ – cf. (3.20)). Finally, then, it follows from (3.29) that
Combining (3.35)–(3.37), and also making use of (3.9b), one arrives at
This also completes our check on (3.34).
3.4. Completing the solution: constructing the mapping  $z(\zeta )$
$z(\zeta )$
We now introduce the function
which may be determined as follows. First, it follows from (3.3) that
Then it follows from (3.25) and (3.33) that
Hence ![]() $H(\zeta )$ is automorphic with respect to
$H(\zeta )$ is automorphic with respect to ![]() $\hat {\varTheta }$. Furthermore, one can check from the properties of
$\hat {\varTheta }$. Furthermore, one can check from the properties of ![]() $W'(\zeta )$ and
$W'(\zeta )$ and ![]() $\varOmega (\zeta )$ identified in §§ 3.2 and 3.3 that
$\varOmega (\zeta )$ identified in §§ 3.2 and 3.3 that ![]() $H(\zeta )$ is analytic everywhere in
$H(\zeta )$ is analytic everywhere in ![]() $\hat {F}$ except for a simple pole at
$\hat {F}$ except for a simple pole at ![]() $\zeta =1/\overline {\zeta _1}$ and double poles at
$\zeta =1/\overline {\zeta _1}$ and double poles at ![]() $\zeta =-\mathrm {i}$ and
$\zeta =-\mathrm {i}$ and ![]() $-\mathrm {i}q^2$. These properties of
$-\mathrm {i}q^2$. These properties of ![]() $H(\zeta )$, along with its residues at the aforementioned poles and the coefficients of
$H(\zeta )$, along with its residues at the aforementioned poles and the coefficients of ![]() $(\zeta +\mathrm {i})^{-2}$ and
$(\zeta +\mathrm {i})^{-2}$ and ![]() $(\zeta +\mathrm {i}q^2)^{-2}$ in the Laurent series expansions of it about
$(\zeta +\mathrm {i}q^2)^{-2}$ in the Laurent series expansions of it about ![]() $\zeta =-\mathrm {i}$ and
$\zeta =-\mathrm {i}$ and ![]() $-\mathrm {i}q^2$, respectively, identify
$-\mathrm {i}q^2$, respectively, identify ![]() $H(\zeta )$ uniquely, up to an additive constant. This follows by arguments similar to those that we have already applied to
$H(\zeta )$ uniquely, up to an additive constant. This follows by arguments similar to those that we have already applied to ![]() $\varOmega (\zeta )$ (see the paragraph just after (3.33)), although one should now consider the difference of
$\varOmega (\zeta )$ (see the paragraph just after (3.33)), although one should now consider the difference of ![]() $H(\zeta )$ and any other function with these properties; this difference must be analytic everywhere in
$H(\zeta )$ and any other function with these properties; this difference must be analytic everywhere in ![]() $\hat {F}$, and automorphic with respect to
$\hat {F}$, and automorphic with respect to ![]() $\hat {\varTheta }$, and so must equal a constant. It then follows from the properties of
$\hat {\varTheta }$, and so must equal a constant. It then follows from the properties of ![]() $K(\zeta,q)$ and
$K(\zeta,q)$ and ![]() $L(\zeta,q)$ that we can write
$L(\zeta,q)$ that we can write
 \begin{align} H(\zeta)={}&\beta_1\,K(\overline{\zeta_1}\zeta,q^2) +\beta_2\,K(\mathrm{i}\zeta,q^2) +\beta_3\,K(\mathrm{i}q^2\zeta,q^2)\nonumber\\ &{}+\beta_4\,L(\mathrm{i}\zeta,q^2) +\beta_5\,L(\mathrm{i}q^2\zeta,q^2) +\beta_0, \end{align}
\begin{align} H(\zeta)={}&\beta_1\,K(\overline{\zeta_1}\zeta,q^2) +\beta_2\,K(\mathrm{i}\zeta,q^2) +\beta_3\,K(\mathrm{i}q^2\zeta,q^2)\nonumber\\ &{}+\beta_4\,L(\mathrm{i}\zeta,q^2) +\beta_5\,L(\mathrm{i}q^2\zeta,q^2) +\beta_0, \end{align}
for some unique constants ![]() $\beta _0,\ldots,\beta _5$. We determine these constants in Appendix A.
$\beta _0,\ldots,\beta _5$. We determine these constants in Appendix A.
Now note that, evidently, as follows from (3.39), dividing the right-hand side of (3.42) by ![]() $\zeta$ provides an expression for
$\zeta$ provides an expression for ![]() $z'(\zeta )$. Recalling (3.7) and (3.10), it is straightforward to integrate this expression to find
$z'(\zeta )$. Recalling (3.7) and (3.10), it is straightforward to integrate this expression to find
 \begin{align} z(\zeta)={}&\beta_1 \log P(\overline{\zeta_1}\zeta,q^2) +\beta_2 \log P(\mathrm{i}\zeta,q^2) +\beta_3 \log P(\mathrm{i}q^2\zeta,q^2)\nonumber\\ &{}+\beta_4\,K(\mathrm{i}\zeta,q^2) +\beta_5\,K(\mathrm{i}q^2\zeta,q^2) +c, \end{align}
\begin{align} z(\zeta)={}&\beta_1 \log P(\overline{\zeta_1}\zeta,q^2) +\beta_2 \log P(\mathrm{i}\zeta,q^2) +\beta_3 \log P(\mathrm{i}q^2\zeta,q^2)\nonumber\\ &{}+\beta_4\,K(\mathrm{i}\zeta,q^2) +\beta_5\,K(\mathrm{i}q^2\zeta,q^2) +c, \end{align}
where ![]() $c$ is an additional constant. One might expect to see the term
$c$ is an additional constant. One might expect to see the term ![]() $\beta _0\log \zeta$ on the right-hand side of (3.43). However, we can omit this for the following reason. Of course, our map
$\beta _0\log \zeta$ on the right-hand side of (3.43). However, we can omit this for the following reason. Of course, our map ![]() $z(\zeta )$ must be single-valued in
$z(\zeta )$ must be single-valued in ![]() $D_{\zeta }$; one can check that the form on the right-hand side of (3.43) is indeed so, as follows. First, note that it is straightforward to rewrite (3.5) as
$D_{\zeta }$; one can check that the form on the right-hand side of (3.43) is indeed so, as follows. First, note that it is straightforward to rewrite (3.5) as
 \begin{equation} P(\zeta,q)= \kappa(q)\,(\zeta-1)\prod_{n=1}^{\infty}(\zeta^{{-}1}(\zeta-q^{2n})(\zeta-q^{{-}2n})), \end{equation}
\begin{equation} P(\zeta,q)= \kappa(q)\,(\zeta-1)\prod_{n=1}^{\infty}(\zeta^{{-}1}(\zeta-q^{2n})(\zeta-q^{{-}2n})), \end{equation}
where ![]() $\kappa (q)$ is independent of
$\kappa (q)$ is independent of ![]() $\zeta$ (in fact,
$\zeta$ (in fact, ![]() $\kappa (q)=-\prod _{n=1}^{\infty }(-q^{2n})$). Then it is evident that the change in
$\kappa (q)=-\prod _{n=1}^{\infty }(-q^{2n})$). Then it is evident that the change in ![]() $\log P(\zeta,q)$ after
$\log P(\zeta,q)$ after ![]() $\zeta$ completes a circuit around a circle that is centred on the origin and of radius
$\zeta$ completes a circuit around a circle that is centred on the origin and of radius ![]() $\rho$, say, in the anticlockwise direction, is equal to
$\rho$, say, in the anticlockwise direction, is equal to ![]() $0$ if
$0$ if ![]() $q^2<\rho <1$ (since for each
$q^2<\rho <1$ (since for each ![]() $n\geq 1$, the change due to the logarithmic singularity at
$n\geq 1$, the change due to the logarithmic singularity at ![]() $\zeta =q^{2n}$ is cancelled by that due to a logarithmic singularity of opposite strength at the origin), but equal to
$\zeta =q^{2n}$ is cancelled by that due to a logarithmic singularity of opposite strength at the origin), but equal to ![]() $2{\rm \pi} \mathrm {i}$ if
$2{\rm \pi} \mathrm {i}$ if ![]() $1<\rho < q^{-2}$, and so on. For
$1<\rho < q^{-2}$, and so on. For ![]() $\zeta \in D_{\zeta }$, we have
$\zeta \in D_{\zeta }$, we have ![]() $q<|\zeta |<1$, and hence
$q<|\zeta |<1$, and hence ![]() $q^4<|\overline {\zeta _1}\zeta |, |\mathrm {i}\zeta |, |\mathrm {i}q^2\zeta |<1$. It then follows that the terms
$q^4<|\overline {\zeta _1}\zeta |, |\mathrm {i}\zeta |, |\mathrm {i}q^2\zeta |<1$. It then follows that the terms ![]() $\log P(\overline {\zeta _1}\zeta,q^2)$,
$\log P(\overline {\zeta _1}\zeta,q^2)$, ![]() $\log P(\mathrm {i}\zeta,q^2)$ and
$\log P(\mathrm {i}\zeta,q^2)$ and ![]() $\log P(\mathrm {i}q^2\zeta,q^2)$ that appear in (3.43) are all single-valued in
$\log P(\mathrm {i}q^2\zeta,q^2)$ that appear in (3.43) are all single-valued in ![]() $D_{\zeta }$. And
$D_{\zeta }$. And ![]() $K(\mathrm {i}\zeta,q^2)$ and
$K(\mathrm {i}\zeta,q^2)$ and ![]() $K(\mathrm {i}q^2\zeta,q^2)$ are also both single-valued in
$K(\mathrm {i}q^2\zeta,q^2)$ are also both single-valued in ![]() $D_{\zeta }$. However,
$D_{\zeta }$. However, ![]() $\beta _0\log \zeta$ is not single-valued in
$\beta _0\log \zeta$ is not single-valued in ![]() $D_{\zeta }$. Hence
$D_{\zeta }$. Hence
so the integrated form for our map ![]() $z(\zeta )$ is given by (3.43) and is single-valued in
$z(\zeta )$ is given by (3.43) and is single-valued in ![]() $D_{\zeta }$. Condition (3.45) places a constraint on our mapping parameters, as we discuss further in the next subsection.
$D_{\zeta }$. Condition (3.45) places a constraint on our mapping parameters, as we discuss further in the next subsection.
3.5. Specifying parameter values
Our parametrisation depends on the following parameters: ![]() $q$,
$q$, ![]() $\arg \{\zeta _1\}$,
$\arg \{\zeta _1\}$, ![]() $\arg \{\zeta _2\}$,
$\arg \{\zeta _2\}$, ![]() $a$ (which, recall, is real and positive) and
$a$ (which, recall, is real and positive) and ![]() $c$ (which is complex). Trivially, for any values of
$c$ (which is complex). Trivially, for any values of ![]() $q$,
$q$, ![]() $\arg \{\zeta _1\}$ and
$\arg \{\zeta _1\}$ and ![]() $\arg \{\zeta _2\}$, we can fix
$\arg \{\zeta _2\}$, we can fix ![]() $c$ and
$c$ and ![]() $a$ to ensure that
$a$ to ensure that ![]() $z_1=0$ and the length of the hydrofoil is
$z_1=0$ and the length of the hydrofoil is ![]() $1$; more specifically, it follows from (3.43) that we should take
$1$; more specifically, it follows from (3.43) that we should take
 \begin{align}
c&={-}(\beta_1 \log P(q^2,q^2) +\beta_2 \log
P(\mathrm{i}\zeta_1,q^2) +\beta_3 \log
P(\mathrm{i}q^2\zeta_1,q^2)\nonumber\\&\qquad\ +\beta_4\,K(\mathrm{i}\zeta_1,q^2)
+\beta_5\,K(\mathrm{i}q^2\zeta_1,q^2)) \end{align}
\begin{align}
c&={-}(\beta_1 \log P(q^2,q^2) +\beta_2 \log
P(\mathrm{i}\zeta_1,q^2) +\beta_3 \log
P(\mathrm{i}q^2\zeta_1,q^2)\nonumber\\&\qquad\ +\beta_4\,K(\mathrm{i}\zeta_1,q^2)
+\beta_5\,K(\mathrm{i}q^2\zeta_1,q^2)) \end{align}
with
 \begin{align} a=
\Bigl|&\hat{\beta}_1 \log
P(\overline{\zeta_1}\zeta_2,q^2) +\hat{\beta}_2 \log
P(\mathrm{i}\zeta_2,q^2) +\hat{\beta}_3 \log
P(\mathrm{i}q^2\zeta_2,q^2)\nonumber\\ &{}+\hat{\beta}_4\,K(\mathrm{i}\zeta_2,q^2)
+\hat{\beta}_5\,K(\mathrm{i}q^2\zeta_2,q^2) +\hat{c}
\Bigr|^{{-}1}, \end{align}
\begin{align} a=
\Bigl|&\hat{\beta}_1 \log
P(\overline{\zeta_1}\zeta_2,q^2) +\hat{\beta}_2 \log
P(\mathrm{i}\zeta_2,q^2) +\hat{\beta}_3 \log
P(\mathrm{i}q^2\zeta_2,q^2)\nonumber\\ &{}+\hat{\beta}_4\,K(\mathrm{i}\zeta_2,q^2)
+\hat{\beta}_5\,K(\mathrm{i}q^2\zeta_2,q^2) +\hat{c}
\Bigr|^{{-}1}, \end{align}
where here we use ![]() $\hat {\beta }_j$ to denote
$\hat {\beta }_j$ to denote ![]() $\beta _j/a$ for
$\beta _j/a$ for ![]() $j=1,\ldots,5$, and
$j=1,\ldots,5$, and ![]() $\hat {c}$ to denote
$\hat {c}$ to denote ![]() $c/a$. (It is evident that one may factor out
$c/a$. (It is evident that one may factor out ![]() $a$ from our expressions (A11), (A7), (A9), (A1) and (A5) for
$a$ from our expressions (A11), (A7), (A9), (A1) and (A5) for ![]() $\beta _1,\ldots,\beta _5$, and hence also from our expression (3.46) for
$\beta _1,\ldots,\beta _5$, and hence also from our expression (3.46) for ![]() $c$.) Next, in order to fix
$c$.) Next, in order to fix ![]() $\arg \{z_2\}=\alpha$, one could use the condition that one obtains by simply setting
$\arg \{z_2\}=\alpha$, one could use the condition that one obtains by simply setting ![]() $\zeta =\zeta _2$ on the right-hand side of (3.43) and then requiring that the argument of this equals
$\zeta =\zeta _2$ on the right-hand side of (3.43) and then requiring that the argument of this equals ![]() $\alpha$. However, a simpler condition is given by (3.49) below. One may deduce this by noting that it follows from (3.31) and (3.34) (along with both equations in (3.9)) that
$\alpha$. However, a simpler condition is given by (3.49) below. One may deduce this by noting that it follows from (3.31) and (3.34) (along with both equations in (3.9)) that
and hence from (3.38a) (and both equations in (3.9) again) that
Finally, in addition to the above, we must also impose the single-valuedness condition (3.45) with ![]() $\beta _0$ as given by (A12), which one can show is equivalent to
$\beta _0$ as given by (A12), which one can show is equivalent to
Equations (3.49) and (3.50) fix two of the remaining three parameters ![]() $\arg \{\zeta _1\}$,
$\arg \{\zeta _1\}$, ![]() $\arg \{\zeta _2\}$ and
$\arg \{\zeta _2\}$ and ![]() $q$. This leaves one remaining free parameter. As is borne out by the examples presented in § 6, one could interpret this remaining parameter as corresponding in some sense to the depth of the hydrofoil below the free surface. As a measure of this depth, we will adopt the following. Recall that we fix the leading and trailing endpoints of the hydrofoil to be at the origin and
$q$. This leaves one remaining free parameter. As is borne out by the examples presented in § 6, one could interpret this remaining parameter as corresponding in some sense to the depth of the hydrofoil below the free surface. As a measure of this depth, we will adopt the following. Recall that we fix the leading and trailing endpoints of the hydrofoil to be at the origin and ![]() $\mathrm {e}^{\mathrm {i}\alpha }$, respectively. We now seek some convenient reference level for the
$\mathrm {e}^{\mathrm {i}\alpha }$, respectively. We now seek some convenient reference level for the ![]() $y$-coordinate of points on the free surface. As we show next in § 3.6, in general,
$y$-coordinate of points on the free surface. As we show next in § 3.6, in general, ![]() $y$ does not tend to a constant along the free surface as
$y$ does not tend to a constant along the free surface as ![]() $|x|\rightarrow \infty$. However (as is the case for the examples that we present in § 6), it appears that there is a single (finite) point, say
$|x|\rightarrow \infty$. However (as is the case for the examples that we present in § 6), it appears that there is a single (finite) point, say ![]() $z_c$, on the free surface at which
$z_c$, on the free surface at which ![]() $\mathrm {d} y/\mathrm {d} x=0$; there is a peak of the free surface at
$\mathrm {d} y/\mathrm {d} x=0$; there is a peak of the free surface at ![]() $z_c$ when the leading endpoint of the hydrofoil is above its trailing endpoint – i.e. when
$z_c$ when the leading endpoint of the hydrofoil is above its trailing endpoint – i.e. when ![]() $\alpha <0$ – and a trough at
$\alpha <0$ – and a trough at ![]() $z_c$ when
$z_c$ when ![]() $\alpha >0$. Fixing
$\alpha >0$. Fixing ![]() $\mathrm {Im}\{z_c\}=y_c$, say, then essentially fixes the depth of the hydrofoil. This places the following additional condition on our mapping parameters. Of course,
$\mathrm {Im}\{z_c\}=y_c$, say, then essentially fixes the depth of the hydrofoil. This places the following additional condition on our mapping parameters. Of course, ![]() $z_c=z(\zeta _c)$ for some
$z_c=z(\zeta _c)$ for some ![]() $\zeta _c$ on
$\zeta _c$ on ![]() $C_0$ at which
$C_0$ at which ![]() $\mathrm {Im}\{\mathrm {d}z(\zeta )/\mathrm {d}\theta \}=0$, where here we use
$\mathrm {Im}\{\mathrm {d}z(\zeta )/\mathrm {d}\theta \}=0$, where here we use ![]() $\theta$ to denote the angular polar coordinate of
$\theta$ to denote the angular polar coordinate of ![]() $\zeta$. Hence (recalling (3.39)) one may deduce that
$\zeta$. Hence (recalling (3.39)) one may deduce that
and
3.6. Limit as  $|x|\rightarrow \infty$
$|x|\rightarrow \infty$
To conclude this section, we determine the limiting shape of the free surface as ![]() $|x|\rightarrow \infty$. To do so, we consider the limit of
$|x|\rightarrow \infty$. To do so, we consider the limit of ![]() $z(\zeta )$ as given by (3.43) as
$z(\zeta )$ as given by (3.43) as ![]() $\zeta \rightarrow -\mathrm {i}$ along
$\zeta \rightarrow -\mathrm {i}$ along ![]() $C_0$. Equivalently, we may take
$C_0$. Equivalently, we may take ![]() $\zeta =\mathrm {e}^{\mathrm {i}((-{\rm \pi} /2)+\epsilon )}$ and consider the limit of
$\zeta =\mathrm {e}^{\mathrm {i}((-{\rm \pi} /2)+\epsilon )}$ and consider the limit of ![]() $z(\zeta )$ as
$z(\zeta )$ as ![]() $\epsilon \rightarrow 0^{\pm }$. In this limit, the only terms in (3.43) that become singular are
$\epsilon \rightarrow 0^{\pm }$. In this limit, the only terms in (3.43) that become singular are ![]() $\log P(\mathrm {i}\zeta,q^2)$ and
$\log P(\mathrm {i}\zeta,q^2)$ and ![]() $K(\mathrm {i}\zeta,q^2)$; recalling (3.5) and (3.8) (and using series expansions for
$K(\mathrm {i}\zeta,q^2)$; recalling (3.5) and (3.8) (and using series expansions for ![]() $\exp$ and
$\exp$ and ![]() $\log$), one finds that
$\log$), one finds that
Hence, recalling (A1), it follows from (3.43) that in this limit, assuming that ![]() $\beta _2$ and
$\beta _2$ and ![]() $a$ are of the order of
$a$ are of the order of ![]() $1$,
$1$,
But, as shown in Appendix A (see its final paragraph), ![]() $\beta _2$ is purely imaginary. It then follows from (3.54) that as
$\beta _2$ is purely imaginary. It then follows from (3.54) that as ![]() $|x|\rightarrow \infty$, the free surface tends to the curve given by
$|x|\rightarrow \infty$, the free surface tends to the curve given by
Thus the ![]() $y$-coordinate of points on the free surface tends to infinity as
$y$-coordinate of points on the free surface tends to infinity as ![]() $|x|\rightarrow \infty$. SW20 observe the same limiting behaviour for the free surface for flow past a submerged circular cylinder without gravity – see their equation (3.8). The sole exception to this appears to be for
$|x|\rightarrow \infty$. SW20 observe the same limiting behaviour for the free surface for flow past a submerged circular cylinder without gravity – see their equation (3.8). The sole exception to this appears to be for ![]() $\alpha <0$ in the limit when the depth of the hydrofoil below the free surface tends to zero, as in figure 5. Equally, (4.9) and (4.10) show that the lift coefficient
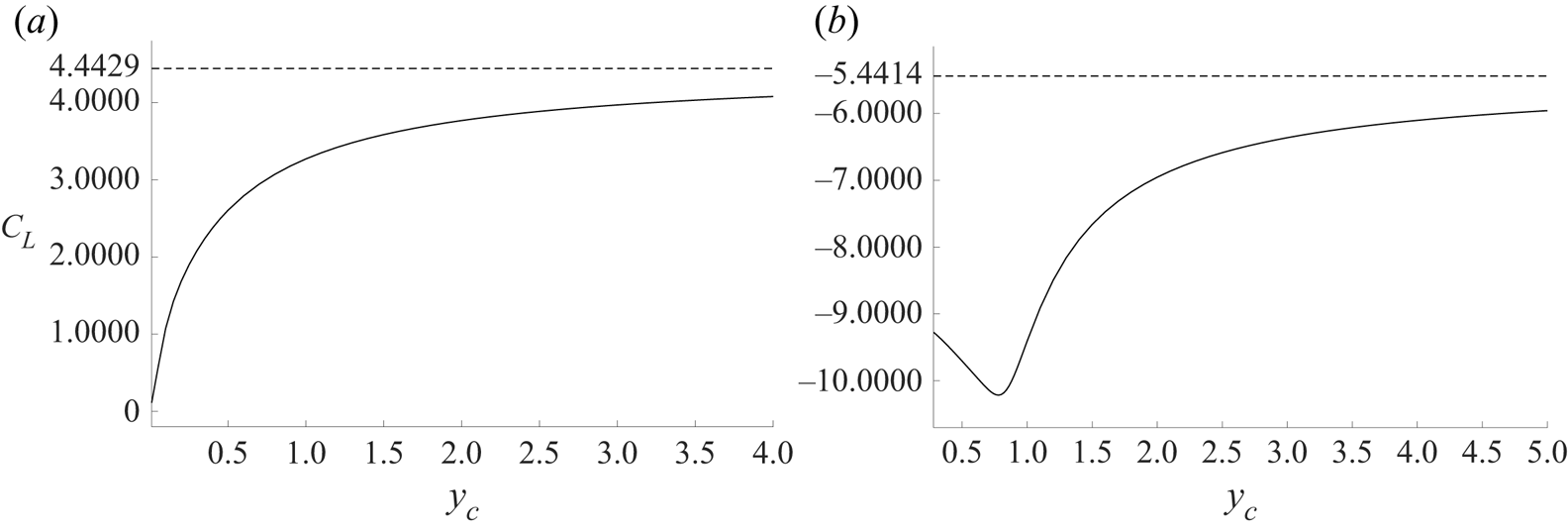
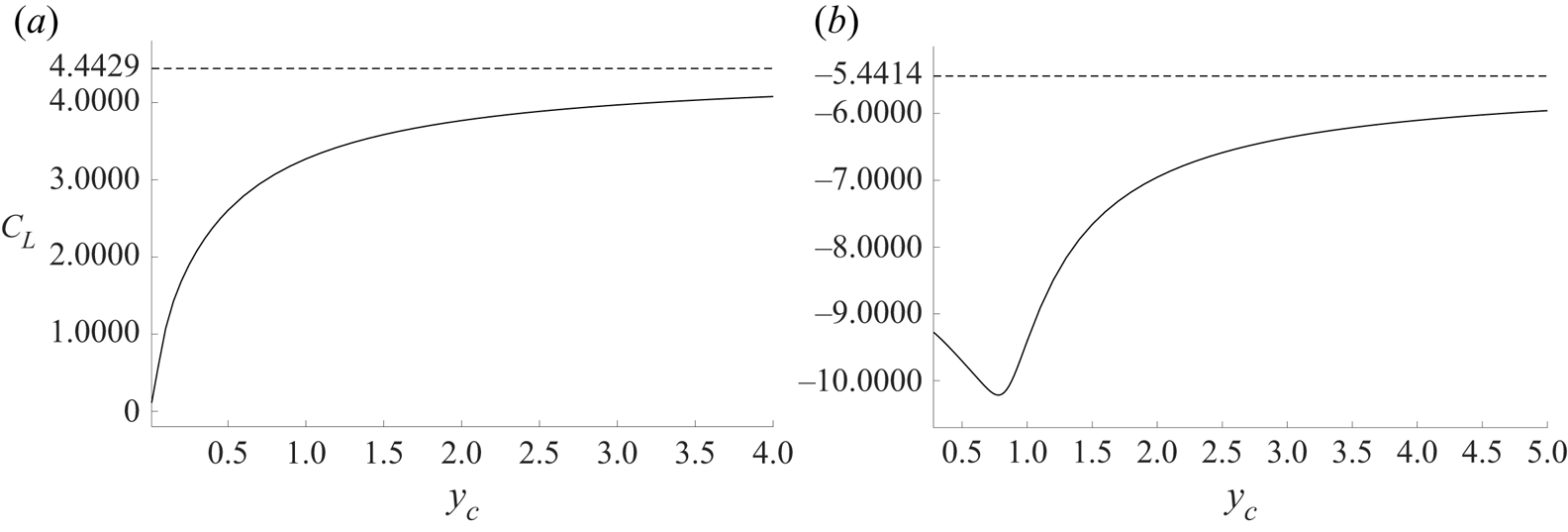
$\alpha <0$ in the limit when the depth of the hydrofoil below the free surface tends to zero, as in figure 5. Equally, (4.9) and (4.10) show that the lift coefficient ![]() $C_L$ is simply a multiple of
$C_L$ is simply a multiple of ![]() $\mathrm {Im}\{\beta _2\}$, and figure 7(a) shows that
$\mathrm {Im}\{\beta _2\}$, and figure 7(a) shows that ![]() $C_L\to 0$ as
$C_L\to 0$ as ![]() $y_c\to 0$ for
$y_c\to 0$ for ![]() $\alpha =-{\rm \pi} /4$.
$\alpha =-{\rm \pi} /4$.

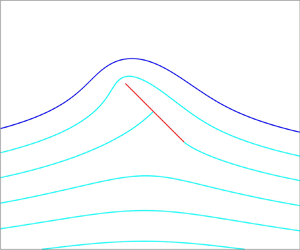
Figure 5. Free surface profiles (blue) for flow past a hydrofoil (red) for various angles of attack ![]() $-\alpha$ and leading-edge submergence
$-\alpha$ and leading-edge submergence ![]() $y_c$: (a)
$y_c$: (a) ![]() $\alpha =-{\rm \pi} /4$,
$\alpha =-{\rm \pi} /4$, ![]() $y_c=0.01, 0.05$ and
$y_c=0.01, 0.05$ and ![]() $0.1, 0.2, 0.3,\dots$; and (b)
$0.1, 0.2, 0.3,\dots$; and (b) ![]() $\alpha ={\rm \pi} /3$,
$\alpha ={\rm \pi} /3$, ![]() $y_c=0.28, 0.8$ and
$y_c=0.28, 0.8$ and ![]() $1.2, 1.4, 1.6, \ldots$. Lengths here and in subsequent figures are normalised on the length of the foil.
$1.2, 1.4, 1.6, \ldots$. Lengths here and in subsequent figures are normalised on the length of the foil.
4. The force on the hydrofoil
We denote the (vector) force that is exerted by the fluid on the hydrofoil by ![]() $\boldsymbol {F}$, and the components of this force in the
$\boldsymbol {F}$, and the components of this force in the ![]() $x$- and
$x$- and ![]() $y$-directions by
$y$-directions by ![]() $F_x$ and
$F_x$ and ![]() $F_y$, respectively. From Blasius's theorem, we have
$F_y$, respectively. From Blasius's theorem, we have
where, as in (2.6), ![]() $\mathcal {C}$ is a simple closed contour that surrounds the hydrofoil, and we integrate around
$\mathcal {C}$ is a simple closed contour that surrounds the hydrofoil, and we integrate around ![]() $\mathcal {C}$ in the anticlockwise direction, and
$\mathcal {C}$ in the anticlockwise direction, and ![]() $\rho$ is the density of the fluid. Using (3.3), we can write the integral in (4.1) in terms of
$\rho$ is the density of the fluid. Using (3.3), we can write the integral in (4.1) in terms of ![]() $\zeta$ as
$\zeta$ as
where we can take ![]() $\hat {\mathcal {C}}$ to be as in (3.18), and we integrate around it in the anticlockwise direction. We can in fact compute the integral in (4.2) analytically, as follows.
$\hat {\mathcal {C}}$ to be as in (3.18), and we integrate around it in the anticlockwise direction. We can in fact compute the integral in (4.2) analytically, as follows.
First, let us introduce the function
One may determine ![]() $\eta (\zeta )$ by following an approach similar to that which we used to determine the function
$\eta (\zeta )$ by following an approach similar to that which we used to determine the function ![]() $H(\zeta )$ in § 3.4 (and
$H(\zeta )$ in § 3.4 (and ![]() $\varOmega (\zeta )$ previously). First, it follows from (3.25) and (3.33) that
$\varOmega (\zeta )$ previously). First, it follows from (3.25) and (3.33) that
so ![]() $\eta (\zeta )$ is automorphic with respect to
$\eta (\zeta )$ is automorphic with respect to ![]() $\hat {\varTheta }$. Next, one can check from the properties of
$\hat {\varTheta }$. Next, one can check from the properties of ![]() $W'(\zeta )$ and
$W'(\zeta )$ and ![]() $\varOmega (\zeta )$ that
$\varOmega (\zeta )$ that ![]() $\eta (\zeta )$ is analytic everywhere in
$\eta (\zeta )$ is analytic everywhere in ![]() $\hat {F}$ except for a simple pole at
$\hat {F}$ except for a simple pole at ![]() $\zeta =\zeta _1$, and double poles at
$\zeta =\zeta _1$, and double poles at ![]() $\zeta =-\mathrm {i}$ and
$\zeta =-\mathrm {i}$ and ![]() $-\mathrm {i}q^2$. It then follows that we can write
$-\mathrm {i}q^2$. It then follows that we can write
for some unique constants ![]() $\gamma _0,\ldots,\gamma _5$. Before attempting to determine these, note that, evidently, we can write (4.2) as
$\gamma _0,\ldots,\gamma _5$. Before attempting to determine these, note that, evidently, we can write (4.2) as
But then, by arguments similar to those that we used when integrating ![]() $H(\zeta )/\zeta$ (with
$H(\zeta )/\zeta$ (with ![]() $H(\zeta )$ given by (3.42)) in § 3.4 (in particular, see text between (3.43) and (3.45)), one can compute the integral of
$H(\zeta )$ given by (3.42)) in § 3.4 (in particular, see text between (3.43) and (3.45)), one can compute the integral of ![]() $\eta (\zeta )/\zeta$ that appears in (4.6) (with
$\eta (\zeta )/\zeta$ that appears in (4.6) (with ![]() $\eta (\zeta )$ given by (4.5)) analytically; one finds simply that
$\eta (\zeta )$ given by (4.5)) analytically; one finds simply that
Thus, in order to determine ![]() $\boldsymbol {F}$, it remains only to determine the sum
$\boldsymbol {F}$, it remains only to determine the sum ![]() $\gamma _0+\gamma _1$. We do so in Appendix B – see in particular (B3) – showing that it is simply a multiple of
$\gamma _0+\gamma _1$. We do so in Appendix B – see in particular (B3) – showing that it is simply a multiple of ![]() $\beta _2$. It then follows from (4.6), (4.7) and (B3) that
$\beta _2$. It then follows from (4.6), (4.7) and (B3) that
Appendix A shows ![]() $\beta _2$ to be purely imaginary. It then follows from (4.8) that
$\beta _2$ to be purely imaginary. It then follows from (4.8) that ![]() $\boldsymbol {F}$ has only a vertical component (i.e.
$\boldsymbol {F}$ has only a vertical component (i.e. ![]() $F_x=0$), given by
$F_x=0$), given by
The lift coefficient ![]() $C_L$ for a two-dimensional lifting surface is defined as the force (per unit width in the spanwise direction) in the direction perpendicular to the oncoming flow at infinity, scaled on
$C_L$ for a two-dimensional lifting surface is defined as the force (per unit width in the spanwise direction) in the direction perpendicular to the oncoming flow at infinity, scaled on ![]() $\tfrac {1}{2} \rho U^2 \ell$, where
$\tfrac {1}{2} \rho U^2 \ell$, where ![]() $\ell$ is the length of the chord of the lifting surface. Here, the normalisation gives
$\ell$ is the length of the chord of the lifting surface. Here, the normalisation gives ![]() $\ell =1$, so
$\ell =1$, so
with ![]() $F_y$ given by (4.9) (and
$F_y$ given by (4.9) (and ![]() $\beta _2$ by (A7)). Section 6 discusses the behaviour of
$\beta _2$ by (A7)). Section 6 discusses the behaviour of ![]() $C_L$ as a function of
$C_L$ as a function of ![]() $\alpha$ and
$\alpha$ and ![]() $y_c$.
$y_c$.
5. Limiting cases
5.1. A horizontal hydrofoil
In deriving our parametrisation, we have assumed that ![]() $\zeta _1\neq -\overline {\zeta _2}$ (see just after (3.36)), i.e. that
$\zeta _1\neq -\overline {\zeta _2}$ (see just after (3.36)), i.e. that ![]() $\zeta _1$ and
$\zeta _1$ and ![]() $\zeta _2$ are not reflections of one another in the imaginary
$\zeta _2$ are not reflections of one another in the imaginary ![]() $\zeta$-axis. However, let us now consider the limit of our results as
$\zeta$-axis. However, let us now consider the limit of our results as ![]() $-\zeta _1/\overline {\zeta _2}\rightarrow 1$. First, in this limit, it is evident from (3.38a,b) and (3.37) that (since
$-\zeta _1/\overline {\zeta _2}\rightarrow 1$. First, in this limit, it is evident from (3.38a,b) and (3.37) that (since ![]() $K(-\zeta _1/\overline {\zeta _2},q^2)$ becomes unbounded)
$K(-\zeta _1/\overline {\zeta _2},q^2)$ becomes unbounded) ![]() $\alpha _1=\alpha _2=0$ and
$\alpha _1=\alpha _2=0$ and ![]() $\alpha _0=U$, and hence, as follows from (3.34),
$\alpha _0=U$, and hence, as follows from (3.34), ![]() $\varOmega (\zeta )=U$ for all
$\varOmega (\zeta )=U$ for all ![]() $\zeta$. Thus
$\zeta$. Thus ![]() $w'(z)=U$ for all
$w'(z)=U$ for all ![]() $z$. It follows that in this case the hydrofoil must be horizontal. Indeed, it follows that in this case our expressions for the constants
$z$. It follows that in this case the hydrofoil must be horizontal. Indeed, it follows that in this case our expressions for the constants ![]() $\beta _1,\ldots,\beta _5$ – see Appendix A – reduce to
$\beta _1,\ldots,\beta _5$ – see Appendix A – reduce to
and hence our expression (3.43) for ![]() $z(\zeta )$ reduces to
$z(\zeta )$ reduces to
where we have made use of (3.15a). And one can check by using the properties of ![]() $K(\zeta,q)$ that
$K(\zeta,q)$ that ![]() $z(\zeta )$ as given by (5.2) maps
$z(\zeta )$ as given by (5.2) maps ![]() $C_1$ onto a horizontal line segment of finite length. Furthermore, one can also check that it maps
$C_1$ onto a horizontal line segment of finite length. Furthermore, one can also check that it maps ![]() $C_0$ onto a horizontal line that extends to infinity in both directions – this is the free surface in this case. We also mention that in this case, it follows from (5.1a,b) (and (3.15b)) that
$C_0$ onto a horizontal line that extends to infinity in both directions – this is the free surface in this case. We also mention that in this case, it follows from (5.1a,b) (and (3.15b)) that ![]() $\beta _0$ – as given by (A12) – reduces to
$\beta _0$ – as given by (A12) – reduces to
And since ![]() $z'(\zeta _1)=0$, it follows from (5.2) (and (3.10)) that
$z'(\zeta _1)=0$, it follows from (5.2) (and (3.10)) that ![]() $L(\mathrm {i}\zeta _1,q)=0$, and hence from (5.3) that
$L(\mathrm {i}\zeta _1,q)=0$, and hence from (5.3) that ![]() $\beta _0=0$. Thus in this case, the single-valuedness condition (3.45) is satisfied automatically. For a similar reason, it follows from (3.23) that the circulation
$\beta _0=0$. Thus in this case, the single-valuedness condition (3.45) is satisfied automatically. For a similar reason, it follows from (3.23) that the circulation ![]() $\varGamma$ around the hydrofoil in this case is also
$\varGamma$ around the hydrofoil in this case is also ![]() $0$. Furthermore, it follows from (4.9) (and the fact that now
$0$. Furthermore, it follows from (4.9) (and the fact that now ![]() $\beta _2=0$) that in this case, the fluid exerts no force on the hydrofoil.
$\beta _2=0$) that in this case, the fluid exerts no force on the hydrofoil.
5.2. Near-vertical hydrofoils
We have also thus far assumed that ![]() $-\overline {\zeta _2}\neq \zeta _2$, or equivalently, that
$-\overline {\zeta _2}\neq \zeta _2$, or equivalently, that ![]() $\zeta _2\neq \pm \mathrm {i}q$ (see just after (3.24)). Let us now consider the limits of our results as
$\zeta _2\neq \pm \mathrm {i}q$ (see just after (3.24)). Let us now consider the limits of our results as ![]() $\zeta _2\rightarrow \pm \mathrm {i}q$ whilst
$\zeta _2\rightarrow \pm \mathrm {i}q$ whilst ![]() $\zeta _1\rightarrow \mp \mathrm {i}q$, respectively. First, in both of these limits, it is evident from (3.38a) that
$\zeta _1\rightarrow \mp \mathrm {i}q$, respectively. First, in both of these limits, it is evident from (3.38a) that ![]() $\alpha _1$ must be real, and hence, as follows from (3.48), that
$\alpha _1$ must be real, and hence, as follows from (3.48), that ![]() $\alpha$ must tend to either of
$\alpha$ must tend to either of ![]() $\pm {\rm \pi}/2$. On geometrical grounds, one may deduce that
$\pm {\rm \pi}/2$. On geometrical grounds, one may deduce that ![]() $\alpha \rightarrow \pm {\rm \pi}/2$ as
$\alpha \rightarrow \pm {\rm \pi}/2$ as ![]() $\zeta _2\rightarrow \pm \mathrm {i}q$, respectively. Indeed, it then follows from (A1), (A5), (A9), (A11), and the fact (already stated) that
$\zeta _2\rightarrow \pm \mathrm {i}q$, respectively. Indeed, it then follows from (A1), (A5), (A9), (A11), and the fact (already stated) that ![]() $\beta _2$ is purely imaginary, that in both of these limits,
$\beta _2$ is purely imaginary, that in both of these limits, ![]() $\beta _1$,
$\beta _1$, ![]() $\beta _3$,
$\beta _3$, ![]() $\beta _4$ and
$\beta _4$ and ![]() $\beta _5$ are also all purely imaginary, and
$\beta _5$ are also all purely imaginary, and
One can then check by using the properties of ![]() $P(\zeta,q)$ and
$P(\zeta,q)$ and ![]() $K(\zeta,q)$ that
$K(\zeta,q)$ that ![]() $z(\zeta )$ as given by (3.43) maps
$z(\zeta )$ as given by (3.43) maps ![]() $C_1$ onto a vertical line segment of finite length. We also mention that in this case, it follows (using the facts that
$C_1$ onto a vertical line segment of finite length. We also mention that in this case, it follows (using the facts that ![]() $K(\pm q,q^2)=-K(\pm q^3,q^2)$ and
$K(\pm q,q^2)=-K(\pm q^3,q^2)$ and ![]() $L(\pm q,q^2)=L(\pm q^3,q^2)$, which follow from (3.9) and (3.12), respectively) that
$L(\pm q,q^2)=L(\pm q^3,q^2)$, which follow from (3.9) and (3.12), respectively) that ![]() $\beta _0$ (as given by (A12)) is automatically equal to
$\beta _0$ (as given by (A12)) is automatically equal to ![]() $0$, so the single-valuedness condition (3.45) is satisfied automatically.
$0$, so the single-valuedness condition (3.45) is satisfied automatically.
6. Flow properties
We have evaluated the solution obtained above using our parametrisation, for a hydrofoil of unit length with leading edge ![]() $z_1$ at the origin and trailing edge
$z_1$ at the origin and trailing edge ![]() $z_2$ at
$z_2$ at ![]() $\mathrm {e}^{\mathrm {i}\alpha }$ for some
$\mathrm {e}^{\mathrm {i}\alpha }$ for some ![]() $\alpha$, giving an angle of attack
$\alpha$, giving an angle of attack ![]() $-\alpha$. It is sufficient for a valid solution to fix two of
$-\alpha$. It is sufficient for a valid solution to fix two of ![]() $\arg \{\zeta _1\}$,
$\arg \{\zeta _1\}$, ![]() $\arg \{\zeta _2\}$ and
$\arg \{\zeta _2\}$ and ![]() $q$, and then solve the single equation (3.50), with
$q$, and then solve the single equation (3.50), with ![]() $\alpha$ defined by (3.49), for the third. To obtain a normalised solution, however, we fixed
$\alpha$ defined by (3.49), for the third. To obtain a normalised solution, however, we fixed ![]() $\alpha$ and
$\alpha$ and ![]() $y_c$ (the depth of submergence of the leading edge), set
$y_c$ (the depth of submergence of the leading edge), set ![]() $U$ and
$U$ and ![]() $\rho$ to unity, and solved (3.49)–(3.52) simultaneously for the four real numbers
$\rho$ to unity, and solved (3.49)–(3.52) simultaneously for the four real numbers ![]() $\arg \{\zeta _1\}$,
$\arg \{\zeta _1\}$, ![]() $\arg \{\zeta _2\}$,
$\arg \{\zeta _2\}$, ![]() $q$ and
$q$ and ![]() $\arg \{\zeta _c\}$ using a multi-dimensional Newton-type iterative method. All computations were carried out in MATLAB. The functions
$\arg \{\zeta _c\}$ using a multi-dimensional Newton-type iterative method. All computations were carried out in MATLAB. The functions ![]() $P(\zeta,q)$,
$P(\zeta,q)$, ![]() $K(\zeta,q)$ and
$K(\zeta,q)$ and ![]() $L(\zeta,q)$ were evaluated from finite truncations of the infinite product in (3.5) and the infinite series in (3.8) and (3.11), respectively. For the largest values of
$L(\zeta,q)$ were evaluated from finite truncations of the infinite product in (3.5) and the infinite series in (3.8) and (3.11), respectively. For the largest values of ![]() $q$ used (of the order of 0.95), 150 terms gave 16-decimal-place accuracy, while for the smallest values of
$q$ used (of the order of 0.95), 150 terms gave 16-decimal-place accuracy, while for the smallest values of ![]() $q$, three terms were sufficient. The computations were so rapid that no optimisation was necessary and all computations were performed with 200 terms. The routine fsolve was used for the Newton-type root finding. Once the parameters for a given plate orientation are determined, the value of any quantity follows simply by evaluating an explicit formula. Results can thus be obtained and plotted at machine precision as, for example, in figure 6(e).
$q$, three terms were sufficient. The computations were so rapid that no optimisation was necessary and all computations were performed with 200 terms. The routine fsolve was used for the Newton-type root finding. Once the parameters for a given plate orientation are determined, the value of any quantity follows simply by evaluating an explicit formula. Results can thus be obtained and plotted at machine precision as, for example, in figure 6(e).

Figure 6. Streamlines (turquoise) for free-surface flow past a hydrofoil for various angles of attack ![]() $-\alpha$ and leading-edge submergence
$-\alpha$ and leading-edge submergence ![]() $y_c$: (a)
$y_c$: (a) ![]() $\alpha =-{\rm \pi} /4$,
$\alpha =-{\rm \pi} /4$, ![]() $y_c=1.5$; (b)
$y_c=1.5$; (b) ![]() $\alpha =-{\rm \pi} /4$,
$\alpha =-{\rm \pi} /4$, ![]() $y_c=0.3$; (c)
$y_c=0.3$; (c) ![]() $\alpha ={\rm \pi} /3$,
$\alpha ={\rm \pi} /3$, ![]() $y_c=1.4$; and (d)
$y_c=1.4$; and (d) ![]() $\alpha ={\rm \pi} /3$,
$\alpha ={\rm \pi} /3$, ![]() $y_c=0.28$. (e) A detail of part (d) near the stagnation point.
$y_c=0.28$. (e) A detail of part (d) near the stagnation point.
Figure 5 shows free surface profiles for flow past a hydrofoil at angles ![]() $\alpha =-{\rm \pi} /4$ and
$\alpha =-{\rm \pi} /4$ and ![]() ${\rm \pi} /3$, for different values of leading-edge submergence
${\rm \pi} /3$, for different values of leading-edge submergence ![]() $y_c$. Figure 6 gives further examples, including sub-surface streamlines (turquoise). For positive angles of attack (
$y_c$. Figure 6 gives further examples, including sub-surface streamlines (turquoise). For positive angles of attack (![]() $\alpha <0$), the free surface has a crest (at
$\alpha <0$), the free surface has a crest (at ![]() $z_c$), while for negative angles of attack (
$z_c$), while for negative angles of attack (![]() $\alpha >0$), the surface has a trough. These results are consistent with those for a submerged cylinder in zero gravity in SW20. In terms of the mapping parameters, it appears that for all
$\alpha >0$), the surface has a trough. These results are consistent with those for a submerged cylinder in zero gravity in SW20. In terms of the mapping parameters, it appears that for all ![]() $\alpha$,
$\alpha$, ![]() $y_c\rightarrow \infty$ corresponds to
$y_c\rightarrow \infty$ corresponds to ![]() $q\rightarrow 0$, while
$q\rightarrow 0$, while ![]() $y_c$ decreases as
$y_c$ decreases as ![]() $q\rightarrow 1$. In particular, for
$q\rightarrow 1$. In particular, for ![]() $\alpha =-{\rm \pi} /4$, for
$\alpha =-{\rm \pi} /4$, for ![]() $y_c=0.01$, we have
$y_c=0.01$, we have ![]() $q=0.9399$ (to four decimal places – we report other values to the same accuracy),
$q=0.9399$ (to four decimal places – we report other values to the same accuracy), ![]() $\arg \{\zeta _1\}=1.6885$,
$\arg \{\zeta _1\}=1.6885$, ![]() $\arg \{\zeta _2\}=4.7471$ and
$\arg \{\zeta _2\}=4.7471$ and ![]() $\arg \{\zeta _c\}=1.6537$, while for
$\arg \{\zeta _c\}=1.6537$, while for ![]() $y_c=1.5$, we have
$y_c=1.5$, we have ![]() $q=0.0735$,
$q=0.0735$, ![]() $\arg \{\zeta _1\}=2.4593$,
$\arg \{\zeta _1\}=2.4593$, ![]() $\arg \{\zeta _2\}=5.4119$ and
$\arg \{\zeta _2\}=5.4119$ and ![]() $\arg \{\zeta _c\}=1.7598$.
$\arg \{\zeta _c\}=1.7598$.
For ![]() $\alpha =-{\rm \pi} /4$ in figure 5(a), it appears that solutions exist for all
$\alpha =-{\rm \pi} /4$ in figure 5(a), it appears that solutions exist for all ![]() $y_c>0$. In the limit as
$y_c>0$. In the limit as ![]() $y_c\rightarrow 0$, the free surface ‘shrinks’ onto the hydrofoil, extending horizontally from the trailing edge to infinity in both directions. Figure 7(a) shows that
$y_c\rightarrow 0$, the free surface ‘shrinks’ onto the hydrofoil, extending horizontally from the trailing edge to infinity in both directions. Figure 7(a) shows that ![]() $C_L$ is a positive, monotonic increasing function of
$C_L$ is a positive, monotonic increasing function of ![]() $y_c$, thus from (4.9) and (4.10), so too is
$y_c$, thus from (4.9) and (4.10), so too is ![]() $\mathrm {Im}\{\beta _2\}$. The asymptotic form (3.55) then implies that any solution for the free surface for a given
$\mathrm {Im}\{\beta _2\}$. The asymptotic form (3.55) then implies that any solution for the free surface for a given ![]() $y_c$ will eventually, at sufficiently large
$y_c$ will eventually, at sufficiently large ![]() $|x|$, cut the free surface of all solutions for larger values of
$|x|$, cut the free surface of all solutions for larger values of ![]() $y_c$. This is particularly evident when
$y_c$. This is particularly evident when ![]() $y_c=0.01$ and the free surface is close to horizontal in the range shown.
$y_c=0.01$ and the free surface is close to horizontal in the range shown.
For ![]() $\alpha ={\rm \pi} /3$ in figure 5(b), it appears that there exist solutions for all
$\alpha ={\rm \pi} /3$ in figure 5(b), it appears that there exist solutions for all ![]() $y_c$ greater than some lower bound slightly less than
$y_c$ greater than some lower bound slightly less than ![]() $0.28$, at which the free surface develops a cusp (at
$0.28$, at which the free surface develops a cusp (at ![]() $z_c$) with
$z_c$) with ![]() $q=0.9565$,
$q=0.9565$, ![]() $\arg \{\zeta _1\}=4.6982$,
$\arg \{\zeta _1\}=4.6982$, ![]() $\arg \{\zeta _2\}=4.8212$ and
$\arg \{\zeta _2\}=4.8212$ and ![]() $\arg \{\zeta _c\}=4.5894$. As in figure 5(a), the free surfaces of solutions for different values of
$\arg \{\zeta _c\}=4.5894$. As in figure 5(a), the free surfaces of solutions for different values of ![]() $y_c$ intersect if the corresponding values of
$y_c$ intersect if the corresponding values of ![]() $C_L$ differ, as they do in general. Figure 7(b) shows that
$C_L$ differ, as they do in general. Figure 7(b) shows that ![]() $C_L$ is no longer a monotonic function of
$C_L$ is no longer a monotonic function of ![]() $y_c$, so there exist pairs of values of
$y_c$, so there exist pairs of values of ![]() $y_c$ for which the free surfaces of the corresponding solutions become parallel at sufficiently large
$y_c$ for which the free surfaces of the corresponding solutions become parallel at sufficiently large ![]() $|x|$, although they may intersect at finite
$|x|$, although they may intersect at finite ![]() $x$.
$x$.
The free surface for ![]() $\alpha =-{\rm \pi} /4$ with
$\alpha =-{\rm \pi} /4$ with ![]() $y_c=0.01$, and that for
$y_c=0.01$, and that for ![]() $\alpha ={\rm \pi} /3$ with
$\alpha ={\rm \pi} /3$ with ![]() $y_c=0.28$, do not make contact with the hydrofoil. This is clearer in figure 6(e), which shows a detail of figure 6(d) in the neighbourhood of the stagnation point. The free surface almost coincides with the stagnation point streamline and then passes closely along the rear of the upper surface of the foil.
$y_c=0.28$, do not make contact with the hydrofoil. This is clearer in figure 6(e), which shows a detail of figure 6(d) in the neighbourhood of the stagnation point. The free surface almost coincides with the stagnation point streamline and then passes closely along the rear of the upper surface of the foil.
Figure 7 quantifies the reduction in the lift coefficient with decreasing leading-edge submergence ![]() $y_c$ at the fixed angles of attack
$y_c$ at the fixed angles of attack ![]() ${\rm \pi} /4$ (
${\rm \pi} /4$ (![]() $\alpha =-{\rm \pi} /4$) and
$\alpha =-{\rm \pi} /4$) and ![]() $-{\rm \pi} /3$ (
$-{\rm \pi} /3$ (![]() $\alpha ={\rm \pi} /3$). The dashed lines give the values for a foil in unbounded flow,
$\alpha ={\rm \pi} /3$). The dashed lines give the values for a foil in unbounded flow,
to which the graphs asymptote as ![]() $y_c\to \infty$. For
$y_c\to \infty$. For ![]() $\alpha =-{\rm \pi} /4$, it appears that
$\alpha =-{\rm \pi} /4$, it appears that ![]() $C_L\rightarrow 0$ as
$C_L\rightarrow 0$ as ![]() $y_c\rightarrow 0$ (the smallest value of
$y_c\rightarrow 0$ (the smallest value of ![]() $C_L$ plotted here is for
$C_L$ plotted here is for ![]() $y_c=0.01$).
$y_c=0.01$).
Figure 8(a) shows the lift coefficient ![]() $C_L$ as a function of the angle of attack
$C_L$ as a function of the angle of attack ![]() $-\alpha$ for three values of the parameter
$-\alpha$ for three values of the parameter ![]() $h$, defined as the depth of the midpoint of the foil below the central extremum of the free surface, to coincide with the parameter
$h$, defined as the depth of the midpoint of the foil below the central extremum of the free surface, to coincide with the parameter ![]() $h$ in SW20, and related to the leading-edge submergence
$h$ in SW20, and related to the leading-edge submergence ![]() $y_c$ here through
$y_c$ here through
For positive angles of attack, the lift decreases monotonically with ![]() $h$ as expected. Perhaps less expected, once the foil is closer to the surface than a distance of order the chord length of the hydrofoil, the lift no longer increases monotonically with angle of attack: for
$h$ as expected. Perhaps less expected, once the foil is closer to the surface than a distance of order the chord length of the hydrofoil, the lift no longer increases monotonically with angle of attack: for ![]() $h=0.6$ and
$h=0.6$ and ![]() $-\alpha >0.6$, the lift decreases with increasing
$-\alpha >0.6$, the lift decreases with increasing ![]() $-\alpha$. As noted briefly in § 7, the small
$-\alpha$. As noted briefly in § 7, the small ![]() $|\alpha |$ regime is the most likely to be observed in practice, and here figure 8(a) shows that for both positive and negative angles of attack, reducing submergence reduces the magnitude of
$|\alpha |$ regime is the most likely to be observed in practice, and here figure 8(a) shows that for both positive and negative angles of attack, reducing submergence reduces the magnitude of ![]() $C_L$. This reduction is quantified in figure 8(b) which shows, as a function of the depth
$C_L$. This reduction is quantified in figure 8(b) which shows, as a function of the depth ![]() $h$,
$h$,
the slope at the origin of the graphs in figure 8(a), giving the rate of change of ![]() $C_L$ with angle of attack for zero angle of attack, and showing this to decrease rapidly with decreasing submergence at depths comparable to or smaller than the foil chord length.
$C_L$ with angle of attack for zero angle of attack, and showing this to decrease rapidly with decreasing submergence at depths comparable to or smaller than the foil chord length.

Figure 8. (a) The lift coefficient ![]() $C_L$ as a function of the angle of attack
$C_L$ as a function of the angle of attack ![]() $-\alpha$ for three depths
$-\alpha$ for three depths ![]() $h$ of the midpoint of the hydrofoil. (b) The rate of change of
$h$ of the midpoint of the hydrofoil. (b) The rate of change of ![]() $C_L$ with respect to angle of attack
$C_L$ with respect to angle of attack ![]() $-\alpha$ at
$-\alpha$ at ![]() $\alpha =0$, as a function of
$\alpha =0$, as a function of ![]() $h$. The dashed line gives the infinite depth asymptote
$h$. The dashed line gives the infinite depth asymptote ![]() $(\mathrm{d}C_L/\mathrm{d}(-\alpha))|_{\alpha=0}=2{\rm \pi}$ from (6.1).
$(\mathrm{d}C_L/\mathrm{d}(-\alpha))|_{\alpha=0}=2{\rm \pi}$ from (6.1).
The pressure coefficient at each point along the foil is defined as
evaluated on the foil, where ![]() $p$ is the local pressure,
$p$ is the local pressure, ![]() $p_\infty$ is the constant pressure at large distances, and the expression in terms of velocity follows from Bernoulli's equation. Figure 9(a) shows
$p_\infty$ is the constant pressure at large distances, and the expression in terms of velocity follows from Bernoulli's equation. Figure 9(a) shows ![]() $C_p$ for a foil at angle of attack
$C_p$ for a foil at angle of attack ![]() $5^{\circ }$ and various depths of midpoint submergence
$5^{\circ }$ and various depths of midpoint submergence ![]() $h$. At the stagnation point near the leading edge on the lower side of the foil,
$h$. At the stagnation point near the leading edge on the lower side of the foil, ![]() $C_p=1$ as expected, and at the velocity singularity at the leading edge, the pressure diverges to negative infinity. As in the results for the NACA0012 hydrofoil at Froude number
$C_p=1$ as expected, and at the velocity singularity at the leading edge, the pressure diverges to negative infinity. As in the results for the NACA0012 hydrofoil at Froude number ![]() $ {\textit {Fr}}=2$ (with
$ {\textit {Fr}}=2$ (with ![]() $ {\textit {Fr}}=U/\sqrt {g\ell }$, for gravitational acceleration
$ {\textit {Fr}}=U/\sqrt {g\ell }$, for gravitational acceleration ![]() $g$) in figure 11 of SW20, the pressure distribution on the lower side is practically invariant under changes in submergence. The pressure along the upper side decreases rapidly to the far-field value
$g$) in figure 11 of SW20, the pressure distribution on the lower side is practically invariant under changes in submergence. The pressure along the upper side decreases rapidly to the far-field value ![]() $p_\infty$ as the foil nears the surface, leading to a rapid decrease in lift as in figure 7(a). The rounded leading edge of the NACA0012 hydrofoil means that the pressure remains finite there.
$p_\infty$ as the foil nears the surface, leading to a rapid decrease in lift as in figure 7(a). The rounded leading edge of the NACA0012 hydrofoil means that the pressure remains finite there.

Figure 9. (a) The pressure coefficient ![]() $C_p$ for a foil at angle of attack
$C_p$ for a foil at angle of attack ![]() $5^{\circ }$ at selected depths
$5^{\circ }$ at selected depths ![]() $h$ of midpoint submergence as a function of distance
$h$ of midpoint submergence as a function of distance ![]() $\hat {x}$ along the foil from the midpoint. The upper curves correspond to the lower side of the foil, and the lower curves correspond to the upper side. (b) The lift coefficient
$\hat {x}$ along the foil from the midpoint. The upper curves correspond to the lower side of the foil, and the lower curves correspond to the upper side. (b) The lift coefficient ![]() $C_L$ (yellow) as a function of the midpoint submergence
$C_L$ (yellow) as a function of the midpoint submergence ![]() $h$ compared with the values of
$h$ compared with the values of ![]() $C_L$ in SW20 for flow past the NACA0012 hydrofoil at Froude numbers
$C_L$ in SW20 for flow past the NACA0012 hydrofoil at Froude numbers ![]() $ {\textit {Fr}}=5$ (blue) and
$ {\textit {Fr}}=5$ (blue) and ![]() $ {\textit {Fr}}=10$ (red). The dashed line gives the infinite depth asymptote from (6.1).
$ {\textit {Fr}}=10$ (red). The dashed line gives the infinite depth asymptote from (6.1).
Figure 9(b) shows the lift coefficient ![]() $C_L$ as a function of the submergence, comparing the result here with those for the NACA0012 hydrofoil at Froude numbers
$C_L$ as a function of the submergence, comparing the result here with those for the NACA0012 hydrofoil at Froude numbers ![]() $ {\textit {Fr}}=5,10$ in figure 12 of SW20 (which shows, in fact,
$ {\textit {Fr}}=5,10$ in figure 12 of SW20 (which shows, in fact, ![]() $C_L/2$ as in figure 4 of SW20; Dr Y.A. Semenov, private communication) obtained by integrating numerically the Blasius formula (4.1). The analytical solution coincides remarkably with the values for
$C_L/2$ as in figure 4 of SW20; Dr Y.A. Semenov, private communication) obtained by integrating numerically the Blasius formula (4.1). The analytical solution coincides remarkably with the values for ![]() $ {\textit {Fr}}=5$, particularly for submergences
$ {\textit {Fr}}=5$, particularly for submergences ![]() $h<0.6$ and
$h<0.6$ and ![]() $h>3$, but deviating by less than 3.5 % for
$h>3$, but deviating by less than 3.5 % for ![]() $0.6< h<3$. This accords with the results in SW20 figure 6(a) for flow past a cylinder at
$0.6< h<3$. This accords with the results in SW20 figure 6(a) for flow past a cylinder at ![]() $Fr=5$ that show that surface waves are absent at sufficiently large submergence (as they are for all Froude numbers, with the flow approaching flow in an unbounded domain) but also that surface waves disappear for sufficiently small submergence, being negligible at
$Fr=5$ that show that surface waves are absent at sufficiently large submergence (as they are for all Froude numbers, with the flow approaching flow in an unbounded domain) but also that surface waves disappear for sufficiently small submergence, being negligible at ![]() $Fr=5$ for submergence
$Fr=5$ for submergence ![]() $0.43 \ell$ (for cylinder radius
$0.43 \ell$ (for cylinder radius ![]() $\ell$). The difference of the analytical results for
$\ell$). The difference of the analytical results for ![]() $ {\textit {Fr}}\gg 1$ from the results for
$ {\textit {Fr}}\gg 1$ from the results for ![]() $Fr=10$ in SW20 could be expected to be smaller than the difference from the results for
$Fr=10$ in SW20 could be expected to be smaller than the difference from the results for ![]() $Fr=5$, but figure 9(b) shows this not to be so. The reason is unclear but is likely to be due to the geometric differences between the flat plate and the NACA0012 foil. The analytical formula seems nevertheless to capture the general behaviour of the SW20 solutions.
$Fr=5$, but figure 9(b) shows this not to be so. The reason is unclear but is likely to be due to the geometric differences between the flat plate and the NACA0012 foil. The analytical formula seems nevertheless to capture the general behaviour of the SW20 solutions.
7. Discussion
We have presented an explicit solution for infinite-depth, irrotational, two-dimensional, free-surface, attached flow past an inclined flat plate in the limit of large Froude number. The flow patterns are described by two quantities, the angle of attack ![]() $-\alpha$, and the depth of midpoint submergence
$-\alpha$, and the depth of midpoint submergence ![]() $h$, with the solution parameters determined as the simultaneous roots of four real nonlinear algebraic equations arising from the flow normalisation. This explicit form allows accurate evaluation of various flow quantities, and these are related to the large-Froude-number results of SW20 obtained by a numerical integral equation method.
$h$, with the solution parameters determined as the simultaneous roots of four real nonlinear algebraic equations arising from the flow normalisation. This explicit form allows accurate evaluation of various flow quantities, and these are related to the large-Froude-number results of SW20 obtained by a numerical integral equation method.
The minimum computation required to obtain the lift coefficient and reproduce the examples presented in § 6 consists of choosing ![]() $\alpha$ and
$\alpha$ and ![]() $h$, and then solving simultaneously the four equations (3.49)–(3.52) for the four real numbers
$h$, and then solving simultaneously the four equations (3.49)–(3.52) for the four real numbers ![]() $\arg \{\zeta _1\}$,
$\arg \{\zeta _1\}$, ![]() $\arg \{\zeta _2\}$,
$\arg \{\zeta _2\}$, ![]() $q$ and
$q$ and ![]() $\arg \{\zeta _c\}$, implementing the functions
$\arg \{\zeta _c\}$, implementing the functions ![]() $P(\zeta,q)$,
$P(\zeta,q)$, ![]() $K(\zeta,q)$ and
$K(\zeta,q)$ and ![]() $L(\zeta,q)$ using the expressions (3.5), (3.8) and (3.11). The values of
$L(\zeta,q)$ using the expressions (3.5), (3.8) and (3.11). The values of ![]() $\beta _2$ and hence
$\beta _2$ and hence ![]() $C_L$ are then given by (A7), (4.9) and (4.10).
$C_L$ are then given by (A7), (4.9) and (4.10).
The most significant approximation here is the assumption of large Froude number. The results in SW20 for flow past a cylinder at ![]() $Fr=5$ show that surface waves are absent at sufficiently large submergence and for sufficiently small submergence. The explicit results here may thus be of relevance at moderate Froude numbers at some shallow submergences. This is further borne out by the comparison in figure 9(b) of values of the lift coefficient
$Fr=5$ show that surface waves are absent at sufficiently large submergence and for sufficiently small submergence. The explicit results here may thus be of relevance at moderate Froude numbers at some shallow submergences. This is further borne out by the comparison in figure 9(b) of values of the lift coefficient ![]() $C_L$ here and those in SW20 for
$C_L$ here and those in SW20 for ![]() $ {\textit {Fr}}\geq 5$. The general similarity across all submergences suggests that at these Froude numbers, the presence of surface waves has little effect on lift, though, of course, introducing drag.
$ {\textit {Fr}}\geq 5$. The general similarity across all submergences suggests that at these Froude numbers, the presence of surface waves has little effect on lift, though, of course, introducing drag.
The Kutta condition for smoothly detaching flow introduces circulation into the flow, and consequently the free surface diverges logarithmically upwards or downwards, depending on the sign of the circulation, at large distances. It could be expected that in finite-depth flows, the free surface would become flat over horizontal distances comparable to the fluid depth, and preliminary analysis, to be presented elsewhere, shows this to indeed be the case. The methodology of Crowdy & Green (Reference Crowdy and Green2011) allows the present results to be extended also to flows periodic in the streamwise direction.
The solutions presented here are valid for arbitrary angles of attack and submergences, but are unlikely to be observed at large angles of attack when flows are likely to display separation, cavitation or ventilation, and three-dimensional and viscous effects as described in review articles and texts including, for example, Acosta (Reference Acosta1973), Faltinsen (Reference Faltinsen2005) and Molland & Turnock (Reference Molland and Turnock2022). Within the context of the present model, the solution branch could bifurcate to give multiple solutions for the same external parameters as in the vortex streets of Crowdy & Green (Reference Crowdy and Green2011).
Acknowledgements
The authors are grateful to Dr Y.A. Semenov for providing the raw data from figure 12 of SW20, plotted in figure 9 here, and to referees for helpful presentational suggestions.
Funding
E.R.J. would like to thank the Isaac Newton Institute for Mathematical Sciences for support and hospitality during the programme ‘Dispersive hydrodynamics’ when some of the work on this paper was undertaken, supported by EPSRC grant no. EP/R014604/1.
Declaration of interests
The authors report no conflict of interest.
Appendix A. Determining  $\beta _0,\ldots,\beta _5$
$\beta _0,\ldots,\beta _5$
First, recalling (3.22) and (3.29), as well as (3.8) and (3.11), one finds by comparing the coefficients of ![]() $(\zeta +\mathrm {i})^{-2}$ and
$(\zeta +\mathrm {i})^{-2}$ and ![]() $(\zeta +\mathrm {i})^{-1}$ in the Laurent series expansions of the right-hand sides of (3.40) and (3.42) about
$(\zeta +\mathrm {i})^{-1}$ in the Laurent series expansions of the right-hand sides of (3.40) and (3.42) about ![]() $\zeta =-\mathrm {i}$, that
$\zeta =-\mathrm {i}$, that
and
Relation (A1) is to be expected, given our assumption of (3.1).
Similarly, by comparing the Laurent series expansions of the right-hand sides of (3.40) and (3.42) about ![]() $\zeta =-\mathrm {i}/q^2$, one finds that
$\zeta =-\mathrm {i}/q^2$, one finds that
and
But it follows from (3.32) and (3.29) that ![]() $\varOmega (-\mathrm {i}/q^2)=\mathrm {e}^{-2\mathrm {i}\alpha }\,U$, and hence from (A3) that
$\varOmega (-\mathrm {i}/q^2)=\mathrm {e}^{-2\mathrm {i}\alpha }\,U$, and hence from (A3) that
Also, it follows from (3.34) and (3.38b) that
Then, using (A6) and recalling (3.38a) (and also (3.12b)), it follows from (A2) that
Next, by differentiating both sides of (3.32) and then setting ![]() $\zeta =-\mathrm {i}/q^2$ in the resulting equation, one can show that
$\zeta =-\mathrm {i}/q^2$ in the resulting equation, one can show that
It then follows from (A4) and (A2) that
Also, in order for ![]() $H(\zeta )$ as given by (3.42) to satisfy (3.41), it follows from (3.9a) and (3.12a) that
$H(\zeta )$ as given by (3.42) to satisfy (3.41), it follows from (3.9a) and (3.12a) that
It then follows from (A10) and (A9) that
Now, it follows from (3.40), and the properties of ![]() $W'(\zeta )$ and
$W'(\zeta )$ and ![]() $\varOmega (\zeta )$, that
$\varOmega (\zeta )$, that ![]() $H(\zeta )$ has a (simple) zero at
$H(\zeta )$ has a (simple) zero at ![]() $\zeta =\zeta _1$. Then, setting
$\zeta =\zeta _1$. Then, setting ![]() $\zeta =\zeta _1$ in (3.42) and using the fact that
$\zeta =\zeta _1$ in (3.42) and using the fact that ![]() $K(q^2,q^2)=0$ (see just after (3.35)) as well as (A1), (A5) and (A9), it follows that
$K(q^2,q^2)=0$ (see just after (3.35)) as well as (A1), (A5) and (A9), it follows that
So, in summary, the coefficients ![]() $\beta _0,\dots,\beta _5$ are given by (A12), (A11), (A7), (A9), (A1) and (A5), respectively.
$\beta _0,\dots,\beta _5$ are given by (A12), (A11), (A7), (A9), (A1) and (A5), respectively.
Finally, we make the following observation about ![]() $\beta _2$ that we make use of in §§ 3.6 and 4. By differentiating both sides of (3.30) with respect to
$\beta _2$ that we make use of in §§ 3.6 and 4. By differentiating both sides of (3.30) with respect to ![]() $\zeta$ and then setting
$\zeta$ and then setting ![]() $\zeta =-\mathrm {i}$ in the resulting equation, and also recalling (3.29), one can show that
$\zeta =-\mathrm {i}$ in the resulting equation, and also recalling (3.29), one can show that ![]() $\overline {\varOmega '(-\mathrm {i})}=-\varOmega '(-\mathrm {i})$, i.e. that
$\overline {\varOmega '(-\mathrm {i})}=-\varOmega '(-\mathrm {i})$, i.e. that ![]() $\varOmega '(-\mathrm {i})$ is purely imaginary. It then follows from (A2) that
$\varOmega '(-\mathrm {i})$ is purely imaginary. It then follows from (A2) that ![]() $\beta _2$ is purely imaginary.
$\beta _2$ is purely imaginary.
Appendix B. Determining the sum  $\gamma _0+\gamma _1$
$\gamma _0+\gamma _1$
First, we note that it follows from (4.3), and the properties of ![]() $W'(\zeta )$ and
$W'(\zeta )$ and ![]() $\varOmega (\zeta )$, that
$\varOmega (\zeta )$, that ![]() $\eta (\zeta )$ has a (simple) zero at
$\eta (\zeta )$ has a (simple) zero at ![]() $\zeta =1/\overline {\zeta _1}$. Then, setting
$\zeta =1/\overline {\zeta _1}$. Then, setting ![]() $\zeta =1/\overline {\zeta _1}$ in (4.5), and using the fact that
$\zeta =1/\overline {\zeta _1}$ in (4.5), and using the fact that ![]() $K(1/q^2,q^2)=1$ (which follows from the fact that
$K(1/q^2,q^2)=1$ (which follows from the fact that ![]() $K(q^2,q^2)=0$ – see just after (3.35) – and (3.9a)), and recalling that
$K(q^2,q^2)=0$ – see just after (3.35) – and (3.9a)), and recalling that ![]() $1/\overline {\zeta _1}=\zeta _1/q^2$ as well as (3.9a) and (3.12a), it follows that
$1/\overline {\zeta _1}=\zeta _1/q^2$ as well as (3.9a) and (3.12a), it follows that
Next, one can determine the constants ![]() $\gamma _2,\ldots \gamma _5$ in a manner similar to how we determined the constants
$\gamma _2,\ldots \gamma _5$ in a manner similar to how we determined the constants ![]() $\beta _0,\ldots \beta _5$ in Appendix A. That is, by comparing coefficients of the Laurent series expansions of the right-hand sides of (4.3) and (4.5) about
$\beta _0,\ldots \beta _5$ in Appendix A. That is, by comparing coefficients of the Laurent series expansions of the right-hand sides of (4.3) and (4.5) about ![]() $\zeta =-\mathrm {i}$ and
$\zeta =-\mathrm {i}$ and ![]() $\zeta =-\mathrm {i}/q^2$, whilst also recalling (A2), (A4), (A9) as well as the fact that
$\zeta =-\mathrm {i}/q^2$, whilst also recalling (A2), (A4), (A9) as well as the fact that ![]() $\varOmega (-\mathrm {i}/q^2)=\mathrm {e}^{-2\mathrm {i}\alpha }\,U$ (see just after (A4)), one finds that
$\varOmega (-\mathrm {i}/q^2)=\mathrm {e}^{-2\mathrm {i}\alpha }\,U$ (see just after (A4)), one finds that
Then, substituting for ![]() $\gamma _2,\ldots,\gamma _5$ in (B1) with (B2a–d), and also recalling (A12) and the requirement (3.45), one finds that
$\gamma _2,\ldots,\gamma _5$ in (B1) with (B2a–d), and also recalling (A12) and the requirement (3.45), one finds that