Article contents
The history force on a small particle in a linearly stratified fluid
Published online by Cambridge University Press: 15 May 2014
Abstract
The hydrodynamic force experienced by a small spherical particle undergoing an arbitrary time-dependent motion in a weakly density-stratified fluid is investigated theoretically. The study is carried out under the Oberbeck–Boussinesq approximation and in the limit of small Reynolds and small Péclet numbers. The force acting on the particle is obtained by using matched-asymptotic expansions. In this approach, the small parameter is given by 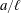 $a/\ell $ , where
$a/\ell $ , where  $a$ is the particle radius and
$a$ is the particle radius and 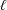 $\ell $ is the stratification length, as defined by Ardekani & Stocker (Phys. Rev. Lett., vol. 105, 2010, article 084502), which depends on the Brunt–Väisälä frequency, on the fluid kinematic viscosity and on the thermal or the concentration diffusivity (depending on the case considered). The matching procedure used here, which is based on series expansions of generalized functions, slightly differs from that generally used in similar problems. In addition to the classical Stokes drag, it is found that the particle experiences a memory force given by two convolution products, one of which involves, as usual, the particle acceleration and the other one, the particle velocity. Owing to the stratification, the transient behaviour of this memory force, in response to an abrupt motion, consists of an initial fast decrease followed by a damped oscillation with an angular frequency corresponding to the Brunt–Väisälä frequency. The perturbation force eventually tends to a constant which provides us with correction terms that should be added to the Stokes drag to accurately predict the settling time of a particle in a diffusive stratified fluid.
$\ell $ is the stratification length, as defined by Ardekani & Stocker (Phys. Rev. Lett., vol. 105, 2010, article 084502), which depends on the Brunt–Väisälä frequency, on the fluid kinematic viscosity and on the thermal or the concentration diffusivity (depending on the case considered). The matching procedure used here, which is based on series expansions of generalized functions, slightly differs from that generally used in similar problems. In addition to the classical Stokes drag, it is found that the particle experiences a memory force given by two convolution products, one of which involves, as usual, the particle acceleration and the other one, the particle velocity. Owing to the stratification, the transient behaviour of this memory force, in response to an abrupt motion, consists of an initial fast decrease followed by a damped oscillation with an angular frequency corresponding to the Brunt–Väisälä frequency. The perturbation force eventually tends to a constant which provides us with correction terms that should be added to the Stokes drag to accurately predict the settling time of a particle in a diffusive stratified fluid.
Information
- Type
- Papers
- Information
- Copyright
- © 2014 Cambridge University Press
References
- 27
- Cited by

