Hostname: page-component-76c49bb84f-bg8zk Total loading time: 0 Render date: 2025-07-10T01:33:48.267Z Has data issue: false hasContentIssue false
  • English
  • Français

How can two circular self-propelled particles form a stable wedge-like conformation in channel flow?

Published online by Cambridge University Press:  03 July 2025

Lizhong Huang Open the ORCID record for Lizhong Huang [Opens in a new window] ,
Jianzhong Lin Open the ORCID record for Jianzhong Lin [Opens in a new window] ,
Ruijin Wang Open the ORCID record for Ruijin Wang [Opens in a new window] ,
Yang Li Open the ORCID record for Yang Li [Opens in a new window] ,
Xiao Jin Open the ORCID record for Xiao Jin [Opens in a new window]  and
Chun Shao Open the ORCID record for Chun Shao [Opens in a new window]
Lizhong Huang
Affiliation:
School of Mechanical Engineering, Hangzhou Dianzi University, Hangzhou 310018, PR China
Jianzhong Lin*
Affiliation:
Zhejiang Provincial Engineering Research Center for the Safety of Pressure Vessel and Pipeline, Ningbo University, Ningbo 315201, PR China State Key Laboratory of Fluid Power Transmission and Control, Zhejiang University, Hangzhou 310027, PR China
Ruijin Wang
Affiliation:
School of Mechanical Engineering, Hangzhou Dianzi University, Hangzhou 310018, PR China
Yang Li
Affiliation:
School of Mechanical Engineering, Hangzhou Dianzi University, Hangzhou 310018, PR China
Xiao Jin
Affiliation:
School of Mechanical Engineering, Hangzhou Dianzi University, Hangzhou 310018, PR China
Chun Shao
Affiliation:
School of Mechanical Engineering, Hangzhou Dianzi University, Hangzhou 310018, PR China
*
Corresponding author: Jianzhong Lin, mecjzlin@public.zju.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

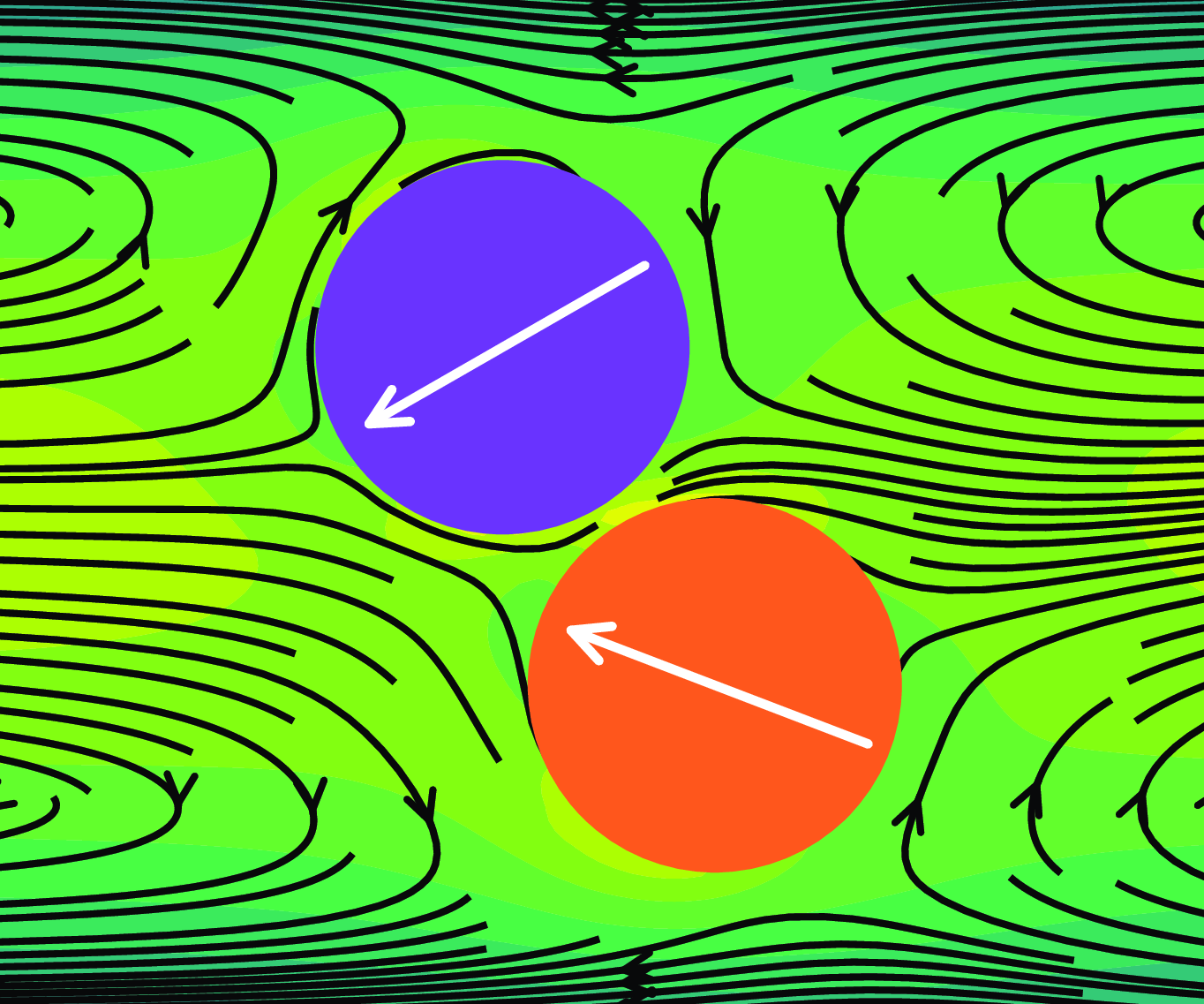
We investigate the dynamics of circular self-propelled particles in channel flow, modelled as squirmers using a two-dimensional lattice Boltzmann method. The simulations explore a wide range of parameters, including channel Reynolds numbers ($\textit{Re}_c$), squirmer Reynolds numbers ($\textit{Re}_s$) and squirmer-type factors ($\beta$). For a single squirmer, four motion regimes are identified: oscillatory motion confined to one side of the channel, oscillatory crossing of the channel centreline, stabilisation at a lateral equilibrium position with the squirmer tilted and stable upstream swimming near the channel centreline. For two squirmers, interactions produce not only these four corresponding regimes but also three additional ones: continuous collisions with repeated position exchanges, progressive separation and drifting apart and, most notably, the formation of a stable wedge-like conformation (regime D). A key finding is the emergence of regime D, which predominantly occurs for weak pullers ($\beta = 1$) and at moderate to high $\textit{Re}_c$ values. Hydrodynamic interactions align the squirmers with streamline bifurcations near the channel centreline, enabling stability despite transient oscillations. Additionally, the channel blockage ratio critically affects the range of $\textit{Re}_s$ values over which this regime occurs, highlighting the influence of geometric confinement. This study extends the understanding of squirmer dynamics, revealing how hydrodynamic interactions drive collective behaviours. The findings also offer insights into the design of self-propelled particles for biomedical applications and contribute to the theoretical framework for active matter systems. Future work will investigate three-dimensional effects and the stability conditions for spherical squirmers forming stable wedge-like conformations, further generalising these results.

JFM classification

Biological Fluid Dynamics: Micro-organism dynamics Complex Fluids: Active matter Multiphase and Particle-laden Flows: Particle/fluid flow

Information

Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 1014 , 10 July 2025 , A19
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Aidun, C.K., Lu, Y. & Ding, E.J. 1998 Direct analysis of particulate suspensions with inertia using the discrete Boltzmann equation. J. Fluid Mech. 373, 287–311.10.1017/S0022112098002493CrossRefGoogle Scholar
Alapan, Y., Yasa, O., Schauer, O., Giltinan, J., Tabak, A.F., Sourjik, V. & Sitti, M. 2018 Soft erythrocyte-based bacterial microswimmers for cargo delivery. Sci. Robot. 3 (17), eaar4423.10.1126/scirobotics.aar4423CrossRefGoogle ScholarPubMed
Blake, J.R. 1971 a Self propulsion due to oscillations on the surface of a cylinder at low Reynolds number. Bull. Austral. Math. Soc. 5 (2), 255–264.CrossRefGoogle Scholar
Blake, J.R. 1971 b A spherical envelope approach to ciliary propulsion. J. Fluid Mech. 46 (1), 199–208.10.1017/S002211207100048XCrossRefGoogle Scholar
Chisholm, N.G., Legendre, D., Lauga, E. & Khair, A.S. 2016 A squirmer across Reynolds numbers. J. Fluid Mech. 796, 233–256.CrossRefGoogle Scholar
Choudhary, A., Paul, S., Rühle, F. & Stark, H. 2022 How inertial lift affects the dynamics of a microswimmer in Poiseuille flow. Commun. Phys. 5 (1), 14.CrossRefGoogle Scholar
Dey, R., Buness, C.M., Hokmabad, B.V., Jin, C. & Maass, C.C. 2022 Oscillatory rheotaxis of artificial swimmers in microchannels. Nat. Commun. 13 (1), 2952.CrossRefGoogle ScholarPubMed
Drescher, K., Leptos, K.C., Tuval, I., Ishikawa, T., Pedley, T.J. & Goldstein, R.E. 2009 Dancing Volvox: hydrodynamic bound states of swimming algae. Phys. Rev. Lett. 102 (16), 168101.CrossRefGoogle ScholarPubMed
Elgeti, J., Winkler, R.G. & Gompper, G. 2015 Physics of microswimmers—single particle motion and collective behavior: a review. Rep. Prog. Phys. 78 (5), 056601.CrossRefGoogle ScholarPubMed
Fadda, F., Molina, J.J. & Yamamoto, R. 2020 Dynamics of a chiral swimmer sedimenting on a flat plate. Phys. Rev. E 101 (5), 052608.10.1103/PhysRevE.101.052608CrossRefGoogle ScholarPubMed
Feng, Z.G. & Michaelides, E.E. 2004 The immersed boundary-lattice Boltzmann method for solving fluid–particles interaction problems. J. Comput. Phys. 195 (2), 602–628.10.1016/j.jcp.2003.10.013CrossRefGoogle Scholar
Glowinski, R., Pan, T.W., Hesla, T.I., Joseph, D.D. & Periaux, J. 2001 A fictitious domain approach to the direct numerical simulation of incompressible viscous flow past moving rigid bodies: application to particulate flow. J. Comput. Phys. 169 (2), 363–426.10.1006/jcph.2000.6542CrossRefGoogle Scholar
Guan, G. & Lin, J. 2023 Study on the interaction and motion patterns of squirmers swimming in a shear flow. Phys. Fluids 35 (6), 063302.Google Scholar
Guan, G., Ying, Y. & Lin, J. 2024 Effect of the shape of microswimmers and slip boundary conditions on the dynamic characteristics of near-wall microswimmers. J. Fluid Mech. 999, A42.CrossRefGoogle Scholar
He, X. & Luo, L.S. 1997 Lattice Boltzmann model for the incompressible Navier–Stokes equation. J. Stat. Phys. 88 (3-4), 927–944.10.1023/B:JOSS.0000015179.12689.e4CrossRefGoogle Scholar
Huang, L., Du, J. & Zhu, Z. 2021 Neutrally buoyant particle migration in Poiseuille flow driven by pulsatile velocity. Micromachines-BASEL 12 (9), 1075.CrossRefGoogle ScholarPubMed
Ishikawa, T. 2024 Fluid dynamics of squirmers and ciliated microorganisms. Annu. Rev. Fluid Mech. 56 (1), 119–145.CrossRefGoogle Scholar
Ishikawa, T., Brumley, D.R. & Pedley, T.J. 2021 Rheology of a concentrated suspension of spherical squirmers: monolayer in simple shear flow. J. Fluid Mech. 914, A26.CrossRefGoogle Scholar
Ishikawa, T. & Hota, M. 2006 Interaction of two swimming Paramecia . J. Expl Biol. 209 (22), 4452–4463.CrossRefGoogle ScholarPubMed
Ishikawa, T., Sekiya, G., Imai, Y. & Yamaguchi, T. 2007 Hydrodynamic interactions between two swimming bacteria. Biophys. J. 93 (6), 2217–2225.CrossRefGoogle ScholarPubMed
Ishikawa, T., Simmonds, M.P. & Pedley, T.J. 2006 Hydrodynamic interaction of two swimming model micro-organisms. J. Fluid Mech. 568, 119–160.10.1017/S0022112006002631CrossRefGoogle Scholar
Ishimoto, K. 2017 Guidance of microswimmers by wall and flow: thigmotaxis and rheotaxis of unsteady squirmers in two and three dimensions. Phys. Rev. E 96 (4), 043103.10.1103/PhysRevE.96.043103CrossRefGoogle Scholar
Ito, H., Omori, T. & Ishikawa, T. 2019 Swimming mediated by ciliary beating: comparison with a squirmer model. J. Fluid Mech. 874, 774–796.10.1017/jfm.2019.490CrossRefGoogle Scholar
Jafari, S., Yamamoto, R. & Rahnama, M. 2011 Lattice-Boltzmann method combined with smoothed-profile method for particulate suspensions. Phys. Rev. E 83 (2), 026702.10.1103/PhysRevE.83.026702CrossRefGoogle ScholarPubMed
Koch, D.L. & Subramanian, G. 2011 Collective hydrodynamics of swimming microorganisms: living fluids. Annu. Rev. Fluid Mech. 43 (1), 637–659.10.1146/annurev-fluid-121108-145434CrossRefGoogle Scholar
Kong, X., Gao, P., Wang, J., Fang, Y. & Hwang, K.C. 2023 Advances of medical nanorobots for future cancer treatments. J. Hematol. Oncol. 16 (1), 74.10.1186/s13045-023-01463-zCrossRefGoogle ScholarPubMed
Kuron, M., Stärk, P., Burkard, C., De Graaf, J. & Holm, C. 2019 A lattice Boltzmann model for squirmers. J. Chem. Phys. 150 (14), 144110.CrossRefGoogle ScholarPubMed
Lallemand, P. & Luo, L.S. 2003 Lattice Boltzmann method for moving boundaries. J. Comput. Phys. 184 (2), 406–421.CrossRefGoogle Scholar
Lauga, E. 2016 Bacterial hydrodynamics. Annu. Rev. Fluid Mech. 48 (1), 105–130.10.1146/annurev-fluid-122414-034606CrossRefGoogle Scholar
Lauga, E. & Powers, T.R. 2009 The hydrodynamics of swimming microorganisms. Rep. Prog. Phys. 72 (9), 096601.CrossRefGoogle Scholar
Li, G., Ostace, A. & Ardekani, A.M. 2016 Hydrodynamic interaction of swimming organisms in an inertial regime. Phys. Rev. E 94 (5), 053104.10.1103/PhysRevE.94.053104CrossRefGoogle Scholar
Li, S. & Nie, D. 2024 Study on the effect of geometric shape on microswimmer upstream motion. Phys. Fluids 36 (10), 103351.CrossRefGoogle Scholar
Li, Z. et al. 2024 Biohybrid microrobots regulate colonic cytokines and the epithelium barrier in inflammatory bowel disease. Sci. Robot. 9 (91), eadl2007.CrossRefGoogle ScholarPubMed
Lighthill, M.J. 1952 On the squirming motion of nearly spherical deformable bodies through liquids at very small Reynolds numbers. Commun. Pure Appl. Maths 5 (2), 109–118.10.1002/cpa.3160050201CrossRefGoogle Scholar
More, R.V. & Ardekani, A.M. 2021 Hydrodynamic interactions between swimming microorganisms in a linearly density stratified fluid. Phys. Rev. E 103 (1), 013109.10.1103/PhysRevE.103.013109CrossRefGoogle Scholar
Nie, D., Ying, Y., Guan, G., Lin, J. & Ouyang, Z. 2023 Two-dimensional study on the motion and interactions of squirmers under gravity in a vertical channel. J. Fluid Mech. 960, A31.10.1017/jfm.2023.155CrossRefGoogle Scholar
Omori, T., Kikuchi, K., Schmitz, M., Pavlovic, M., Chuang, C.H. & Ishikawa, T. 2022 Rheotaxis and migration of an unsteady microswimmer. J. Fluid Mech. 930, A30.10.1017/jfm.2021.921CrossRefGoogle Scholar
Ouyang, Z. & Lin, J. 2021 Migration of a micro-swimmer in a channel flow. Powder Technol. 392, 587–600.10.1016/j.powtec.2021.07.027CrossRefGoogle Scholar
Ouyang, Z. & Lin, J. 2022 Behaviors of a settling microswimmer in a narrow vertical channel. Powder Technol. 398, 117042.CrossRefGoogle Scholar
Papavassiliou, D. & Alexander, G.P. 2017 Exact solutions for hydrodynamic interactions of two squirming spheres. J. Fluid Mech. 813, 618–646.CrossRefGoogle Scholar
Polin, M., Tuval, I., Drescher, K., Gollub, J.P. & Goldstein, R.E. 2009 Chlamydomonas swims with two ‘gears’ in a eukaryotic version of run-and-tumble locomotion. Science 325 (5939), 487–490.10.1126/science.1172667CrossRefGoogle Scholar
Pooley, C.M., Alexander, G.P. & Yeomans, J.M. 2007 Hydrodynamic interaction between two swimmers at low Reynolds number. Phys. Rev. Lett. 99 (22), 228103.CrossRefGoogle ScholarPubMed
Purushothaman, A. & Thampi, S.P. 2019 Confinement induced trajectory of a squirmer in a two dimensional channel. Fluid Dyn. Res. 51 (6), 065504.Google Scholar
Purushothaman, A. & Thampi, S.P. 2021 Hydrodynamic collision between a microswimmer and a passive particle in a micro-channel. Soft Matt. 17 (12), 3380–3396.10.1039/D0SM02140GCrossRefGoogle Scholar
Qi, K., Westphal, E., Gompper, G. & Winkler, R.G. 2022 Emergence of active turbulence in microswimmer suspensions due to active hydrodynamic stress and volume exclusion. Commun. Phys. 5 (1), 49.CrossRefGoogle Scholar
Qian, Y.H., d’Humières, D. & Lallemand, P. 1992 Lattice BGK models for Navier–Stokes equation. Europhys.Lett. 17 (6), 479–484.10.1209/0295-5075/17/6/001CrossRefGoogle Scholar
Radhakrishnan, B.N., Purushothaman, A., Dey, R. & Thampi, S.P. 2024 Confinement induced three-dimensional trajectories of microswimmers in rectangular channels. Phys. Rev. Fluids 9 (8), 083302.10.1103/PhysRevFluids.9.083302CrossRefGoogle Scholar
Rühle, F., Blaschke, J., Kuhr, J.T. & Stark, H. 2018 Gravity-induced dynamics of a squirmer microswimmer in wall proximity. New J. Phys. 20 (2), 025003.10.1088/1367-2630/aa9ed3CrossRefGoogle Scholar
Theers, M., Westphal, E., Gompper, G. & Winkler, R.G. 2016 Modeling a spheroidal microswimmer and cooperative swimming in a narrow slit. Soft Matt. 12 (35), 7372–7385.CrossRefGoogle ScholarPubMed
Theers, M., Westphal, E., Qi, K., Winkler, R.G. & Gompper, G. 2018 Clustering of microswimmers: interplay of shape and hydrodynamics. Soft Matt. 14 (42), 8590–8603.10.1039/C8SM01390JCrossRefGoogle ScholarPubMed
Wan, D. & Turek, S. 2006 Direct numerical simulation of particulate flow via multigrid FEM techniques and the fictitious boundary method. Intl J. Numer. Meth. Fluids 51 (5), 531–566.10.1002/fld.1129CrossRefGoogle Scholar
Wen, B., Li, H., Zhang, C. & Fang, H. 2012 Lattice-type-dependent momentum-exchange method for moving boundaries. Phys. Rev. E 85 (1), 016704.CrossRefGoogle ScholarPubMed
Wu, J. & Shu, C. 2010 Particulate flow simulation via a boundary condition-enforced immersed boundary-lattice Boltzmann scheme. Commun. Comput. Phys. 7 (4), 793–812.Google Scholar
Ying, Y., Jiang, T., Nie, D. & Lin, J. 2022 Study on the sedimentation and interaction of two squirmers in a vertical channel. Phys. Fluids 34 (10), 103315.10.1063/5.0107133CrossRefGoogle Scholar
Zhang, F. et al. 2024 Biohybrid microrobots locally and actively deliver drug-loaded nanoparticles to inhibit the progression of lung metastasis. Sci. Adv. 10 (24), eadn6157.10.1126/sciadv.adn6157CrossRefGoogle ScholarPubMed
Zhang, F. et al. 2021 ACE2 receptor-modified algae-based microrobot for removal of SARS-CoV-2 in wastewater. J. Am. Chem. Soc. 143 (31), 12194–12201.CrossRefGoogle ScholarPubMed
Zöttl, A. & Stark, H. 2012 Nonlinear dynamics of a microswimmer in Poiseuille flow. Phys. Rev. Lett. 108 (21), 218104.CrossRefGoogle ScholarPubMed
Zöttl, A. & Stark, H. 2023 Modeling active colloids: from active Brownian particles to hydrodynamic and chemical fields. Annu. Rev. Condens. Matter Phys. 14 (1), 109–127.10.1146/annurev-conmatphys-040821-115500CrossRefGoogle Scholar
Supplementary material: File

Huang et al. supplementary material movie 1

Time evolution of a single squirmer in Regime I ( $Re_s = 0.5$, $Re_c = 5$, $\\beta = -5$ ), exhibiting downstream oscillations within the lower half of the channel.
Download Huang et al. supplementary material movie 1(File)
File 7.4 MB
Supplementary material: File

Huang et al. supplementary material movie 2

Time evolution of a single squirmer in Regime II ( $Re_s = 0.5$, $Re_c = 20$, $\\beta = 5$ ), exhibiting periodic oscillations that cross the channel centerline.
Download Huang et al. supplementary material movie 2(File)
File 2.9 MB
Supplementary material: File

Huang et al. supplementary material movie 3

Time evolution of a single squirmer in Regime III ( $Re_s = 0.5$, $Re_c = 20$, $\\beta = -5$ ), exhibiting stable upstream swimming at a lateral equilibrium position.
Download Huang et al. supplementary material movie 3(File)
File 2.4 MB
Supplementary material: File

Huang et al. supplementary material movie 4

Time evolution of a single squirmer in Regime IV ( $Re_s = 1.0$, $Re_c = 5$, $\\beta = 3$ ), exhibiting stabilization near the channel centerline with minimal oscillations.
Download Huang et al. supplementary material movie 4(File)
File 2.7 MB
Supplementary material: File

Huang et al. supplementary material movie 5

Time evolution of two squirmers in Regime A ( $Re_s = 0.5$, $Re_c = 5$, $\\beta = -5$ ), exhibiting oscillations within one half of the channel, either together or in opposite halves of the channel.
Download Huang et al. supplementary material movie 5(File)
File 1.7 MB
Supplementary material: File

Huang et al. supplementary material movie 6

Time evolution of two squirmers in Regime B ( $Re_s = 0.5$, $Re_c = 20$, $\\beta = 5$ ), exhibiting oscillatory motion spanning the channel centerline.
Download Huang et al. supplementary material movie 6(File)
File 838 KB
Supplementary material: File

Huang et al. supplementary material movie 7

Time evolution of two squirmers in Regime C ( $Re_s = 0.5$, $Re_c = 20$, $\\beta = -5$ ), exhibiting stabilization at lateral equilibrium within one half of the channel with a tilted swimming orientation.
Download Huang et al. supplementary material movie 7(File)
File 4.2 MB
Supplementary material: File

Huang et al. supplementary material movie 8

Time evolution of two squirmers in Regime D ( $Re_s = 0.5$, $Re_c = 20$, $\\beta = 1$ ), exhibiting eventual stabilization into a wedge-like conformation.
Download Huang et al. supplementary material movie 8(File)
File 6.1 MB
Supplementary material: File

Huang et al. supplementary material movie 9

Time evolution of two squirmers in Regime E ( $Re_s = 2.0$, $Re_c = 5$, $\\beta = 0$ ), exhibiting upstream stabilization near the channel centerline.
Download Huang et al. supplementary material movie 9(File)
File 2.9 MB
Supplementary material: File

Huang et al. supplementary material movie 10

Time evolution of two squirmers in Regime F ( $Re_s = 1.0$, $Re_c = 10$, $\\beta = 3$ ), exhibiting repeated collisions with occasional position exchanges.
Download Huang et al. supplementary material movie 10(File)
File 7.2 MB
Supplementary material: File

Huang et al. supplementary material movie 11

Time evolution of two squirmers in Regime G ( $Re_s = 1.0$, $Re_c = 5$, $\\beta = 3$ ), exhibiting progressive drift apart and eventual exit from the simulation domain.
Download Huang et al. supplementary material movie 11(File)
File 1.5 MB