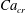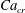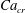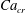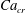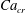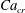1 Introduction
Emulsions, which consist of droplets of one fluid dispersed in another fluid, are common in our daily lives and can be found in the production processes of food, personal care products and pharmaceuticals (Sjöblom Reference Sjöblom2005; Seemann et al. Reference Seemann, Brinkmann, Pfohl and Herminghaus2011). Since emulsion properties such as the stability, rheology and particle morphology are heavily dependent on the droplet size distribution, it is of great importance to control the droplet deformation, breakup and coalescence during emulsification. Once the emulsification device and the compositions of emulsions have been determined, the control of droplet dynamics can be realized through the addition of surfactants (Kobayashi et al. Reference Kobayashi, Nakajima, Chun, Kikuchi and Fujita2002; Kobayashi, Nakajima & Mukataka Reference Kobayashi, Nakajima and Mukataka2003; Kobayashi, Mukataka & Nakajima Reference Kobayashi, Mukataka and Nakajima2005; Van der Graaf et al. Reference Van der Graaf, Steegmans, Van der Sman, Schroën and Boom2005; Kobayashi et al. Reference Kobayashi, Takano, Maeda, Wada, Uemura and Nakajima2008; Chen et al. Reference Chen, Liu, Xu and Luo2015; Josephides & Sajjadi Reference Josephides and Sajjadi2015).
In the investigation of droplet dynamics, numerical simulation is playing an increasingly important role, as it can provide easier access to quantities such as droplet deformation and orientation as well as the velocity, pressure and surfactant concentration distributions inside and outside the droplet, which are difficult to measure experimentally. However, the efficient and accurate computational modelling of droplet dynamics with surfactants in a multiphase system remains a challenging task. The surfactant concentration at the interface alters the interfacial tension locally. The non-uniform surfactant concentration creates non-uniform interfacial tension forces and Marangoni stresses along the interface, which in turn affect the flow field in a complicated manner. Meanwhile, the flow field will influence the surfactant distribution. The interaction between surfactants and the flow field is highly nonlinear. Numerically, the surfactant evolution equation must be solved together with the hydrodynamic equations on moving and deforming interfaces that may undergo topological changes such as breakup and coalescence. In addition, for soluble surfactants, they are not only able to convect and diffuse along the interface, but also to be adsorbed to or desorbed from the interface. The exchange of surfactants between the interface and the bulk phase further increases the computational complexity.
Numerical methods to simulate interfacial flows with surfactants based on conventional Navier–Stokes solvers can roughly be divided into two categories: interface-tracking and interface-capturing methods. Interface-tracking methods, including mainly the boundary integral method (BIM) (Stone Reference Stone1990; Stone & Leal Reference Stone and Leal1990; Milliken & Leal Reference Milliken and Leal1994; Stone Reference Stone1994; Eggleton, Pawar & Stebe Reference Eggleton, Pawar and Stebe1999; Johnson & Borhan Reference Johnson and Borhan2000; Eggleton, Tsai & Stebe Reference Eggleton, Tsai and Stebe2001; Kruijt-Stegeman, van de Vosse & Meijer Reference Kruijt-Stegeman, van de Vosse and Meijer2004; Bazhlekov, Anderson & Meijer Reference Bazhlekov, Anderson and Meijer2006; Feigl et al. Reference Feigl, Megias-Alguacil, Fischer and Windhab2007), the front-tracking method (Zhang, Eckmann & Ayyaswamy Reference Zhang, Eckmann and Ayyaswamy2006; Muradoglu & Tryggvason Reference Muradoglu and Tryggvason2008) and the immersed boundary method (Jin & Stebe Reference Jin and Stebe2007; Lai, Tseng & Huang Reference Lai, Tseng and Huang2008, Reference Lai, Tseng and Huang2010), use the Lagrangian approach to explicitly represent the interface. The BIM employs a surface mesh to track the interface. It was first proposed by Stone & Leal (Reference Stone and Leal1990) to simulate the droplet deformation with insoluble surfactants, in which the surfactant concentration was obtained by solving a time-dependent convective–diffusion equation (Stone Reference Stone1990). This method was extended to 3D flows by Bazhlekov et al. (Reference Bazhlekov, Anderson and Meijer2006) and Feigl et al. (Reference Feigl, Megias-Alguacil, Fischer and Windhab2007), and to soluble surfactants by Milliken & Leal (Reference Milliken and Leal1994). Eggleton et al. (Reference Eggleton, Pawar and Stebe1999) found that the surfactants accumulate at the droplet tips and may drive the interfacial tension to near zero, and thus they improved the BIM by accounting for the maximum limit of surfactant concentration. To date, the BIM has become the most successful method for studying the deformation of surfactant-laden droplets. Another popular interface-tracking method is the front-tracking method (Tryggvason et al. Reference Tryggvason, Bunner, Esmaeeli, Juric, Al-Rawahi, Tauber, Han, Nas and Jan2001), in which a fixed grid is used to determine the fluid flow while the interface is tracked using a lower-dimensional grid; this method for soluble surfactants was further developed by Zhang et al. (Reference Zhang, Eckmann and Ayyaswamy2006) and Muradoglu & Tryggvason (Reference Muradoglu and Tryggvason2008). The immersed boundary method for interfacial flows with insoluble surfactants was proposed by Lai et al. (Reference Lai, Tseng and Huang2008), in which a mixture of Eulerian variables in the fluid domain and Lagrangian variables represented by a set of discrete Lagrangian markers is used, and this method was later extended to contact line simulations (Lai et al. Reference Lai, Tseng and Huang2010). Although interface-tracking methods have been widely used to simulate the dynamics of surfactant-laden droplets, they have difficulty in dealing with droplets undergoing topological changes such as breakup and coalescence.
Interface-capturing methods use an indicator function to implicitly represent the interface in an Eulerian grid. This simplifies gridding, discretization and handling of topological changes. Commonly used interface-capturing methods are the volume-of-fluid method (James & Lowengrub Reference James and Lowengrub2004; Alke & Bothe Reference Alke and Bothe2009), the level-set method (Ceniceros Reference Ceniceros2003; Deng, Ito & Li Reference Deng, Ito and Li2003; Xu & Zhao Reference Xu and Zhao2003; Xu et al. Reference Xu, Li, Lowengrub and Zhao2006; Xu, Yang & Lowengrub Reference Xu, Yang and Lowengrub2012) and the phase-field method (Teigen et al. Reference Teigen, Li, Lowengrub, Wang and Voigt2009, Reference Teigen, Song, Lowengrub and Voigt2011). James & Lowengrub (Reference James and Lowengrub2004) proposed an axisymmetric volume-of-fluid method for insoluble surfactants on a moving fluid interface, in which they tracked the surfactant mass and surface area independently instead of directly solving the surfactant concentration. This model was extended to 3D flows with soluble surfactants by Alke & Bothe (Reference Alke and Bothe2009). Based on an Eulerian formulation of the surfactant concentration equation, Xu & Zhao (Reference Xu and Zhao2003) developed a level-set method for interfacial Stokes flows with insoluble surfactants, in which the surfactant concentration was extended to a neighbourhood of the interface through an additional Hamilton–Jacobian equation. This method was improved with the use of an immersed interface method for the Stokes flow field (Xu et al. Reference Xu, Li, Lowengrub and Zhao2006) and a continuum surface force model for the stress jump condition (Xu et al. Reference Xu, Yang and Lowengrub2012), and was recently extended to model contact line dynamics (Xu & Ren Reference Xu and Ren2014). Teigen et al. (Reference Teigen, Song, Lowengrub and Voigt2011) developed a phase-field method to simulate soluble surfactants, in which the interface structure was resolved via a free energy functional based on the Cahn–Hilliard theory. With the aid of a delta function, the surfactant evolution equations in the bulk phases and on the interface were extended to the entire fluid domain by incorporating additional terms to approximate the physical boundary condition at the interface. The resulting surfactant evolution equations are known as the surfactant evolution equations of diffuse-interface form in order to distinguish from their equivalence to the sharp-interface form (Xu & Zhao Reference Xu and Zhao2003). The surfactant evolution equation of diffuse-interface form does not need additional procedures to extend the surfactant concentration to a neighbourhood of the interface, greatly simplifying the modelling of surfactant dynamics. Despite their great success in simulating droplet breakup and coalescence, the volume-of-fluid and level-set methods require either sophisticated interface reconstruction algorithms or unphysical re-initialization processes to represent the interface and surfactant concentration, and the phase-field method yields an interface thickness far greater than its actual value, which may lead to unphysical dissolution of small droplets (Zhang & Wang Reference Zhang and Wang2010) and mobility-dependent numerical results (van der Sman & van der Graaf Reference van der Sman and van der Graaf2008; Magaletti et al. Reference Magaletti, Picano, Chinappi, Marino and Casciola2013). It still remains an open question for the phase-field method to choose an appropriate interface thickness so that the numerical difficulties become amenable while the correct physics can be captured.
Recently, the lattice Boltzmann (LB) method has shown great potential for modelling interfacial interactions. It is a pseudomolecular method tracking the evolution of the distribution function of an assembly of molecules and built upon microscopic models and mesoscopic kinetic equations. Its mesoscopic nature can provide many advantages of molecular dynamics, making the LB method particularly useful for simulation of multiphase multicomponent flows. A number of multiphase multicomponent models have been proposed, which can be classified into four main categories: the colour-gradient model (Gunstensen et al. Reference Gunstensen, Rothman, Zaleski and Zanetti1991; Halliday et al. Reference Halliday, Law, Care and Hollis2006; Liu, Valocchi & Kang Reference Liu, Valocchi and Kang2012a ), the phase-field-based model (Swift, Osborn & Yeomans Reference Swift, Osborn and Yeomans1995; Pooley, Kusumaatmaja & Yeomans Reference Pooley, Kusumaatmaja and Yeomans2008; Wang et al. Reference Wang, Shu, Huang and Teo2015; Kusumaatmaja, Hemingway & Fielding Reference Kusumaatmaja, Hemingway and Fielding2016), the interparticle-potential model (Shan & Chen Reference Shan and Chen1993; Benzi et al. Reference Benzi, Biferale, Sbragaglia, Succi and Toschi2006; Sbragaglia et al. Reference Sbragaglia, Benzi, Biferale, Succi, Sugiyama and Toschi2007; Falcucci et al. Reference Falcucci, Ubertini, Bella, Maio and Palpacelli2010a ; Falcucci, Ubertini & Succi Reference Falcucci, Ubertini and Succi2010b ; Falcucci et al. Reference Falcucci, Jannelli, Ubertini and Succi2013; Montessori et al. Reference Montessori, Falcucci, Rocca, Ansumali and Succi2015) and the mean-field theory model (He & Doolen Reference He and Doolen2002). Among these models, the colour-gradient model has been extensively used to simulate immiscible multiphase flow problems because of its strengths such as low spurious velocities, high numerical accuracy, strict mass conservation for each fluid and good numerical stability for a broad range of fluid properties. Recently, it was extended to model thermocapillary flows (Liu, Zhang & Valocchi Reference Liu, Zhang and Valocchi2012b ; Liu & Zhang Reference Liu and Zhang2015) and contact line dynamics with contact angle hysteresis (Ba et al. Reference Ba, Liu, Sun and Zheng2013; Liu et al. Reference Liu, Ju, Wang, Xi and Zhang2015). The colour-gradient model has recently been attempted to simulate interfacial flows with insoluble surfactants by Farhat et al. (Reference Farhat, Celiker, Singh and Lee2011). However, their model is not viable because of the following limitations. (1) The model solves a surfactant evolution equation of sharp-interface form (Stone & Leal Reference Stone and Leal1990) over a diffuse interface, and incompatibility would arise as a volume-distribution surfactant concentration should be used instead of its surface counterpart from a diffuse-interface point of view. (2) It solves the surfactant evolution equation in the interfacial region only rather than in the entire fluid domain, and thus initialization techniques for the surfactant concentration at the emerging interfacial nodes need to be developed, which would inevitably increase the modelling complexity and errors. (3) It does not consider the Marangoni stress, which are unphysical and could have important effects on the droplet behaviour. In addition, this model may not be suitable for extension to more complicated systems, such as soluble surfactant solutions.
To model and simulate droplet dynamics with insoluble surfactants, a hybrid method is proposed with a recently improved LB colour-gradient model to describe the immiscible two-phase flow, and a finite difference (FD) method to solve a convection–diffusion equation of diffuse-interface form, originally designed in the context of the phase-field method, for surfactant transport. The interfacial tension force and the Marangoni stress are both modelled using the concept of a continuum surface force. An equation of state that describes how the interfacial tension is influenced by the surfactant concentration will couple the LB and FD simulations dynamically. The capability and accuracy of this hybrid method will be assessed by simulating the deformation of a surfactant-laden droplet in a 3D extensional flow and in a 2D shear flow. It will then be used to investigate the effect of surfactants on the deformation and breakup of a single droplet in a 3D shear flow, where the critical conditions of droplet breakup are explored in a surfactant-laden system with varying confinement ratios and Reynolds numbers for the first time. Finally, we will study the collision of two equal-sized droplets in a shear flow.
2 Numerical method
We develop a hybrid LB–FD method to simulate the interfacial dynamics with insoluble surfactants. This method uses a recently improved LB colour-gradient model (Liu et al. Reference Liu, Zhang and Valocchi2012b ) to simulate immiscible two-phase flows. Compared with the commonly used LB colour-gradient models (Lishchuk, Care & Halliday Reference Lishchuk, Care and Halliday2003; Halliday, Hollis & Care Reference Halliday, Hollis and Care2007; Liu et al. Reference Liu, Valocchi and Kang2012a ; Ba et al. Reference Ba, Liu, Sun and Zheng2013), an additional interfacial Marangoni force that arises from the interfacial tension gradient due to the non-uniform distribution of surfactants is incorporated into the perturbation term. To be compatible with the diffuse nature of the two-phase interface obtained by the colour-gradient model, a convection–diffusion equation of diffuse-interface form to describe the transport of the surfactant concentration is introduced and solved by the FD method. The use of an evolution equation of diffuse-interface form not only allows us to solve the surfactant concentration in the entire fluid domain without additional extension or initialization procedures, but also offers great simplicity in dealing with topological changes such as the interface rupturing and merging. However, it should be noted that the present method is limited to binary fluids with similar densities and to relatively low Reynolds number, which could be improved by using the multiple-relaxation-time model developed in Ba et al. (Reference Ba, Liu, Li, Kang and Sun2016).
2.1 The LB colour-gradient model for immiscible two-phase flows
The model we are using for two-phase flow simulations is a diffuse-interface LB colour-gradient model, where we introduce the interfacial tension force and Marangoni stress as well as the phase segregation in accordance with Liu et al. (Reference Liu, Zhang and Valocchi2012b
). In this model, distribution functions
![]() $f_{i}^{R}$
and
$f_{i}^{R}$
and
![]() $f_{i}^{B}$
are used to represent the red and blue fluids, and the total distribution function is defined as
$f_{i}^{B}$
are used to represent the red and blue fluids, and the total distribution function is defined as
![]() $f_{i}=f_{i}^{R}+f_{i}^{B}$
, where the subscript
$f_{i}=f_{i}^{R}+f_{i}^{B}$
, where the subscript
![]() $i$
is the lattice velocity direction and ranges from 0 to
$i$
is the lattice velocity direction and ranges from 0 to
![]() $(n-1)$
for a given D
$(n-1)$
for a given D
![]() $m$
Q
$m$
Q
![]() $n$
lattice model. In this study, the D2Q9 and D3Q19 lattice models are used for 2D and 3D simulations respectively. Their corresponding lattice velocities
$n$
lattice model. In this study, the D2Q9 and D3Q19 lattice models are used for 2D and 3D simulations respectively. Their corresponding lattice velocities
![]() $\boldsymbol{e}_{i}$
and weighting factors
$\boldsymbol{e}_{i}$
and weighting factors
![]() $w_{i}$
can be found in Mei et al. (Reference Mei, Yu, Shyy and Luo2002).
$w_{i}$
can be found in Mei et al. (Reference Mei, Yu, Shyy and Luo2002).
The present colour-gradient model consists of three steps, i.e. collision step, recolouring step and streaming step. First, the collision step reads as
where
![]() $f_{i}\left(\boldsymbol{x},t\right)$
is the total distribution function in the
$f_{i}\left(\boldsymbol{x},t\right)$
is the total distribution function in the
![]() $i$
th velocity direction at the position
$i$
th velocity direction at the position
![]() $\boldsymbol{x}$
and time
$\boldsymbol{x}$
and time
![]() $t$
,
$t$
,
![]() $f_{i}^{\dagger }$
and
$f_{i}^{\dagger }$
and
![]() $f_{i}^{eq}$
are the post-collision and equilibrium distribution functions respectively,
$f_{i}^{eq}$
are the post-collision and equilibrium distribution functions respectively,
![]() $\unicode[STIX]{x1D714}$
is the dimensionless relaxation parameter related to the fluid viscosity and
$\unicode[STIX]{x1D714}$
is the dimensionless relaxation parameter related to the fluid viscosity and
![]() $\unicode[STIX]{x1D6F7}_{i}$
is the perturbation term.
$\unicode[STIX]{x1D6F7}_{i}$
is the perturbation term.
The equilibrium distribution function is obtained by a second-order Taylor expansion of the Maxwell–Boltzmann distribution with respect to the local fluid velocity
![]() $\boldsymbol{u}$
,
$\boldsymbol{u}$
,
where
![]() $\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}^{R}+\unicode[STIX]{x1D70C}^{B}$
is the total density, with the superscripts ‘
$\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}^{R}+\unicode[STIX]{x1D70C}^{B}$
is the total density, with the superscripts ‘
![]() $R$
’ and ‘
$R$
’ and ‘
![]() $B$
’ referring to the red and blue fluids respectively, and
$B$
’ referring to the red and blue fluids respectively, and
![]() $c_{s}=1/\sqrt{3}$
is the speed of sound.
$c_{s}=1/\sqrt{3}$
is the speed of sound.
The perturbation term contributes to the mixed interfacial regions and generates an interfacial force
![]() $\boldsymbol{F}_{s}$
. The perturbation term is given by (Guo, Zheng & Shi Reference Guo, Zheng and Shi2002a
; Liu et al.
Reference Liu, Zhang and Valocchi2012b
)
$\boldsymbol{F}_{s}$
. The perturbation term is given by (Guo, Zheng & Shi Reference Guo, Zheng and Shi2002a
; Liu et al.
Reference Liu, Zhang and Valocchi2012b
)
where
![]() $\unicode[STIX]{x1D6FF}_{t}$
is the time step and the local fluid velocity is defined by
$\unicode[STIX]{x1D6FF}_{t}$
is the time step and the local fluid velocity is defined by
![]() $\unicode[STIX]{x1D70C}\boldsymbol{u}(\boldsymbol{x},t)=\sum _{i}f_{i}(\boldsymbol{x},t)\boldsymbol{e}_{i}+\boldsymbol{F}_{s}(\boldsymbol{x},t)\unicode[STIX]{x1D6FF}_{t}/2$
. Following Liu et al. (Reference Liu, Zhang and Valocchi2012b
), the concept of continuum surface force (CSF) is used to model the interfacial force with dynamic interfacial tension and Marangoni stress, which reads as
$\unicode[STIX]{x1D70C}\boldsymbol{u}(\boldsymbol{x},t)=\sum _{i}f_{i}(\boldsymbol{x},t)\boldsymbol{e}_{i}+\boldsymbol{F}_{s}(\boldsymbol{x},t)\unicode[STIX]{x1D6FF}_{t}/2$
. Following Liu et al. (Reference Liu, Zhang and Valocchi2012b
), the concept of continuum surface force (CSF) is used to model the interfacial force with dynamic interfacial tension and Marangoni stress, which reads as
where
![]() $\unicode[STIX]{x1D70C}^{N}=(\unicode[STIX]{x1D70C}^{R}-\unicode[STIX]{x1D70C}^{B})/\unicode[STIX]{x1D70C}$
is a colour indicator and is introduced to identify the location of the interface,
$\unicode[STIX]{x1D70C}^{N}=(\unicode[STIX]{x1D70C}^{R}-\unicode[STIX]{x1D70C}^{B})/\unicode[STIX]{x1D70C}$
is a colour indicator and is introduced to identify the location of the interface,
![]() $\unicode[STIX]{x1D70E}$
is the interfacial tension,
$\unicode[STIX]{x1D70E}$
is the interfacial tension,
![]() $\unicode[STIX]{x1D735}_{s}=(\unicode[STIX]{x1D644}-\boldsymbol{n}\otimes \boldsymbol{n})\boldsymbol{\cdot }\unicode[STIX]{x1D735}$
is the surface gradient operator,
$\unicode[STIX]{x1D735}_{s}=(\unicode[STIX]{x1D644}-\boldsymbol{n}\otimes \boldsymbol{n})\boldsymbol{\cdot }\unicode[STIX]{x1D735}$
is the surface gradient operator,
![]() $\unicode[STIX]{x1D644}$
is the second-order identity tensor,
$\unicode[STIX]{x1D644}$
is the second-order identity tensor,
![]() $\boldsymbol{n}$
is the interfacial unit normal vector, defined by
$\boldsymbol{n}$
is the interfacial unit normal vector, defined by
![]() $\boldsymbol{n}=-\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}^{N}/|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}^{N}|$
and
$\boldsymbol{n}=-\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}^{N}/|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}^{N}|$
and
![]() $\unicode[STIX]{x1D705}$
is the local interface curvature, related to
$\unicode[STIX]{x1D705}$
is the local interface curvature, related to
![]() $\boldsymbol{n}$
by
$\boldsymbol{n}$
by
It should be noted that the first term on the right-hand side of (2.4) is the interfacial tension force (the normal force) and the second term is the Marangoni stress (the tangential force) that results from the non-uniform distribution of surfactants along the interface. It is worth emphasizing that neglect of the Marangoni stress term could lead to significant errors in simulation of interfacial flows with variable interfacial tension (Sui Reference Sui2014).
In the presence of surfactants, an equation of state (EOS) is required to relate the interfacial tension to the surfactant concentration. Often, a Langmuir EOS in the form
is used, where
![]() $\unicode[STIX]{x1D713}$
is the surfactant concentration,
$\unicode[STIX]{x1D713}$
is the surfactant concentration,
![]() $\unicode[STIX]{x1D713}_{\infty }$
is the surfactant concentration at the maximum packing,
$\unicode[STIX]{x1D713}_{\infty }$
is the surfactant concentration at the maximum packing,
![]() $\unicode[STIX]{x1D70E}_{0}$
is the interfacial tension of a clean interface (i.e.
$\unicode[STIX]{x1D70E}_{0}$
is the interfacial tension of a clean interface (i.e.
![]() $\unicode[STIX]{x1D713}=0$
),
$\unicode[STIX]{x1D713}=0$
),
![]() $E_{0}=RT\unicode[STIX]{x1D713}_{\infty }/\unicode[STIX]{x1D70E}_{0}$
is the elasticity number that measures the sensitivity of
$E_{0}=RT\unicode[STIX]{x1D713}_{\infty }/\unicode[STIX]{x1D70E}_{0}$
is the elasticity number that measures the sensitivity of
![]() $\unicode[STIX]{x1D70E}$
to the variation of
$\unicode[STIX]{x1D70E}$
to the variation of
![]() $\unicode[STIX]{x1D713}$
,
$\unicode[STIX]{x1D713}$
,
![]() $R$
is the constant of ideal gas and
$R$
is the constant of ideal gas and
![]() $T$
is the absolute temperature. For low surfactant concentration, the following linear approximation of the Langmuir equation can be used:
$T$
is the absolute temperature. For low surfactant concentration, the following linear approximation of the Langmuir equation can be used:
As in Xu et al. (Reference Xu, Li, Lowengrub and Zhao2006), we quantify the initial average surfactant concentration
![]() $\unicode[STIX]{x1D713}_{0}$
through the surfactant coverage, which is defined as
$\unicode[STIX]{x1D713}_{0}$
through the surfactant coverage, which is defined as
![]() $x_{in}=\unicode[STIX]{x1D713}_{0}/\unicode[STIX]{x1D713}_{\infty }$
.
$x_{in}=\unicode[STIX]{x1D713}_{0}/\unicode[STIX]{x1D713}_{\infty }$
.
Using the Chapman–Enskog expansion, it can be proved that (2.1)–(2.3) exactly recover the Navier–Stokes equations for two-phase flow (Liu et al.
Reference Liu, Zhang and Valocchi2012b
), where the pressure and the dynamic viscosity of the fluid mixture are defined by
![]() $p=\unicode[STIX]{x1D70C}c_{s}^{2}$
and
$p=\unicode[STIX]{x1D70C}c_{s}^{2}$
and
![]() $\unicode[STIX]{x1D707}=\left(1/\unicode[STIX]{x1D714}-1/2\right)\unicode[STIX]{x1D70C}c_{s}^{2}\unicode[STIX]{x1D6FF}_{t}$
. To allow for unequal viscosities of the two fluids, we determine
$\unicode[STIX]{x1D707}=\left(1/\unicode[STIX]{x1D714}-1/2\right)\unicode[STIX]{x1D70C}c_{s}^{2}\unicode[STIX]{x1D6FF}_{t}$
. To allow for unequal viscosities of the two fluids, we determine
![]() $\unicode[STIX]{x1D707}$
by a harmonic mean (Liu et al.
Reference Liu, Valocci, Werth, Kang and Oostrom2014),
$\unicode[STIX]{x1D707}$
by a harmonic mean (Liu et al.
Reference Liu, Valocci, Werth, Kang and Oostrom2014),
where
![]() $\unicode[STIX]{x1D707}^{k}$
(
$\unicode[STIX]{x1D707}^{k}$
(
![]() $k=R$
or
$k=R$
or
![]() $B$
) is the dynamic viscosity of fluid
$B$
) is the dynamic viscosity of fluid
![]() $k$
.
$k$
.
Then, the recolouring (segregation) algorithm of Latva-Kokko & Rothman (Reference Latva-Kokko and Rothman2005) is used to promote phase segregation and ensure the immiscibility of both fluids. Following Latva-Kokko & Rothman (Reference Latva-Kokko and Rothman2005), the recoloured distribution functions of the red and blue fluids are
 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle f_{i}^{R\ddagger }(\boldsymbol{x},t)=\frac{\unicode[STIX]{x1D70C}^{R}}{\unicode[STIX]{x1D70C}}f_{i}^{\dagger }(\boldsymbol{x},t)+\unicode[STIX]{x1D6FD}w_{i}\frac{\unicode[STIX]{x1D70C}^{R}\unicode[STIX]{x1D70C}^{B}}{\unicode[STIX]{x1D70C}}\boldsymbol{e}_{i}\boldsymbol{\cdot }\boldsymbol{n},\\ \displaystyle f_{i}^{B\ddagger }(\boldsymbol{x},t)=\frac{\unicode[STIX]{x1D70C}^{B}}{\unicode[STIX]{x1D70C}}f_{i}^{\dagger }(\boldsymbol{x},t)-\unicode[STIX]{x1D6FD}w_{i}\frac{\unicode[STIX]{x1D70C}^{R}\unicode[STIX]{x1D70C}^{B}}{\unicode[STIX]{x1D70C}}\boldsymbol{e}_{i}\boldsymbol{\cdot }\boldsymbol{n},\end{array}\right\} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle f_{i}^{R\ddagger }(\boldsymbol{x},t)=\frac{\unicode[STIX]{x1D70C}^{R}}{\unicode[STIX]{x1D70C}}f_{i}^{\dagger }(\boldsymbol{x},t)+\unicode[STIX]{x1D6FD}w_{i}\frac{\unicode[STIX]{x1D70C}^{R}\unicode[STIX]{x1D70C}^{B}}{\unicode[STIX]{x1D70C}}\boldsymbol{e}_{i}\boldsymbol{\cdot }\boldsymbol{n},\\ \displaystyle f_{i}^{B\ddagger }(\boldsymbol{x},t)=\frac{\unicode[STIX]{x1D70C}^{B}}{\unicode[STIX]{x1D70C}}f_{i}^{\dagger }(\boldsymbol{x},t)-\unicode[STIX]{x1D6FD}w_{i}\frac{\unicode[STIX]{x1D70C}^{R}\unicode[STIX]{x1D70C}^{B}}{\unicode[STIX]{x1D70C}}\boldsymbol{e}_{i}\boldsymbol{\cdot }\boldsymbol{n},\end{array}\right\} & & \displaystyle\end{eqnarray}$$
where
![]() $f_{i}^{R\ddagger }$
and
$f_{i}^{R\ddagger }$
and
![]() $f_{i}^{B\ddagger }$
are the recoloured distribution functions of the red and blue fluids respectively. Here,
$f_{i}^{B\ddagger }$
are the recoloured distribution functions of the red and blue fluids respectively. Here,
![]() $\unicode[STIX]{x1D6FD}$
is the segregation parameter and is set to be 0.7 to maintain a narrow interface thickness (around 4–5 lattices) and keep spurious velocities low (Halliday et al.
Reference Halliday, Hollis and Care2007; Gupta & Kumar Reference Gupta and Kumar2010). Moreover, Liu et al. (Reference Liu, Valocchi and Kang2012a
) indicated that this choice is necessary to reproduce the correct dynamical behaviour of droplets.
$\unicode[STIX]{x1D6FD}$
is the segregation parameter and is set to be 0.7 to maintain a narrow interface thickness (around 4–5 lattices) and keep spurious velocities low (Halliday et al.
Reference Halliday, Hollis and Care2007; Gupta & Kumar Reference Gupta and Kumar2010). Moreover, Liu et al. (Reference Liu, Valocchi and Kang2012a
) indicated that this choice is necessary to reproduce the correct dynamical behaviour of droplets.
After the recolouring step, the red and blue distribution functions propagate to the neighbouring lattice nodes, known as the propagation or streaming step,
with the post-propagation distribution functions used to compute the densities of both fluids by
![]() $\unicode[STIX]{x1D70C}^{k}=\sum _{i}f_{i}^{k}$
.
$\unicode[STIX]{x1D70C}^{k}=\sum _{i}f_{i}^{k}$
.
2.2 Finite difference method for surfactant transport
With a sharp-interface representation, the transport of surfactant concentration is governed by a convection–diffusion equation with a source-like term to account for interfacial stretching and distortion (Stone & Leal Reference Stone and Leal1990),
where
![]() $\boldsymbol{u}_{s}=(\boldsymbol{I}-\boldsymbol{n}\otimes \boldsymbol{n})\boldsymbol{\cdot }\boldsymbol{u}$
is the tangential velocity and
$\boldsymbol{u}_{s}=(\boldsymbol{I}-\boldsymbol{n}\otimes \boldsymbol{n})\boldsymbol{\cdot }\boldsymbol{u}$
is the tangential velocity and
![]() $D_{s}$
is the surfactant diffusivity. This equation has been commonly used to describe the surfactant concentration evolution in interface-tracking methods (Zhang et al.
Reference Zhang, Eckmann and Ayyaswamy2006; Feigl et al.
Reference Feigl, Megias-Alguacil, Fischer and Windhab2007; Jin & Stebe Reference Jin and Stebe2007; Lai et al.
Reference Lai, Tseng and Huang2008; Muradoglu & Tryggvason Reference Muradoglu and Tryggvason2008) and is solved along a sharp interface represented by Lagrangian markers or particles. Assuming that the surfactant concentration
$D_{s}$
is the surfactant diffusivity. This equation has been commonly used to describe the surfactant concentration evolution in interface-tracking methods (Zhang et al.
Reference Zhang, Eckmann and Ayyaswamy2006; Feigl et al.
Reference Feigl, Megias-Alguacil, Fischer and Windhab2007; Jin & Stebe Reference Jin and Stebe2007; Lai et al.
Reference Lai, Tseng and Huang2008; Muradoglu & Tryggvason Reference Muradoglu and Tryggvason2008) and is solved along a sharp interface represented by Lagrangian markers or particles. Assuming that the surfactant concentration
![]() $\unicode[STIX]{x1D713}$
could be extended off the interface
$\unicode[STIX]{x1D713}$
could be extended off the interface
![]() $\unicode[STIX]{x1D6E4}$
, an equivalent Eulerian formulation was derived from (2.11) by Xu & Zhao (Reference Xu and Zhao2003),
$\unicode[STIX]{x1D6E4}$
, an equivalent Eulerian formulation was derived from (2.11) by Xu & Zhao (Reference Xu and Zhao2003),
It should be noted that an additional Hamilton–Jacobian equation, similar to the one used for re-initialization in the level-set method, needs to be solved in order to extend the surfactant concentration on the interface to its neighbourhood (Xu & Zhao Reference Xu and Zhao2003; Xu et al. Reference Xu, Li, Lowengrub and Zhao2006, Reference Xu, Yang and Lowengrub2012). This extension enables one to solve the surfactant transport equation, i.e. (2.12), in an Eulerian framework by using FD or finite element methods.
By extending (2.12) to the general fluid domain
![]() $\unicode[STIX]{x1D6FA}$
with the aid of an auxiliary Dirac function, Teigen et al. (Reference Teigen, Song, Lowengrub and Voigt2011) recently proposed a surfactant evolution equation of diffuse-interface form,
$\unicode[STIX]{x1D6FA}$
with the aid of an auxiliary Dirac function, Teigen et al. (Reference Teigen, Song, Lowengrub and Voigt2011) recently proposed a surfactant evolution equation of diffuse-interface form,
where the Dirac function
![]() $\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6E4}}$
is used to localize the surfactant concentration explicitly at the interface and should satisfy
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6E4}}$
is used to localize the surfactant concentration explicitly at the interface and should satisfy
![]() $\int _{\unicode[STIX]{x1D6E4}}\unicode[STIX]{x1D713}\,\text{d}\unicode[STIX]{x1D6E4}=\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D713}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6E4}}\,\text{d}\unicode[STIX]{x1D6FA}$
(Teigen et al.
Reference Teigen, Song, Lowengrub and Voigt2011).
$\int _{\unicode[STIX]{x1D6E4}}\unicode[STIX]{x1D713}\,\text{d}\unicode[STIX]{x1D6E4}=\int _{\unicode[STIX]{x1D6FA}}\unicode[STIX]{x1D713}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6E4}}\,\text{d}\unicode[STIX]{x1D6FA}$
(Teigen et al.
Reference Teigen, Song, Lowengrub and Voigt2011).
The surfactant evolution equation of diffuse-interface form has been combined with the phase-field method to simulate interfacial flows with surfactants. In spite of its great success and ongoing advances, the phase-field method is still criticized as it cannot conserve mass for each fluid, the choice of an optimal mobility remains an open question and small droplets or bubbles are prone to dissolving unphysically. By contrast, the LB colour-gradient model possesses many advantages in simulating multiphase and multicomponent flows, including strict mass conservation for each fluid, high numerical accuracy and good numerical stability for a broad range of viscosity ratios. In addition, the colour-gradient model is perfectly compatible with the surfactant evolution equation of diffuse-interface form because its interface is of diffuse nature and it adopts a Dirac function to model the interfacial force (Liu et al.
Reference Liu, Zhang and Valocchi2012b
). To be consistent with the colour-gradient model, the Dirac function in (2.13) is taken as
![]() $\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6E4}}=|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}^{N}|/2$
. Thus, the surfactant evolution equation of diffuse-interface form can be further written as
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6E4}}=|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}^{N}|/2$
. Thus, the surfactant evolution equation of diffuse-interface form can be further written as
It should be noted that (2.14), in combination with the colour-gradient model, is well suited to handling the interface breakup and coalescence without invoking any ad hoc criteria, and it does not need to solve an additional equation to extend the surfactant concentration off the interface, greatly simplifying the computation. More importantly, (2.14) can be easily extended to modelling of soluble surfactants (Teigen et al. Reference Teigen, Song, Lowengrub and Voigt2011).
In the present work, (2.14) is adopted to describe the surfactant transport, and it is solved by the FD method using a modified Crank–Nicholson scheme for the time discretization (Xu & Zhao Reference Xu and Zhao2003),
 $$\begin{eqnarray}\displaystyle & \displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \frac{\unicode[STIX]{x1D713}^{t+\unicode[STIX]{x1D6FF}_{t}}|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}^{N}|^{t+\unicode[STIX]{x1D6FF}_{t}}-\unicode[STIX]{x1D713}^{t}|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}^{N}|^{t}}{\unicode[STIX]{x1D6FF}_{t}}=D_{s}|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}^{N}|\frac{\unicode[STIX]{x1D6FB}^{2}\unicode[STIX]{x1D713}^{t+\unicode[STIX]{x1D6FF}_{t}}+\unicode[STIX]{x1D6FB}^{2}\unicode[STIX]{x1D713}^{t}}{2}+{\mathcal{S}}^{t},~~\text{for}~t=0,\\ \displaystyle \frac{\unicode[STIX]{x1D713}^{t+\unicode[STIX]{x1D6FF}_{t}}|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}^{N}|^{t+\unicode[STIX]{x1D6FF}_{t}}-\unicode[STIX]{x1D713}^{t}|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}^{N}|^{t}}{\unicode[STIX]{x0394}t}=D_{s}|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}^{N}|\frac{\unicode[STIX]{x1D6FB}^{2}\unicode[STIX]{x1D713}^{t+\unicode[STIX]{x1D6FF}_{t}}+\unicode[STIX]{x1D6FB}^{2}\unicode[STIX]{x1D713}^{t}}{2}+\frac{3}{2}{\mathcal{S}}^{t}-\frac{1}{2}{\mathcal{S}}^{t-1},~~\text{for}~t>1,\end{array}\right\} & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \frac{\unicode[STIX]{x1D713}^{t+\unicode[STIX]{x1D6FF}_{t}}|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}^{N}|^{t+\unicode[STIX]{x1D6FF}_{t}}-\unicode[STIX]{x1D713}^{t}|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}^{N}|^{t}}{\unicode[STIX]{x1D6FF}_{t}}=D_{s}|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}^{N}|\frac{\unicode[STIX]{x1D6FB}^{2}\unicode[STIX]{x1D713}^{t+\unicode[STIX]{x1D6FF}_{t}}+\unicode[STIX]{x1D6FB}^{2}\unicode[STIX]{x1D713}^{t}}{2}+{\mathcal{S}}^{t},~~\text{for}~t=0,\\ \displaystyle \frac{\unicode[STIX]{x1D713}^{t+\unicode[STIX]{x1D6FF}_{t}}|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}^{N}|^{t+\unicode[STIX]{x1D6FF}_{t}}-\unicode[STIX]{x1D713}^{t}|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}^{N}|^{t}}{\unicode[STIX]{x0394}t}=D_{s}|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}^{N}|\frac{\unicode[STIX]{x1D6FB}^{2}\unicode[STIX]{x1D713}^{t+\unicode[STIX]{x1D6FF}_{t}}+\unicode[STIX]{x1D6FB}^{2}\unicode[STIX]{x1D713}^{t}}{2}+\frac{3}{2}{\mathcal{S}}^{t}-\frac{1}{2}{\mathcal{S}}^{t-1},~~\text{for}~t>1,\end{array}\right\} & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
with
![]() ${\mathcal{S}}=-\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D735}(\unicode[STIX]{x1D713}|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}^{N}|)+D_{s}(\unicode[STIX]{x1D735}|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}^{N}|)\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}$
. In (2.15), all of the spatial derivatives are discretized using standard central difference schemes except for the convection term
${\mathcal{S}}=-\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D735}(\unicode[STIX]{x1D713}|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}^{N}|)+D_{s}(\unicode[STIX]{x1D735}|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}^{N}|)\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}$
. In (2.15), all of the spatial derivatives are discretized using standard central difference schemes except for the convection term
![]() $\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D735}(\unicode[STIX]{x1D713}|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}^{N}|)$
, which is discretized using a third-order weighted essentially non-oscillatory (WENO) scheme (Jiang & Shu Reference Jiang and Shu1996; Xu & Zhao Reference Xu and Zhao2003). The WENO scheme has the advantages that it can handle steep gradients well and fewer grid points are needed to achieve a high-order resolution.
$\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D735}(\unicode[STIX]{x1D713}|\unicode[STIX]{x1D735}\unicode[STIX]{x1D70C}^{N}|)$
, which is discretized using a third-order weighted essentially non-oscillatory (WENO) scheme (Jiang & Shu Reference Jiang and Shu1996; Xu & Zhao Reference Xu and Zhao2003). The WENO scheme has the advantages that it can handle steep gradients well and fewer grid points are needed to achieve a high-order resolution.
The resulting linear system for
![]() $\unicode[STIX]{x1D713}^{t+\unicode[STIX]{x1D6FF}_{t}}$
from (2.15) is symmetric positive definite, similar to that from a transient heat conduction equation. It can be solved by various efficient and robust algorithms, e.g. the successive over relaxation (SOR) method or the conjugate gradient method (Saad Reference Saad2003). In our numerical computations, we simply use the SOR method with the relaxation factor fixed at 1.2.
$\unicode[STIX]{x1D713}^{t+\unicode[STIX]{x1D6FF}_{t}}$
from (2.15) is symmetric positive definite, similar to that from a transient heat conduction equation. It can be solved by various efficient and robust algorithms, e.g. the successive over relaxation (SOR) method or the conjugate gradient method (Saad Reference Saad2003). In our numerical computations, we simply use the SOR method with the relaxation factor fixed at 1.2.
3 Numerical validation
The hybrid LB–FD method is validated against the available literature data for a surfactant-laden droplet subject to a 3D extensional flow and a 2D shear flow.
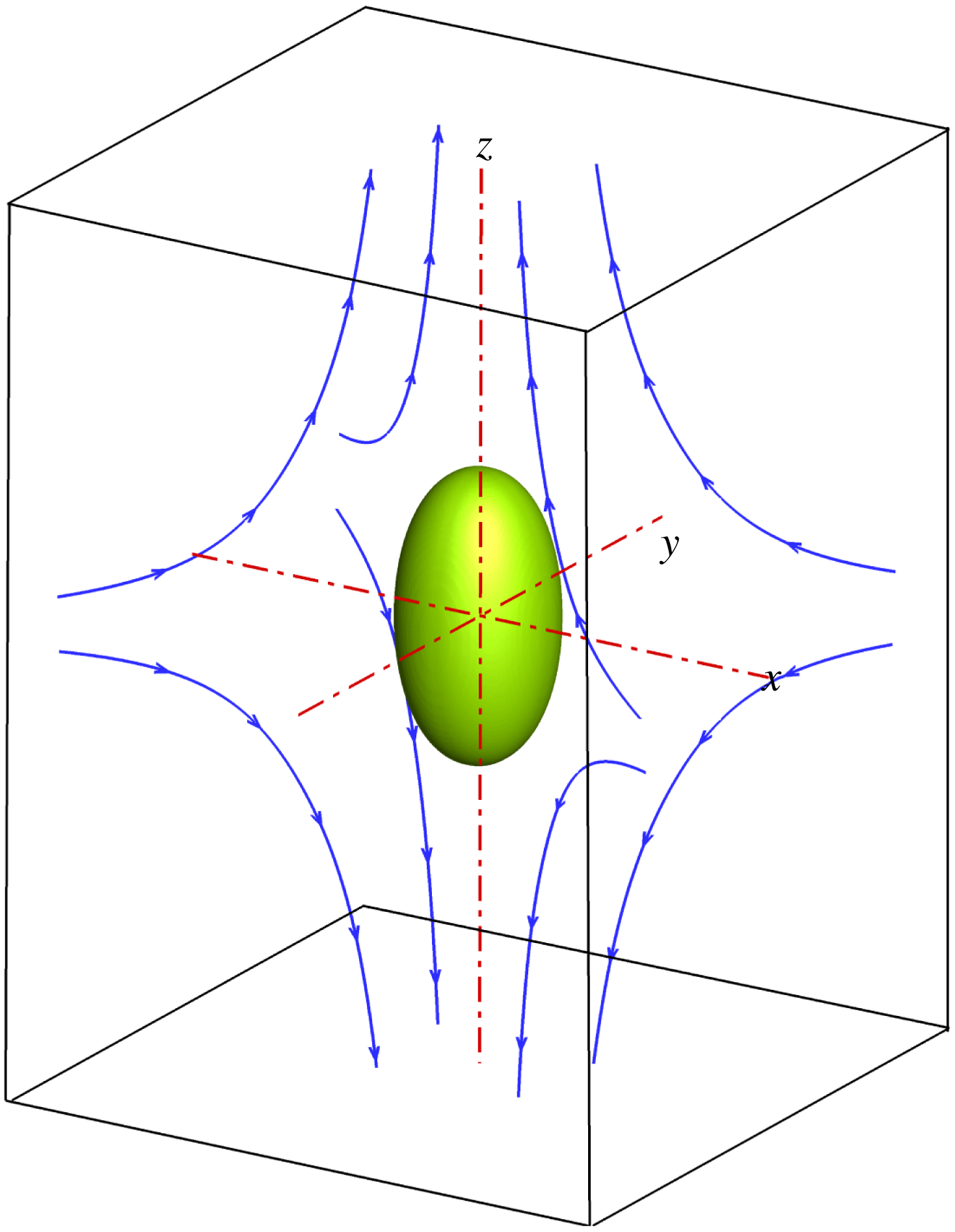
Figure 1. Illustration of a droplet in a 3D extensional flow.
3.1 Droplet deformation in an extensional flow
We first simulate the deformation of a surfactant-covered droplet in a 3D extensional flow, and compare the numerical results with those obtained from the BIM (Stone & Leal Reference Stone and Leal1990; Feigl et al.
Reference Feigl, Megias-Alguacil, Fischer and Windhab2007). As sketched in figure 1, a spherical droplet (red fluid) of radius
![]() $R$
is initially suspended in an immiscible liquid (blue fluid) in an external extensional flow, where the far-field flow velocity is given by
$R$
is initially suspended in an immiscible liquid (blue fluid) in an external extensional flow, where the far-field flow velocity is given by
 $$\begin{eqnarray}\boldsymbol{u}_{\infty }(\boldsymbol{x})=\dot{\unicode[STIX]{x1D6FE}}\left(\begin{array}{@{}ccc@{}}-0.5 & 0 & 0\\ 0 & -0.5 & 0\\ 0 & 0 & 1\end{array}\right)\boldsymbol{\cdot }\boldsymbol{x}.\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{u}_{\infty }(\boldsymbol{x})=\dot{\unicode[STIX]{x1D6FE}}\left(\begin{array}{@{}ccc@{}}-0.5 & 0 & 0\\ 0 & -0.5 & 0\\ 0 & 0 & 1\end{array}\right)\boldsymbol{\cdot }\boldsymbol{x}.\end{eqnarray}$$
Here,
![]() $\dot{\unicode[STIX]{x1D6FE}}$
is the shear rate and
$\dot{\unicode[STIX]{x1D6FE}}$
is the shear rate and
![]() $\boldsymbol{x}$
is the position vector. In the presence of surfactants, the droplet behaviour can be characterized by several important dimensionless numbers, including the Reynolds number (
$\boldsymbol{x}$
is the position vector. In the presence of surfactants, the droplet behaviour can be characterized by several important dimensionless numbers, including the Reynolds number (
![]() $Re$
), the capillary number (
$Re$
), the capillary number (
![]() $Ca$
) and the surface Péclet number (
$Ca$
) and the surface Péclet number (
![]() $Pe$
), which are defined as follows:
$Pe$
), which are defined as follows:
In addition, for a diffuse-interface model, the Cahn number should be small enough to approach the sharp-interface limit, and it is defined by
![]() $Cn=\unicode[STIX]{x1D709}/R$
, where
$Cn=\unicode[STIX]{x1D709}/R$
, where
![]() $\unicode[STIX]{x1D709}=1/(6k\unicode[STIX]{x1D6FD})$
is a measure of the diffuse-interface thickness, with
$\unicode[STIX]{x1D709}=1/(6k\unicode[STIX]{x1D6FD})$
is a measure of the diffuse-interface thickness, with
![]() $k=0.1504$
for the D2Q9 model and
$k=0.1504$
for the D2Q9 model and
![]() $k=0.134$
for the D3Q19 model (Riaud et al.
Reference Riaud, Zhao, Wang, Cheng and Luo2014).
$k=0.134$
for the D3Q19 model (Riaud et al.
Reference Riaud, Zhao, Wang, Cheng and Luo2014).
For creeping flows, i.e.
![]() $Re\ll 1$
and
$Re\ll 1$
and
![]() $Ca\ll 1$
, the droplet will eventually deform into an ellipsoidal shape, which is usually characterized by the deformation parameter
$Ca\ll 1$
, the droplet will eventually deform into an ellipsoidal shape, which is usually characterized by the deformation parameter
![]() $D_{f}$
and the dimensionless extensional length
$D_{f}$
and the dimensionless extensional length
![]() $L$
,
$L$
,
where
![]() $a$
and
$a$
and
![]() $b$
are the half-lengths of the major and minor axes of the droplet respectively.
$b$
are the half-lengths of the major and minor axes of the droplet respectively.
The simulations are first run at
![]() $Re=0.05$
for a spherical droplet of
$Re=0.05$
for a spherical droplet of
![]() $R=30$
lattices (the corresponding Cahn number is
$R=30$
lattices (the corresponding Cahn number is
![]() $Cn=1/(6k\unicode[STIX]{x1D6FD}R)=0.0592$
), with the effective capillary number (
$Cn=1/(6k\unicode[STIX]{x1D6FD}R)=0.0592$
), with the effective capillary number (
![]() $Ca_{e}$
) varying from 0.028 to 0.11. The effective capillary number is defined as
$Ca_{e}$
) varying from 0.028 to 0.11. The effective capillary number is defined as
and it is used here to keep consistency with Stone & Leal (Reference Stone and Leal1990). The linear EOS (2.6) is used with the elasticity number
![]() $E_{0}=0.1$
. Both fluids are assumed to have equal densities and viscosities, and the surface Péclet number is set as
$E_{0}=0.1$
. Both fluids are assumed to have equal densities and viscosities, and the surface Péclet number is set as
![]() $Pe=10Ca$
. Due to symmetry, we only simulate one octant of the droplet, with a domain size of
$Pe=10Ca$
. Due to symmetry, we only simulate one octant of the droplet, with a domain size of
![]() $100\times 100\times 160$
lattices. To obtain an extensional flow, we apply the non-equilibrium extrapolation boundary condition proposed by Guo, Zheng & Shi (Reference Guo, Zheng and Shi2002b
) at the far field. For all values of
$100\times 100\times 160$
lattices. To obtain an extensional flow, we apply the non-equilibrium extrapolation boundary condition proposed by Guo, Zheng & Shi (Reference Guo, Zheng and Shi2002b
) at the far field. For all values of
![]() $Ca_{e}$
considered, the droplet is continuously elongated along the
$Ca_{e}$
considered, the droplet is continuously elongated along the
![]() $z$
-direction until a steady shape is achieved.
$z$
-direction until a steady shape is achieved.
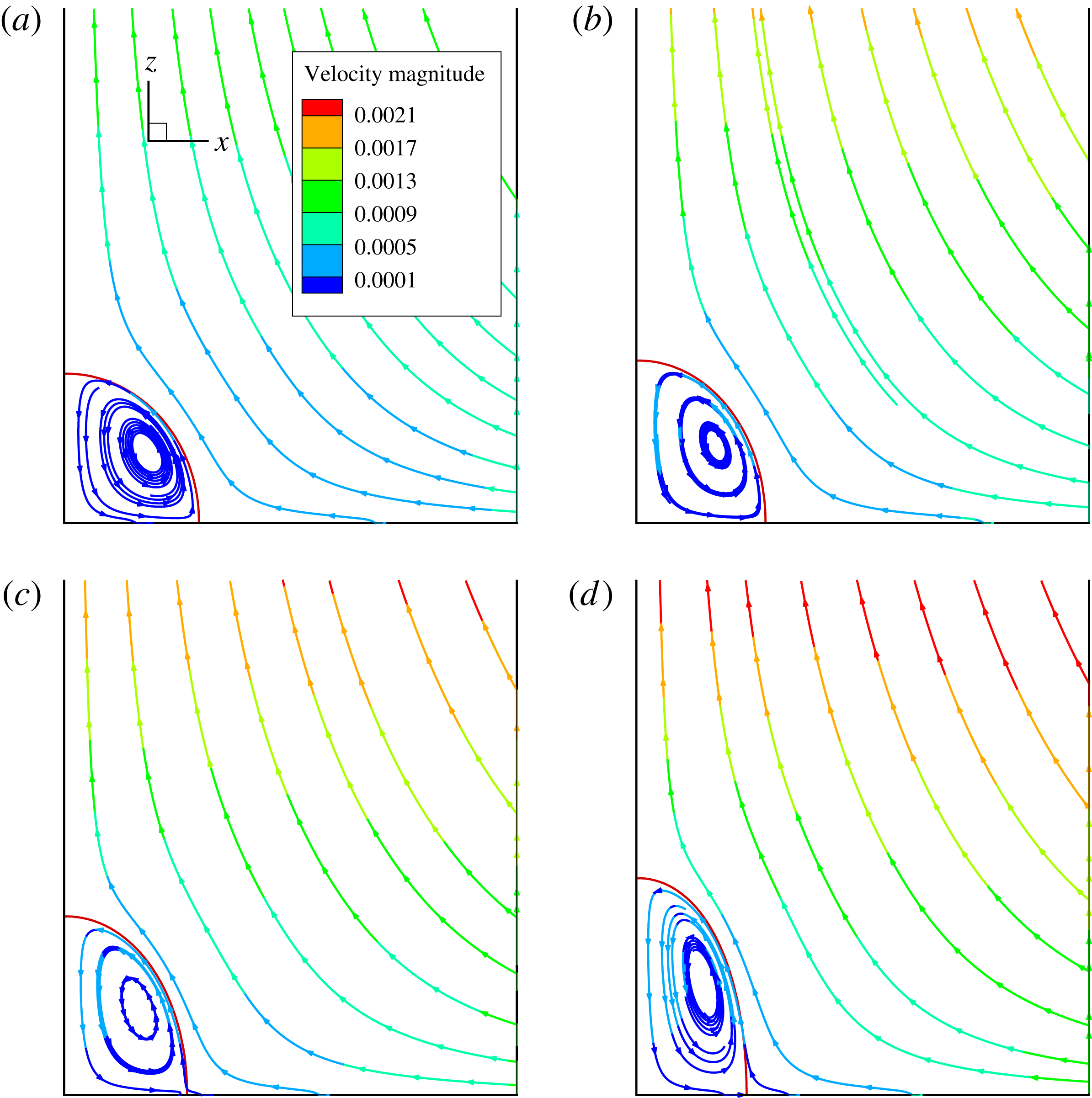
Figure 2. The steady droplet shapes (represented in red) and streamlines at the
![]() $x=0$
plane for effective capillary numbers of (a)
$x=0$
plane for effective capillary numbers of (a)
![]() $Ca_{e}=0.028$
, (b)
$Ca_{e}=0.028$
, (b)
![]() $Ca_{e}=0.057$
, (c)
$Ca_{e}=0.057$
, (c)
![]() $Ca_{e}=0.083$
and (d)
$Ca_{e}=0.083$
and (d)
![]() $Ca_{e}=0.11$
.
$Ca_{e}=0.11$
.
Figure 2 shows the steady droplet shapes and streamlines at the
![]() $x=0$
plane for various values of
$x=0$
plane for various values of
![]() $Ca_{e}$
. It is seen that a single vortex is formed and fully filled inside the droplet in steady state. Moreover, the droplet deformation increases with increasing
$Ca_{e}$
. It is seen that a single vortex is formed and fully filled inside the droplet in steady state. Moreover, the droplet deformation increases with increasing
![]() $Ca_{e}$
. Figure 3 plots the dimensionless surfactant concentration
$Ca_{e}$
. Figure 3 plots the dimensionless surfactant concentration
![]() $\unicode[STIX]{x1D713}^{\ast }=\unicode[STIX]{x1D713}/\unicode[STIX]{x1D713}_{0}$
on the steady droplet interface (represented by
$\unicode[STIX]{x1D713}^{\ast }=\unicode[STIX]{x1D713}/\unicode[STIX]{x1D713}_{0}$
on the steady droplet interface (represented by
![]() $\unicode[STIX]{x1D70C}^{N}=0$
) as a function of
$\unicode[STIX]{x1D70C}^{N}=0$
) as a function of
![]() $z/R$
for different values of
$z/R$
for different values of
![]() $Ca_{e}$
. It is observed that for each
$Ca_{e}$
. It is observed that for each
![]() $Ca_{e}$
, the surfactant concentration reaches its highest value at the tip of the droplet and gradually decreases along the negative direction of the
$Ca_{e}$
, the surfactant concentration reaches its highest value at the tip of the droplet and gradually decreases along the negative direction of the
![]() $z$
-axis.
$z$
-axis.

Figure 3. The dimensionless surfactant concentration
![]() $\unicode[STIX]{x1D713}^{\ast }$
on the steady droplet interface (
$\unicode[STIX]{x1D713}^{\ast }$
on the steady droplet interface (
![]() $\unicode[STIX]{x1D70C}^{N}=0$
) as a function of
$\unicode[STIX]{x1D70C}^{N}=0$
) as a function of
![]() $z/R$
for various values of
$z/R$
for various values of
![]() $Ca_{e}$
.
$Ca_{e}$
.
In addition, we quantify the deformation parameter
![]() $D_{f}$
in steady state, dimensionless extensional length
$D_{f}$
in steady state, dimensionless extensional length
![]() $L$
, and the maximum (
$L$
, and the maximum (
![]() $\unicode[STIX]{x1D713}_{max}^{\ast }$
) and minimum (
$\unicode[STIX]{x1D713}_{max}^{\ast }$
) and minimum (
![]() $\unicode[STIX]{x1D713}_{min}^{\ast }$
) values of the dimensionless surfactant concentration at
$\unicode[STIX]{x1D713}_{min}^{\ast }$
) values of the dimensionless surfactant concentration at
![]() $\unicode[STIX]{x1D70C}^{N}=0$
for various values of
$\unicode[STIX]{x1D70C}^{N}=0$
for various values of
![]() $Ca_{e}$
, which are plotted in figure 4. It is seen that our numerical results for
$Ca_{e}$
, which are plotted in figure 4. It is seen that our numerical results for
![]() $D_{f}$
,
$D_{f}$
,
![]() $L$
,
$L$
,
![]() $\unicode[STIX]{x1D713}_{max}^{\ast }$
and
$\unicode[STIX]{x1D713}_{max}^{\ast }$
and
![]() $\unicode[STIX]{x1D713}_{min}^{\ast }$
are all in good agreement with those obtained by Stone & Leal (Reference Stone and Leal1990) and Feigl et al. (Reference Feigl, Megias-Alguacil, Fischer and Windhab2007). This suggests that the present method can produce equally accurate results to the sharp-interface approach for a finite interface thickness.
$\unicode[STIX]{x1D713}_{min}^{\ast }$
are all in good agreement with those obtained by Stone & Leal (Reference Stone and Leal1990) and Feigl et al. (Reference Feigl, Megias-Alguacil, Fischer and Windhab2007). This suggests that the present method can produce equally accurate results to the sharp-interface approach for a finite interface thickness.

Figure 4. Comparison of the simulated (a) deformation parameter
![]() $D_{f}$
and dimensionless extensional length
$D_{f}$
and dimensionless extensional length
![]() $L$
, and (b) maximum (
$L$
, and (b) maximum (
![]() $\unicode[STIX]{x1D713}_{max}^{\ast }$
) and minimum (
$\unicode[STIX]{x1D713}_{max}^{\ast }$
) and minimum (
![]() $\unicode[STIX]{x1D713}_{min}^{\ast }$
) values of the dimensionless surfactant concentration with those obtained by Stone & Leal (Reference Stone and Leal1990) and Feigl et al. (Reference Feigl, Megias-Alguacil, Fischer and Windhab2007).
$\unicode[STIX]{x1D713}_{min}^{\ast }$
) values of the dimensionless surfactant concentration with those obtained by Stone & Leal (Reference Stone and Leal1990) and Feigl et al. (Reference Feigl, Megias-Alguacil, Fischer and Windhab2007).
3.2 Droplet deformation in a 2D shear flow
We then apply the hybrid method to simulate the droplet deformation in a 2D shear flow in the presence of surfactants, and compare the numerical results with those obtained from the level-set method (Xu et al.
Reference Xu, Yang and Lowengrub2012). As illustrated in figure 5(a), a circular droplet is initially placed halfway between two parallel walls that are separated by a distance
![]() $H$
. Shear flow is introduced to this system by moving the walls with equal but opposite velocities
$H$
. Shear flow is introduced to this system by moving the walls with equal but opposite velocities
![]() $u_{w}$
, and the resulting shear rate is
$u_{w}$
, and the resulting shear rate is
![]() $\dot{\unicode[STIX]{x1D6FE}}=2u_{w}/H$
. The computational domain is set as
$\dot{\unicode[STIX]{x1D6FE}}=2u_{w}/H$
. The computational domain is set as
![]() $[-5R,5R]\times [-2R,2R]$
, where
$[-5R,5R]\times [-2R,2R]$
, where
![]() $R$
is the initial droplet radius and is taken to be 100 lattices. Periodic boundary conditions are applied in the horizontal direction, while the halfway bounce-back scheme is used on the upper and lower walls. The Langmuir EOS (2.7) is employed, with
$R$
is the initial droplet radius and is taken to be 100 lattices. Periodic boundary conditions are applied in the horizontal direction, while the halfway bounce-back scheme is used on the upper and lower walls. The Langmuir EOS (2.7) is employed, with
![]() $\unicode[STIX]{x1D70E}_{0}=10^{-3}$
and
$\unicode[STIX]{x1D70E}_{0}=10^{-3}$
and
![]() $E_{0}=0.2$
. We run the simulations with
$E_{0}=0.2$
. We run the simulations with
![]() $Ca=0.1$
,
$Ca=0.1$
,
![]() $Re=Pe=10$
and three different values of the surfactant coverage, i.e.
$Re=Pe=10$
and three different values of the surfactant coverage, i.e.
![]() $x_{in}=0$
,
$x_{in}=0$
,
![]() $0.3$
and
$0.3$
and
![]() $0.6$
(it should be noted that
$0.6$
(it should be noted that
![]() $x_{in}=0$
corresponds to the case of a clean droplet).
$x_{in}=0$
corresponds to the case of a clean droplet).
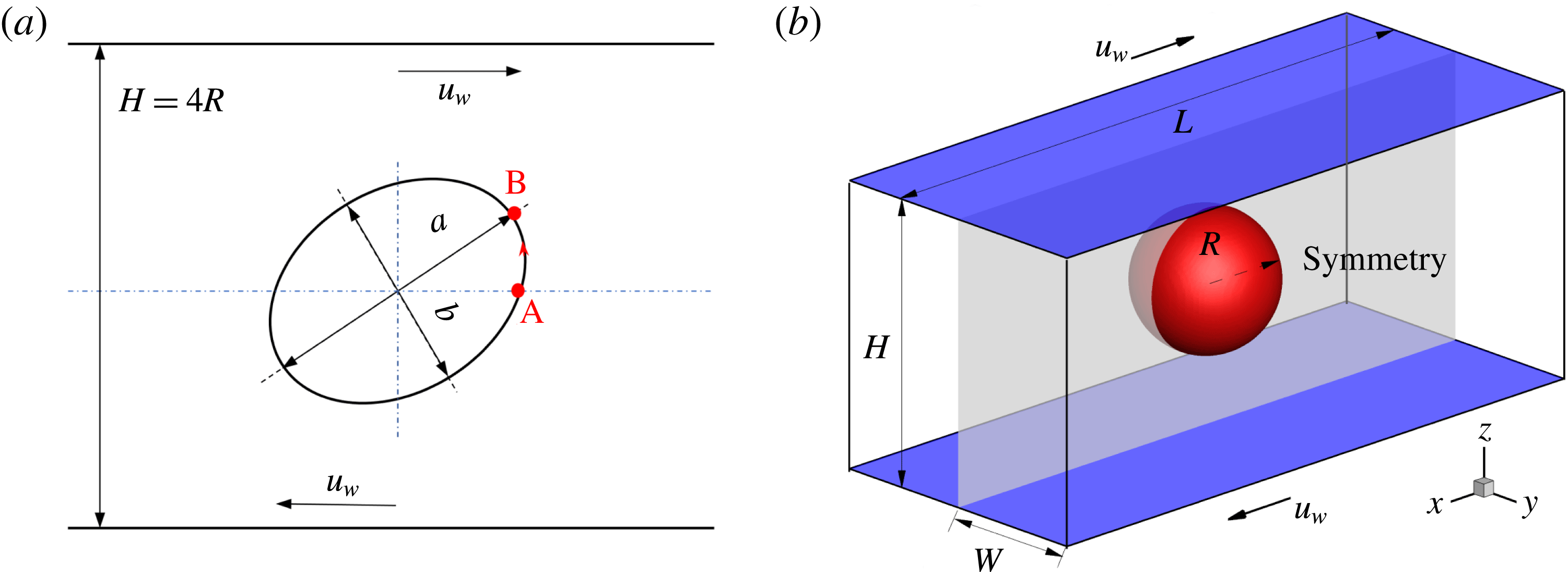
Figure 5. Illustration of (a) a 2D droplet and (b) a 3D droplet in a simple shear flow. In (b), the computational domain is taken as half of the full system, i.e.
![]() $[0,L]\times [0.5,0.5+W]\times [0,H]$
, and the droplet centre is located at
$[0,L]\times [0.5,0.5+W]\times [0,H]$
, and the droplet centre is located at
![]() $(L/2,0.5,H/2)$
.
$(L/2,0.5,H/2)$
.
Figure 6 shows the droplet shapes at
![]() $\unicode[STIX]{x1D70F}=\dot{\unicode[STIX]{x1D6FE}}t=9$
for three different values of
$\unicode[STIX]{x1D70F}=\dot{\unicode[STIX]{x1D6FE}}t=9$
for three different values of
![]() $x_{in}$
, where the
$x_{in}$
, where the
![]() $x$
and
$x$
and
![]() $y$
coordinates are both normalized by the droplet radius
$y$
coordinates are both normalized by the droplet radius
![]() $R$
. Increase in
$R$
. Increase in
![]() $x_{in}$
leads to a more prolate droplet and a decrease of the droplet inclination angle, defined as the angle between the major axis of the droplet and the horizontal (
$x_{in}$
leads to a more prolate droplet and a decrease of the droplet inclination angle, defined as the angle between the major axis of the droplet and the horizontal (
![]() $x$
) axis. Moreover, the droplet shapes obtained by Xu et al. (Reference Xu, Yang and Lowengrub2012) are also plotted in this figure as a comparison, and good agreement is observed for all values of
$x$
) axis. Moreover, the droplet shapes obtained by Xu et al. (Reference Xu, Yang and Lowengrub2012) are also plotted in this figure as a comparison, and good agreement is observed for all values of
![]() $x_{in}$
considered.
$x_{in}$
considered.
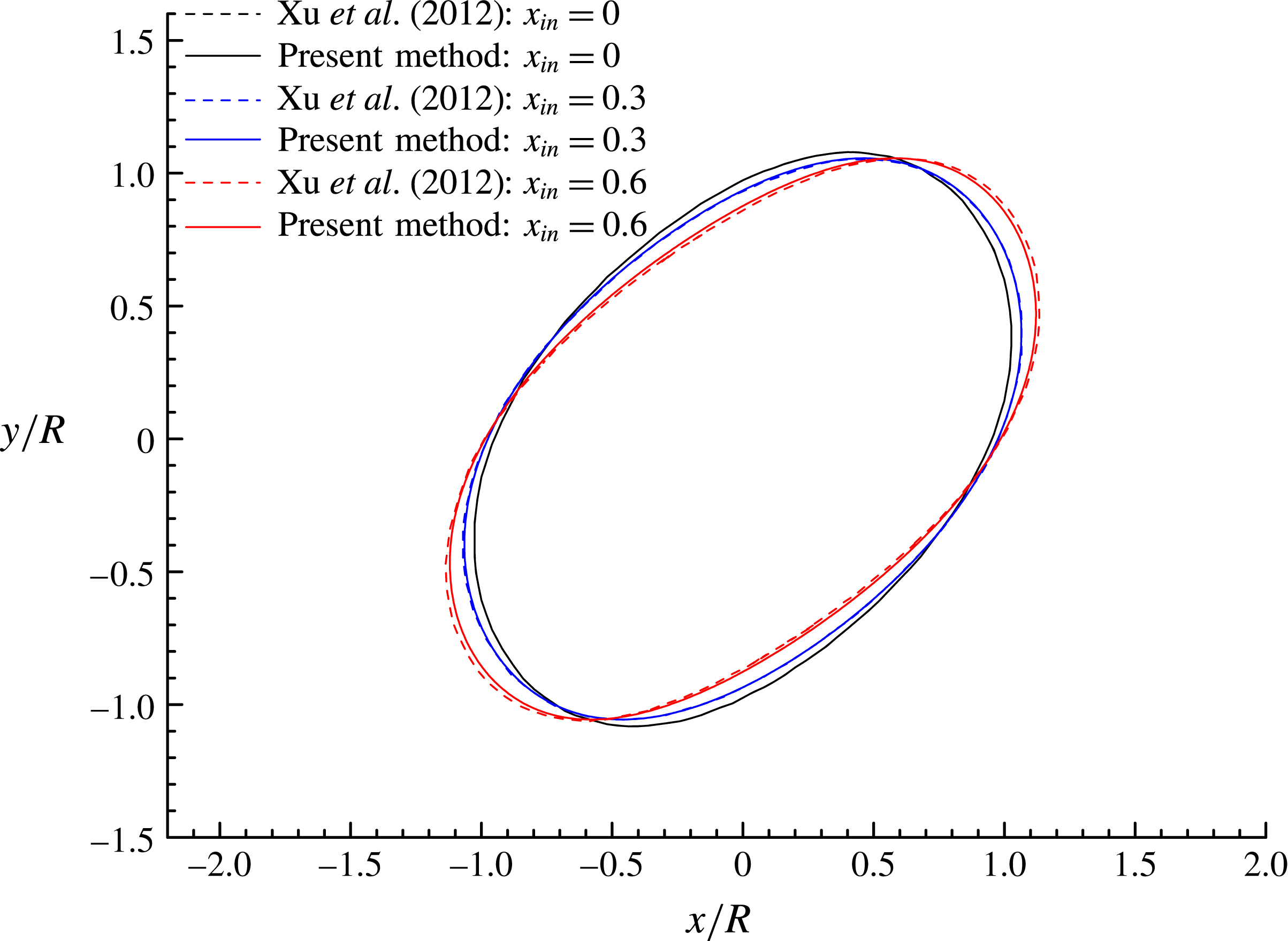
Figure 6. Droplet shapes at
![]() $\unicode[STIX]{x1D70F}=9$
for
$\unicode[STIX]{x1D70F}=9$
for
![]() $x_{in}=0$
,
$x_{in}=0$
,
![]() $0.3$
and
$0.3$
and
![]() $0.6$
. Other parameters are taken as
$0.6$
. Other parameters are taken as
![]() $Re=10$
,
$Re=10$
,
![]() $Pe=10$
,
$Pe=10$
,
![]() $Ca=0.1$
and
$Ca=0.1$
and
![]() $E_{0}=0.2$
. The
$E_{0}=0.2$
. The
![]() $x$
and
$x$
and
![]() $y$
coordinates are both normalized by the droplet radius
$y$
coordinates are both normalized by the droplet radius
![]() $R$
.
$R$
.
Figure 7(a,b) shows the distributions of the dimensionless surfactant concentration
![]() $\unicode[STIX]{x1D713}^{\ast }$
and dimensionless interfacial tension
$\unicode[STIX]{x1D713}^{\ast }$
and dimensionless interfacial tension
![]() $\unicode[STIX]{x1D70E}^{\ast }=\unicode[STIX]{x1D70E}/\unicode[STIX]{x1D70E}_{0}$
along the arclength
$\unicode[STIX]{x1D70E}^{\ast }=\unicode[STIX]{x1D70E}/\unicode[STIX]{x1D70E}_{0}$
along the arclength
![]() $s$
, together with a comparison with those obtained by the level-set method (Xu et al.
Reference Xu, Yang and Lowengrub2012). It should be noted that the arclength
$s$
, together with a comparison with those obtained by the level-set method (Xu et al.
Reference Xu, Yang and Lowengrub2012). It should be noted that the arclength
![]() $s$
, measured counterclockwise from the right intersection point (i.e. the point ‘A’ in figure 5
a) between
$s$
, measured counterclockwise from the right intersection point (i.e. the point ‘A’ in figure 5
a) between
![]() $y=0$
and the droplet interface, is normalized by the initial droplet radius
$y=0$
and the droplet interface, is normalized by the initial droplet radius
![]() $R$
. It is clearly seen that our numerical results agree well with those in Xu et al. (Reference Xu, Yang and Lowengrub2012). Specifically, for the surfactant-covered droplets, i.e.
$R$
. It is clearly seen that our numerical results agree well with those in Xu et al. (Reference Xu, Yang and Lowengrub2012). Specifically, for the surfactant-covered droplets, i.e.
![]() $x_{in}=0.3$
and
$x_{in}=0.3$
and
![]() $0.6$
, we find that
$0.6$
, we find that
![]() $\unicode[STIX]{x1D713}^{\ast }$
is distributed non-uniformly along the interface and tends to accumulate at the droplet tips, resulting in non-uniform distribution of the interfacial tension where the lowest interfacial tension occurs at the droplet tips. In addition, increase in
$\unicode[STIX]{x1D713}^{\ast }$
is distributed non-uniformly along the interface and tends to accumulate at the droplet tips, resulting in non-uniform distribution of the interfacial tension where the lowest interfacial tension occurs at the droplet tips. In addition, increase in
![]() $x_{in}$
decreases the local interfacial tension (see figure 7
b) that resists the movement of the droplet, thereby promoting droplet deformation and reducing the inclination angle.
$x_{in}$
decreases the local interfacial tension (see figure 7
b) that resists the movement of the droplet, thereby promoting droplet deformation and reducing the inclination angle.
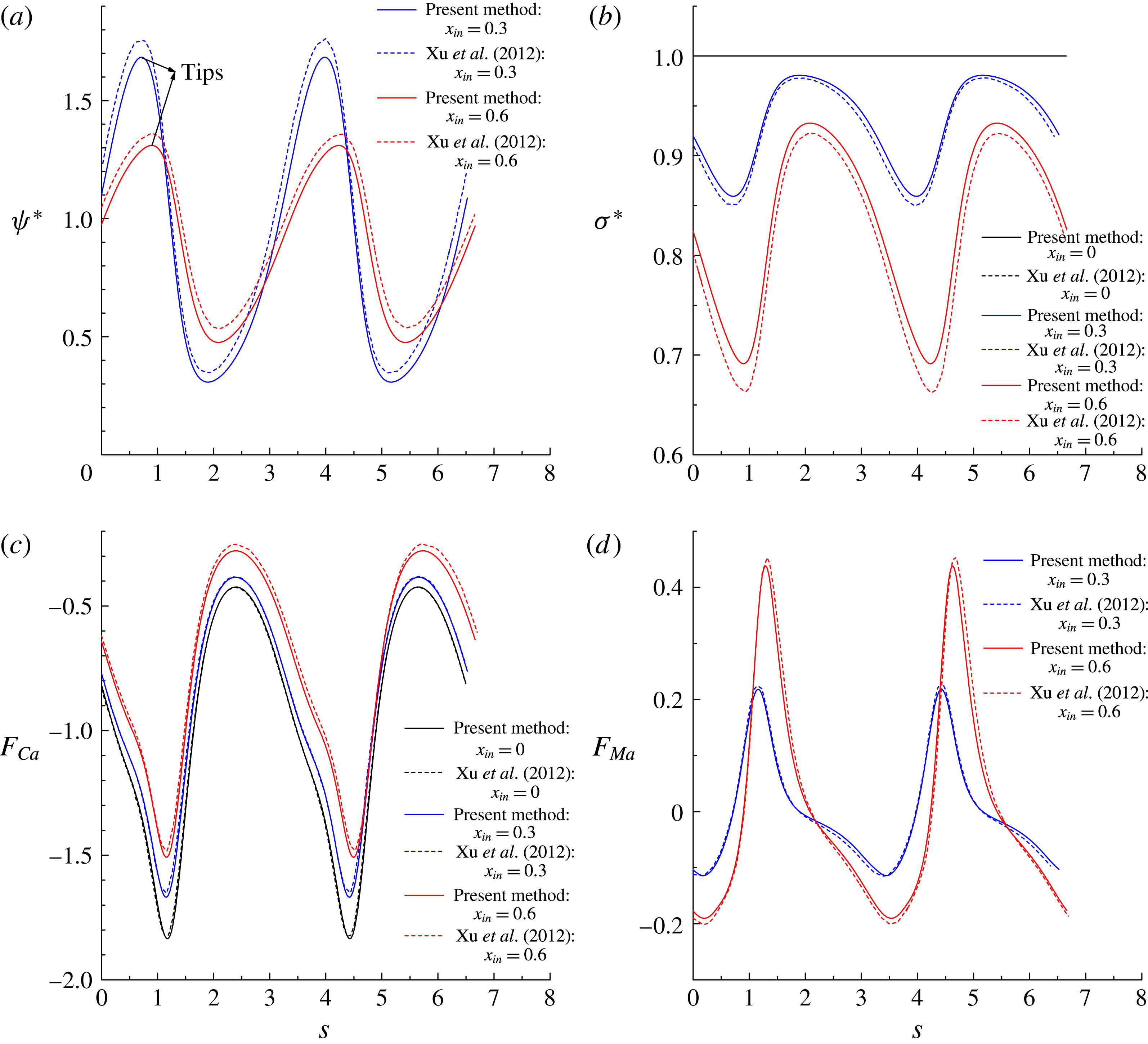
Figure 7. The distributions of (a) the dimensionless surfactant concentration
![]() $\unicode[STIX]{x1D713}^{\ast }$
, (b) the dimensionless interfacial tension
$\unicode[STIX]{x1D713}^{\ast }$
, (b) the dimensionless interfacial tension
![]() $\unicode[STIX]{x1D70E}^{\ast }$
, (c) the signed dimensionless capillary force
$\unicode[STIX]{x1D70E}^{\ast }$
, (c) the signed dimensionless capillary force
![]() $F_{Ca}$
and (d) the signed dimensionless Marangoni force
$F_{Ca}$
and (d) the signed dimensionless Marangoni force
![]() $F_{Ca}$
along the arclength
$F_{Ca}$
along the arclength
![]() $s$
of the interface at
$s$
of the interface at
![]() $\unicode[STIX]{x1D70F}=9$
for
$\unicode[STIX]{x1D70F}=9$
for
![]() $x_{in}=0$
,
$x_{in}=0$
,
![]() $0.3$
and
$0.3$
and
![]() $0.6$
. Other parameters are taken as
$0.6$
. Other parameters are taken as
![]() $Re=10$
,
$Re=10$
,
![]() $Pe=10$
,
$Pe=10$
,
![]() $Ca=0.1$
and
$Ca=0.1$
and
![]() $E_{0}=0.2$
.
$E_{0}=0.2$
.
In figure 7(c,d), we plot the dimensionless capillary force
![]() $F_{Ca}$
and Marangoni force
$F_{Ca}$
and Marangoni force
![]() $F_{Ma}$
as a function of the arclength
$F_{Ma}$
as a function of the arclength
![]() $s$
, where
$s$
, where
![]() $F_{Ca}$
and
$F_{Ca}$
and
![]() $F_{Ma}$
are calculated by
$F_{Ma}$
are calculated by
![]() $\unicode[STIX]{x1D705}\unicode[STIX]{x1D70E}^{\ast }R$
and
$\unicode[STIX]{x1D705}\unicode[STIX]{x1D70E}^{\ast }R$
and
![]() $\unicode[STIX]{x1D735}_{s}\unicode[STIX]{x1D70E}^{\ast }\boldsymbol{\cdot }\boldsymbol{\unicode[STIX]{x1D70F}}R$
with the unit tangential vector
$\unicode[STIX]{x1D735}_{s}\unicode[STIX]{x1D70E}^{\ast }\boldsymbol{\cdot }\boldsymbol{\unicode[STIX]{x1D70F}}R$
with the unit tangential vector
![]() $\boldsymbol{\unicode[STIX]{x1D70F}}=(-n_{y},n_{x})$
. It can be observed that the distributions of
$\boldsymbol{\unicode[STIX]{x1D70F}}=(-n_{y},n_{x})$
. It can be observed that the distributions of
![]() $F_{Ca}$
and
$F_{Ca}$
and
![]() $F_{Ma}$
are in excellent agreement with the numerical results of Xu et al. (Reference Xu, Yang and Lowengrub2012). Along the arclength,
$F_{Ma}$
are in excellent agreement with the numerical results of Xu et al. (Reference Xu, Yang and Lowengrub2012). Along the arclength,
![]() $F_{Ca}$
reaches its maximum value at the droplet tips due to the high interface curvature, and increase of
$F_{Ca}$
reaches its maximum value at the droplet tips due to the high interface curvature, and increase of
![]() $x_{in}$
decreases the absolute value of the capillary force. The Marangoni force arises due to the non-uniform distribution of
$x_{in}$
decreases the absolute value of the capillary force. The Marangoni force arises due to the non-uniform distribution of
![]() $\unicode[STIX]{x1D70E}^{\ast }$
. It acts in the tangential direction of the interface, and is directed from higher to lower
$\unicode[STIX]{x1D70E}^{\ast }$
. It acts in the tangential direction of the interface, and is directed from higher to lower
![]() $\unicode[STIX]{x1D713}^{\ast }$
regions, resisting the accumulation of surfactants (or, say, lowering the non-uniformity of the surfactant distribution). In figure 7(d), we find that
$\unicode[STIX]{x1D713}^{\ast }$
regions, resisting the accumulation of surfactants (or, say, lowering the non-uniformity of the surfactant distribution). In figure 7(d), we find that
![]() $F_{Ma}$
is zero at the droplet tips due to symmetry, and takes its local maximum and minimum values near the tips because of the highest gradient of
$F_{Ma}$
is zero at the droplet tips due to symmetry, and takes its local maximum and minimum values near the tips because of the highest gradient of
![]() $\unicode[STIX]{x1D70E}^{\ast }$
in these regions. It is also noticed that the amplitude of
$\unicode[STIX]{x1D70E}^{\ast }$
in these regions. It is also noticed that the amplitude of
![]() $F_{Ma}$
increases with increasing
$F_{Ma}$
increases with increasing
![]() $x_{in}$
from 0.3 to 0.6.
$x_{in}$
from 0.3 to 0.6.
4 Deformation and breakup of a droplet in a 3D shear flow
Having validated the hybrid LB–FD method, we investigate the influence of surfactants on the droplet deformation and breakup in a 3D shear flow. As depicted in figure 5(b), a 3D droplet (red fluid) with radius
![]() $R$
is initially placed in the centre of two plates, both parallel to the
$R$
is initially placed in the centre of two plates, both parallel to the
![]() $x$
–
$x$
–
![]() $y$
plane at distance
$y$
plane at distance
![]() $H$
apart. The two plates move at equal speeds of
$H$
apart. The two plates move at equal speeds of
![]() $u_{w}$
but in opposite directions, thereby creating a linear shear flow with a shear rate of
$u_{w}$
but in opposite directions, thereby creating a linear shear flow with a shear rate of
![]() $\dot{\unicode[STIX]{x1D6FE}}=2u_{w}/H$
. Periodic boundary conditions are applied in the
$\dot{\unicode[STIX]{x1D6FE}}=2u_{w}/H$
. Periodic boundary conditions are applied in the
![]() $x$
-direction, while halfway bounce-back boundary conditions are imposed on the top and bottom walls with constant velocities of
$x$
-direction, while halfway bounce-back boundary conditions are imposed on the top and bottom walls with constant velocities of
![]() $(u_{w},0,0)$
and
$(u_{w},0,0)$
and
![]() $(-u_{w},0,0)$
, respectively. Due to symmetry, only half of the flow domain in the
$(-u_{w},0,0)$
, respectively. Due to symmetry, only half of the flow domain in the
![]() $y$
-direction is considered. Assuming that the symmetric boundary is positioned at
$y$
-direction is considered. Assuming that the symmetric boundary is positioned at
![]() $y=0.5$
, we place an extra grid layer at
$y=0.5$
, we place an extra grid layer at
![]() $y=0$
to facilitate the implementation of a symmetric boundary condition. For the distribution functions, symmetry is achieved by setting
$y=0$
to facilitate the implementation of a symmetric boundary condition. For the distribution functions, symmetry is achieved by setting
![]() $f_{i^{\ast }}^{k\ddagger }(x,0,z)=f_{i}^{k\ddagger }(x,1,z)$
before the propagation step, where
$f_{i^{\ast }}^{k\ddagger }(x,0,z)=f_{i}^{k\ddagger }(x,1,z)$
before the propagation step, where
![]() $\boldsymbol{e}_{i^{\ast }}=\boldsymbol{e}_{i}-2(\boldsymbol{e}_{i}\boldsymbol{\cdot }\bar{\boldsymbol{n}})\bar{\boldsymbol{n}}$
, with
$\boldsymbol{e}_{i^{\ast }}=\boldsymbol{e}_{i}-2(\boldsymbol{e}_{i}\boldsymbol{\cdot }\bar{\boldsymbol{n}})\bar{\boldsymbol{n}}$
, with
![]() $\bar{\boldsymbol{n}}=(0,1,0)$
. Besides, the symmetry requires that
$\bar{\boldsymbol{n}}=(0,1,0)$
. Besides, the symmetry requires that
![]() $\unicode[STIX]{x1D719}(x,0,z)=\unicode[STIX]{x1D719}(x,1,z)$
for a scalar
$\unicode[STIX]{x1D719}(x,0,z)=\unicode[STIX]{x1D719}(x,1,z)$
for a scalar
![]() $\unicode[STIX]{x1D719}$
and
$\unicode[STIX]{x1D719}$
and
![]() $v_{x}(x,0,z)=v_{x}(x,1,z)$
,
$v_{x}(x,0,z)=v_{x}(x,1,z)$
,
![]() $v_{y}(x,0,z)=-v_{y}(x,1,z)$
,
$v_{y}(x,0,z)=-v_{y}(x,1,z)$
,
![]() $v_{z}(x,0,z)=v_{z}(x,1,z)$
for a vector
$v_{z}(x,0,z)=v_{z}(x,1,z)$
for a vector
![]() $\boldsymbol{v}$
. Throughout this section, both fluids are of equal density and equal viscosity, with their values depending on the specific flow conditions. The Langmuir equation (2.6) is employed to relate the interfacial tension to the surfactant concentration, in which the interfacial tension of a clean interface is taken as
$\boldsymbol{v}$
. Throughout this section, both fluids are of equal density and equal viscosity, with their values depending on the specific flow conditions. The Langmuir equation (2.6) is employed to relate the interfacial tension to the surfactant concentration, in which the interfacial tension of a clean interface is taken as
![]() $\unicode[STIX]{x1D70E}_{0}=10^{-3}$
and the elasticity number is
$\unicode[STIX]{x1D70E}_{0}=10^{-3}$
and the elasticity number is
![]() $E_{0}=0.5$
.
$E_{0}=0.5$
.
4.1 Droplet deformation
For a clean droplet in the Stokes flow regime, Taylor (Reference Taylor1934) derived a theoretical formula for the small deformation in the shear flow in terms of the viscosity ratio
![]() $\unicode[STIX]{x1D706}$
(
$\unicode[STIX]{x1D706}$
(
![]() $\unicode[STIX]{x1D706}=\unicode[STIX]{x1D707}^{R}/\unicode[STIX]{x1D707}^{B}$
) and the capillary number,
$\unicode[STIX]{x1D706}=\unicode[STIX]{x1D707}^{R}/\unicode[STIX]{x1D707}^{B}$
) and the capillary number,
However, the prediction of Taylor does not consider the proximity of the droplet to the walls, i.e. the confinement ratio, defined as the ratio between the droplet diameter
![]() $2R$
and the wall separation
$2R$
and the wall separation
![]() $H$
(
$H$
(
![]() $2R/H$
). When the confinement ratio is higher than 0.4, the deformation cannot be predicted accurately by (4.1). Moreover, (4.1) is not able to describe the droplet deformation for very large viscosity ratios (Vananroye, Van Puyvelde & Moldenaers Reference Vananroye, Van Puyvelde and Moldenaers2007). More discussion about this equation can be found in several review papers (Cristini & Tan Reference Cristini and Tan2004; Guido & Greco Reference Guido and Greco2004; Puyvelde et al.
Reference Puyvelde, Vananroye, Cardinaels and Moldenaers2008; Minale Reference Minale2010).
$2R/H$
). When the confinement ratio is higher than 0.4, the deformation cannot be predicted accurately by (4.1). Moreover, (4.1) is not able to describe the droplet deformation for very large viscosity ratios (Vananroye, Van Puyvelde & Moldenaers Reference Vananroye, Van Puyvelde and Moldenaers2007). More discussion about this equation can be found in several review papers (Cristini & Tan Reference Cristini and Tan2004; Guido & Greco Reference Guido and Greco2004; Puyvelde et al.
Reference Puyvelde, Vananroye, Cardinaels and Moldenaers2008; Minale Reference Minale2010).
To address the influence of the confinement ratio, a number of theoretical or phenomenological models have been proposed to predict the deformation parameter. For instance, Shapira & Haber (Reference Shapira and Haber1990) provided a new expression that combines the Taylor deformation and an additional term accounting for the wall effects, and Maffettone & Minale (Reference Maffettone and Minale1998) proposed a phenomenological model to predict the droplet deformation under transient conditions. Later, Vananroye et al. (Reference Vananroye, Van Puyvelde and Moldenaers2007) developed the so-called MMSH model, in which the model of Shapira & Haber (Reference Shapira and Haber1990) is modified by replacing the Taylor model with the model of Maffettone & Minale (Reference Maffettone and Minale1998) as bulk reference. Vananroye et al. (Reference Vananroye, Van Puyvelde and Moldenaers2007) found that the droplet behaviour can be reasonably predicted by the MMSH model for a wide range of viscosity ratios and confinement ratios, and for
![]() $Ca\leqslant 0.3$
. The MMSH model is given by
$Ca\leqslant 0.3$
. The MMSH model is given by
with
where
and
![]() $C_{s}$
is a shape parameter, which is taken as
$C_{s}$
is a shape parameter, which is taken as
![]() $5.6996$
for a droplet positioned halfway between two plates.
$5.6996$
for a droplet positioned halfway between two plates.
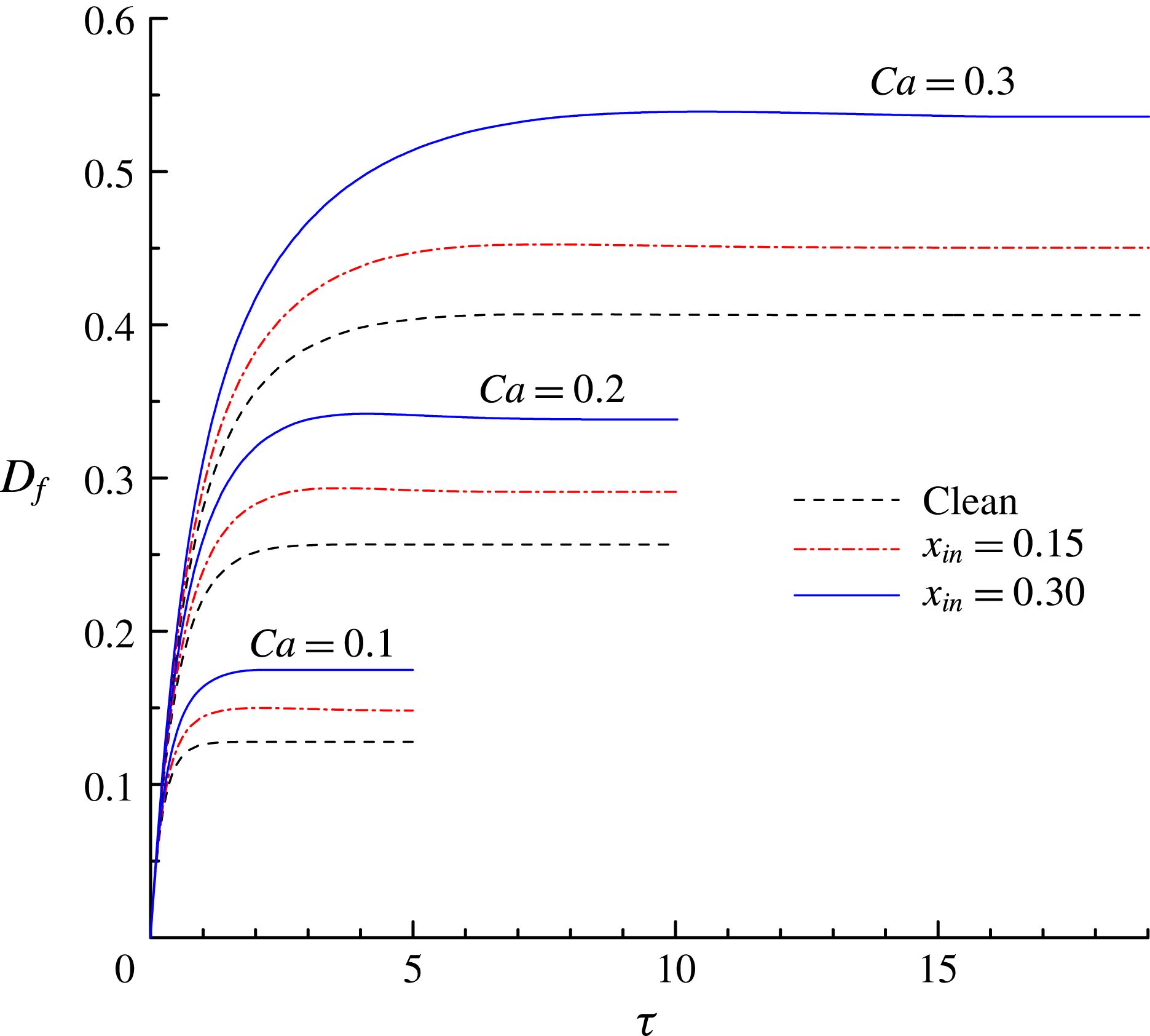
Figure 8. The time evolution of the deformation parameter
![]() $D_{f}$
for
$D_{f}$
for
![]() $x_{in}=0$
, 0.15 and 0.3 at
$x_{in}=0$
, 0.15 and 0.3 at
![]() $Ca=0.1$
, 0.2 and 0.3.
$Ca=0.1$
, 0.2 and 0.3.
In our numerical simulation, the initial droplet radius is
![]() $R=25$
, and the domain height and width are
$R=25$
, and the domain height and width are
![]() $H=100$
and
$H=100$
and
![]() $W=50$
respectively, so that the confinement ratio is
$W=50$
respectively, so that the confinement ratio is
![]() $2R/H=0.5$
. The simulations are run in a
$2R/H=0.5$
. The simulations are run in a
![]() $200\times 50\times 100$
lattice domain for the capillary number ranging from 0.05 to 0.3 at
$200\times 50\times 100$
lattice domain for the capillary number ranging from 0.05 to 0.3 at
![]() $Re=0.1$
, which is small enough to meet the Stokes flow condition. Three different values of the surfactant coverage are considered, i.e.
$Re=0.1$
, which is small enough to meet the Stokes flow condition. Three different values of the surfactant coverage are considered, i.e.
![]() $x_{in}=0$
,
$x_{in}=0$
,
![]() $0.15$
and
$0.15$
and
![]() $0.3$
. Figure 8 shows the time evolution of the deformation parameter
$0.3$
. Figure 8 shows the time evolution of the deformation parameter
![]() $D_{f}$
at
$D_{f}$
at
![]() $Pe=10$
for
$Pe=10$
for
![]() $Ca=0.1,0.2$
and
$Ca=0.1,0.2$
and
![]() $0.3$
. It is observed that
$0.3$
. It is observed that
![]() $D_{f}$
first increases and then evolves to a steady value for each of the cases considered. For a fixed surfactant coverage
$D_{f}$
first increases and then evolves to a steady value for each of the cases considered. For a fixed surfactant coverage
![]() $x_{in}$
,
$x_{in}$
,
![]() $D_{f}$
increases with
$D_{f}$
increases with
![]() $Ca$
, and for a constant
$Ca$
, and for a constant
![]() $Ca$
,
$Ca$
,
![]() $D_{f}$
increases with
$D_{f}$
increases with
![]() $x_{in}$
. In addition, the droplet takes a longer time to achieve a steady shape for higher
$x_{in}$
. In addition, the droplet takes a longer time to achieve a steady shape for higher
![]() $Ca$
or
$Ca$
or
![]() $x_{in}$
.
$x_{in}$
.
In figure 9, we present the variation of the deformation parameter with
![]() $Ca$
for the cases of clean droplet, surfactant-laden droplet, and clean droplet with reduced interfacial tension
$Ca$
for the cases of clean droplet, surfactant-laden droplet, and clean droplet with reduced interfacial tension
![]() $\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70E}_{0}/[1+E_{0}\ln (1-x_{in})]$
, and their corresponding deformation parameters are denoted as
$\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70E}_{0}/[1+E_{0}\ln (1-x_{in})]$
, and their corresponding deformation parameters are denoted as
![]() $D_{f0}$
,
$D_{f0}$
,
![]() $D_{f2}$
and
$D_{f2}$
and
![]() $D_{f1}$
for the convenience of subsequent discussion. Predictions from the MMSH model are also plotted as a comparison. It can be seen that our simulation results concerning the clean droplet agree well with the predictions from the MMSH model, suggesting that the present method is able to accurately simulate the deformation of a clean droplet in simple shear flows. The presence of the surfactants increases the droplet deformation for all values of
$D_{f1}$
for the convenience of subsequent discussion. Predictions from the MMSH model are also plotted as a comparison. It can be seen that our simulation results concerning the clean droplet agree well with the predictions from the MMSH model, suggesting that the present method is able to accurately simulate the deformation of a clean droplet in simple shear flows. The presence of the surfactants increases the droplet deformation for all values of
![]() $Ca$
. The increased deformation, i.e.
$Ca$
. The increased deformation, i.e.
![]() $D_{f2}-D_{f0}$
, consists of two parts: (1)
$D_{f2}-D_{f0}$
, consists of two parts: (1)
![]() $\unicode[STIX]{x1D6FF}_{1}=D_{f1}-D_{f0}$
, which is attributed to a reduction of the interfacial tension caused by the average surfactant concentration
$\unicode[STIX]{x1D6FF}_{1}=D_{f1}-D_{f0}$
, which is attributed to a reduction of the interfacial tension caused by the average surfactant concentration
![]() $\unicode[STIX]{x1D713}_{0}$
, and (2)
$\unicode[STIX]{x1D713}_{0}$
, and (2)
![]() $\unicode[STIX]{x1D6FF}_{2}=D_{f2}-D_{f1}$
, which is attributed to the non-uniform effects from non-uniform capillary pressure on the droplet surface and Marangoni stresses along the interface. As can be clearly seen from the inset of figure 9,
$\unicode[STIX]{x1D6FF}_{2}=D_{f2}-D_{f1}$
, which is attributed to the non-uniform effects from non-uniform capillary pressure on the droplet surface and Marangoni stresses along the interface. As can be clearly seen from the inset of figure 9,
![]() $\unicode[STIX]{x1D6FF}_{1}$
accounts for most of the effect of surfactants on the droplet deformation, and increases with
$\unicode[STIX]{x1D6FF}_{1}$
accounts for most of the effect of surfactants on the droplet deformation, and increases with
![]() $Ca$
. On the other hand, as
$Ca$
. On the other hand, as
![]() $Ca$
increases,
$Ca$
increases,
![]() $\unicode[STIX]{x1D6FF}_{2}$
first increases and then decreases, with its maximum value occurring at
$\unicode[STIX]{x1D6FF}_{2}$
first increases and then decreases, with its maximum value occurring at
![]() $Ca=0.15$
. The reason may be that as
$Ca=0.15$
. The reason may be that as
![]() $Ca$
increases, the dilution of the surfactants becomes increasingly significant, which weakens the non-uniform effects.
$Ca$
increases, the dilution of the surfactants becomes increasingly significant, which weakens the non-uniform effects.
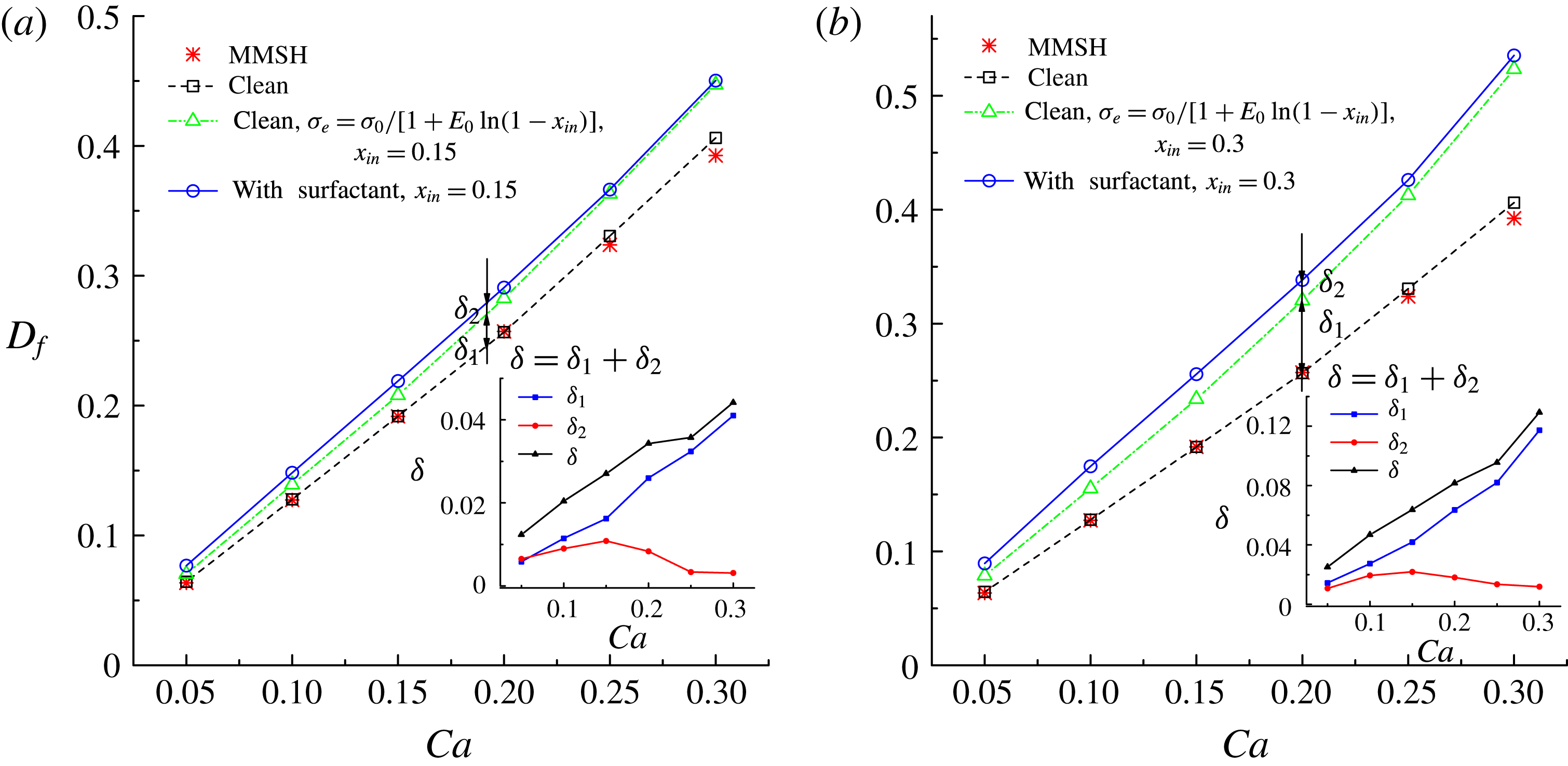
Figure 9. The deformation parameter
![]() $D_{f}$
as a function of
$D_{f}$
as a function of
![]() $Ca$
for the clean droplet, the surfactant-laden droplet, and the clean droplet with the reduced interfacial tension
$Ca$
for the clean droplet, the surfactant-laden droplet, and the clean droplet with the reduced interfacial tension
![]() $\unicode[STIX]{x1D70E}_{e}=\unicode[STIX]{x1D70E}_{0}/[1+E_{0}\ln (1-x_{in})]$
at (a)
$\unicode[STIX]{x1D70E}_{e}=\unicode[STIX]{x1D70E}_{0}/[1+E_{0}\ln (1-x_{in})]$
at (a)
![]() $x_{in}=0.15$
and (b)
$x_{in}=0.15$
and (b)
![]() $x_{in}=0.3$
. The predictions from the MMSH model are also shown for comparison. The inset plots the increment of the deformation parameter
$x_{in}=0.3$
. The predictions from the MMSH model are also shown for comparison. The inset plots the increment of the deformation parameter
![]() $\unicode[STIX]{x1D6FF}$
(due to the presence of surfactants) and its two constituents
$\unicode[STIX]{x1D6FF}$
(due to the presence of surfactants) and its two constituents
![]() $\unicode[STIX]{x1D6FF}_{1}$
and
$\unicode[STIX]{x1D6FF}_{1}$
and
![]() $\unicode[STIX]{x1D6FF}_{2}$
as a function of
$\unicode[STIX]{x1D6FF}_{2}$
as a function of
![]() $Ca$
.
$Ca$
.
The surface Péclet number
![]() $Pe$
is an important parameter which affects the non-uniform distribution of surfactants, and here we take
$Pe$
is an important parameter which affects the non-uniform distribution of surfactants, and here we take
![]() $Pe$
ranging from 0.1 to 10 to investigate the effect of
$Pe$
ranging from 0.1 to 10 to investigate the effect of
![]() $Pe$
on the droplet deformation. Different values of
$Pe$
on the droplet deformation. Different values of
![]() $Pe$
are achieved by varying
$Pe$
are achieved by varying
![]() $D_{s}$
while keeping other parameters unchanged. In figure 10, we plot the deformation parameter
$D_{s}$
while keeping other parameters unchanged. In figure 10, we plot the deformation parameter
![]() $D_{f}$
, and the
$D_{f}$
, and the
![]() $\unicode[STIX]{x1D713}_{min}$
and
$\unicode[STIX]{x1D713}_{min}$
and
![]() $\unicode[STIX]{x1D713}_{max}$
values of the surfactant concentration at
$\unicode[STIX]{x1D713}_{max}$
values of the surfactant concentration at
![]() $\unicode[STIX]{x1D70C}^{N}=0$
as a function of
$\unicode[STIX]{x1D70C}^{N}=0$
as a function of
![]() $Pe$
for
$Pe$
for
![]() $Ca=0.15$
and
$Ca=0.15$
and
![]() $x_{in}=0.3$
. It is observed that the difference between
$x_{in}=0.3$
. It is observed that the difference between
![]() $\unicode[STIX]{x1D713}_{max}$
and
$\unicode[STIX]{x1D713}_{max}$
and
![]() $\unicode[STIX]{x1D713}_{min}$
increases with
$\unicode[STIX]{x1D713}_{min}$
increases with
![]() $Pe$
, which indicates an enhanced non-uniformity of the surfactant distribution. This non-uniformity leads to a larger
$Pe$
, which indicates an enhanced non-uniformity of the surfactant distribution. This non-uniformity leads to a larger
![]() $\unicode[STIX]{x1D6FF}_{2}$
, and thus an enhanced droplet deformation, as shown in figure 10(a).
$\unicode[STIX]{x1D6FF}_{2}$
, and thus an enhanced droplet deformation, as shown in figure 10(a).
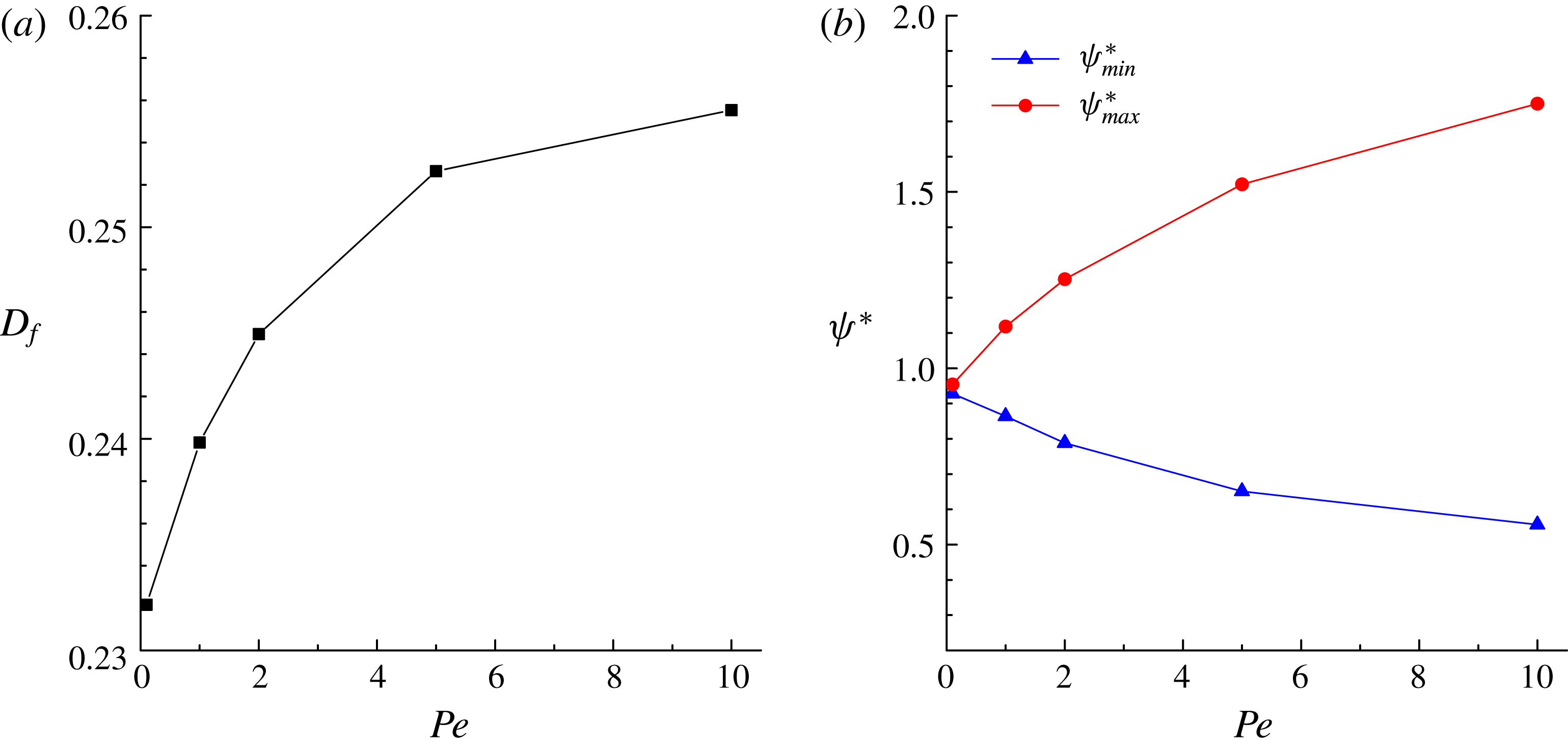
Figure 10. (a) The deformation parameter
![]() $D_{f}$
and (b) the minimum and maximum values of the surfactant concentration on the interface (
$D_{f}$
and (b) the minimum and maximum values of the surfactant concentration on the interface (
![]() $\unicode[STIX]{x1D70C}^{N}=0$
) for various values of
$\unicode[STIX]{x1D70C}^{N}=0$
) for various values of
![]() $Pe$
at
$Pe$
at
![]() $Ca=0.15$
and
$Ca=0.15$
and
![]() $x_{in}=0.3$
.
$x_{in}=0.3$
.
As pointed out in § 1, the Marangoni stress term was not explicitly considered by Farhat et al. (Reference Farhat, Celiker, Singh and Lee2011) in the modelling of interfacial flows with insoluble surfactants. To show the effect of neglecting the Marangoni stress on the droplet behaviour, we run the simulation with the Marangoni stress turned off for
![]() $Ca=0.1$
,
$Ca=0.1$
,
![]() $Re=0.1$
,
$Re=0.1$
,
![]() $Pe=10$
and
$Pe=10$
and
![]() $x_{in}=0.15$
, and compare the simulated results with those obtained when the Marangoni stress is included. Figure 11 shows the final droplet shapes and surfactant concentration distributions on the interface (
$x_{in}=0.15$
, and compare the simulated results with those obtained when the Marangoni stress is included. Figure 11 shows the final droplet shapes and surfactant concentration distributions on the interface (
![]() $\unicode[STIX]{x1D70C}^{N}=0$
) for the surfactant-laden cases with and without Marangoni stresses. It can be seen that neglect of the Marangoni stress leads to more surfactants distributed in the tip regions of the droplet, which cause a decrease in interfacial tension and thus a larger droplet deformation. Specifically, the deformation parameter is
$\unicode[STIX]{x1D70C}^{N}=0$
) for the surfactant-laden cases with and without Marangoni stresses. It can be seen that neglect of the Marangoni stress leads to more surfactants distributed in the tip regions of the droplet, which cause a decrease in interfacial tension and thus a larger droplet deformation. Specifically, the deformation parameter is
![]() $D_{f}=0.148$
in the case with Marangoni stress, which is increased to
$D_{f}=0.148$
in the case with Marangoni stress, which is increased to
![]() $D_{f}=0.169$
when the Marangoni stress is turned off. However, it should be noted that, physically, the Marangoni stress will arise spontaneously as long as there exists an interfacial tension gradient (which can be caused by a concentration gradient or a temperature gradient), and neglect of the Marangoni stress in numerical modelling could lead to significant errors or even incorrect droplet behaviour when a spatially varying interfacial tension is considered (Sui Reference Sui2014).
$D_{f}=0.169$
when the Marangoni stress is turned off. However, it should be noted that, physically, the Marangoni stress will arise spontaneously as long as there exists an interfacial tension gradient (which can be caused by a concentration gradient or a temperature gradient), and neglect of the Marangoni stress in numerical modelling could lead to significant errors or even incorrect droplet behaviour when a spatially varying interfacial tension is considered (Sui Reference Sui2014).
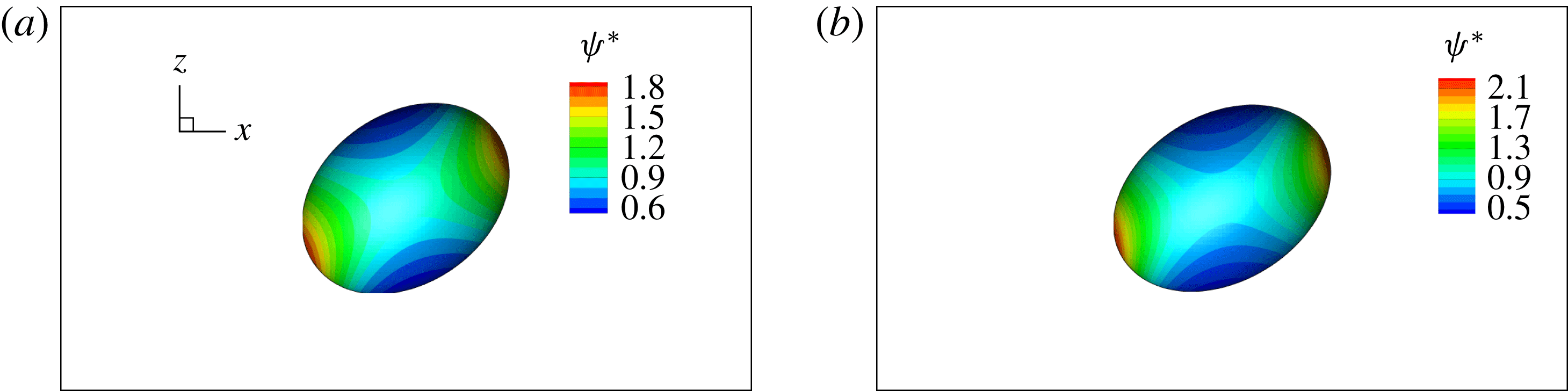
Figure 11. Droplet shapes and surfactant concentration distributions at
![]() $Ca=0.1$
,
$Ca=0.1$
,
![]() $Re=0.1$
,
$Re=0.1$
,
![]() $Pe=10$
and
$Pe=10$
and
![]() $x_{in}=0.15$
for the surfactant-laden cases (a) with and (b) without Marangoni stresses.
$x_{in}=0.15$
for the surfactant-laden cases (a) with and (b) without Marangoni stresses.
4.2 Droplet breakup
A large number of studies (Pathak & Migler Reference Pathak and Migler2003; Sibillo et al.
Reference Sibillo, Pasquariello, Simeone, Cristini and Guido2006; Renardy Reference Renardy2007; Janssen et al.
Reference Janssen, Vananroye, Van Puyvelde, Moldenaers and Anderson2010) have indicated that in the case of a clean droplet, there usually exists a critical capillary number
![]() $Ca_{cr}$
, above which the droplet continuously deforms without reaching a steady state and finally breaks up into daughter droplets. It has been experimentally and numerically recognized that
$Ca_{cr}$
, above which the droplet continuously deforms without reaching a steady state and finally breaks up into daughter droplets. It has been experimentally and numerically recognized that
![]() $Ca_{cr}$
is a function of the confinement ratio and the viscosity ratio in the Stokes flow regime. Here, we investigate the critical capillary number of droplet breakup at a constant viscosity ratio of unity for varying confinement ratios and Reynolds numbers. The domain width is fixed at
$Ca_{cr}$
is a function of the confinement ratio and the viscosity ratio in the Stokes flow regime. Here, we investigate the critical capillary number of droplet breakup at a constant viscosity ratio of unity for varying confinement ratios and Reynolds numbers. The domain width is fixed at
![]() $4R$
with the droplet radius set as
$4R$
with the droplet radius set as
![]() $R=30$
. The domain height varies with the confinement ratio, and the domain length is set to be at least
$R=30$
. The domain height varies with the confinement ratio, and the domain length is set to be at least
![]() $10R$
in order to avoid the occurrence that the droplet touches itself via the periodic boundary conditions before breakup.
$10R$
in order to avoid the occurrence that the droplet touches itself via the periodic boundary conditions before breakup.
4.2.1 Influence of the capillary number and confinement ratio
First, the critical capillary number for the breakup of a clean droplet is studied for
![]() $Re=0.1$
with confinement ratios ranging from 0.3 to 0.85. As previously done by Janssen et al. (Reference Janssen, Vananroye, Van Puyvelde, Moldenaers and Anderson2010), we define the critical capillary number (
$Re=0.1$
with confinement ratios ranging from 0.3 to 0.85. As previously done by Janssen et al. (Reference Janssen, Vananroye, Van Puyvelde, Moldenaers and Anderson2010), we define the critical capillary number (
![]() $Ca_{cr}$
) as the lowest capillary number found at which an initially spherical droplet breaks up. For each confinement ratio, the ‘lowest’ capillary number is found by increasing
$Ca_{cr}$
) as the lowest capillary number found at which an initially spherical droplet breaks up. For each confinement ratio, the ‘lowest’ capillary number is found by increasing
![]() $Ca$
with an increment of
$Ca$
with an increment of
![]() $0.02$
or lower from a case where the droplet does not break up. Figure 12 illustrates the simulation results of our hybrid method along with the experimental and numerical results of Janssen et al. (Reference Janssen, Vananroye, Van Puyvelde, Moldenaers and Anderson2010). In the figure, we use discrete symbols without a ‘+’ to denote the binary breakup (see, e.g., figure 13
b) and discrete symbols with a ‘+’ to denote the ternary breakup, where the droplet splits into three daughter droplets (see, e.g., figure 13
c).
$0.02$
or lower from a case where the droplet does not break up. Figure 12 illustrates the simulation results of our hybrid method along with the experimental and numerical results of Janssen et al. (Reference Janssen, Vananroye, Van Puyvelde, Moldenaers and Anderson2010). In the figure, we use discrete symbols without a ‘+’ to denote the binary breakup (see, e.g., figure 13
b) and discrete symbols with a ‘+’ to denote the ternary breakup, where the droplet splits into three daughter droplets (see, e.g., figure 13
c).

Figure 12. The critical capillary number of droplet breakup as a function of the confinement ratio in surfactant-free and surfactant-laden systems. Binary and ternary breakups are represented by the discrete symbols without a ‘+’ and the discrete symbols with a ‘+’ respectively. The experimental and BIM simulation results for clean droplets are taken from Janssen et al. (Reference Janssen, Vananroye, Van Puyvelde, Moldenaers and Anderson2010).
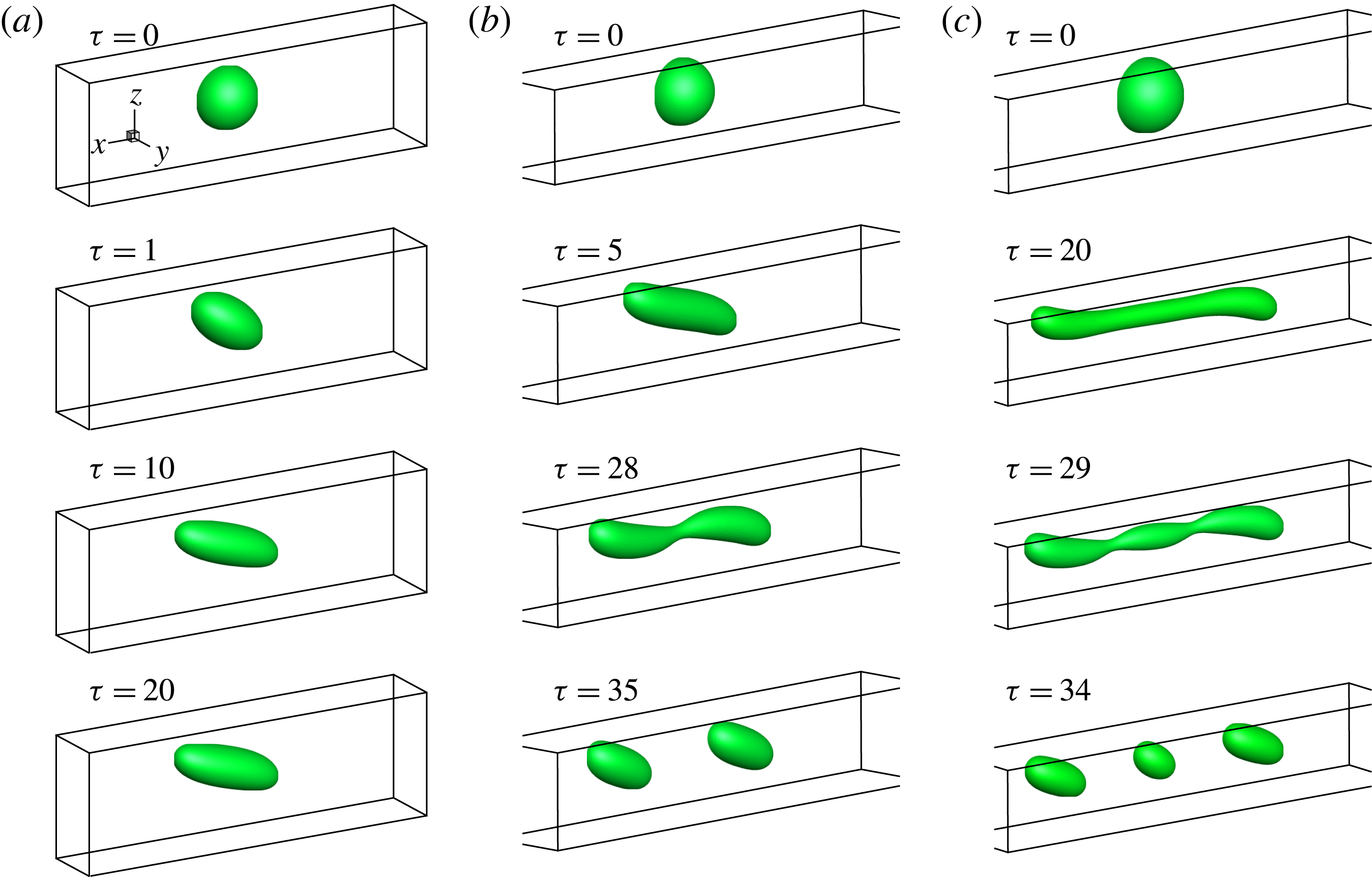
Figure 13. Snapshots of the droplet shape at
![]() $Re=0.1$
for (a)
$Re=0.1$
for (a)
![]() $Ca=0.35$
,
$Ca=0.35$
,
![]() $2R/H=0.5$
, (b)
$2R/H=0.5$
, (b)
![]() $Ca=0.415$
,
$Ca=0.415$
,
![]() $2R/H=0.7$
and (c)
$2R/H=0.7$
and (c)
![]() $Ca=0.46$
,
$Ca=0.46$
,
![]() $2R/H=0.8$
for the clean droplets.
$2R/H=0.8$
for the clean droplets.
As shown in figure 12, the simulated critical capillary number is varied from
![]() $0.415$
at
$0.415$
at
![]() $2R/H=0.3$
and
$2R/H=0.3$
and
![]() $0.4$
, to
$0.4$
, to
![]() $0.392$
at
$0.392$
at
![]() $2R/H=0.5$
, then to
$2R/H=0.5$
, then to
![]() $0.395$
at
$0.395$
at
![]() $2R/H=0.6$
, next to
$2R/H=0.6$
, next to
![]() $0.415$
at
$0.415$
at
![]() $2R/H=0.7$
, and finally to
$2R/H=0.7$
, and finally to
![]() $0.46$
at
$0.46$
at
![]() $2R/H=0.8$
and
$2R/H=0.8$
and
![]() $0.85$
, as highlighted by the dashed lines. This suggests that the critical capillary number first decreases and then increases with the confinement ratio, and the minimum critical capillary number is achieved at a confinement ratio of around 0.5. These findings agree well with previous experimental and numerical studies (Janssen et al.
Reference Janssen, Vananroye, Van Puyvelde, Moldenaers and Anderson2010) in trend. Quantitatively speaking, the values of the critical capillary number obtained with the present method are a little higher than those obtained by Janssen et al. (Reference Janssen, Vananroye, Van Puyvelde, Moldenaers and Anderson2010) using the BIM; on the other hand, the present results are closer to the available experimental data in comparison with the numerical results of Janssen et al. (Reference Janssen, Vananroye, Van Puyvelde, Moldenaers and Anderson2010). In addition, it is clearly seen that a ternary breakup occurs instead of a binary breakup at higher confinement ratios, e.g.
$0.85$
, as highlighted by the dashed lines. This suggests that the critical capillary number first decreases and then increases with the confinement ratio, and the minimum critical capillary number is achieved at a confinement ratio of around 0.5. These findings agree well with previous experimental and numerical studies (Janssen et al.
Reference Janssen, Vananroye, Van Puyvelde, Moldenaers and Anderson2010) in trend. Quantitatively speaking, the values of the critical capillary number obtained with the present method are a little higher than those obtained by Janssen et al. (Reference Janssen, Vananroye, Van Puyvelde, Moldenaers and Anderson2010) using the BIM; on the other hand, the present results are closer to the available experimental data in comparison with the numerical results of Janssen et al. (Reference Janssen, Vananroye, Van Puyvelde, Moldenaers and Anderson2010). In addition, it is clearly seen that a ternary breakup occurs instead of a binary breakup at higher confinement ratios, e.g.
![]() $2R/H=0.8$
(also see figure 13), consistent with previous experimental and numerical findings (Janssen et al.
Reference Janssen, Vananroye, Van Puyvelde, Moldenaers and Anderson2010).
$2R/H=0.8$
(also see figure 13), consistent with previous experimental and numerical findings (Janssen et al.
Reference Janssen, Vananroye, Van Puyvelde, Moldenaers and Anderson2010).
Then, we investigate the breakup of a surfactant-laden droplet for various capillary numbers and confinement ratios at
![]() $x_{in}=0.3$
,
$x_{in}=0.3$
,
![]() $Re=0.1$
and
$Re=0.1$
and
![]() $Pe=10$
. The droplet and domain sizes are kept the same as those in the corresponding case of a clean droplet. Figure 12 shows the effect of the confinement ratio on the critical capillary number for droplet breakup in the surfactant-laden cases (represented by the dash-dotted lines). For low confinement ratios (
$Pe=10$
. The droplet and domain sizes are kept the same as those in the corresponding case of a clean droplet. Figure 12 shows the effect of the confinement ratio on the critical capillary number for droplet breakup in the surfactant-laden cases (represented by the dash-dotted lines). For low confinement ratios (
![]() $2R/H<0.7$
), the critical capillary number first decreases and then increases with increasing confinement ratio, and reaches its minimum value at a confinement ratio of around 0.5. Binary breakup always occurs at low confinement ratios, but ternary breakup is preferred at high confinement ratios. These findings are consistent with those in clean cases. Unlike in clean cases, however, the critical capillary number is almost independent of the confinement ratio for
$2R/H<0.7$
), the critical capillary number first decreases and then increases with increasing confinement ratio, and reaches its minimum value at a confinement ratio of around 0.5. Binary breakup always occurs at low confinement ratios, but ternary breakup is preferred at high confinement ratios. These findings are consistent with those in clean cases. Unlike in clean cases, however, the critical capillary number is almost independent of the confinement ratio for
![]() $2R/H\geqslant 0.7$
. It is worth noting that, to capture the exact variation of the critical capillary number with the confinement ratio, a large number of simulations are still required, which will be studied by exploiting massively parallel computing on graphics processing units (GPUs) in the near future. In addition, the presence of surfactants not only significantly decreases the critical capillary number for each confinement ratio but also may influence the mode of droplet breakup. For example, at a confinement ratio of 0.7, the breakup mode for a clean droplet is binary breakup, while ternary breakup occurs for a surfactant-laden droplet.
$2R/H\geqslant 0.7$
. It is worth noting that, to capture the exact variation of the critical capillary number with the confinement ratio, a large number of simulations are still required, which will be studied by exploiting massively parallel computing on graphics processing units (GPUs) in the near future. In addition, the presence of surfactants not only significantly decreases the critical capillary number for each confinement ratio but also may influence the mode of droplet breakup. For example, at a confinement ratio of 0.7, the breakup mode for a clean droplet is binary breakup, while ternary breakup occurs for a surfactant-laden droplet.
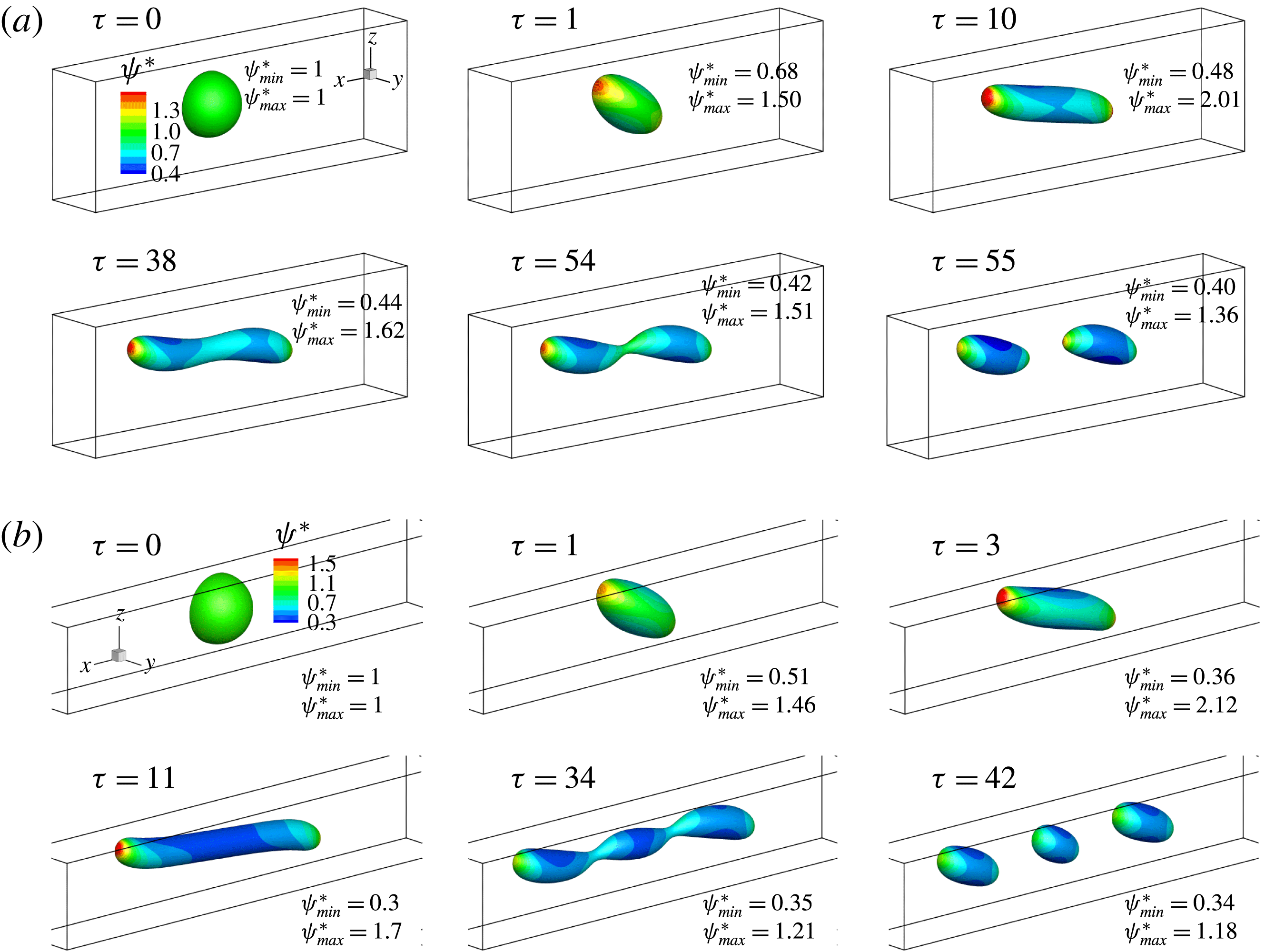
Figure 14. Snapshots of droplet shape at (a)
![]() $Ca=0.35$
,
$Ca=0.35$
,
![]() $2R/H=0.5$
and (b)
$2R/H=0.5$
and (b)
![]() $Ca=0.36$
,
$Ca=0.36$
,
![]() $2R/H=0.8$
for a surfactant-laden droplet. It should be noted that the droplet surface is coloured by the dimensionless surfactant concentration
$2R/H=0.8$
for a surfactant-laden droplet. It should be noted that the droplet surface is coloured by the dimensionless surfactant concentration
![]() $\unicode[STIX]{x1D713}^{\ast }$
.
$\unicode[STIX]{x1D713}^{\ast }$
.
To further understand the role of surfactants in droplet breakup, we plot snapshots of a surfactant-laden droplet for
![]() $2R/H=0.5$
and
$2R/H=0.5$
and
![]() $Ca=0.35$
in figure 14(a), where the droplet surface is coloured by the dimensionless surfactant concentration. In the stretching stage (see
$Ca=0.35$
in figure 14(a), where the droplet surface is coloured by the dimensionless surfactant concentration. In the stretching stage (see
![]() $\unicode[STIX]{x1D70F}=1$
and 10),
$\unicode[STIX]{x1D70F}=1$
and 10),
![]() $\unicode[STIX]{x1D713}_{max}^{\ast }$
increases but
$\unicode[STIX]{x1D713}_{max}^{\ast }$
increases but
![]() $\unicode[STIX]{x1D713}_{min}^{\ast }$
decreases, and the maximum surfactant concentration occurs near the droplet tips, leading to a more elongated droplet than the corresponding case of a clean droplet (see figure 13
a). After the initial stretching stage, a neck forms in the middle of the droplet and then gradually thins until the droplet finally breaks up into two equally sized daughter droplets. In the necking stage (see
$\unicode[STIX]{x1D713}_{min}^{\ast }$
decreases, and the maximum surfactant concentration occurs near the droplet tips, leading to a more elongated droplet than the corresponding case of a clean droplet (see figure 13
a). After the initial stretching stage, a neck forms in the middle of the droplet and then gradually thins until the droplet finally breaks up into two equally sized daughter droplets. In the necking stage (see
![]() $\unicode[STIX]{x1D70F}=38$
,
$\unicode[STIX]{x1D70F}=38$
,
![]() $54$
and
$54$
and
![]() $55$
),
$55$
),
![]() $\unicode[STIX]{x1D713}_{max}^{\ast }$
decreases and
$\unicode[STIX]{x1D713}_{max}^{\ast }$
decreases and
![]() $\unicode[STIX]{x1D713}_{min}^{\ast }$
almost remains constant, exhibiting a severe dilution of the surfactants, consistent with previous studies (Stone & Leal Reference Stone and Leal1990; Teigen et al.
Reference Teigen, Song, Lowengrub and Voigt2011). Moreover, it is interesting to note that in the stretching stage, the minimum surfactant concentration occurs in the middle of the droplet where the neck later forms, but as soon as the neck forms, the minimum surfactant concentration
$\unicode[STIX]{x1D713}_{min}^{\ast }$
almost remains constant, exhibiting a severe dilution of the surfactants, consistent with previous studies (Stone & Leal Reference Stone and Leal1990; Teigen et al.
Reference Teigen, Song, Lowengrub and Voigt2011). Moreover, it is interesting to note that in the stretching stage, the minimum surfactant concentration occurs in the middle of the droplet where the neck later forms, but as soon as the neck forms, the minimum surfactant concentration
![]() $\unicode[STIX]{x1D713}_{min}^{\ast }$
moves away from the necking region where the interface curvature is relatively high. As indicated in figure 12, a high confinement ratio favours ternary breakup in both clean and surfactant-laden cases. Figure 14(b) shows snapshots of ternary breakup for a surfactant-laden droplet at
$\unicode[STIX]{x1D713}_{min}^{\ast }$
moves away from the necking region where the interface curvature is relatively high. As indicated in figure 12, a high confinement ratio favours ternary breakup in both clean and surfactant-laden cases. Figure 14(b) shows snapshots of ternary breakup for a surfactant-laden droplet at
![]() $2R/H=0.8$
and
$2R/H=0.8$
and
![]() $Ca=0.36$
. Clearly, the droplet stretches to a more elongated shape before two necks form a little away from the droplet centre. During the stretching and necking stages,
$Ca=0.36$
. Clearly, the droplet stretches to a more elongated shape before two necks form a little away from the droplet centre. During the stretching and necking stages,
![]() $\unicode[STIX]{x1D713}_{max}^{\ast }$
and
$\unicode[STIX]{x1D713}_{max}^{\ast }$
and
![]() $\unicode[STIX]{x1D713}_{min}^{\ast }$
vary with the same trend as those at a confinement ratio of 0.5, but the dilution of surfactants in the necking stage is more severe as the droplet corresponds to a larger surface area. In the stretching stage, the minimum surfactant concentration still occurs in the middle of the droplet, but the necks do not form there; as soon as the necks form, the surfactant concentration in the necking region increases due to the increased interface curvature, which accelerates the necking process.
$\unicode[STIX]{x1D713}_{min}^{\ast }$
vary with the same trend as those at a confinement ratio of 0.5, but the dilution of surfactants in the necking stage is more severe as the droplet corresponds to a larger surface area. In the stretching stage, the minimum surfactant concentration still occurs in the middle of the droplet, but the necks do not form there; as soon as the necks form, the surfactant concentration in the necking region increases due to the increased interface curvature, which accelerates the necking process.
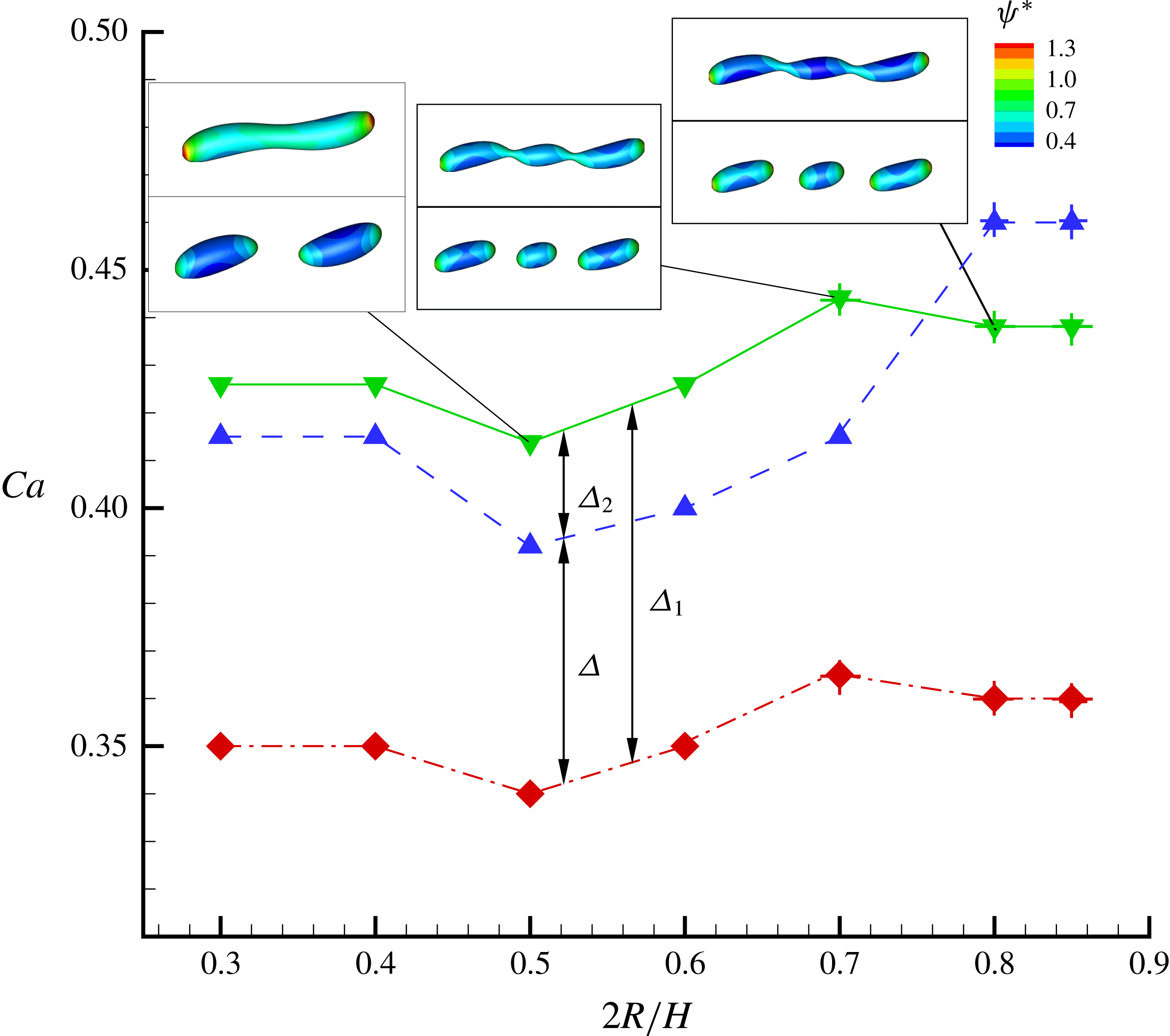
Figure 15. The critical capillary number of droplet breakup as a function of the confinement ratio for a clean droplet, a surfactant-laden droplet, and a surfactant-laden droplet with a reduced interfacial tension of
![]() $\unicode[STIX]{x1D70E}_{e}=\unicode[STIX]{x1D70E}_{0}/[1+E_{0}\ln (1-x_{in})]$
. Binary and ternary breakups are represented by discrete symbols without a ‘+’ and discrete symbols with a ‘+’ respectively. Here,
$\unicode[STIX]{x1D70E}_{e}=\unicode[STIX]{x1D70E}_{0}/[1+E_{0}\ln (1-x_{in})]$
. Binary and ternary breakups are represented by discrete symbols without a ‘+’ and discrete symbols with a ‘+’ respectively. Here,
![]() $\unicode[STIX]{x1D6E5}$
is the decrement of the critical capillary number due to the presence of surfactants, and
$\unicode[STIX]{x1D6E5}$
is the decrement of the critical capillary number due to the presence of surfactants, and
![]() $\unicode[STIX]{x1D6E5}_{1}$
and
$\unicode[STIX]{x1D6E5}_{1}$
and
![]() $\unicode[STIX]{x1D6E5}_{2}$
are its constituents. Each inset plots the droplet shapes before and after the breakup.
$\unicode[STIX]{x1D6E5}_{2}$
are its constituents. Each inset plots the droplet shapes before and after the breakup.
As mentioned above, the presence of surfactants decreases the critical capillary number of droplet breakup for each confinement ratio, and the decrease in the critical capillary number is also attributed to two mechanisms: (1) the reduction of the interfacial tension caused by the average surfactant concentration
![]() $\unicode[STIX]{x1D713}_{0}$
and (2) the non-uniform effects associated with non-uniform capillary pressure and Marangoni stresses. The contributions from these two mechanisms are denoted as
$\unicode[STIX]{x1D713}_{0}$
and (2) the non-uniform effects associated with non-uniform capillary pressure and Marangoni stresses. The contributions from these two mechanisms are denoted as
![]() $\unicode[STIX]{x1D6E5}_{1}$
and
$\unicode[STIX]{x1D6E5}_{1}$
and
![]() $\unicode[STIX]{x1D6E5}_{2}$
, which are shown in figure 15. It should be noted in this figure that the dashed and dash-dotted lines are directly taken from figure 12, and the solid lines with inverted triangles are obtained by ruling out the reduction of the interfacial tension caused by
$\unicode[STIX]{x1D6E5}_{2}$
, which are shown in figure 15. It should be noted in this figure that the dashed and dash-dotted lines are directly taken from figure 12, and the solid lines with inverted triangles are obtained by ruling out the reduction of the interfacial tension caused by
![]() $\unicode[STIX]{x1D713}_{0}$
in the surfactant-laden cases. For each of the confinement ratios considered,
$\unicode[STIX]{x1D713}_{0}$
in the surfactant-laden cases. For each of the confinement ratios considered,
![]() $\unicode[STIX]{x1D6E5}_{1}$
always has a positive contribution to the decrease in the critical capillary number. Moreover, we surprisingly find that the non-uniform effects (
$\unicode[STIX]{x1D6E5}_{1}$
always has a positive contribution to the decrease in the critical capillary number. Moreover, we surprisingly find that the non-uniform effects (
![]() $\unicode[STIX]{x1D6E5}_{2}$
) increase
$\unicode[STIX]{x1D6E5}_{2}$
) increase
![]() $Ca_{cr}$
, thus retarding the droplet breakup, for low confinement ratios where binary breakup occurs, but decrease
$Ca_{cr}$
, thus retarding the droplet breakup, for low confinement ratios where binary breakup occurs, but decrease
![]() $Ca_{cr}$
, thus promoting the droplet breakup, for high confinement ratios where ternary breakup occurs. The difference at low and high confinement ratios is probably explained as follows. For low confinement ratios, it can be observed from, e.g., figure 14(a) that in the entire stretching stage, the minimum value of surfactant concentration is located in the middle of the droplet, where the interfacial tension is higher than the average value. Since the interfacial tension acts to stabilize the interface, the surfactants retard the droplet deformation in the middle region, thus against the formation of a neck. On the other hand, for high confinement ratios, it is noticed from, e.g., figure 14(b) that the necks are formed in the regions away from the droplet centre, where the surfactant concentration is relatively high. The resulting low interfacial tension favours the formation of necks, thus promoting the droplet breakup.
$Ca_{cr}$
, thus promoting the droplet breakup, for high confinement ratios where ternary breakup occurs. The difference at low and high confinement ratios is probably explained as follows. For low confinement ratios, it can be observed from, e.g., figure 14(a) that in the entire stretching stage, the minimum value of surfactant concentration is located in the middle of the droplet, where the interfacial tension is higher than the average value. Since the interfacial tension acts to stabilize the interface, the surfactants retard the droplet deformation in the middle region, thus against the formation of a neck. On the other hand, for high confinement ratios, it is noticed from, e.g., figure 14(b) that the necks are formed in the regions away from the droplet centre, where the surfactant concentration is relatively high. The resulting low interfacial tension favours the formation of necks, thus promoting the droplet breakup.
4.2.2 Influence of the Reynolds number
Another important parameter governing droplet breakup is the Reynolds number, and its influence on the critical capillary number is investigated for both clean and surfactant-laden droplets at a confinement ratio of 0.5. The Reynolds number is varied from 0.05 to 10. For surfactant-laden droplets, the surfactant coverage and Péclet number are still taken as
![]() $x_{in}=0.3$
and
$x_{in}=0.3$
and
![]() $Pe=10$
.
$Pe=10$
.
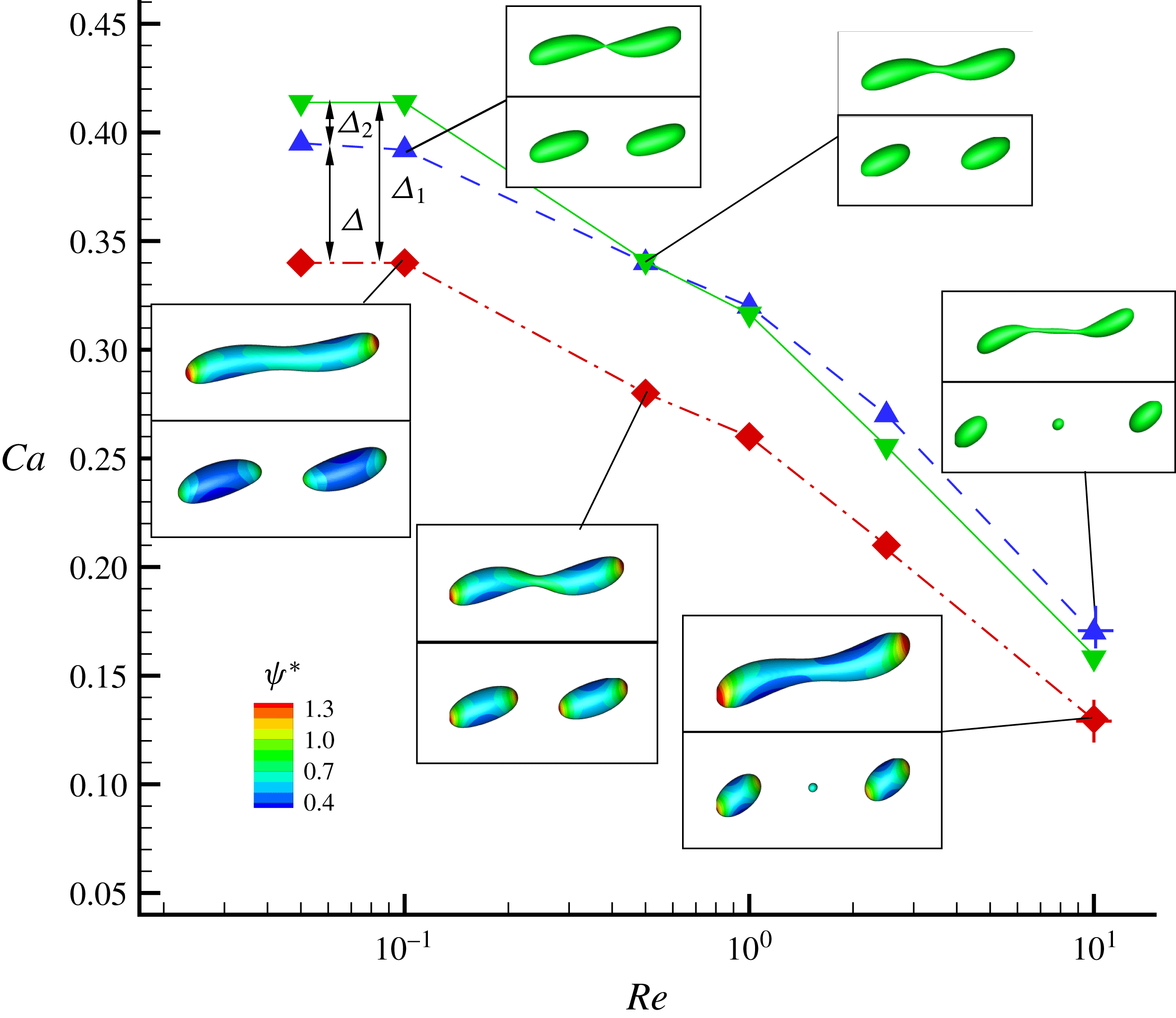
Figure 16. The critical capillary number of droplet breakup as a function of the Reynolds number at a confinement ratio of 0.5 for clean droplets (dashed lines with triangles), surfactant-laden droplets (dash-dotted lines with diamonds), and surfactant-laden droplets with a reduced interfacial tension of
![]() $\unicode[STIX]{x1D70E}_{e}$
(solid lines with inverted triangles). Binary and ternary breakups are represented by discrete symbols without a ‘+’ and discrete symbols with a ‘+’ respectively. Here,
$\unicode[STIX]{x1D70E}_{e}$
(solid lines with inverted triangles). Binary and ternary breakups are represented by discrete symbols without a ‘+’ and discrete symbols with a ‘+’ respectively. Here,
![]() $\unicode[STIX]{x1D6E5}$
is the decrement of the critical capillary number due to the presence of surfactants, and
$\unicode[STIX]{x1D6E5}$
is the decrement of the critical capillary number due to the presence of surfactants, and
![]() $\unicode[STIX]{x1D6E5}_{1}$
and
$\unicode[STIX]{x1D6E5}_{1}$
and
![]() $\unicode[STIX]{x1D6E5}_{2}$
are its constituents. Each inset plots the droplet shapes before and after the breakup.
$\unicode[STIX]{x1D6E5}_{2}$
are its constituents. Each inset plots the droplet shapes before and after the breakup.
Figure 16 displays the simulation results of our method for clean and surfactant-laden droplets. Again, the critical capillary number is defined as the lowest capillary number found at which an initially spherical droplet breaks up. As the Reynolds number increases, the critical capillary number first remains almost unchanged until
![]() $Re=0.1$
and then decreases monotonically for the clean droplets, which is consistent with previous findings in a surfactant-free system (Renardy & Cristini Reference Renardy and Cristini2001). For the surfactant-laden droplets, the critical capillary number varies with
$Re=0.1$
and then decreases monotonically for the clean droplets, which is consistent with previous findings in a surfactant-free system (Renardy & Cristini Reference Renardy and Cristini2001). For the surfactant-laden droplets, the critical capillary number varies with
![]() $Re$
with the same trend as for the clean droplets. In either clean or surfactant-laden cases, binary breakup occurs for
$Re$
with the same trend as for the clean droplets. In either clean or surfactant-laden cases, binary breakup occurs for
![]() $Re\leqslant 2.5$
, whereas for
$Re\leqslant 2.5$
, whereas for
![]() $Re=10$
, ternary breakup occurs, and among the formed droplets, the middle one is very small. In addition, the presence of surfactants can decrease the value of
$Re=10$
, ternary breakup occurs, and among the formed droplets, the middle one is very small. In addition, the presence of surfactants can decrease the value of
![]() $Ca_{cr}$
for each
$Ca_{cr}$
for each
![]() $Re$
, but the influence of surfactants on
$Re$
, but the influence of surfactants on
![]() $Ca_{cr}$
is smaller in ternary breakup than in binary breakup. This is because in ternary breakup, the dominant convection sweeps more surfactants to both tips of the droplet, which leads to a lower surfactant concentration in the middle part of the droplet, thereby weakening the effect of surfactants on the breakup.
$Ca_{cr}$
is smaller in ternary breakup than in binary breakup. This is because in ternary breakup, the dominant convection sweeps more surfactants to both tips of the droplet, which leads to a lower surfactant concentration in the middle part of the droplet, thereby weakening the effect of surfactants on the breakup.
Figure 16 also plots
![]() $Ca_{cr}$
as a function of
$Ca_{cr}$
as a function of
![]() $Re$
for a surfactant-laden droplet with a reduced interfacial tension of
$Re$
for a surfactant-laden droplet with a reduced interfacial tension of
![]() $\unicode[STIX]{x1D70E}_{e}$
(represented by the solid lines with inverted triangles). For each
$\unicode[STIX]{x1D70E}_{e}$
(represented by the solid lines with inverted triangles). For each
![]() $Re$
,
$Re$
,
![]() $\unicode[STIX]{x1D6E5}_{1}$
, which accounts for the reduction of the interfacial tension by
$\unicode[STIX]{x1D6E5}_{1}$
, which accounts for the reduction of the interfacial tension by
![]() $\unicode[STIX]{x1D713}_{0}$
, always has a positive contribution to the decrease of
$\unicode[STIX]{x1D713}_{0}$
, always has a positive contribution to the decrease of
![]() $Ca_{cr}$
, consistent with the previous observation in figure 15. Depending on
$Ca_{cr}$
, consistent with the previous observation in figure 15. Depending on
![]() $Re$
, the non-uniform effects
$Re$
, the non-uniform effects
![]() $\unicode[STIX]{x1D6E5}_{2}$
play different roles in influencing the droplet breakup. Specifically, the non-uniform effects prevent droplet breakup for low
$\unicode[STIX]{x1D6E5}_{2}$
play different roles in influencing the droplet breakup. Specifically, the non-uniform effects prevent droplet breakup for low
![]() $Re$
, but promote breakup for high
$Re$
, but promote breakup for high
![]() $Re$
. Moreover, we notice that the non-uniform effects on the droplet breakup are overall smaller at high
$Re$
. Moreover, we notice that the non-uniform effects on the droplet breakup are overall smaller at high
![]() $Re$
than at low
$Re$
than at low
![]() $Re$
, which is attributed to the enhanced surfactant dilution at high
$Re$
, which is attributed to the enhanced surfactant dilution at high
![]() $Re$
.
$Re$
.
5 Collision of two droplets in a simple shear flow
One of the important functions of surfactant in microfluidic applications is to inhibit the coalescence of droplets (Link et al. Reference Link, Anna, Weitz and Stone2004; Baret Reference Baret2012; Krebs, Schroën & Boom Reference Krebs, Schroën and Boom2012). To demonstrate the capability of the hybrid method in dealing with interface merging and to explore how a non-uniform distribution of surfactants affects droplet coalescence, we consider the collision of two equal-sized droplets subject to a simple shear flow in both surfactant-free and surfactant-contaminated systems (see figure 17).
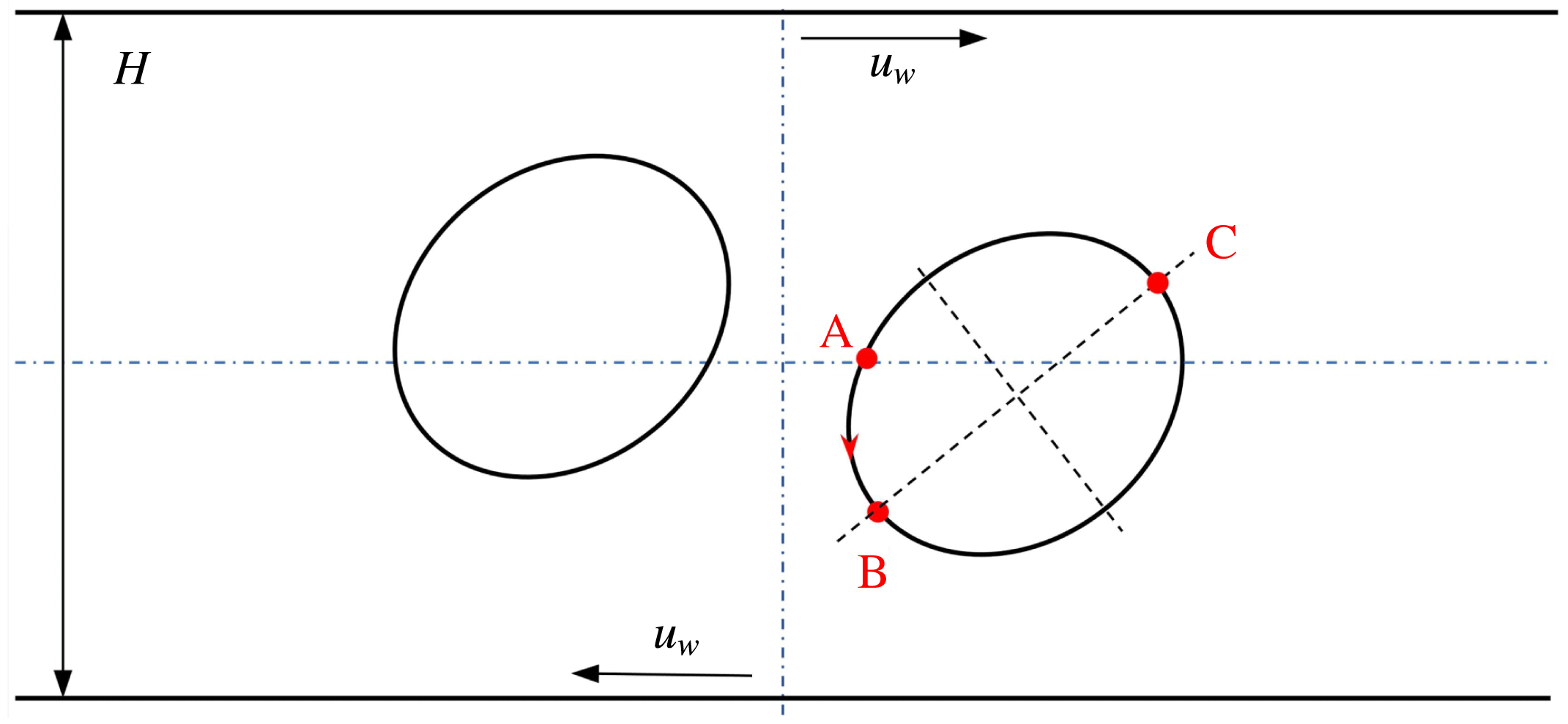
Figure 17. Illustration of the collision of two droplets in a 2D shear flow. It should be noted that the point ‘A’ is the left intersection point of the right droplet and the horizontal centre line, and the points ‘B’ and ‘C’ are the near tip and the far tip of the right droplet.
The computational domain is taken as
![]() $720\times 480$
, and two circular droplets with equal radius
$720\times 480$
, and two circular droplets with equal radius
![]() $R=80$
are initially placed at (200, 280) and (540, 200). In the surfactant-contaminated system, a surfactant coverage of
$R=80$
are initially placed at (200, 280) and (540, 200). In the surfactant-contaminated system, a surfactant coverage of
![]() $x_{in}=0.3$
is considered. Other dimensionless parameters are selected as
$x_{in}=0.3$
is considered. Other dimensionless parameters are selected as
![]() $Re=0.4$
,
$Re=0.4$
,
![]() $E_{0}=0.4$
and
$E_{0}=0.4$
and
![]() $Pe=10$
. It is known that a reduction of the interfacial tension, and thus an increase of the effective capillary number, due to the presence of surfactants can inhibit droplet coalescence (Shardt, Derksen & Mitra Reference Shardt, Derksen and Mitra2013). To rule out the effect of average surfactant concentration in reducing the interfacial tension, the effective capillary number
$Pe=10$
. It is known that a reduction of the interfacial tension, and thus an increase of the effective capillary number, due to the presence of surfactants can inhibit droplet coalescence (Shardt, Derksen & Mitra Reference Shardt, Derksen and Mitra2013). To rule out the effect of average surfactant concentration in reducing the interfacial tension, the effective capillary number
is used in both the surfactant-free and surfactant-contaminated systems.
Figure 18. Collision of two droplets in simple shear flow for clean (the dashed lines) and surfactant-laden cases at
![]() $Re=0.4$
and
$Re=0.4$
and
![]() $Ca_{e}=0.1$
. In the surfactant-laden case,
$Ca_{e}=0.1$
. In the surfactant-laden case,
![]() $Pe=10$
,
$Pe=10$
,
![]() $x_{in}=0.3$
and
$x_{in}=0.3$
and
![]() $E_{0}=0.4$
, and the interface is coloured by the dimensionless surfactant concentration
$E_{0}=0.4$
, and the interface is coloured by the dimensionless surfactant concentration
![]() $\unicode[STIX]{x1D713}^{\ast }$
.
$\unicode[STIX]{x1D713}^{\ast }$
.
Figure 18 shows the evolution of the droplet shape for the clean droplets and surfactant-contaminated droplets at times (
![]() $\unicode[STIX]{x1D70F}=\dot{\unicode[STIX]{x1D6FE}}t$
) of 0, 2.3, 4.6, 5.6, 6.4 and 8.1. In this figure, we plot the contour of
$\unicode[STIX]{x1D70F}=\dot{\unicode[STIX]{x1D6FE}}t$
) of 0, 2.3, 4.6, 5.6, 6.4 and 8.1. In this figure, we plot the contour of
![]() $\unicode[STIX]{x1D70C}^{N}=0$
for the clean droplets and the surfactant concentration distributions for the surfactant-contaminated droplets. It is seen that the clean droplets first move towards each other (figure 18
a,b), then the film between the droplets becomes very thin (figure 18
c), and finally the two droplets merge together as a result of the interfacial tension (figure 18
d–f). On the contrary, for surfactant-contaminated droplets, the thin film between the droplets maintains a certain thickness, and the droplets slide over each other without coalescence. This clearly shows that the non-uniform effects from non-uniform capillary pressure and Marangoni stresses act as an additional repulsive force to prevent droplet coalescence, which is consistent with previous experimental and numerical findings (Hu, Pine & Leal Reference Hu, Pine and Leal2000; Dai & Leal Reference Dai and Leal2008; Liu & Zhang Reference Liu and Zhang2010).
$\unicode[STIX]{x1D70C}^{N}=0$
for the clean droplets and the surfactant concentration distributions for the surfactant-contaminated droplets. It is seen that the clean droplets first move towards each other (figure 18
a,b), then the film between the droplets becomes very thin (figure 18
c), and finally the two droplets merge together as a result of the interfacial tension (figure 18
d–f). On the contrary, for surfactant-contaminated droplets, the thin film between the droplets maintains a certain thickness, and the droplets slide over each other without coalescence. This clearly shows that the non-uniform effects from non-uniform capillary pressure and Marangoni stresses act as an additional repulsive force to prevent droplet coalescence, which is consistent with previous experimental and numerical findings (Hu, Pine & Leal Reference Hu, Pine and Leal2000; Dai & Leal Reference Dai and Leal2008; Liu & Zhang Reference Liu and Zhang2010).
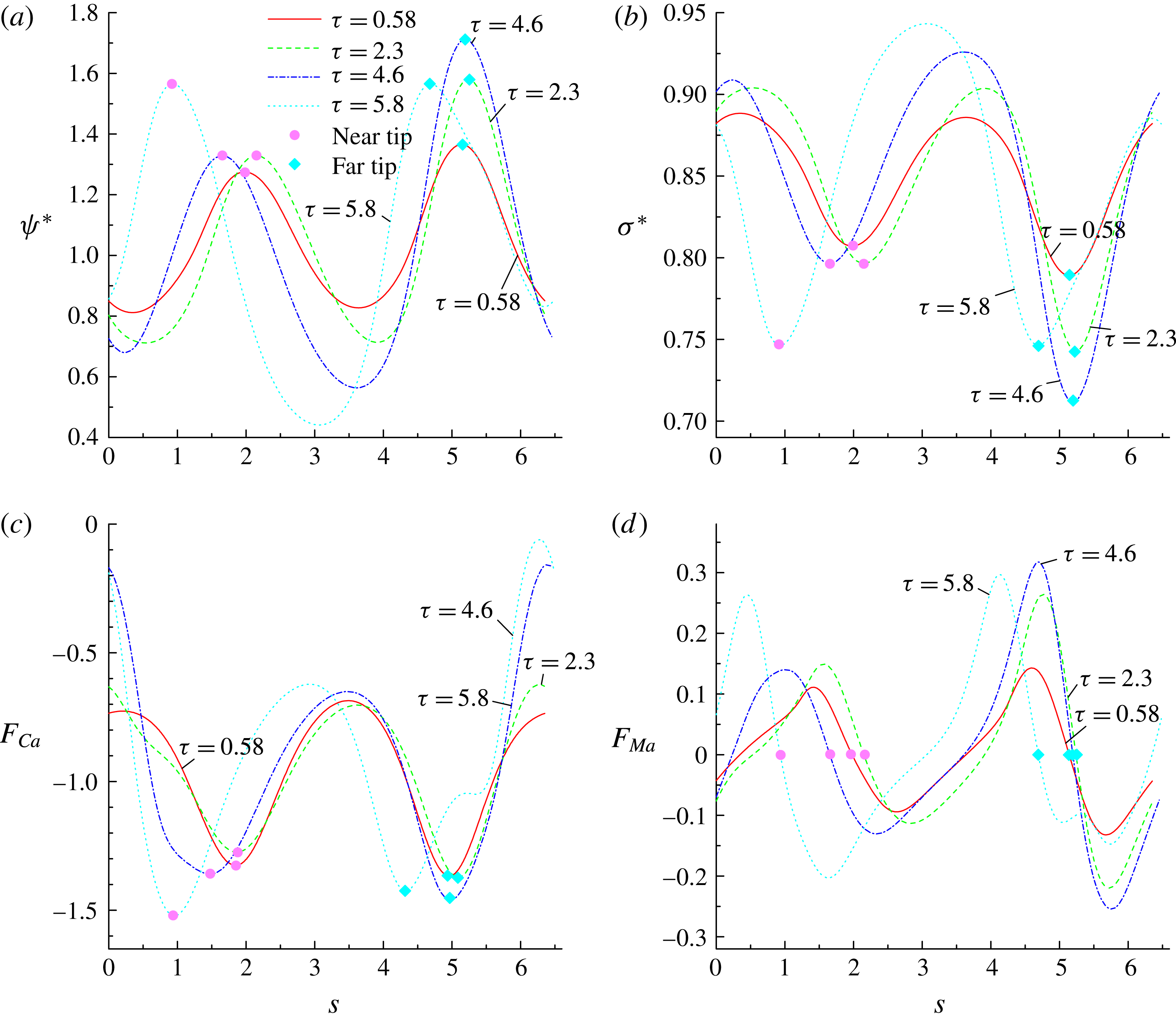
Figure 19. The distributions of (a) the dimensionless surfactant concentration
![]() $\unicode[STIX]{x1D713}^{\ast }$
, (b) the dimensionless interfacial tension
$\unicode[STIX]{x1D713}^{\ast }$
, (b) the dimensionless interfacial tension
![]() $\unicode[STIX]{x1D70E}^{\ast }$
, (c) the signed dimensionless capillary force
$\unicode[STIX]{x1D70E}^{\ast }$
, (c) the signed dimensionless capillary force
![]() $F_{Ca}$
and (d) the signed dimensionless Marangoni force
$F_{Ca}$
and (d) the signed dimensionless Marangoni force
![]() $F_{Ma}$
along the arclength
$F_{Ma}$
along the arclength
![]() $s$
for
$s$
for
![]() $Re=0.4$
,
$Re=0.4$
,
![]() $Pe=10$
,
$Pe=10$
,
![]() $Ca_{e}=0.1$
,
$Ca_{e}=0.1$
,
![]() $E_{0}=0.4$
,
$E_{0}=0.4$
,
![]() $x_{in}=0.3$
at dimensionless times of
$x_{in}=0.3$
at dimensionless times of
![]() $\unicode[STIX]{x1D70F}=0.58$
, 2.3, 4.6 and 5.8. It should be noted that the near tip represents the one first encountered as
$\unicode[STIX]{x1D70F}=0.58$
, 2.3, 4.6 and 5.8. It should be noted that the near tip represents the one first encountered as
![]() $s$
increases.
$s$
increases.
As shown in figure 18, for the surfactant-contaminated droplets, surfactants are swept towards droplet tips at the beginning, but the maximum values of the surfactant concentration at the two tips are unequal due to the asymmetry of the shear flow with respect to the droplet centre and the effect from the neighbouring droplet. As the two droplets move close to each other, the symmetry of the surfactant concentration distribution is further broken, and we can observe that the surfactant concentration is greatly enhanced at the near tip (point ‘B’ in figure 17), but remains almost unchanged at the far tip (point ‘C’ in figure 17). The variation of the surfactant concentration can be observed more clearly in figure 19, which plots the distributions of the dimensionless surfactant concentration
![]() $\unicode[STIX]{x1D713}^{\ast }$
, the dimensionless interfacial tension
$\unicode[STIX]{x1D713}^{\ast }$
, the dimensionless interfacial tension
![]() $\unicode[STIX]{x1D70E}^{\ast }$
, and the signed magnitudes of the dimensionless capillary force
$\unicode[STIX]{x1D70E}^{\ast }$
, and the signed magnitudes of the dimensionless capillary force
![]() $F_{Ca}$
and Marangoni force
$F_{Ca}$
and Marangoni force
![]() $F_{Ma}$
along the arclength
$F_{Ma}$
along the arclength
![]() $s$
at times of
$s$
at times of
![]() $\unicode[STIX]{x1D70F}=0.58$
, 2.3, 4.6 and 5.8. Here,
$\unicode[STIX]{x1D70F}=0.58$
, 2.3, 4.6 and 5.8. Here,
![]() $s$
is measured from the left intersection point (point ‘A’ in figure 17) between the droplet interface and the horizontal centreline, and increases anticlockwise along the interface. As shown in figure 19(a), four stages can be identified in the evolution of the surfactant concentration: (1) in the early stage, e.g.
$s$
is measured from the left intersection point (point ‘A’ in figure 17) between the droplet interface and the horizontal centreline, and increases anticlockwise along the interface. As shown in figure 19(a), four stages can be identified in the evolution of the surfactant concentration: (1) in the early stage, e.g.
![]() $\unicode[STIX]{x1D70F}=0.58$
, the surfactants predominantly accumulate at the droplet tips due to the outer shear flow, producing nearly equal maximum surfactant concentration; (2) as
$\unicode[STIX]{x1D70F}=0.58$
, the surfactants predominantly accumulate at the droplet tips due to the outer shear flow, producing nearly equal maximum surfactant concentration; (2) as
![]() $\unicode[STIX]{x1D70F}$
increases from 0.58 to 4.6,
$\unicode[STIX]{x1D70F}$
increases from 0.58 to 4.6,
![]() $\unicode[STIX]{x1D713}^{\ast }$
at the far tip almost holds a constant value while
$\unicode[STIX]{x1D713}^{\ast }$
at the far tip almost holds a constant value while
![]() $\unicode[STIX]{x1D713}^{\ast }$
at the near tip increases; (3) when the gap between the two droplets decreases to a minimum value at
$\unicode[STIX]{x1D713}^{\ast }$
at the near tip increases; (3) when the gap between the two droplets decreases to a minimum value at
![]() $\unicode[STIX]{x1D70F}\simeq 4.6$
, the maximum
$\unicode[STIX]{x1D70F}\simeq 4.6$
, the maximum
![]() $\unicode[STIX]{x1D713}^{\ast }$
is achieved at the far tip; and (4) as the droplets slide over each other (see, e.g.,
$\unicode[STIX]{x1D713}^{\ast }$
is achieved at the far tip; and (4) as the droplets slide over each other (see, e.g.,
![]() $\unicode[STIX]{x1D70F}=5.8$
),
$\unicode[STIX]{x1D70F}=5.8$
),
![]() $\unicode[STIX]{x1D713}^{\ast }$
at the far tip decreases, but
$\unicode[STIX]{x1D713}^{\ast }$
at the far tip decreases, but
![]() $\unicode[STIX]{x1D713}^{\ast }$
at the near tip increases.
$\unicode[STIX]{x1D713}^{\ast }$
at the near tip increases.
Figure 20. The velocity vectors and the streamlines in the vicinity of the gap at
![]() $\unicode[STIX]{x1D70F}=4.6$
for
$\unicode[STIX]{x1D70F}=4.6$
for
![]() $Re=0.4$
,
$Re=0.4$
,
![]() $Pe=10$
,
$Pe=10$
,
![]() $x_{in}=0.3$
,
$x_{in}=0.3$
,
![]() $E_{0}=0.4$
and
$E_{0}=0.4$
and
![]() $Ca_{e}=0.1$
: (a) clean droplets; (b) surfactant-laden droplets.
$Ca_{e}=0.1$
: (a) clean droplets; (b) surfactant-laden droplets.
The distribution of
![]() $\unicode[STIX]{x1D713}^{\ast }$
determines the interfacial tension, thus influencing the outcome of the droplet collision. From figure 19(b), we see that the dimensionless interfacial tension
$\unicode[STIX]{x1D713}^{\ast }$
determines the interfacial tension, thus influencing the outcome of the droplet collision. From figure 19(b), we see that the dimensionless interfacial tension
![]() $\unicode[STIX]{x1D70E}^{\ast }$
is distributed unevenly on the droplet interface, and its non-uniformity increases as the droplets come close to each other, which leads to increased non-uniform effects associated with non-uniform capillary forces and Marangoni stresses (see figure 19
d). The non-uniform capillary forces and Marangoni stresses are able to reduce the interface mobility during the droplet–droplet interaction (an indicator is the broader gap between the droplets in the presence of surfactants, which can be seen from the comparison between figures 20
a and 20
b), thus hindering the coalescence of droplets. Interestingly, we find that at
$\unicode[STIX]{x1D70E}^{\ast }$
is distributed unevenly on the droplet interface, and its non-uniformity increases as the droplets come close to each other, which leads to increased non-uniform effects associated with non-uniform capillary forces and Marangoni stresses (see figure 19
d). The non-uniform capillary forces and Marangoni stresses are able to reduce the interface mobility during the droplet–droplet interaction (an indicator is the broader gap between the droplets in the presence of surfactants, which can be seen from the comparison between figures 20
a and 20
b), thus hindering the coalescence of droplets. Interestingly, we find that at
![]() $s=0$
, as the droplets approach each other,
$s=0$
, as the droplets approach each other,
![]() $\unicode[STIX]{x1D713}^{\ast }$
does not change much, but
$\unicode[STIX]{x1D713}^{\ast }$
does not change much, but
![]() $F_{Ca}$
increases drastically, which is attributed to the increase in the local interface curvature. In figure 19(d), it is clearly shown that
$F_{Ca}$
increases drastically, which is attributed to the increase in the local interface curvature. In figure 19(d), it is clearly shown that
![]() $F_{Ma}$
is fixed at 0 at both tips, and the maximum or minimum values of
$F_{Ma}$
is fixed at 0 at both tips, and the maximum or minimum values of
![]() $F_{Ma}$
always occur at locations near the far tip. Finally, it is worth noting that the addition of surfactants can lead to considerable variation of the velocity vectors and the streamlines in the vicinity of the gap, which can be seen from figure 20. For clean droplets, a single vortex is formed with its centre in the gap, whereas for surfactant-contaminated droplets, a counter-rotating vortex pair is observed, with each vortex centred near the gap inside its corresponding droplet.
$F_{Ma}$
always occur at locations near the far tip. Finally, it is worth noting that the addition of surfactants can lead to considerable variation of the velocity vectors and the streamlines in the vicinity of the gap, which can be seen from figure 20. For clean droplets, a single vortex is formed with its centre in the gap, whereas for surfactant-contaminated droplets, a counter-rotating vortex pair is observed, with each vortex centred near the gap inside its corresponding droplet.
6 Conclusions
In summary, a hybrid LB–FD method has been proposed to simulate interfacial flows with insoluble surfactants. The hybrid method solves the immiscible two-phase flows by using the LB colour-gradient model, in which the Marangoni stress is incorporated into the perturbation term to account for the tangential stress created by the non-uniform interfacial tension, and describes the transport of surfactant concentration through a convection–diffusion equation of diffuse-interface form, which is solved in the entire fluid domain by the FD method. The LB and FD methods are coupled by an EOS that relates the interfacial tension to the surfactant concentration and can be selected arbitrarily. The accuracy of the hybrid method has been validated for the deformation of a surfactant-laden droplet in an 3D extensional flow and a 2D shear flow.
The hybrid method has been used to study the effect of surfactants on droplet deformation and breakup in a three-dimensional shear flow. It has been found that the presence of surfactants increases droplet deformation due to (1) a reduction of the interfacial tension caused by the average surfactant concentration and (2) the non-uniform effects from non-uniform capillary pressure and Marangoni stresses. The former accounts for most of the effect of the surfactants on the droplet deformation. Increase of the surface Péclet number can increase the non-uniformity of the surfactant distribution, thus leading to enhanced droplet deformation. Regarding the droplet breakup, we have focused on the critical capillary number (
![]() $Ca_{cr}$
) of droplet breakup for various confinement ratios (
$Ca_{cr}$
) of droplet breakup for various confinement ratios (
![]() $2R/H$
) and Reynolds numbers. For clean droplets,
$2R/H$
) and Reynolds numbers. For clean droplets,
![]() $Ca_{cr}$
first increases and then decreases with the confinement ratio, and the minimum
$Ca_{cr}$
first increases and then decreases with the confinement ratio, and the minimum
![]() $Ca_{cr}$
is achieved at a confinement ratio of around 0.5. For surfactant-laden droplets,
$Ca_{cr}$
is achieved at a confinement ratio of around 0.5. For surfactant-laden droplets,
![]() $Ca_{cr}$
varies with the confinement ratio with the same trend as for clean droplets for
$Ca_{cr}$
varies with the confinement ratio with the same trend as for clean droplets for
![]() $2R/H<0.7$
, but for higher confinement ratios,
$2R/H<0.7$
, but for higher confinement ratios,
![]() $Ca_{cr}$
remains almost constant. The presence of surfactants decreases
$Ca_{cr}$
remains almost constant. The presence of surfactants decreases
![]() $Ca_{cr}$
for each confinement ratio, and the decrease in
$Ca_{cr}$
for each confinement ratio, and the decrease in
![]() $Ca_{cr}$
is also attributed to the reduction in average interfacial tension and the non-uniform effects. It has been identified that the non-uniform effects prevent droplet breakup at low confinement ratios where binary breakup occurs, but promote breakup at high confinement ratios where ternary breakup occurs. In either clean or surfactant-laden cases,
$Ca_{cr}$
is also attributed to the reduction in average interfacial tension and the non-uniform effects. It has been identified that the non-uniform effects prevent droplet breakup at low confinement ratios where binary breakup occurs, but promote breakup at high confinement ratios where ternary breakup occurs. In either clean or surfactant-laden cases,
![]() $Ca_{cr}$
first remains almost unchanged until
$Ca_{cr}$
first remains almost unchanged until
![]() $Re=0.1$
, and then decreases monotonically with increasing Reynolds number. The mode of droplet breakup depends on the confinement ratio and Reynolds number: a higher confinement ratio or Reynolds number favours ternary breakup.
$Re=0.1$
, and then decreases monotonically with increasing Reynolds number. The mode of droplet breakup depends on the confinement ratio and Reynolds number: a higher confinement ratio or Reynolds number favours ternary breakup.
We have also simulated the collision of two equal-sized droplets subject to a simple shear flow in both surfactant-free and surfactant-contaminated systems with equal effective capillary numbers. It is observed that the non-uniform effects associated with non-uniform capillary forces and Marangoni stresses can immobilize the interfaces during the droplet–droplet approach, thus acting as a repulsive force to prevent droplet coalescence.
The present study not only provides a simple, accurate and reliable numerical method for the simulation of interfacial flows with insoluble surfactants, but also improves our understanding of droplet dynamics in confined shear flows with the presence of surfactants.
Acknowledgements
This work is financially supported by the National Natural Science Foundation of China (no. 51506168 and 51711530130), the National Key Research and Development Program of China (no. 2016YFB0200902), the China Postdoctoral Science Foundation (no. 2016M590943), and the Thousand Youth Talents Program for Distinguished Young Scholars. This work is also supported by the UK’s Engineering and Physical Sciences Research Council (EPSRC) under grant EP/L00030X/1.