Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Camporeale, Carlo
and
Ridolfi, Luca
2012.
Hydrodynamic-Driven Stability Analysis of Morphological Patterns on Stalactites and Implications for Cave Paleoflow Reconstructions.
Physical Review Letters,
Vol. 108,
Issue. 23,
Solari, Luca
and
Parker, Gary
2013.
Morphodynamic modeling of the basal boundary of ice cover on brackish lakes.
Journal of Geophysical Research: Earth Surface,
Vol. 118,
Issue. 3,
p.
1432.
Camporeale, C.
Mantelli, E.
and
Manes, C.
2013.
Interplay among unstable modes in films over permeable walls.
Journal of Fluid Mechanics,
Vol. 719,
Issue. ,
p.
527.
Gheorghiu, Călin-Ioan
2014.
Spectral Methods for Non-Standard Eigenvalue Problems.
p.
19.
Camporeale, Carlo
and
Schmid, Peter J.
2015.
Parametric resonance in unsteady watertable flow.
Journal of Fluid Mechanics,
Vol. 768,
Issue. ,
p.
524.
NAITO, Kensuke
IZUMI, Norihiro
YOKOKAWA, Miwa
and
SUMITA, Takashi
2015.
BOUNDARY WAVES FORMED ON ICE BY TURBULENT FLOW.
Journal of Japan Society of Civil Engineers, Ser. B1 (Hydraulic Engineering),
Vol. 71,
Issue. 4,
p.
I_1027.
Vesipa, R.
Camporeale, C.
and
Ridolfi, L.
2015.
Thin-film-induced morphological instabilities over calcite surfaces.
Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 471,
Issue. 2176,
p.
20150031.
Mantelli, E.
Camporeale, C.
and
Ridolfi, L.
2015.
Supraglacial channel inception: Modeling and processes.
Water Resources Research,
Vol. 51,
Issue. 9,
p.
7044.
Camporeale, C.
2015.
Hydrodynamically locked morphogenesis in karst and ice flutings.
Journal of Fluid Mechanics,
Vol. 778,
Issue. ,
p.
89.
YOKOKAWA, Miwa
2016.
Cyclic Steps on Ice:.
Journal of Geography (Chigaku Zasshi),
Vol. 125,
Issue. 1,
p.
91.
Yokokawa, M.
Izumi, N.
Naito, K.
Parker, G.
Yamada, T.
and
Greve, R.
2016.
Cyclic steps on ice.
Journal of Geophysical Research: Earth Surface,
Vol. 121,
Issue. 5,
p.
1023.
ST. Germain, S. L.
and
Moorman, B. J.
2016.
The development of a pulsating supraglacial stream.
Annals of Glaciology,
Vol. 57,
Issue. 72,
p.
31.
IZUMI, Norihiro
2016.
Morphodynamics on the Ice Floor.
Journal of Geography (Chigaku Zasshi),
Vol. 125,
Issue. 1,
p.
105.
Bertagni, Matteo Bernard
and
Camporeale, Carlo
2017.
Nonlinear and subharmonic stability analysis in film-driven morphological patterns.
Physical Review E,
Vol. 96,
Issue. 5,
Camporeale, Carlo
2017.
An asymptotic approach to the crenulation instability.
Journal of Fluid Mechanics,
Vol. 826,
Issue. ,
p.
636.
Camporeale, Carlo
Vesipa, Riccardo
and
Ridolfi, Luca
2017.
Convective-absolute nature of ripple instabilities on ice and icicles.
Physical Review Fluids,
Vol. 2,
Issue. 5,
Claudin, Philippe
Durán, Orencio
and
Andreotti, Bruno
2017.
Dissolution instability and roughening transition.
Journal of Fluid Mechanics,
Vol. 832,
Issue. ,
Bushuk, Mitchell
Holland, David M.
Stanton, Timothy P.
Stern, Alon
and
Gray, Callum
2019.
Ice scallops: a laboratory investigation of the ice–water interface.
Journal of Fluid Mechanics,
Vol. 873,
Issue. ,
p.
942.
Toppaladoddi, S.
and
Wettlaufer, J. S.
2019.
The combined effects of shear and buoyancy on phase boundary stability.
Journal of Fluid Mechanics,
Vol. 868,
Issue. ,
p.
648.
Bordiec, M.
Carpy, S.
Bourgeois, O.
Herny, C.
Massé, M.
Perret, L.
Claudin, P.
Pochat, S.
and
Douté, S.
2020.
Sublimation waves: Geomorphic markers of interactions between icy planetary surfaces and winds.
Earth-Science Reviews,
Vol. 211,
Issue. ,
p.
103350.
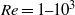 ) and on sub-horizontal walls (
) and on sub-horizontal walls (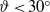 ). We analytically and numerically develop the stability analysis of an inclined melting–freezing interface bounding a free-surface laminar flow. The complete solution of both the linearized flow field and the heat conservation equations allows the exact derivation of the upper and lower temperature gradients at the interface, as required by the Stefan condition, from which the dispersion relationship is obtained. The eigenstructure is obtained and discussed. Free-surface dynamics appears to be crucial for the triggering of upstream propagating ice ripples, which grow at the liquid–solid interface. The kinematic and the dynamic conditions play a key role in controlling the formation of the free-surface fluctuations; these latter induce a streamline distortion with an increment of the wall-normal velocities and a destabilizing phase shift in the net heat transfer to the interface. Three-dimensional effects appear to be crucial at high Reynolds numbers. The role of inertia forces, vorticity, and thermal boundary conditions are also discussed.
). We analytically and numerically develop the stability analysis of an inclined melting–freezing interface bounding a free-surface laminar flow. The complete solution of both the linearized flow field and the heat conservation equations allows the exact derivation of the upper and lower temperature gradients at the interface, as required by the Stefan condition, from which the dispersion relationship is obtained. The eigenstructure is obtained and discussed. Free-surface dynamics appears to be crucial for the triggering of upstream propagating ice ripples, which grow at the liquid–solid interface. The kinematic and the dynamic conditions play a key role in controlling the formation of the free-surface fluctuations; these latter induce a streamline distortion with an increment of the wall-normal velocities and a destabilizing phase shift in the net heat transfer to the interface. Three-dimensional effects appear to be crucial at high Reynolds numbers. The role of inertia forces, vorticity, and thermal boundary conditions are also discussed.