Article contents
Inertia–gravity waves in inertially stable and unstable shear flows
Published online by Cambridge University Press: 19 June 2015
Abstract
An inertia–gravity wave (IGW) propagating in a vertically sheared, rotating stratified fluid interacts with the pair of inertial levels that surround the critical level. An exact expression for the form of the IGW is derived here in the case of a linear shear and used to examine this interaction in detail. This expression recovers the classical values of the transmission and reflection coefficients 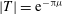 $|T|=\text{e}^{-{\rm\pi}{\it\mu}}$ and
$|T|=\text{e}^{-{\rm\pi}{\it\mu}}$ and 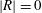 $|R|=0$ , where
$|R|=0$ , where 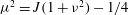 ${\it\mu}^{2}=J(1+{\it\nu}^{2})-1/4$ ,
${\it\mu}^{2}=J(1+{\it\nu}^{2})-1/4$ , 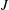 $J$ is the Richardson number and
$J$ is the Richardson number and  ${\it\nu}$ the ratio between the horizontal transverse and along-shear wavenumbers. For large
${\it\nu}$ the ratio between the horizontal transverse and along-shear wavenumbers. For large 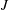 $J$ , a WKB analysis provides an interpretation of this result in term of tunnelling: an IGW incident on the lower inertial level becomes evanescent between the inertial levels, returning to an oscillatory behaviour above the upper inertial level. The amplitude of the transmitted wave is directly related to the decay of the evanescent solution between the inertial levels. In the immediate vicinity of the critical level, the evanescent IGW is well represented by the quasi-geostrophic approximation, so that the process can be interpreted as resulting from the coupling between balanced and unbalanced motion. The exact and WKB solutions describe the so-called valve effect, a dependence of the behaviour in the region between the inertial levels on the direction of wave propagation. For
$J$ , a WKB analysis provides an interpretation of this result in term of tunnelling: an IGW incident on the lower inertial level becomes evanescent between the inertial levels, returning to an oscillatory behaviour above the upper inertial level. The amplitude of the transmitted wave is directly related to the decay of the evanescent solution between the inertial levels. In the immediate vicinity of the critical level, the evanescent IGW is well represented by the quasi-geostrophic approximation, so that the process can be interpreted as resulting from the coupling between balanced and unbalanced motion. The exact and WKB solutions describe the so-called valve effect, a dependence of the behaviour in the region between the inertial levels on the direction of wave propagation. For 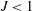 $J<1$ this is shown to lead to an amplification of the wave between the inertial levels. Since the flow is inertially unstable for
$J<1$ this is shown to lead to an amplification of the wave between the inertial levels. Since the flow is inertially unstable for 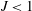 $J<1$ , this establishes a correspondence between the inertial-level interaction and the condition for inertial instability.
$J<1$ , this establishes a correspondence between the inertial-level interaction and the condition for inertial instability.
Information
- Type
- Papers
- Information
- Copyright
- © 2015 Cambridge University Press
References
- 2
- Cited by


