Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Mathis, S.
Alvan, L.
Remus, F.
Hennebelle, P.
and
Charbonnel, C.
2013.
Internal waves and tides in star-planet systems.
EAS Publications Series,
Vol. 62,
Issue. ,
p.
323.
Kong, Dali
Liao, Xinhao
and
Zhang, Keke
2014.
The sidewall-localized mode in a resonant precessing cylinder.
Physics of Fluids,
Vol. 26,
Issue. 5,
Kitchatinov, L. L.
2014.
BAROCLINIC INSTABILITY IN STELLAR RADIATION ZONES.
The Astrophysical Journal,
Vol. 784,
Issue. 1,
p.
81.
Vantieghem, S.
2014.
Inertial modes in a rotating triaxial ellipsoid.
Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 470,
Issue. 2168,
p.
20140093.
Favier, B.
Barker, A. J.
Baruteau, C.
and
Ogilvie, G. I.
2014.
Non-linear evolution of tidally forced inertial waves in rotating fluid bodies.
Monthly Notices of the Royal Astronomical Society,
Vol. 439,
Issue. 1,
p.
845.
Vogt, Tobias
Räbiger, Dirk
and
Eckert, Sven
2014.
Inertial wave dynamics in a rotating liquid metal.
Journal of Fluid Mechanics,
Vol. 753,
Issue. ,
p.
472.
Rabitti, Anna
and
Maas, Leo R. M.
2014.
Inertial wave rays in rotating spherical fluid domains.
Journal of Fluid Mechanics,
Vol. 758,
Issue. ,
p.
621.
Jouve, Laurène
and
Ogilvie, Gordon I.
2014.
Direct numerical simulations of an inertial wave attractor in linear and nonlinear regimes.
Journal of Fluid Mechanics,
Vol. 745,
Issue. ,
p.
223.
Ogilvie, Gordon I.
2014.
Tidal Dissipation in Stars and Giant Planets.
Annual Review of Astronomy and Astrophysics,
Vol. 52,
Issue. 1,
p.
171.
Ivers, D. J.
Jackson, A.
and
Winch, D.
2015.
Enumeration, orthogonality and completeness of the incompressible Coriolis modes in a sphere.
Journal of Fluid Mechanics,
Vol. 766,
Issue. ,
p.
468.
Mirouh, Giovanni M.
Baruteau, Clément
Rieutord, Michel
Ballot, Jérôme
García, R.A.
and
Ballot, J.
2015.
Gravito-inertial modes in a differentially rotating spherical shell.
EPJ Web of Conferences,
Vol. 101,
Issue. ,
p.
06046.
Mathis, S.
2015.
Variation of tidal dissipation in the convective envelope of low-mass stars along their evolution.
Astronomy & Astrophysics,
Vol. 580,
Issue. ,
p.
L3.
Auclair Desrotour, P.
Mathis, S.
and
Le Poncin-Lafitte, C.
2015.
Scaling laws to understand tidal dissipation in fluid planetary regions and stars I. Rotation, stratification and thermal diffusivity.
Astronomy & Astrophysics,
Vol. 581,
Issue. ,
p.
A118.
Guenel, M.
Baruteau, C.
Mathis, S.
and
Rieutord, M.
2016.
Tidal inertial waves in differentially rotating convective envelopes of low-mass stars.
Astronomy & Astrophysics,
Vol. 589,
Issue. ,
p.
A22.
Lanza, A. F.
and
Mathis, S.
2016.
Tides and angular momentum redistribution inside low-mass stars hosting planets: a first dynamical model.
Celestial Mechanics and Dynamical Astronomy,
Vol. 126,
Issue. 1-3,
p.
249.
Bolmont, Emeline
and
Mathis, Stéphane
2016.
Effect of the rotation and tidal dissipation history of stars on the evolution of close-in planets.
Celestial Mechanics and Dynamical Astronomy,
Vol. 126,
Issue. 1-3,
p.
275.
Hoff, Michael
Harlander, Uwe
and
Triana, Santiago Andrés
2016.
Study of turbulence and interacting inertial modes in a differentially rotating spherical shell experiment.
Physical Review Fluids,
Vol. 1,
Issue. 4,
Mirouh, G. M.
Baruteau, C.
Rieutord, M.
and
Ballot, J.
2016.
Gravito-inertial waves in a differentially rotating spherical shell.
Journal of Fluid Mechanics,
Vol. 800,
Issue. ,
p.
213.
Mathis, S.
Auclair-Desrotour, P.
Guenel, M.
Gallet, F.
and
Le Poncin-Lafitte, C.
2016.
The impact of rotation on turbulent tidal friction in stellar and planetary convective regions.
Astronomy & Astrophysics,
Vol. 592,
Issue. ,
p.
A33.
Mathis, Stéphane
2017.
Handbook of Exoplanets.
p.
1.
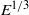 ${E}^{1/ 3} $ with the Ekman number
${E}^{1/ 3} $ with the Ekman number 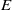 $E$ , as in the solid-body rotation case. There also exist modes with thin detached layers of width scaling with
$E$ , as in the solid-body rotation case. There also exist modes with thin detached layers of width scaling with 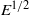 ${E}^{1/ 2} $ as Ekman boundary layers. The behaviour of inertial waves with a corotation resonance within the shell is also considered. For cylindrical rotation, waves get dramatically absorbed at corotation. In contrast, for shellular rotation, waves may cross a critical layer without visible absorption, and such modes can be unstable for small enough Ekman numbers.
${E}^{1/ 2} $ as Ekman boundary layers. The behaviour of inertial waves with a corotation resonance within the shell is also considered. For cylindrical rotation, waves get dramatically absorbed at corotation. In contrast, for shellular rotation, waves may cross a critical layer without visible absorption, and such modes can be unstable for small enough Ekman numbers.
