Article contents
Instability of pressure-driven gas–liquid two-layer channel flows in two and three dimensions
Published online by Cambridge University Press: 15 June 2018
Abstract
We study unstable waves in gas–liquid two-layer channel flows driven by a pressure gradient, under stable stratification, not assumed to be set in motion impulsively. The basis of the study is direct numerical simulation (DNS) of the two-phase Navier–Stokes equations in two and three dimensions for moderately large Reynolds numbers, accompanied by a theoretical description of the dynamics in the linear regime (Orr–Sommerfeld–Squire equations). The results are compared and contrasted across a range of density ratios 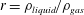 $r=\unicode[STIX]{x1D70C}_{liquid}/\unicode[STIX]{x1D70C}_{gas}$. Linear theory indicates that the growth rate of small-amplitude interfacial disturbances generally decreases with increasing
$r=\unicode[STIX]{x1D70C}_{liquid}/\unicode[STIX]{x1D70C}_{gas}$. Linear theory indicates that the growth rate of small-amplitude interfacial disturbances generally decreases with increasing  $r$; at the same time, the cutoff wavenumbers in both streamwise and spanwise directions increase, leading to an ever-increasing range of unstable wavenumbers, albeit with diminished growth rates. The analysis also demonstrates that the most dangerous mode is two-dimensional in all cases considered. The results of a comparison between the DNS and linear theory demonstrate a consistency between the two approaches: as such, the route to a three-dimensional flow pattern is direct in these cases, i.e. through the strong influence of the linear instability. We also characterize the nonlinear behaviour of the system, and we establish that the disturbance vorticity field in two-dimensional systems is consistent with a mechanism proposed previously by Hinch (J. Fluid Mech., vol. 144, 1984, p. 463) for weakly inertial flows. A flow-pattern map constructed from two-dimensional numerical simulations is used to describe the various flow regimes observed as a function of density ratio, Reynolds number and Weber number. Corresponding simulations in three dimensions confirm that the flow-pattern map can be used to infer the fate of the interface there also, and show strong three-dimensionality in cases that exhibit violent behaviour in two dimensions, or otherwise the development of behaviour that is nearly two-dimensional behaviour possibly with the formation of a capillary ridge. The three-dimensional vorticity field is also analysed, thereby demonstrating how streamwise vorticity arises from the growth of otherwise two-dimensional modes.
$r$; at the same time, the cutoff wavenumbers in both streamwise and spanwise directions increase, leading to an ever-increasing range of unstable wavenumbers, albeit with diminished growth rates. The analysis also demonstrates that the most dangerous mode is two-dimensional in all cases considered. The results of a comparison between the DNS and linear theory demonstrate a consistency between the two approaches: as such, the route to a three-dimensional flow pattern is direct in these cases, i.e. through the strong influence of the linear instability. We also characterize the nonlinear behaviour of the system, and we establish that the disturbance vorticity field in two-dimensional systems is consistent with a mechanism proposed previously by Hinch (J. Fluid Mech., vol. 144, 1984, p. 463) for weakly inertial flows. A flow-pattern map constructed from two-dimensional numerical simulations is used to describe the various flow regimes observed as a function of density ratio, Reynolds number and Weber number. Corresponding simulations in three dimensions confirm that the flow-pattern map can be used to infer the fate of the interface there also, and show strong three-dimensionality in cases that exhibit violent behaviour in two dimensions, or otherwise the development of behaviour that is nearly two-dimensional behaviour possibly with the formation of a capillary ridge. The three-dimensional vorticity field is also analysed, thereby demonstrating how streamwise vorticity arises from the growth of otherwise two-dimensional modes.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 3
- Cited by


