1. Introduction
In colloidal science, coating surfaces with a polymer ‘brush’ is an effective stabilisation strategy, preventing coagulation in suspensions, as was first suggested by van der Waarden (Reference van der Waarden1950). Polymer brushes are also extensively used as protective layers that resist adsorption of undesired materials onto surfaces (Halperin Reference Halperin1999; Ma et al. Reference Ma, Zhang, Yu and Zhou2019; Yan, Bockstaller & Matyjaszewski Reference Yan, Bockstaller and Matyjaszewski2020). In particular, membranes used for separation processes are prone to unwanted material deposition, exacerbated by the flow through the membranes. Hence, polymer brush coatings have been considered as a promising strategy for fouling prevention (Keating, Imbrogno & Belfort Reference Keating, Imbrogno and Belfort2016; Werber, Osuji & Elimelech Reference Werber, Osuji and Elimelech2016). These grafted polymers are known primarily for their ability to exert a repulsive force when compressed (Milner Reference Milner1989); however, they also affect the hydrodynamic interaction between surfaces. Fredrickson & Pincus (Reference Fredrickson and Pincus1991) modelled the effect of a polymer brush on the hydrodynamic force acting on a particle approaching a stationary impermeable surface. Their analysis assumed a highly compressed brush, i.e. a low-permeability brush, modelled as a porous medium squeezed between the two surfaces, for which the flow may be described by the Brinkman equation, employing lubrication theory. In particular, the model assumed that the brush is so dense, translated to an extremely low permeability, that the velocity distribution in it resembles a ‘plug flow’. Potanin & Russel (Reference Potanin and Russel1995) relaxed this assumption and, using lubrication theory with a full solution of the Brinkman equation, numerically calculated the hydrodynamic force as a function of separation distance and provided analytic expressions for limiting cases. Both Fredrickson & Pincus (Reference Fredrickson and Pincus1991) and Potanin & Russel (Reference Potanin and Russel1995) showed how the presence of a polymer layer in the thin gap between surfaces significantly increases the hydrodynamic force.
It is well known that the lubrication interaction of a particle in proximity to a planar surface induces a force that may be either attractive or repulsive, depending on the direction of relative motion. Brenner (Reference Brenner1961) first solved the case of a particle moving towards a planar impenetrable surface. This result was then extended to permeable surfaces by Goren (Reference Goren1979), demonstrating that surface permeability eliminates the singularity at contact, with the force attaining a constant value that depends on the particle size and the permeability of the surface. Knox et al. (Reference Knox, Wilson, Duffy and McKee2015) and Venerus (Reference Venerus2018) studied the squeeze flow between porous disks, and in the context of membrane separation, most relevant for the present work, this problem was studied by Ramon & Hoek (Reference Ramon and Hoek2012) and Ramon et al. (Reference Ramon, Huppert, Lister and Stone2013), who employed a lubrication approach and derived asymptotic solutions for the attractive force between a solid spherical particle and a permeable boundary (further analysis of this problem may be found, for example, in Knox et al. (Reference Knox, Duffy, McKee and Wilson2017) and in the references listed in Ramon et al. (Reference Ramon, Huppert, Lister and Stone2013)).
Here, we study the hydrodynamic force on a particle as affected by the presence of a polymer brush coating a permeable surface (e.g. a filtration membrane), and the interplay of this force and the steric repulsion exerted by the brush upon compression. A lubrication model is formulated, from which the pressure field and the force are evaluated. The characteristics of the brush layer and the steric force it exerts are outlined. An asymptotic analysis is performed for various limiting cases. Finally, we consider the equilibrium position of the particle under the opposing action of the two forces.
2. Model formulation
We consider a spherical particle with radius ![]() $R$ in proximity to a planar membrane, with permeance (permeability per unit thickness)
$R$ in proximity to a planar membrane, with permeance (permeability per unit thickness) ![]() $k$, covered by a polymer brush layer of average thickness
$k$, covered by a polymer brush layer of average thickness ![]() $h_{0}$. We assume that there are no chemical reactions between the particle and polymer, and that the polymer chains are of equal length and are in contact with a good solvent. A background pressure
$h_{0}$. We assume that there are no chemical reactions between the particle and polymer, and that the polymer chains are of equal length and are in contact with a good solvent. A background pressure ![]() $p_0$ drives a permeation rate
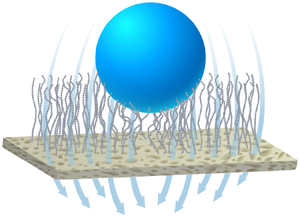
$p_0$ drives a permeation rate ![]() $V_{0}$ through the membrane. The particle, advected by the flow, makes contact with the polymer brush layer, which exerts a repulsive force as it is compressed, acting to keep the particle away from the membrane. In what follows, we are interested in the attractive hydrodynamic force exerted by the flow and the equilibrium that may exist between it and the repulsive force of the brush as it is compressed (see figure 1 for a schematic illustration).
$V_{0}$ through the membrane. The particle, advected by the flow, makes contact with the polymer brush layer, which exerts a repulsive force as it is compressed, acting to keep the particle away from the membrane. In what follows, we are interested in the attractive hydrodynamic force exerted by the flow and the equilibrium that may exist between it and the repulsive force of the brush as it is compressed (see figure 1 for a schematic illustration).

Figure 1. Schematic illustration of the system. A particle of radius ![]() $R$ near a membrane (with permeance
$R$ near a membrane (with permeance ![]() $k$) through which a velocity
$k$) through which a velocity ![]() $V_{0}$ is induced. The particle compresses a polymer brush of initial thickness
$V_{0}$ is induced. The particle compresses a polymer brush of initial thickness ![]() $h_{0}$. The gap between the particle and the membrane is
$h_{0}$. The gap between the particle and the membrane is ![]() $h(r)\approx \delta +r^{2}/2R$, where
$h(r)\approx \delta +r^{2}/2R$, where ![]() $\delta$ is the distance of closest approach. In the diagram,
$\delta$ is the distance of closest approach. In the diagram, ![]() $\ell \ (\equiv \varGamma ^{-1/2}, \text{ where } \varGamma \text{ is the `graft density'})$ is the distance between graft points of the polymer at the surface,
$\ell \ (\equiv \varGamma ^{-1/2}, \text{ where } \varGamma \text{ is the `graft density'})$ is the distance between graft points of the polymer at the surface, ![]() $a$ is the ‘effective’ monomer diameter and
$a$ is the ‘effective’ monomer diameter and ![]() $\xi$ is the ‘correlation length’, representing the average distance between chains.
$\xi$ is the ‘correlation length’, representing the average distance between chains.
The hydrodynamic force on the particle, induced by the flow through the brush and the underlying membrane, is calculated in the lubrication limit by integrating the pressure along the particle surface, which is approximated by the shape ![]() $h(r)=\delta +r^{2}/2R$, where
$h(r)=\delta +r^{2}/2R$, where ![]() $\delta$ denotes the distance of closest approach. In what follows, a lubrication equation is derived, from which the pressure distribution may be evaluated. We begin with the equations for the steady-state velocity field within the gap confined between the particle and the membrane, in the lubrication limit, namely, the axisymmetric, incompressible continuity and Brinkman equations, given in scaled form as
$\delta$ denotes the distance of closest approach. In what follows, a lubrication equation is derived, from which the pressure distribution may be evaluated. We begin with the equations for the steady-state velocity field within the gap confined between the particle and the membrane, in the lubrication limit, namely, the axisymmetric, incompressible continuity and Brinkman equations, given in scaled form as
These equations are valid when ![]() $h_{0}/R \equiv \varepsilon \ll 1$, where
$h_{0}/R \equiv \varepsilon \ll 1$, where ![]() $h_{0}\approx N\varGamma ^{1/3}a^{5/3}$ is the brush thickness at equilibrium (Halperin Reference Halperin1999), with
$h_{0}\approx N\varGamma ^{1/3}a^{5/3}$ is the brush thickness at equilibrium (Halperin Reference Halperin1999), with ![]() $\varGamma \equiv \ell ^{-2}$ denoting the graft density, i.e. the number of polymer chains per unit area,
$\varGamma \equiv \ell ^{-2}$ denoting the graft density, i.e. the number of polymer chains per unit area, ![]() $a$ is the ‘effective’ monomer size and
$a$ is the ‘effective’ monomer size and ![]() $N$ is the number of monomers in a chain (see figure 1). Here,
$N$ is the number of monomers in a chain (see figure 1). Here, ![]() $u$ and
$u$ and ![]() $v$ are the respective
$v$ are the respective ![]() $r$ and
$r$ and ![]() $z$ velocity components, scaled by
$z$ velocity components, scaled by ![]() $\varepsilon ^{-1}V_0$ and
$\varepsilon ^{-1}V_0$ and ![]() $V_0$, respectively, and
$V_0$, respectively, and ![]() $p$ is the pressure, scaled by
$p$ is the pressure, scaled by ![]() $\mu V_0 R/\varepsilon h_0$, where
$\mu V_0 R/\varepsilon h_0$, where ![]() $\mu$ is the viscosity. Further,
$\mu$ is the viscosity. Further, ![]() $r$ is scaled by
$r$ is scaled by ![]() $(2R h_0)^{1/2}$, while
$(2R h_0)^{1/2}$, while ![]() $z$,
$z$, ![]() $h$ and
$h$ and ![]() $\delta$ are scaled by
$\delta$ are scaled by ![]() $h_0$. The permeability in the Brinkman equations is here represented by the ‘correlation length’,
$h_0$. The permeability in the Brinkman equations is here represented by the ‘correlation length’,
an important parameter in polymer physics, which characterises the distance over which interactions occur mostly between segments of the same chain (Rubinstein & Colby Reference Rubinstein and Colby2003). As such, ![]() $\xi$ represents an average distance between chains, and so
$\xi$ represents an average distance between chains, and so ![]() $\xi ^{2}$ provides an estimate of the ‘pore’ dimensions and is used as a proxy of a permeability coefficient (Milner Reference Milner1989; Fredrickson & Pincus Reference Fredrickson and Pincus1991). With this definition, the brush permeance,
$\xi ^{2}$ provides an estimate of the ‘pore’ dimensions and is used as a proxy of a permeability coefficient (Milner Reference Milner1989; Fredrickson & Pincus Reference Fredrickson and Pincus1991). With this definition, the brush permeance, ![]() $k_p$, in dimensionless form, is the parameter
$k_p$, in dimensionless form, is the parameter ![]() $\varLambda \equiv (2\xi _{0}/h_{0})^{2}=4k_{p}/h_{0}$, where
$\varLambda \equiv (2\xi _{0}/h_{0})^{2}=4k_{p}/h_{0}$, where ![]() $\xi _{0}=\xi |_{h=h_{0}}=\varGamma ^{-1/2}$ is the characteristic scale for the correlation length.
$\xi _{0}=\xi |_{h=h_{0}}=\varGamma ^{-1/2}$ is the characteristic scale for the correlation length.
Potanin & Russel (Reference Potanin and Russel1995) derived a solution for ![]() $u(r,z)$ by solving (2.2) inside and outside the polymer brush layer, the result of which is mathematically complicated and does not lend itself to derivation of analytic approximations using asymptotic analysis. To facilitate the present analysis, we focus on the ‘lubricating region’, i.e. a region of scale
$u(r,z)$ by solving (2.2) inside and outside the polymer brush layer, the result of which is mathematically complicated and does not lend itself to derivation of analytic approximations using asymptotic analysis. To facilitate the present analysis, we focus on the ‘lubricating region’, i.e. a region of scale ![]() $(Rh_{0})^{1/2}$ about the point of closest approach, responsible for most of the hydrodynamic interaction. We assume that in this region the particle is in contact with the polymer brush, and hence the velocity is calculated only inside the brush layer. This invariably results, to some extent, in an overestimation of the forces on the particle at large values of
$(Rh_{0})^{1/2}$ about the point of closest approach, responsible for most of the hydrodynamic interaction. We assume that in this region the particle is in contact with the polymer brush, and hence the velocity is calculated only inside the brush layer. This invariably results, to some extent, in an overestimation of the forces on the particle at large values of ![]() $\delta$. With this assumption, the solution to (2.2), subjected to the no-slip boundary conditions,
$\delta$. With this assumption, the solution to (2.2), subjected to the no-slip boundary conditions, ![]() $u|_{z=0}=u|_{z=h(r)}=0$, is
$u|_{z=0}=u|_{z=h(r)}=0$, is
which, when substituted into (2.1) and integrated with respect to ![]() $z$, yields the lubrication equation
$z$, yields the lubrication equation
where ![]() $\alpha =2Rk/h_{0}^{2}$. The boundary conditions for (2.5) require that the pressure decays to zero in the far field and that symmetry about the centreline is maintained, i.e.
$\alpha =2Rk/h_{0}^{2}$. The boundary conditions for (2.5) require that the pressure decays to zero in the far field and that symmetry about the centreline is maintained, i.e.
Finally, the hydrodynamic force is calculated using
 \begin{equation} F_{h}=2{\rm \pi}\int\limits_{0}^{\infty}rp(r)\,\mathrm{d}r, \end{equation}
\begin{equation} F_{h}=2{\rm \pi}\int\limits_{0}^{\infty}rp(r)\,\mathrm{d}r, \end{equation}2.1. Steric repulsion through polymer brush compression
The flow driven through the membrane carries particles towards it. However, once a particle makes contact with a brush, which is too dense for it to penetrate (i.e. satisfying ![]() $R\gg \xi$ (Halperin Reference Halperin1999)), it compresses the brush, resulting in a repulsive force. Following de Gennes (Reference de Gennes1980), this force may be evaluated, in the limit
$R\gg \xi$ (Halperin Reference Halperin1999)), it compresses the brush, resulting in a repulsive force. Following de Gennes (Reference de Gennes1980), this force may be evaluated, in the limit ![]() $h_{0}\ll R$, as
$h_{0}\ll R$, as
 \begin{equation} F_{s}=\int\limits_{A}\varPi\,\mathrm{d}A =2{\rm \pi} R h_{0}\int\limits_{\delta}^{1}\varPi(z)\,\mathrm{d}z, \end{equation}
\begin{equation} F_{s}=\int\limits_{A}\varPi\,\mathrm{d}A =2{\rm \pi} R h_{0}\int\limits_{\delta}^{1}\varPi(z)\,\mathrm{d}z, \end{equation}
where ![]() $A$ is the area of contact. Here,
$A$ is the area of contact. Here, ![]() $\varPi$ is the osmotic pressure, given by the scaling theory of semidilute polymer solutions (Alexander Reference Alexander1977; de Gennes Reference de Gennes1980) as
$\varPi$ is the osmotic pressure, given by the scaling theory of semidilute polymer solutions (Alexander Reference Alexander1977; de Gennes Reference de Gennes1980) as
where ![]() $k_{B}$ is Boltzmann's constant and
$k_{B}$ is Boltzmann's constant and ![]() $T$ is the absolute temperature. Combining (2.8) and (2.9), the non-dimensional steric force is (Klein et al. Reference Klein, Kumacheva, Mahalu, Perahla and Fetters1994)
$T$ is the absolute temperature. Combining (2.8) and (2.9), the non-dimensional steric force is (Klein et al. Reference Klein, Kumacheva, Mahalu, Perahla and Fetters1994)
which is here scaled by ![]() $8{\rm \pi} R h_0 k_{B} T\varGamma ^{3/2}/35$. The steric force (2.10) holds for
$8{\rm \pi} R h_0 k_{B} T\varGamma ^{3/2}/35$. The steric force (2.10) holds for ![]() $0<\delta \leqslant 1$ and is identically zero when
$0<\delta \leqslant 1$ and is identically zero when ![]() $\delta =1$, i.e. when the particle does not yet compress the brush.
$\delta =1$, i.e. when the particle does not yet compress the brush.
3. Asymptotic analysis
Generally, the pressure field provided by (2.5) may only be evaluated numerically. In what follows, we derive analytic solutions for various limiting cases. The scaled permeance of the brush is given by ![]() $\varLambda \propto k_{p}/h_{0}$, for which two cases are treated: (i) a ‘dilute’ brush (
$\varLambda \propto k_{p}/h_{0}$, for which two cases are treated: (i) a ‘dilute’ brush (![]() $\varLambda \gg 1$), perturbed near a base state in which the brush is absent; and (ii) a ‘dense’ brush, for which the base state depends on whether the dominant resistance to flow comes from the brush or the membrane. In the asymptotic analysis, the scaled membrane permeance is small,
$\varLambda \gg 1$), perturbed near a base state in which the brush is absent; and (ii) a ‘dense’ brush, for which the base state depends on whether the dominant resistance to flow comes from the brush or the membrane. In the asymptotic analysis, the scaled membrane permeance is small, ![]() $\alpha \ll 1$. While the asymptotic solutions provide the pressure field, these are not shown here explicitly since we seek the hydrodynamic force, found by integrating the pressure over the particle surface via (2.7).
$\alpha \ll 1$. While the asymptotic solutions provide the pressure field, these are not shown here explicitly since we seek the hydrodynamic force, found by integrating the pressure over the particle surface via (2.7).
3.1. Dilute brush  $(\varLambda\gg1)$
$(\varLambda\gg1)$
In the case of a ‘dilute’ brush, characterised by a small graft density ![]() $\varGamma$, the pressure may be expanded as
$\varGamma$, the pressure may be expanded as ![]() $p(r,\varLambda )=p_{0}(r)+\varLambda ^{-1}p_{1}(r)+O(\varLambda ^{-2})$, where
$p(r,\varLambda )=p_{0}(r)+\varLambda ^{-1}p_{1}(r)+O(\varLambda ^{-2})$, where ![]() $p_0$ is the pressure field in the absence of a brush. Furthermore,
$p_0$ is the pressure field in the absence of a brush. Furthermore,
Including the membrane permeance in this case is achieved by assuming ![]() $\alpha \approx \varLambda ^{-1}$, leading to a set of perturbation problems, written here to
$\alpha \approx \varLambda ^{-1}$, leading to a set of perturbation problems, written here to ![]() $O(\varLambda ^{-2})$ as
$O(\varLambda ^{-2})$ as
 \begin{equation} \frac{1}{12r}\frac{\mathrm{d}}{\mathrm{d}r} \left[rh^{3}\frac{\mathrm{d}p_{i}}{\mathrm{d}r}\right]= \begin{cases} -1, & i=0, \\ \varLambda\alpha p_{i-1}+\dfrac{1}{30r}\dfrac{\mathrm{d}}{\mathrm{d}r} \left[rh^{7/2}\dfrac{\mathrm{d}p_{i-1}}{\mathrm{d}r}\right],\quad & i=1,\\ \varLambda\alpha p_{i-1}+\dfrac{1}{30r}\dfrac{\mathrm{d}}{\mathrm{d}r} \left[rh^{7/2}\dfrac{\mathrm{d}p_{i-1}}{\mathrm{d}r}\right]-\dfrac{17}{1260r} \dfrac{\mathrm{d}}{\mathrm{d}r} \left[rh^{4}\dfrac{\mathrm{d}p_{i-2}}{\mathrm{d}r}\right], & i=2, \end{cases} \end{equation}
\begin{equation} \frac{1}{12r}\frac{\mathrm{d}}{\mathrm{d}r} \left[rh^{3}\frac{\mathrm{d}p_{i}}{\mathrm{d}r}\right]= \begin{cases} -1, & i=0, \\ \varLambda\alpha p_{i-1}+\dfrac{1}{30r}\dfrac{\mathrm{d}}{\mathrm{d}r} \left[rh^{7/2}\dfrac{\mathrm{d}p_{i-1}}{\mathrm{d}r}\right],\quad & i=1,\\ \varLambda\alpha p_{i-1}+\dfrac{1}{30r}\dfrac{\mathrm{d}}{\mathrm{d}r} \left[rh^{7/2}\dfrac{\mathrm{d}p_{i-1}}{\mathrm{d}r}\right]-\dfrac{17}{1260r} \dfrac{\mathrm{d}}{\mathrm{d}r} \left[rh^{4}\dfrac{\mathrm{d}p_{i-2}}{\mathrm{d}r}\right], & i=2, \end{cases} \end{equation}
in which the term ![]() $\alpha \varLambda =O(1)$, with
$\alpha \varLambda =O(1)$, with ![]() $\alpha \neq \varLambda ^{-1}$ necessarily. Three (and more) terms may be calculated for the expansion of
$\alpha \neq \varLambda ^{-1}$ necessarily. Three (and more) terms may be calculated for the expansion of ![]() $p$; however, only the first two terms yield analytic expressions for the force. The hydrodynamic force in this case is
$p$; however, only the first two terms yield analytic expressions for the force. The hydrodynamic force in this case is
in which the leading-order term recovers the result of Brenner (Reference Brenner1961) for the force on a sphere approaching an impermeable surface. The second and third terms are the ![]() $O(\varLambda ^{-1})$ correction to this classical result, where the second term recovers the result of Goren (Reference Goren1979) and Ramon et al. (Reference Ramon, Huppert, Lister and Stone2013), showing that a finite permeance decreases the force, and the third term is a new correction representing the addition of the polymer brush on the surface, which increases the force.
$O(\varLambda ^{-1})$ correction to this classical result, where the second term recovers the result of Goren (Reference Goren1979) and Ramon et al. (Reference Ramon, Huppert, Lister and Stone2013), showing that a finite permeance decreases the force, and the third term is a new correction representing the addition of the polymer brush on the surface, which increases the force.
3.2. Dense brush  $(\varLambda\ll1)$
$(\varLambda\ll1)$
In the case of a dense brush, the hyperbolic tangent term in (2.5) is approximately ![]() $\varLambda ^{1/2}\xi /h$. If
$\varLambda ^{1/2}\xi /h$. If ![]() $\varLambda ,\alpha \ll 1$, however, the pressure in (2.5) must be rescaled to avoid a singularity in the leading-order lubrication equation. We begin by rescaling the coordinate
$\varLambda ,\alpha \ll 1$, however, the pressure in (2.5) must be rescaled to avoid a singularity in the leading-order lubrication equation. We begin by rescaling the coordinate ![]() $r=\delta ^{1/2}\eta$, to obtain
$r=\delta ^{1/2}\eta$, to obtain
Next, we define a new dimensionless parameter,
and identify two possible scenarios: ![]() $\beta \ll 1$, i.e. the membrane permeance is much smaller than that of the polymer brush,
$\beta \ll 1$, i.e. the membrane permeance is much smaller than that of the polymer brush, ![]() $k\ll \varepsilon k_{p}$; and
$k\ll \varepsilon k_{p}$; and ![]() $\beta \gg 1$, for which the permeance ratio between the membrane and brush satisfies
$\beta \gg 1$, for which the permeance ratio between the membrane and brush satisfies ![]() $k/k_{p}\gg \varepsilon$.
$k/k_{p}\gg \varepsilon$.
3.2.1. The case  $\beta \ll 1$
$\beta \ll 1$
In this limit the brush layer permeance, however small, is still much larger than that of the membrane it covers. The pressure is rescaled as ![]() $P=\varLambda \delta ^{3/2}p/4$ and (3.4) becomes
$P=\varLambda \delta ^{3/2}p/4$ and (3.4) becomes
The asymptotic order of ![]() $\alpha /\beta \propto \varLambda \ll 1$ is indeterminate. The effect of reducing the brush density is found by assuming
$\alpha /\beta \propto \varLambda \ll 1$ is indeterminate. The effect of reducing the brush density is found by assuming ![]() $\alpha = O(\beta ^{3})$ and expanding the pressure as
$\alpha = O(\beta ^{3})$ and expanding the pressure as ![]() $P=P_{0}(\eta )+\beta P_{1}(\eta )+O(\beta ^{2})$. For convenience, we define
$P=P_{0}(\eta )+\beta P_{1}(\eta )+O(\beta ^{2})$. For convenience, we define
such that (3.6) may be written as
 \begin{equation} \frac{1}{\eta}\frac{\mathrm{d}}{\mathrm{d}\eta} \left[\eta(1+\eta^{2})^{5/2}\dfrac{\mathrm{d}P_{i}}{\mathrm{d}r}\right]= \begin{cases} -1, & i=0,\\ P_{i-1}+\dfrac{\gamma}{\eta}\dfrac{\mathrm{d}}{\mathrm{d}\eta} \left[\eta(1+\eta^{2})^{9/4}\dfrac{\mathrm{d}P_{i-1}}{\mathrm{d}r}\right], & i\geqslant 1. \end{cases} \end{equation}
\begin{equation} \frac{1}{\eta}\frac{\mathrm{d}}{\mathrm{d}\eta} \left[\eta(1+\eta^{2})^{5/2}\dfrac{\mathrm{d}P_{i}}{\mathrm{d}r}\right]= \begin{cases} -1, & i=0,\\ P_{i-1}+\dfrac{\gamma}{\eta}\dfrac{\mathrm{d}}{\mathrm{d}\eta} \left[\eta(1+\eta^{2})^{9/4}\dfrac{\mathrm{d}P_{i-1}}{\mathrm{d}r}\right], & i\geqslant 1. \end{cases} \end{equation} Here, an analytic expression for the force (2.7) may be found only to ![]() $O(\beta )$,
$O(\beta )$,
where the leading-order term recovers the ‘plug-flow’ result derived by Fredrickson & Pincus (Reference Fredrickson and Pincus1991), and the ![]() $O(\beta )$ term is the correction due to a finite (small) membrane permeance and a small increase in the brush permeance. While the membrane permeance clearly decreases the hydrodynamic force, lowering the brush density – which is expected to decrease this force – is here seen, in the
$O(\beta )$ term is the correction due to a finite (small) membrane permeance and a small increase in the brush permeance. While the membrane permeance clearly decreases the hydrodynamic force, lowering the brush density – which is expected to decrease this force – is here seen, in the ![]() $O(\beta )$ correction, to increase it. This is because, as
$O(\beta )$ correction, to increase it. This is because, as ![]() $\varLambda \rightarrow 0$, the polymer brush becomes impermeable, such that the flow is unaffected by the presence of the membrane. Decreasing the brush density ‘exposes’ the flow to the membrane, which is then less permeable than the brush. Consequently, the combined permeance (membrane and brush) decreases and the correction to the force is positive.
$\varLambda \rightarrow 0$, the polymer brush becomes impermeable, such that the flow is unaffected by the presence of the membrane. Decreasing the brush density ‘exposes’ the flow to the membrane, which is then less permeable than the brush. Consequently, the combined permeance (membrane and brush) decreases and the correction to the force is positive.
Rewriting (3.9) in terms of ![]() $\alpha$,
$\alpha$, ![]() $\varLambda$ and
$\varLambda$ and ![]() $\delta$ gives
$\delta$ gives
in which the requirement that the leading-order term dominates over the last term leads to ![]() $\delta \gg \varLambda ^{2}$ for which the correction is valid.
$\delta \gg \varLambda ^{2}$ for which the correction is valid.
3.2.2. The case  $\beta \gg 1$
$\beta \gg 1$
Here, the permeance ratio is ![]() $k/k_{p}\gg \varepsilon$ and the pressure is rescaled as
$k/k_{p}\gg \varepsilon$ and the pressure is rescaled as ![]() $\mathcal {P}=\alpha p$, so that
$\mathcal {P}=\alpha p$, so that
in which expanding ![]() $\mathcal {P}$ as a series of
$\mathcal {P}$ as a series of ![]() $\beta ^{-1}$ clearly results in a singular perturbation problem, with the leading-order solution
$\beta ^{-1}$ clearly results in a singular perturbation problem, with the leading-order solution ![]() $\mathcal {P}_{0}=1$ unable to satisfy the far-field boundary condition. We introduce yet another rescaled coordinate
$\mathcal {P}_{0}=1$ unable to satisfy the far-field boundary condition. We introduce yet another rescaled coordinate ![]() $\eta =\beta ^{1/3}\zeta$, with which (3.11) becomes
$\eta =\beta ^{1/3}\zeta$, with which (3.11) becomes
enabling a regular perturbation for ![]() $\beta ^{-2/3}\ll 1$ by expanding
$\beta ^{-2/3}\ll 1$ by expanding ![]() $\mathcal {P}(\zeta ,\beta )=\mathcal {P}_{0}(\zeta )+\beta ^{-2/3}$
$\mathcal {P}(\zeta ,\beta )=\mathcal {P}_{0}(\zeta )+\beta ^{-2/3}$ ![]() $\mathcal {P}_{1}(\zeta ) +O(\beta ^{-4/3})$. An analytic solution is found for the leading-order equation
$\mathcal {P}_{1}(\zeta ) +O(\beta ^{-4/3})$. An analytic solution is found for the leading-order equation
and the corresponding force, written in term of ![]() $\varLambda$,
$\varLambda$, ![]() $\alpha$ and
$\alpha$ and ![]() $\delta$, is
$\delta$, is
where ![]() $c=3^{1/6}\varGamma (1/3)^{2}/2^{2/3}\approx 5.43$.
$c=3^{1/6}\varGamma (1/3)^{2}/2^{2/3}\approx 5.43$.
The dependence of the hydrodynamic force, ![]() $F_h$, on the brush permeance,
$F_h$, on the brush permeance, ![]() $\varLambda$, is presented in figure 2(a), comparing the asymptotics with the numerical calculations. Figure 2(b) maps the asymptotic solutions from the current work, as well as those from previous studies, in the
$\varLambda$, is presented in figure 2(a), comparing the asymptotics with the numerical calculations. Figure 2(b) maps the asymptotic solutions from the current work, as well as those from previous studies, in the ![]() $\varLambda$–
$\varLambda$–![]() $\beta$ plane. Here, results appearing on the right end of the scale describe the absence of a brush. Meanwhile,
$\beta$ plane. Here, results appearing on the right end of the scale describe the absence of a brush. Meanwhile, ![]() $\beta$ marks the permeance ratio between the membrane and brush, such that low values denote a brush permeance much larger than that of the membrane.
$\beta$ marks the permeance ratio between the membrane and brush, such that low values denote a brush permeance much larger than that of the membrane.

Figure 2. (a) The hydrodynamic force, scaled by ![]() $F_{Stokes}=6{\rm \pi} \mu R V_{0}$, as a function of brush permeance,
$F_{Stokes}=6{\rm \pi} \mu R V_{0}$, as a function of brush permeance, ![]() $\varLambda \equiv 4k_{p}/h_{0}$, for
$\varLambda \equiv 4k_{p}/h_{0}$, for ![]() $\alpha =10^{-3}$. The red solid line is the numerical calculation, while the blue dashed, green dashed-dotted and violet dotted lines mark the asymptotic solutions (3.3), (3.10) and (3.14), respectively. (b) Mapping of the asymptotic solutions to (2.5) in the
$\alpha =10^{-3}$. The red solid line is the numerical calculation, while the blue dashed, green dashed-dotted and violet dotted lines mark the asymptotic solutions (3.3), (3.10) and (3.14), respectively. (b) Mapping of the asymptotic solutions to (2.5) in the ![]() $\varLambda$–
$\varLambda$–![]() $\beta$ plane. Black dots mark leading-order solutions; lines and shaded areas mark asymptotic solutions valid for a finite range of
$\beta$ plane. Black dots mark leading-order solutions; lines and shaded areas mark asymptotic solutions valid for a finite range of ![]() $\varLambda ,\beta$.
$\varLambda ,\beta$.
4. Equilibrium
When the hydrodynamic and steric forces are exactly balanced, the particle reaches its equilibrium position, which should be sufficiently away from the membrane surface so as to avoid performance deterioration (Keating et al. Reference Keating, Imbrogno and Belfort2016). In order to evaluate this balance, ![]() $F_{h}$ is rescaled by
$F_{h}$ is rescaled by ![]() $8{\rm \pi} R h_0 k_{B} T\varGamma ^{3/2}/35$, so that
$8{\rm \pi} R h_0 k_{B} T\varGamma ^{3/2}/35$, so that
 \begin{equation} F_{h}=\hat{V}_{0}\varLambda^{3/2}\int\limits_{0}^{\infty}rp(r)\,\mathrm{d}r, \end{equation}
\begin{equation} F_{h}=\hat{V}_{0}\varLambda^{3/2}\int\limits_{0}^{\infty}rp(r)\,\mathrm{d}r, \end{equation}where the scaled permeation velocity is defined as
The asymptotic solutions (3.3), (3.10) and (3.14) are, in rescaled form, respectively,
where ![]() $c^{*}={c}/{2{\rm \pi} }\approx 0.86$. The scaled equilibrium position,
$c^{*}={c}/{2{\rm \pi} }\approx 0.86$. The scaled equilibrium position, ![]() $\delta _{eq}$, is found by equating (4.1) with (2.10) and numerically solving for
$\delta _{eq}$, is found by equating (4.1) with (2.10) and numerically solving for ![]() $\delta$. Analytic expressions may be obtained at the limit of close approach, i.e. when
$\delta$. Analytic expressions may be obtained at the limit of close approach, i.e. when ![]() $\delta \ll 1$, in which (2.10) simplifies to
$\delta \ll 1$, in which (2.10) simplifies to ![]() $F_{s}\approx 7\delta ^{-5/4}$. Considering the limit
$F_{s}\approx 7\delta ^{-5/4}$. Considering the limit ![]() $\alpha \rightarrow 0$ simplifies (4.3) and (4.4), resulting in the following approximations:
$\alpha \rightarrow 0$ simplifies (4.3) and (4.4), resulting in the following approximations:
 \begin{gather}\delta_{eq}\approx\left(\frac{21}{4}\right)^{4/3}\varLambda^{{-}2/3}\hat{V}_{0}^{{-}4/3}, \quad\delta\ll 1,\ \varLambda\ll 1. \end{gather}
\begin{gather}\delta_{eq}\approx\left(\frac{21}{4}\right)^{4/3}\varLambda^{{-}2/3}\hat{V}_{0}^{{-}4/3}, \quad\delta\ll 1,\ \varLambda\ll 1. \end{gather} Figure 3(a) illustrates the dependence of each force on the distance from the membrane, ![]() $\delta$, at a scaled permeation velocity
$\delta$, at a scaled permeation velocity ![]() $\hat {V}_{0}=10^{-1}$, which is within the characteristic range of membrane separation (see table 1), and is chosen for a clear comparison between the competing forces. The hydrodynamic force is calculated numerically by (4.1) for various values of the brush permeance,
$\hat {V}_{0}=10^{-1}$, which is within the characteristic range of membrane separation (see table 1), and is chosen for a clear comparison between the competing forces. The hydrodynamic force is calculated numerically by (4.1) for various values of the brush permeance, ![]() $\varLambda$, with membrane permeance set as
$\varLambda$, with membrane permeance set as ![]() $\alpha \rightarrow 0$ and
$\alpha \rightarrow 0$ and ![]() $\alpha =10^{-3}$. The steric force,
$\alpha =10^{-3}$. The steric force, ![]() $F_{s}(\delta )$, is calculated explicitly from (2.10). Intersections of the curves for
$F_{s}(\delta )$, is calculated explicitly from (2.10). Intersections of the curves for ![]() $F_{s}$ and
$F_{s}$ and ![]() $F_{h}$ mark the equilibrium positions at each
$F_{h}$ mark the equilibrium positions at each ![]() $\varLambda$. Figure 3(a) demonstrates that the membrane permeance has little effect on the lubrication force for large
$\varLambda$. Figure 3(a) demonstrates that the membrane permeance has little effect on the lubrication force for large ![]() $\delta$. At close approach, however,
$\delta$. At close approach, however, ![]() $F_{h}$ tends to infinity for
$F_{h}$ tends to infinity for ![]() $\alpha \rightarrow 0$, while
$\alpha \rightarrow 0$, while ![]() $\alpha >0$ leads to a finite force as
$\alpha >0$ leads to a finite force as ![]() $\delta \rightarrow 0$, as expected. We note that here the hydrodynamic force increases with
$\delta \rightarrow 0$, as expected. We note that here the hydrodynamic force increases with ![]() $\varLambda$, as opposed to the trend in figure 2, due to the rescaling of
$\varLambda$, as opposed to the trend in figure 2, due to the rescaling of ![]() $F_{h}$ in (4.1), to enable an even comparison with
$F_{h}$ in (4.1), to enable an even comparison with ![]() $F_{s}$, while the results in figure 2 are scaled with the Stokes drag, in order to emphasise the increased drag due to the lubrication interaction. Physically, a decreased
$F_{s}$, while the results in figure 2 are scaled with the Stokes drag, in order to emphasise the increased drag due to the lubrication interaction. Physically, a decreased ![]() $\varLambda$ means the brush becomes denser and so
$\varLambda$ means the brush becomes denser and so ![]() $F_{h}$ increases. Within the parameter range shown in table 1, representing ‘real-world’ membrane separation, a brush permeance of
$F_{h}$ increases. Within the parameter range shown in table 1, representing ‘real-world’ membrane separation, a brush permeance of ![]() $\varLambda =O(10^{-3})$ results in
$\varLambda =O(10^{-3})$ results in ![]() $\delta _{eq}\approx 1$, at which point decreasing
$\delta _{eq}\approx 1$, at which point decreasing ![]() $\varLambda$ further will not improve the anti-fouling performance. Rather, it will decrease the combined membrane and brush permeance,
$\varLambda$ further will not improve the anti-fouling performance. Rather, it will decrease the combined membrane and brush permeance, ![]() $K=(k^{-1}+k_{p}^{-1})^{-1}$, which will then require a larger pressure
$K=(k^{-1}+k_{p}^{-1})^{-1}$, which will then require a larger pressure ![]() $p_0$ to maintain the same permeation velocity, resulting in increased energy consumption.
$p_0$ to maintain the same permeation velocity, resulting in increased energy consumption.

Figure 3. (a) The hydrodynamic (![]() $F_{h}$; solid and dotted-dashed curves for
$F_{h}$; solid and dotted-dashed curves for ![]() $\alpha \rightarrow 0$ and
$\alpha \rightarrow 0$ and ![]() $\alpha =10^{-3}$, respectively) and steric (
$\alpha =10^{-3}$, respectively) and steric (![]() $F_{s}$; dashed black curve) forces, evenly scaled, as functions of the scaled distance,
$F_{s}$; dashed black curve) forces, evenly scaled, as functions of the scaled distance, ![]() $\delta$, for various values of
$\delta$, for various values of ![]() $\varLambda$, the brush permeance. Here, the scaled permeation velocity is
$\varLambda$, the brush permeance. Here, the scaled permeation velocity is ![]() $\hat {V}_{0}=10^{-1}$.
$\hat {V}_{0}=10^{-1}$. ![]() $F_{h}$ is calculated numerically by (4.1), and
$F_{h}$ is calculated numerically by (4.1), and ![]() $F_{s}$ is given by (2.10). (b) Equilibrium position,
$F_{s}$ is given by (2.10). (b) Equilibrium position, ![]() $\delta _{eq}$, for which
$\delta _{eq}$, for which ![]() $F_{h}=F_{s}$, as a function of
$F_{h}=F_{s}$, as a function of ![]() $\hat {V}_{0}$ for varying
$\hat {V}_{0}$ for varying ![]() $\varLambda$. Solid and dashed lines denote
$\varLambda$. Solid and dashed lines denote ![]() $\alpha \rightarrow 0$ and
$\alpha \rightarrow 0$ and ![]() $\alpha =10^{-3}$, respectively, and the black dashed and dotted curves are the asymptotics for
$\alpha =10^{-3}$, respectively, and the black dashed and dotted curves are the asymptotics for ![]() $\delta \ll 1$,
$\delta \ll 1$, ![]() $\varLambda \gg 1$ and
$\varLambda \gg 1$ and ![]() $\varLambda \ll 1$, respectively. The shaded area marks the typical range of
$\varLambda \ll 1$, respectively. The shaded area marks the typical range of ![]() $\hat {V}_{0}$ for membrane separation (see table 1).
$\hat {V}_{0}$ for membrane separation (see table 1).
Table 1. Model parameters and characteristic values.

Figure 3(b) displays the equilibrium position of the particle, ![]() $\delta _{eq}$, found via the balance between the attractive and repulsive forces, as a function of the scaled velocity,
$\delta _{eq}$, found via the balance between the attractive and repulsive forces, as a function of the scaled velocity, ![]() $\hat {V}_{0}$, for representative values of
$\hat {V}_{0}$, for representative values of ![]() $\varLambda$, with
$\varLambda$, with ![]() $\alpha \rightarrow 0$ and
$\alpha \rightarrow 0$ and ![]() $\alpha =10^{-3}$. Naturally, an increase in
$\alpha =10^{-3}$. Naturally, an increase in ![]() $\hat {V}_{0}$ forces the particle closer to the membrane. A denser brush increases particle repulsion, resulting in a larger
$\hat {V}_{0}$ forces the particle closer to the membrane. A denser brush increases particle repulsion, resulting in a larger ![]() $\delta _{eq}$ for a given
$\delta _{eq}$ for a given ![]() $\hat {V}_{0}$. Neglecting the effect of membrane permeance (
$\hat {V}_{0}$. Neglecting the effect of membrane permeance (![]() $\alpha \rightarrow 0$), a decrease in
$\alpha \rightarrow 0$), a decrease in ![]() $\varLambda$ shifts the slope from
$\varLambda$ shifts the slope from ![]() $\delta _{eq}\propto \hat {V}_{0}^{-4}$ (
$\delta _{eq}\propto \hat {V}_{0}^{-4}$ (![]() $\varLambda \gg 1$) to
$\varLambda \gg 1$) to ![]() $\delta _{eq}\propto \hat {V}_{0}^{-4/3}$ (
$\delta _{eq}\propto \hat {V}_{0}^{-4/3}$ (![]() $\varLambda \ll 1$), corresponding to the shift from
$\varLambda \ll 1$), corresponding to the shift from ![]() $F_{h}\propto \delta ^{-1}$ (Brenner Reference Brenner1961) to
$F_{h}\propto \delta ^{-1}$ (Brenner Reference Brenner1961) to ![]() $F_{h}\propto \varLambda ^{-1}\delta ^{-1/2}$ (Fredrickson & Pincus Reference Fredrickson and Pincus1991), while increasing
$F_{h}\propto \varLambda ^{-1}\delta ^{-1/2}$ (Fredrickson & Pincus Reference Fredrickson and Pincus1991), while increasing ![]() $\alpha$ always tends to decrease
$\alpha$ always tends to decrease ![]() $F_{h}$, as discussed in § 3. Consequently, for a given
$F_{h}$, as discussed in § 3. Consequently, for a given ![]() $\hat {V}_{0}$, the
$\hat {V}_{0}$, the ![]() $\delta _{eq}$ curves for
$\delta _{eq}$ curves for ![]() $\alpha =10^{-3}$ lie above the corresponding ones for
$\alpha =10^{-3}$ lie above the corresponding ones for ![]() $\alpha \rightarrow 0$. While for
$\alpha \rightarrow 0$. While for ![]() $\varLambda \gtrsim 1$ the effect of
$\varLambda \gtrsim 1$ the effect of ![]() $\alpha \neq 0$ is seen only at small
$\alpha \neq 0$ is seen only at small ![]() $\delta _{eq}$, as the brush becomes denser the membrane permeance affects the equilibrium over a wider range. Physically, this is because thickening the brush enhances the resistance to the flow within the thin gap, and therefore the force extends over a longer distance. In the case
$\delta _{eq}$, as the brush becomes denser the membrane permeance affects the equilibrium over a wider range. Physically, this is because thickening the brush enhances the resistance to the flow within the thin gap, and therefore the force extends over a longer distance. In the case ![]() $\alpha >0$, the decrease in
$\alpha >0$, the decrease in ![]() $F_{h}$ then affects a wider range of
$F_{h}$ then affects a wider range of ![]() $\delta$.
$\delta$.
5. Concluding remarks
In this work we examined the effect of a polymer brush coating, applied to a membrane surface, on the hydrodynamic force, ![]() $F_{h}$, acting on a particle at close approach. Asymptotic solutions were derived, providing insight on trends in
$F_{h}$, acting on a particle at close approach. Asymptotic solutions were derived, providing insight on trends in ![]() $F_{h}$ as both the membrane and/or brush permeances,
$F_{h}$ as both the membrane and/or brush permeances, ![]() $\alpha$ and
$\alpha$ and ![]() $\varLambda$, respectively, are varied. Based on the balance between
$\varLambda$, respectively, are varied. Based on the balance between ![]() $F_{h}$ and the steric repulsion force, exerted by the brush as it is compressed by the particle, the equilibrium position of the particle,
$F_{h}$ and the steric repulsion force, exerted by the brush as it is compressed by the particle, the equilibrium position of the particle, ![]() $\delta _{eq}$, was calculated as a function of the scaled permeation velocity through the membrane,
$\delta _{eq}$, was calculated as a function of the scaled permeation velocity through the membrane, ![]() $\hat {V}_{0}$.
$\hat {V}_{0}$.
Equilibrium calculations illustrate the extent to which increasing ![]() $\hat {V}_{0}$ brings the particle closer to the membrane. The results also show that, beyond a certain brush density, one has
$\hat {V}_{0}$ brings the particle closer to the membrane. The results also show that, beyond a certain brush density, one has ![]() $\delta _{eq}\rightarrow 1$, whereby any further decrease to
$\delta _{eq}\rightarrow 1$, whereby any further decrease to ![]() $\varLambda$ will only increase the resistance to the flow and result in an increased energy input required to maintain the same permeation rate through the membrane. At close approach (
$\varLambda$ will only increase the resistance to the flow and result in an increased energy input required to maintain the same permeation rate through the membrane. At close approach (![]() $\delta _{eq}\ll 1$), analytic approximations were derived, showing the extent to which a dense brush (
$\delta _{eq}\ll 1$), analytic approximations were derived, showing the extent to which a dense brush (![]() $\varLambda \ll 1$) protects the surface compared with a dilute brush (
$\varLambda \ll 1$) protects the surface compared with a dilute brush (![]() $\varLambda \gg 1$) – trending as
$\varLambda \gg 1$) – trending as ![]() $\delta _{eq}\propto \hat {V}_{0}^{-4/3}$ and
$\delta _{eq}\propto \hat {V}_{0}^{-4/3}$ and ![]() $\hat {V}_{0}^{-4}$, respectively. Overall, these results provide insight into the capability of polymer brush coatings to prevent foulant particles from depositing on a membrane surface.
$\hat {V}_{0}^{-4}$, respectively. Overall, these results provide insight into the capability of polymer brush coatings to prevent foulant particles from depositing on a membrane surface.
Funding
The research was funded by grants from the Israel Science Foundation (2018/17) and the Israel Water Authority.
Declaration of interests
The authors report no conflict of interest.