2.1 Mean field approximation and the modulation equations

In this section, we shall introduce the mean field approximation that enables a straightforward derivation of the modulation system describing linear wave–mean flow interaction. The full justification of this approximation for the case of the interaction with a RW can be done in the framework of standard multiple-scale analysis (Luke Reference Luke1966), equivalent to single-phase modulation theory (Whitham Reference Whitham1999). The justification for linear wave–DSW interaction is more subtle, requiring the derivation of multiphase (two-phase) nonlinear modulation equations (Ablowitz & Benney Reference Ablowitz and Benney1970) and making linearisation in one of the oscillatory phases. To avoid unnecessary technicalities, we simply postulate the approximation used and then justify its validity by comparison of the obtained results with direct numerical simulations of the KdV equation.

To describe the interaction of a linear dispersive wave with an extended nonlinear dispersive–hydrodynamic state (RW or DSW), we represent the solution $u(x,t)$ of the KdV equation (1.7) as a superposition

where $u_{H.S.}(x,t)$ corresponds to the RW or DSW solution, and $\unicode[STIX]{x1D711}(x,t)$ corresponds to a small-amplitude field describing the linear wave.

In order to extract the dynamics of $\unicode[STIX]{x1D711}(x,t)$ , we make the mean field (scale separation) approximation by assuming that $u_{H.S.}(x,t)$ is locally (i.e. on the scale $\unicode[STIX]{x0394}x\sim \unicode[STIX]{x0394}t=O(1)$ ) periodic and replace the dispersive hydrodynamic wave field $u_{H.S.}(x,t)$ with its local mean (period average) value $\overline{u}(x,t)$ . Within this substitution, the small-amplitude approximation and the mean field assumption read

For a smooth, slowly varying hydrodynamic state (RW) such a replacement is natural since locally one has $u_{H.S.}=\overline{u}$ , but for the oscillatory solutions describing slowly modulated nonlinear wavetrains in a DSW, $u_{H.S.}(x,t)\neq \overline{u}$ so the mean field approximation would require justification via a careful multiple-scale analysis (Ablowitz & Benney Reference Ablowitz and Benney1970). In particular, a detailed analysis of possible resonances between the DSW and the wavepacket will be necessary (Dobrokhotov & Maslov Reference Dobrokhotov and Maslov1981). Such a mathematical justification will be the subject of a separate work, while here we shall postulate the outlined mean field approximation and show that it enables a remarkably accurate description of the linear field $\unicode[STIX]{x1D711}$ , which can be thought of as propagating on top of the mean flow.

Within the proposed mean field approximation, the small-amplitude wave field $\unicode[STIX]{x1D711}$ satisfies the linearised, variable coefficient KdV equation

where the mean flow $\overline{u}(x,t)$ evolves according to

For the case of linear wave–RW interaction, $V(\overline{u})=\overline{u}$ ; and the corresponding simplification of (2.4), known as the Hopf equation, is obtained by averaging the KdV equation over linear waves for which $\overline{u^{2}}=\overline{u}^{2}$ and $\overline{u_{xxx}}=0$ (El Reference El2005). For the linear wave–DSW interaction, $V(\overline{u})$ is given parametrically by (Gurevich & Pitaevskii Reference Gurevich and Pitaevskii1974)

where $K(m)$ and $E(m)$ are the complete elliptic integrals of the first and the second kind respectively (Abramowitz & Stegun Reference Abramowitz and Stegun1972), $m\in [0,1]$ , and $\overline{u}_{-}>\overline{u}_{+}$ are the values of $u$ at the left and right constant states respectively, connected by the DSW. The parameter $m$ is implicitly obtained as a self-similar solution with $V=x/t$ . Figure 2 displays the variation of the characteristic speed $V(\overline{u})$ and the mean flow $\overline{u}$ for $(\overline{u}_{-},\overline{u}_{+})=(1,0)$ . Equations (2.4), (2.5) follow from the Whitham modulation system obtained by averaging the KdV equation over the family of nonlinear periodic (cnoidal wave) KdV solutions (Whitham Reference Whitham1965b ). This system consists of three hyperbolic equations that can be diagonalised in Riemann invariant form. The DSW modulation is a simple wave (more specifically, a 2-wave (El & Hoefer Reference El and Hoefer2016)) solution of the Whitham equations, in which two of the Riemann invariants are set constant to provide continuous matching with the external constant states $u_{\pm }$ (Gurevich & Pitaevskii Reference Gurevich and Pitaevskii1974), see also Kamchatnov (Reference Kamchatnov2000). As we shall show, equations (2.3), (2.4), (2.5) provide an accurate description of the interaction between the linear wave and the DSW so that the dynamics of $\unicode[STIX]{x1D711}(x,t)$ is predominantly governed by the variations of the DSW mean value $\overline{u}(x,t)$ . We note that a similar mean flow approach, in which the oscillatory DSW field was replaced by its mean $\overline{u}$ has been recently successfully applied to the description of soliton–DSW interaction in Maiden et al. (Reference Maiden, Anderson, Franco, El and Hoefer2018).

Figure 2. (a) Variation of the characteristic speed of the Gurevich–Pitaevskii modulation (2.5) with $(\overline{u}_{-},\overline{u}_{+})=(1,0)$ . (b) Corresponding variation of the mean flow $\overline{u}(x/t)$ inside a DSW. The dashed lines correspond to the DSW edges.

Equations (2.3), (2.4) form our basic mathematical model for linear wave–mean flow interaction. We shall proceed by constructing modulation equations for this system. One may question the wisdom of incorporating the decoupled mean flow equation (2.4) to (2.3) rather than simply prescribing an arbitrary mean flow externally as has been done in previous works (Bretherton Reference Bretherton1968; Bretherton & Garrett Reference Bretherton and Garrett1968). As we will see, the mathematical structure of (2.3), (2.4) enables a convenient solution that is not available for generic mean flows $\overline{u}(x,t)$ . Moreover, equations (2.3), (2.4) transparently reveal the multi-scale structure of the dynamics: a fast equation (2.3) for the linear waves and a slow equation (2.4) for the mean flow.

Let $\unicode[STIX]{x1D711}(x,t)$ describe a slowly varying wavepacket,

where

These are standard assumptions in modulation theory (Whitham Reference Whitham1965b , Reference Whitham1999), that can be conveniently formalised by introducing slow space and time variables $X=\unicode[STIX]{x1D700}t$ , $T=\unicode[STIX]{x1D700}t$ , where $\unicode[STIX]{x1D700}\ll 1$ is a small parameter, and assuming that $a=a(X,T)$ , $k=k(X,T)$ , $\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}(X,T)$ . To describe the interaction of a linear wavepacket with a nonlinear hydrodynamic state, we require that the slow variations of the linear wave’s parameters and the variations of the mean flow occur on the same spatio-temporal scale, i.e. $\overline{u}=\overline{u}(X,T)$ . Substituting (2.6) in (2.2), we reduce the scale separation conditions between the linear wave and the mean flow to

Conditions  (2.7) and (2.8) are the main assumptions underlying the modulation theory of linear wave–mean flow interaction described here.

The derivation of modulation equations for $a$ and $k$ is then straightforward using Whitham’s variational approach (cf. for instance Whitham Reference Whitham1999, Ch. 11), and yields (1.1) with

We also derive a useful consequence of the wave conservation law (cf. (1.1a )) for a wavepacket train consisting of a superposition of two slowly modulated plane waves with close wavenumbers $k$ and $k+\unicode[STIX]{x1D6FF}k$ where $\unicode[STIX]{x1D6FF}k\ll k$ , which corresponds to beating of the two waves. The conservation of waves for these two waves reads

Hence, for $\unicode[STIX]{x1D6FF}k\ll k$ , the subtraction of these two equations reduces to a conservation equation for $\unicode[STIX]{x1D6FF}k$ that is very similar to the conservation of wave action

Concluding this section, we note that the modulation system (1.1), (2.9) is quite simple and definitively not new. However, unlike in previous studies, it is now coupled to the mean field equation (2.4). As we shall show, the system consisting of (1.1), (2.4), (2.9) and (2.11) equipped with appropriate initial conditions, yields straightforward yet highly non-trivial implications, especially in the case of wavepacket–DSW interaction, which is very difficult to tackle using direct (non-modulation) analysis.

2.2 Riemann invariants

In what follows, we shall use an abstract field $A(x,t)$ representing either ${\mathcal{A}}(x,t)=a(x,t)^{2}/k(x,t)$ or $\unicode[STIX]{x1D6FF}k(x,t)$ such that the reduced modulation system composed of (1.1), (2.4), (2.9) and (2.11) can be cast in the general form

where $v_{g}(k,\overline{u})=\unicode[STIX]{x2202}_{k}\unicode[STIX]{x1D714}=\overline{u}-3k^{2}$ , $\unicode[STIX]{x2202}_{\overline{u}}\unicode[STIX]{x1D714}=k$ and $V(\overline{u})=\overline{u}$ or that given in (2.5). We note that the system (2.12) has the double characteristic velocity $v_{g}$ and thus is not strictly hyperbolic. In fact, there are only two linearly independent characteristic eigenvectors associated with the modulation system (2.12), so this system of three equations is only weakly hyperbolic. The first two equations, (2.12a ) and (2.12b ), are decoupled and can always be diagonalised such that (2.12b ) takes the form

for the Riemann invariant $q=Q(k,\overline{u})$ . Generally, the Riemann invariant $q$ as a function of $\overline{u}$ and $k$ is found by integrating the characteristic differential form

For the case of linear wave–RW interaction, we have $V(\overline{u})=\overline{u}$ , so $\unicode[STIX]{x1D6EF}=-3k^{2}\,\text{d}k+k\,\text{d}\overline{u}$ which can be integrated after multiplying by the integrating factor $1/k$ to yield explicit expressions for the Riemann invariant $q$ and the associated characteristic velocity

It follows from (2.13) that $q=\text{const}\equiv q_{0}$ along the double characteristic $\text{d}x/\text{d}t=v_{g}$ , which enables one to manipulate (2.12c ) into the form

valid along $\text{d}x/\text{d}t=v_{g}$ , where

with $\overline{u}_{0}$ a constant of integration. The quantity $pA$ thus can be viewed as a Riemann invariant of the system (2.12) on the integral surface $Q(k,\overline{u})=q_{0}$ which will prove useful in the analysis that follows. We stress, however, that $pA$ is not a Riemann invariant in the conventional sense since the system (2.12) does not have a full set of characteristic eigenvectors. See Maiden et al. (Reference Maiden, Anderson, Franco, El and Hoefer2018) for a similar construction in the context of soliton–mean flow interaction.

For $V(\overline{u})=\overline{u}$ , the integral in (2.17) is readily evaluated to give, taking into account (2.15),

Note, that the described diagonalisation of the reduced modulation system (2.12) for the linear wave–mean flow interaction, unlike the existence of Riemann invariants of the general Whitham system for modulated cnoidal waves (Whitham Reference Whitham1965b ), does not rely on integrability of the KdV equation. In fact, the possibility of this diagonalisation is general and is a direct consequence of the absence of an induced mean flow for linearised waves, so that the dynamics of the wave parameters $(k,\unicode[STIX]{x1D714},a)$ is decoupled from the dynamics of the mean flow $\overline{u}$ . Here, we reap the benefits of jointly considering the evolution of the mean flow, wavenumber conservation and the field equation in (2.12) by recognising that they can be cast in diagonal, Riemann invariant form (2.12a ), (2.13) and (2.16) along $Q(k,\overline{u})=q_{0}$ .

3.1 Adiabatic invariants and transmission conditions

Before studying the interaction of localised wavepackets with a mean flow in the framework of the basic system (2.3), (2.4), we consider a model problem of the unidirectional scattering of a linear plane wave (PW) by a nonlinear hydrodynamic state (RW or DSW) initiated by a step in $\overline{u}$ . We denote the incident PW parameters at $x\rightarrow +\infty$ as $k_{+},a_{+}$ and the transmitted PW parameters at $x\rightarrow -\infty$ as $k_{-},a_{-}$ . To find the transmission relations, we consider the generalised Riemann problem (see figure 3)

We call this Riemann problem generalised as it is formulated for the modulation system (2.12) rather than for the original dispersive model (2.3), (2.4).

Figure 3. Schematic of the initial conditions for the interaction between a plane wave and a hydrodynamic state.

In the interaction of a PW with both a RW and a DSW, the evolution of $\overline{u}(x,t)$ is described by the self-similar expansion fan solution of the mean flow equation (2.12a )

while the Riemann invariants $q$ and $pA$ are constant throughout, implying the relations

where $A_{\pm }=a_{\pm }^{2}/k_{\pm }$ . These conserved quantities generalise the conservation of wave frequency and wave action, equation (1.2), for steady mean flows to the unsteady case. The expressions for $Q(k,\overline{u})$ and $P(k,\overline{u})$ in the PW–RW interactions for KdV are given by (2.15) and (2.18), respectively. For PW–DSW interaction, when $V(\overline{u})$ is given by (2.5), simple explicit expressions for $Q$ and $P$ in terms of $k$ and $\overline{u}$ are not available. However, they can be obtained by integrating (2.14) and evaluating (2.17), e.g. numerically. The edge speeds of the expansion fan (3.2) are given by

Expressions (3.6) follow from (2.5) upon taking $m\rightarrow 0^{+}$ and $m\rightarrow 1^{-}$ for the trailing and the leading DSW edge respectively, see Gurevich & Pitaevskii (Reference Gurevich and Pitaevskii1974).

Given $\overline{u}(x,t)$ described by (3.2), the conservation of $q$ and $pA$ in (3.3), (3.4) yields not only the PW transmission relations but also the slow variations of the PW parameters $k(x/t)$ and $a(x/t)$ due to the interaction with the mean flow in the hydrodynamic state. Constant $q$ and $pA$ can thus be seen as adiabatic invariants of the PW–mean flow interaction.

The conservation relations (3.3), (3.4) also describe wave–mean flow interaction for a system of two beating, superposed slowly modulated plane waves with close wavenumbers $k$ and $k+\unicode[STIX]{x1D6FF}k$ interacting with a RW (cf. § 2.1). In this case, the adiabatic variation of $k$ and $\unicode[STIX]{x1D6FF}k$ are described respectively by (3.3) and (3.4) where $A$ corresponds now to $\unicode[STIX]{x1D6FF}k$ .

As we already mentioned, relations (3.2), (3.3) and (3.4) are valid for both PW–RW ( $\overline{u}_{-}<\overline{u}_{+}$ ) and PW–DSW ( $\overline{u}_{-}>\overline{u}_{+}$ ) interactions. We now consider these two cases in more detail.

3.2 Plane wave–rarefaction wave interaction

A RW is generated when $\overline{u}_{-}<\overline{u}_{+}$ , and the resulting mean flow variation is described by (3.2) with characteristic velocity $V(\overline{u})=\overline{u}$ . In this case, explicit expressions for the adiabatic invariants $q$ and $pA$ can be obtained using (2.15) and (2.18). The conservation relations (3.3), (3.4) then yield

where the second condition was obtained by using $A_{\pm }=a_{\pm }^{2}/k_{\pm }$ . It is surprising that the interaction of a PW with a non-uniform, unsteady hydrodynamic state does not change the PW amplitude, which is in sharp contrast with the classical case of the interaction of a surface water wave with a counter-propagating steady current where the amplitude varies following the inhomogeneities of the current in (1.2). In this latter case, the wave amplitude can become extremely large during the interaction with the mean flow (and hence the wave is no longer described by linear theory) while (3.8) describing dynamic wave–mean flow interaction ensures that the PW remains a small-amplitude linear wave regardless of its wavenumber. In particular no wave breaking occurs during the interaction with a RW.

Figure 4. Hydrodynamic reciprocity of plane wave–RW and plane wave–DSW interactions: conservation of $Q(k,\overline{u})$ and $a$ in (3.7) and (3.8). (a) Modulated plane wave $\unicode[STIX]{x1D711}=a\cos \unicode[STIX]{x1D703}$ , $\unicode[STIX]{x1D703}_{x}=k$ , $\unicode[STIX]{x1D703}_{t}=-\unicode[STIX]{x1D714}(k,\overline{u})$ , outside of the domain of interaction with the hydrodynamic state, where $\overline{u}_{-}>\overline{u}_{+}$ , describing PW–DSW interaction for $t>0$ and PW–RW interaction for $t<0$ . (b) The relationship between the dominant wavenumbers of incident and transmitted wavepackets with $a_{0}=0.01$ . The solid line corresponds to the analytical relation (3.7) when $(\overline{u}_{-},\overline{u}_{+})=(1,0)$ . The crosses (+) and circles (○) are identified with PW–RW and PW–DSW interaction, respectively. The relation between $k_{-}$ and $k_{+}$ is independent of the nature of the hydrodynamic state.

Figure 4 displays the comparison between the relation (3.7) and the wavenumbers obtained in numerical simulations of linear wave–mean flow interaction. In numerical simulations, we employed the more adequate partial Riemann problem defined in § 4.1 for which we will show that the relation (3.7) remains valid. One can see that (3.7) yields the transmission condition: the transmitted PW exists if its wavenumber $k_{-}$ is a real number. This requirement reduces to the following condition for transmission of the incident PW with wavenumber $k_{+}$ as

The case $k_{+}<k_{c}$ will receive further interpretation in § 4 in the context of the interaction of a localised wavepacket with a RW as wave trapping inside the hydrodynamic state.

One can also consider the interaction between two beating superposed PWs and a RW (see the discussion in § 2.1) where the conservation of the adiabatic invariant $p(k,\overline{u})A$ with $A=\unicode[STIX]{x1D6FF}k$ yields

As was mentioned in the previous section, the beating pattern created by the superposition of two PWs with close wavenumbers ( $\unicode[STIX]{x1D6FF}k\ll k$ ) can be seen as a wavepacket train of period $L=4\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FF}k$ . Thus (3.10) provides the relation between the wavelength of the incident train $L_{+}$ and the transmitted train $L_{-}$ . The difference

can be interpreted as the phase shift between the incident and the transmitted wavepackets. Similarly, one can interpret $L_{\pm }$ as the widths of the wavepackets before and after transmission. Their relation is then given by

3.3 Plane wave–dispersive shock wave interaction: hydrodynamic reciprocity

We now consider the initial condition (3.1) with $\overline{u}_{-}>\overline{u}_{+}$ that resolves into a DSW. In this case, the modulation of the mean flow is described by the simple wave equation (2.5), (3.2) and the expressions for the adiabatic invariants $q$ and $pA$ differ from (2.15), (2.18) obtained for PW–RW interaction. As a result, the conditions (3.3), (3.4) for the conservation of $q$ and $pA$ describe a very different adiabatic evolution of the PW parameters inside the dispersive hydrodynamic state. We shall consider this evolution later in § 4.4, while here we describe a very general property of PW interaction with dispersive hydrodynamic states termed hydrodynamic reciprocity, that was initially formulated in Maiden et al. (Reference Maiden, Anderson, Franco, El and Hoefer2018) for mean field interaction of solitons with dispersive hydrodynamic states.

When $\overline{u}_{-}>\overline{u}_{+}$ , we observe that the PW–DSW and PW–RW interactions in the mean flow approximation are described by the solutions of the same Riemann problem considered for the $t>0$ and $t<0$ half-planes, respectively. Then, continuity of the simple wave modulation solution for all $(x,t)$ (illustrated by figure 4 a), except at the origin $(x,t)=(0,0)$ , implies that the transition relations (3.7) and (3.8) derived for the PW–RW interaction ( $t<0$ ) must also hold for $t>0$ , i.e. for the PW–DSW interaction. This hydrodynamic reciprocity is verified in figure 4(b), where we compare the relations between $k_{-}$ and $k_{+}$ obtained numerically for the evolution of PW–RW and PW–DSW interactions in the full KdV equation. The agreement confirms that relation (3.7), as well as the transmission condition (3.9), indeed hold for PW interaction with both nonlinear dispersive hydrodynamic states: RW and DSW.

The agreement between relation (3.7) and the numerical solution of the Riemann problem in figure 4 also confirms the mean field hypothesis underlying the basic mathematical model (2.3) of this paper. Although the mean field assumption is arguably intuitive for PW–RW interaction where the hydrodynamic state solution $u_{H.S.}$ , up to small dispersive corrections at the RW corners, coincides with the solution of (2.4) for mean flow evolution $\overline{u}=V(\overline{u})$ , it is no longer so for the highly non-trivial PW–DSW interaction where $u_{H.S.}$ describes a rapidly oscillating structure, which is radically different from its slowly varying mean flow $\overline{u}$ satisfying the equations (2.4), (2.5).

The relative difference between the numerically observed wavenumber $k_{-}^{num}$ and the predicted wavenumber $k_{-}$ for transmitted wavepackets through RWs and DSWs is shown in figure 5. While the relative error in the small-amplitude regime reported in figure 4 is of the order of $10^{-3}$ , it is surprising that the wavenumber prediction from linear theory holds equally as well for wavepackets with order-one amplitudes.

Figure 5. Relative error $k_{-}^{num}/k_{-}-1$ where $k_{-}^{num}$ is obtained numerically and $k_{-}$ satisfies (3.7) with $k_{+}=0.88$ and $(\overline{u}_{-},\overline{u}_{+})=(0,1)$ (PW–RW) or $(\overline{u}_{-},\overline{u}_{+})=(1,0)$ (PW–DSW). The numerical results are obtained for different amplitudes $a_{0}$ of the incident wavepacket. The crosses (+) and circles (○) correspond to the interaction with a RW and DSW, respectively.

4.1 Partial Riemann problem

Having considered the model case of PW interaction with dispersive hydrodynamic states, we now proceed with a more physically relevant example of a similar interaction involving localised linear wavepackets instead of PWs. To model such an interaction, the Riemann problem (2.12), (3.1) must be modified to take into account the localised nature of the wavepacket. To this end, we introduce the partial Riemann problem

where the amplitude profile is localised and centred at $x=X_{0}$ . We take a Gaussian $f(y)=\text{e}^{-y^{2}/L_{0}^{2}}$ with width $L_{0}$ . In what follows, the position of the wavepacket, defined as a group velocity line, is denoted by $X(t)$ , so that according to (4.1), $X(0)=X_{0}$ . While the wavepacket is localised, we consider a sufficiently broad initial amplitude distribution that does not vary significantly over one period $2\unicode[STIX]{x03C0}/k$ of the oscillation of the carrier wave, $L_{0}\gg 2\unicode[STIX]{x03C0}/k_{\pm }$ , such that the amplitude modulation is well described by (2.12c ), see conditions (2.7). We also require $|X_{0}|\gg L_{0}$ so that the initial wavepacket is well separated from the initial step in the mean flow at the origin.

The quantities $k_{+}$ and $k_{-}$ here denote the dominant wavenumbers of the wavepackets for $x>0$ and $x<0$ respectively. Note that, although the wavepacket dominant wavenumber is defined only along the group velocity line, we treat it here as a spatio-temporal field $k(x,t)$ , and the formulation (4.1a ) assumes the simultaneous presence of two wavepackets at $t=0$ with dominant wavenumbers $k_{-}$ and $k_{+}$ . Still only one of them – we shall call it the incident wavepacket – is physically realised due to the localised nature of the amplitude distribution. The additional, fictitious wavepacket yields all the transmission, trapping information of the incident wavepacket. See Maiden et al. (Reference Maiden, Anderson, Franco, El and Hoefer2018) for a similar extension made to define a soliton amplitude field in the context of the soliton–mean flow interaction problem.

The partial Riemann problem (2.12), (4.1) implies two possible interaction scenarios: (i) a right-incident interaction where a wavepacket, initially placed at $X_{0}>0$ , propagates with group velocity $v_{g}^{+}=\overline{u}_{+}-3k_{+}^{2}$ and enters either an expanding hydrodynamic structure whose leading edge velocity is $V(\overline{u}_{+})>v_{g}^{+}$ (see (3.5), (3.6)); (ii) a left-incident interaction, where the wavepacket is initially placed at $X_{0}<0$ so that the interaction only occurs if $V(\overline{u}_{-})<v_{g}^{-}=\overline{u}_{-}-3k_{-}^{2}$ . It follows from (3.5), (3.6) that this can happen only for a DSW but not for a RW.

The subsystem (2.12a ), (2.12b ) and (4.1a ) for $\overline{u}$ and $k$ has already been solved in the previous section. The simple wave solution of this problem is given by (3.2) and (3.3), and thus the relation between $k_{-}$ and $k_{+}$ (3.7) obtained for PWs, holds for the wavepacket–mean flow interaction. As a consequence, the wavepacket is subject to the transmission condition (3.9). The possible interaction configurations are summarised in table 1. The partial Riemann problem (1.7), (4.1) was solved numerically to verify the relation (3.7) in figure 4. Its numerical implementation is detailed in appendix A.

4.2 Conservation of the integral of wave action

We now proceed with the determination of the wavepacket amplitude variation resulting from the interaction with dispersive hydrodynamic states. It is well known that KdV dispersion leads to wavepacket broadening so that the amplitude $a(x,t)$ decreases during propagation on a constant mean flow $\overline{u}_{-}$ or $\overline{u}_{+}$ in order to conserve the integral $\int _{-\infty }^{\infty }a^{2}\,\text{d}x$ , which leads to the standard dispersive decay estimate $a\sim t^{-1/2}$ for $t\gg 1$ (Whitham Reference Whitham1999). Thus, we cannot expect the amplitude transmission relation (3.8) derived for PWs to remain valid for localised wavepackets. To address this issue, instead of considering the amplitude of the wave, we consider the integral of wave action

between two group lines $\text{d}X_{1,2}/\text{d}t=v_{g}(k(x,t),\overline{u}(x,t))|_{x=X_{1,2}(t)}$ . It then follows from (1.1b ) and (2.9b ) that the integral (4.2) is conserved during linear wavepacket propagation through a hydrodynamic state with varying mean flow $\overline{u}(x,t)$ (Whitham Reference Whitham1965a ; Bretherton & Garrett Reference Bretherton and Garrett1968).

If the incident wavepacket is transmitted and remains localised, we can evaluate the integral (4.2) before $(t<t_{+})$ and after ( $t>t_{-}$ ) the interaction when the wave is localised at the right or the left of the hydrodynamic state, respectively, and where the wavenumber field is uniform $k(x,t)=k_{+}$ for $t<t_{+}$ or $k(x,t)=k_{-}$ for $t>t_{-}$ where $a(x,t)\neq 0$ . Thus, the conservation of the integral of wave action $E(t_{-})=E(t_{+})$ yields

where we replace the limits of integration $X_{1}$ and $X_{2}$ by $-\infty$ and $+\infty$ since the wavepacket is localised in space. The relation (4.3) is valid in both linear wavepacket-RW and -DSW interactions, as illustrated in figure 6. Similar to the relation between $k_{-}$ and $k_{+}$  (3.7), equation (4.3) holds beyond the small-amplitude limit of the wavepacket as displayed by the right plot in figure 6.

In the case of a broad wavepacket of almost constant amplitude, we have the following approximation:

where $a_{\pm }$ and $L_{\pm }$ are, respectively, the constant amplitude and width of the wavepacket before and after interaction with a hydrodynamic state. It follows from the wave conservation law that the widths $L_{\pm }$ of the wavepackets on both sides of the hydrodynamic state satisfy $L_{-}/k_{-}=L_{+}/k_{+}$ (see (3.12)) so that (4.3) and (4.4) yield the approximate conservation of amplitude $a_{-}\approx a_{+}$ , which agrees with (3.8) obtained for the limiting case of PW–mean flow interaction.

Figure 6. (a) Comparison between the integral of wave action computed before ( $t=t_{+}$ ), and after ( $t=t_{-}$ ), the transmission of the wavepacket: $E_{\pm }=(\int _{-\infty }^{+\infty }a(x,t_{\pm })^{2}\,\text{d}x)/k_{\pm }$ for the Riemann problem depicted in figure 4. The solid line (——) corresponds to (4.3) and the crosses (+) or circles (○) are obtained numerically from linear wavepacket-RW or -DSW interaction, respectively with $a_{0}=0.01$ and variable $k_{+}$ . (b) Relative error $E_{-}/E_{+}-1$ for $k_{+}=0.88$ and different amplitudes $a_{0}$ of the initial wavepacket.

4.3 Wavepacket–rarefaction wave interaction

In this section, we consider in detail the interaction between a wavepacket and a RW; as we already mentioned, the linear wavepacket interacts with the RW only if initially $x=X_{0}>0$ (see table 1). The fields $\overline{u}$ and $k$ are the solution of the Riemann problem studied in § 3.2. The variation of $\overline{u}(x,t)$ is described by the relation (3.2) with $V(\overline{u})=\overline{u}$ , and the variation of $k(x,t)$ is given by

obtained through the conservation of the adiabatic invariant (2.15). The identification of a dominant wavenumber when the wavepacket propagates inside the hydrodynamic state implies that $k(x,t)$ , or similarly $\overline{u}(x,t)$ , is almost constant across the wavepacket. This latter condition is readily satisfied for sufficiently large $t$ as the RW mean flow satisfies $\overline{u}_{x}=1/t$ .

Since the wavepacket propagates with the group velocity $v_{g}(k,\overline{u})=\overline{u}-3k^{2}$ , its position $X(t)$ satisfies the characteristic equation

The integration of (4.6) yields

where $t_{+}=X_{0}/(3k_{+}^{2})$ and $t_{-}=X_{0}/(3k_{+}k_{-})$ . Hence, during the interaction with the RW, the temporal variation of the dominant wavepacket wavenumber $K(t)$ along the group velocity line is given by

The wavepacket trajectory described by (4.7) is compared with the numerically observed trajectory in figure 7 for two different configurations: transmission ( $k_{+}>k_{c}$ , cf. (3.9)) and trapping ( $k_{+}<k_{c}$ ). Snapshots of the envelope $a(x,t)$ of the wavepacket field $\unicode[STIX]{x1D711}(x,t)$ and the absolute value of its Fourier transform $|\tilde{\unicode[STIX]{x1D711}}(k,t)|$ are presented in figure 8. The numerical procedure implemented to extract $\unicode[STIX]{x1D711}(x,t)$ from the full numerical solution of (1.7) is explained in appendix A.

In figure 8, the wavepacket shape in Fourier space slightly deviates from Gaussian when it enters the leading RW edge at $t=500$ . However, the wavepacket recovers its Gaussian form when it is fully inside the RW and after exiting the RW.

Figure 7. (a) Trajectories of wavepacket–RW interaction. Solid lines correspond to the solution (4.7) and markers to the numerical trajectory. The triangles (▴▴) correspond to the transmission configuration for $k_{+}=1$ and the dots ( $\bullet \bullet$ ) correspond to the trapping configuration when $k_{+}=0.7$ . The RW edges $x=\overline{u}_{\pm }t$ are represented by dotted lines (- - -). (b) The corresponding temporal variation of the wavepacket wavenumber. Solid lines correspond to the solution (4.8) and markers to the numerical result.

Figure 8. Numerical evolution of wavepacket–RW interaction in the case of transmission (a) and trapping (b). The first column displays the extracted wavepacket envelope $a(x,t)$ . The positions of the RW edges are shown by dotted lines (- - -). The second column displays the amplitude of the wavepacket’s Fourier transform, denoted $\tilde{\unicode[STIX]{x1D711}}$ .

While the wavepacket propagates at constant velocity over a non-modulated mean flow $\overline{u}(x,t)=\overline{u}_{+}$ or $\overline{u}(x,t)=\overline{u}_{-}$ , the wavepacket decelerates during the propagation inside the RW for $t_{+}<t<t_{-}$ . Note that acceleration/deceleration here is understood as the increasing/decreasing of the group speed $|v_{g}(X,t)|$ . If the transmission condition (3.9) is not satisfied, $\lim _{t\rightarrow \infty }K(t)=0$ , and the incident wavepacket gets trapped inside the RW as its velocity $v_{g}=\overline{u}-3K^{2}$ converges asymptotically to the local background velocity $\overline{u}$ . Moreover, the wavepacket amplitude decays indefinitely, following the conservation of wave action (4.2), and the wavepacket eventually gets absorbed by the RW (see figure 8 b).

We now draw certain parallels between the trapping of linear waves in RWs and the effect of so-called wave blocking in counter-propagating, inhomogeneous steady currents $U(x)<0$ , where the wavenumber $k(x)$ also varies following the inhomogeneities of the current (recall the discussion in § 1). In this case, the adiabatic variation of the wavenumber is simply described by the conservation of the frequency $\unicode[STIX]{x1D714}(k(x);U(x))=\text{const}$ . In contrast to wave trapping due to wavepacket–RW interaction considered here, wave blocking in the counter-propagating current is accompanied by a decrease in wavepacket wavelength and an increase in amplitude, until it reaches the stopping velocity $v_{g}=0$ at some finite wavenumber.

The trajectory of the wavepacket displayed in figure 7(a) shows that the wavepacket undergoes refraction due to its interaction with the RW. In the transmission configuration, this results in both a speed shift and a phase shift of the transmitted wavepacket. The phase of the wave after its transmission is equal to $X_{-}=3k_{-}^{2}t_{-}\neq X_{0}$ (cf. (4.7) for $t>t_{-}$ ), so that the phase shift $\unicode[STIX]{x1D6E5}_{-}=X_{-}-X_{0}$ is

This result can also be obtained from the second adiabatic invariant $pA$ in (3.4) where $A=\unicode[STIX]{x1D6FF}k$ as in (3.10). Viewing the wavepacket as part of a fictitious periodic train of wavepackets, we recognise that the relative position of the wavepackets post ( $x=X_{-}$ ) and pre ( $x=X_{0}$ ) interaction is inverse to the relative beating wavenumber shift $X_{-}/X_{0}=\unicode[STIX]{x1D6FF}k_{+}/\unicode[STIX]{x1D6FF}k_{-}=k_{-}/k_{+}$ . Since $k_{-}<k_{+}$ , the phase shift is negative in the considered situation. The formula (4.9) is precisely (3.11) when we identify $L_{+}$ with $X_{0}$ , using the second adiabatic invariant $p\unicode[STIX]{x1D6FF}k$ . Figure 9(a) displays the phase shift computed numerically for different wavenumbers $k_{+}$ , which agrees with relation (4.9). In addition, the relation (4.9) holds for large-amplitude wavepackets, just as the relations (3.7) and (4.3) do.

Figure 9. Numerical determination of the normalised phase shift $\unicode[STIX]{x1D6E5}_{-}/X_{0}$ for wavepacket–RW interaction (a) and wavepacket–DSW interaction (b). In the two plots, the markers (pluses + for the RW interaction and circles ○ for the DSW interaction) correspond to the numerical simulation and the solid line to the analytical prediction (4.9). The inset plots correspond to the relative error $\unicode[STIX]{x1D6E5}_{-}^{num.}/\unicode[STIX]{x1D6E5}_{-}-1$ between $\unicode[STIX]{x1D6E5}_{-}^{num.}$ determined numerically and $\unicode[STIX]{x1D6E5}_{-}$ given by the relation (4.9).  $\unicode[STIX]{x1D6E5}_{-}^{num.}$ is obtained for different initial wavepacket amplitudes $a_{0}$ , $k_{+}=1.2$ for wavepacket–RW interaction (+) and $k_{+}=0.88$ for wavepacket–DSW interaction (○).

4.4 Wavepacket–DSW interaction

We now consider the more complex case of wavepacket–DSW interaction. Such an interaction is generally described by two-phase KdV modulation theory, which is quite technical, with modulation equations given in terms of hyperelliptic integrals (Flaschka, Forest & McLaughlin Reference Flaschka, Forest and McLaughlin1980). The mean field approach adopted here enables us to circumvent these technicalities by employing the approximate modulation system (2.12) that yields simple and transparent analytic results that, as we will show, agree extremely well with direct numerical simulations. More broadly, the notion of hydrodynamic reciprocity described in § 3.3 can be utilised without approximation to make specific predictions for wavepacket–DSW interaction for $t>0$ based on wavepacket–RW interaction for $t<0$ .

As already mentioned, wavepacket–DSW interaction admits two basic configurations (see table 1): the transmission configuration, arising when $X_{0}>0$ and applicable to any incident wavenumber $k_{+}>0$ , and the trapping configuration, when $X_{0}<0$ and the incident wavenumber $k_{-}>0$ is sufficiently small. The variation of $\overline{u}(x,t)$ inside the DSW is given by $\overline{u}=V^{-1}(x/t)$ (see (3.2)) where the characteristic velocity $V(\overline{u})$ is defined by (2.5).

The variation of the wavepacket’s wavenumber field $k(x,t)$ is given by the adiabatic invariant $q$ , which can be obtained by integrating the differential form $\unicode[STIX]{x1D6EF}$ in (2.14). This differential form vanishes on the group velocity characteristic $\text{d}x/\text{d}t=v_{g}$ , yielding a relation between $k$ and $\overline{u}$ specified by the ordinary differential equation (ODE)

with the boundary condition $k(\overline{u}_{+})=k_{+}$ if $X_{0}>0$ or $k(\overline{u}_{-})=k_{-}$ if $X_{0}<0$ . Note that (4.10) for $V(\overline{u})=\overline{u}$ arises in the DSW fitting method where it determines the locus of the KdV DSW harmonic edge, see El (Reference El2005), El & Hoefer (Reference El and Hoefer2016). Here, it has a different meaning and does not appear to be amenable to analytical solution because of the presence of elliptic integrals in the function $V(\overline{u})$ . We therefore solve (4.10) numerically. Once the relation $k(\overline{u})$ has been determined, the $(x,t)$ -dependence of the wavenumber inside the DSW is $k=k(\overline{u}(x,t))=k(V^{-1}(x/t))$ . The wavepacket trajectory in the $(x,t)$ -plane is obtained by solving (4.6) with the already determined $\overline{u}(x,t)$ and $k(x,t)$ . The results of our semi-analytical computations are presented in figures 10 and 11.

Figure 10. (a) Wave curves for wavepacket–DSW interaction obtained by numerical integration of (4.10) with $(\overline{u}_{-},\overline{u}_{+})=(1,0)$ . Solid curves (——) correspond to transmission configurations ( $k(\overline{u}_{-})>\sqrt{2/3}$ ), dashed curves (– –) to trapped configurations ( $k(\overline{u}_{-})<\sqrt{2/3}$ ) and the dash-dotted curve (— -) to the limiting case $k(\overline{u}_{-})\simeq \sqrt{2/3}$ . The arrows correspond to the direction associated with propagation of the wavepacket. (b) Deviation of the predicted transmitted wavenumber $k(\overline{u}_{-})$ from the actual value $k_{-}$ obtained from (3.7) and hydrodynamic reciprocity, as a function of $k_{-}$ with $\overline{u}_{-}=1$ , $\overline{u}_{+}=0$ . The vertical dash-dotted line is the minimum transmitted wavenumber $k_{-}=\sqrt{2/3}$ .

Figure 10(a) displays the wave curves $k(\overline{u})$ obtained from the numerical integration of (4.10), that can be interpreted as wavepacket trajectories in the parameter space $(\overline{u},k)$ . The evolution of the wavepacket’s wavenumber $K(t)=k(\overline{u}(X/t))$ along a wave curve is then described by an ODE

obtained by combining $\overline{u}=V^{-1}(X/t)$ , equations (4.6) and (4.10). Since the characteristic speed $V(\overline{u})$  (2.4) of the Gurevich–Pitaevskii modulation equation is a decreasing function of $\overline{u}$ (cf. figure 2), equation (4.11) shows that the wavepacket’s wavenumber is increasing during its propagation inside the DSW, in contrast to wavepacket–RW interaction for which $V^{\prime }(\overline{u})=1>0$ .

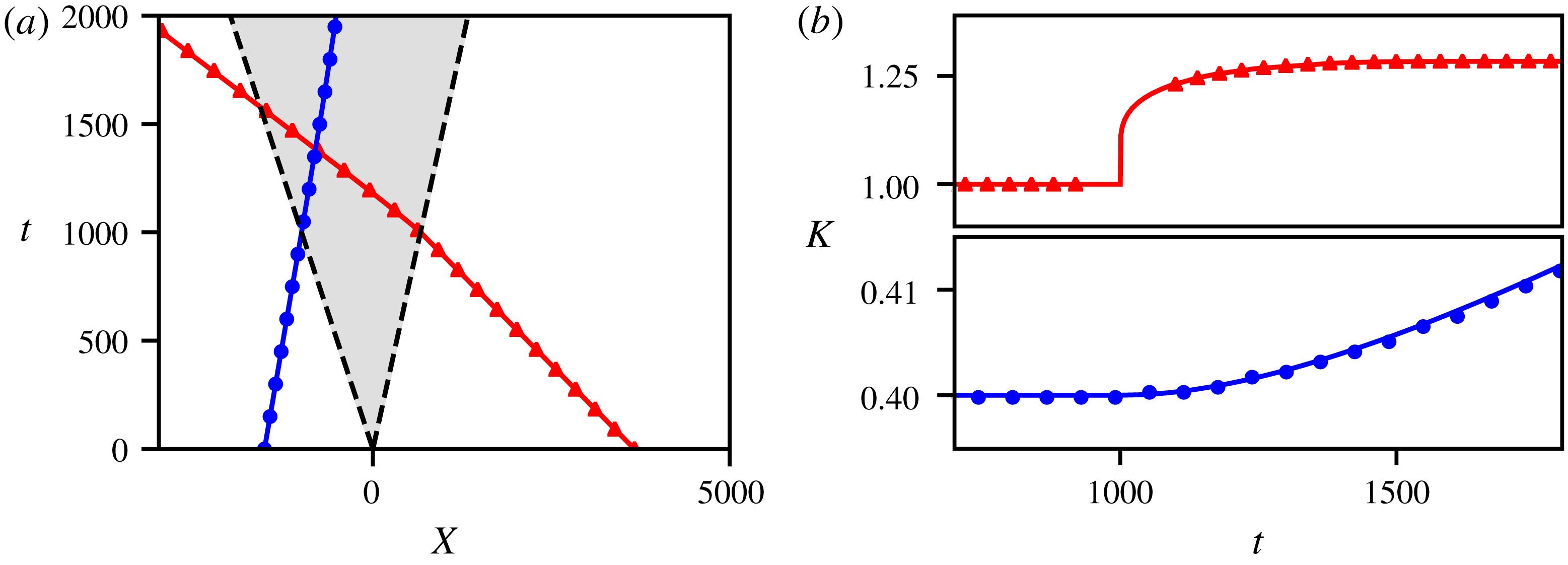
Figure 11. (a) Trajectories of wavepacket–DSW interaction. Solid lines correspond to semi-analytical solutions obtained by solving (4.6), (4.10) and markers to the numerical resolution of the corresponding Riemann problem. The triangles (▴▴) correspond to the transmission configuration (left-propagating wavepacket with $k_{+}=1$ ) and the dots ( $\bullet \bullet$ ) correspond to the trapping configuration (right-propagating wavepackets with $k_{-}=0.4$ ). The DSW edge trajectories $x=s_{-}t$ and $x=s_{+}t$ are displayed as dotted lines (- - -), in both cases, we set $\overline{u}_{-}=1$ and $\overline{u}_{+}=0$ . (b) Corresponding temporal variation of the wavenumbers along the wavepacket trajectories. Solid lines correspond to the semi-analytical solution $K(t)=k(\overline{u}(X(t),t))$ where $k(\overline{u})$ has been determined by solving (4.10) numerically.

We now verify that the obtained integral curves for wavepacket–DSW interaction are consistent with the transmission relation (3.7) for PW–RW interaction, as required by hydrodynamic reciprocity. In the transmission configuration, where $k(\overline{u}_{-})>k_{c}=\sqrt{(2/3)(\overline{u}_{-}-\overline{u}_{+})}$ (see (3.9)), the wave curve $k(\overline{u})$ is represented by a solid curve in figure 10(a) that connects $\overline{u}=\overline{u}_{+}$ to $\overline{u}=\overline{u}_{-}$ and, for a given incident wavenumber $k_{+}$ , the transmitted wavenumber is obtained by evaluating $k(\overline{u}_{-})$ . Figure 10(b) shows the comparison of the transmitted wavenumber $k(\overline{u}_{-})$ evaluated by the above semi-analytical procedure with the value $k_{-}=\sqrt{k_{+}^{2}+(2/3)(\overline{u}_{-}-\overline{u}_{+})}$ obtained from the wavepacket–RW transmission condition (3.7) by invoking hydrodynamic reciprocity. The agreement confirms the validity of the mean field approximation and its consistency with hydrodynamic reciprocity.

As expected, the behaviour of wave curves $k(\overline{u})$ is drastically different for the trapping configuration, when $k(\overline{u}_{-})<k_{c}$ . In this case, the curves $k(\overline{u})$ (represented by dashed curves in figure 10 a) do not connect $\overline{u}=\overline{u}_{-}$ to $\overline{u}=\overline{u}_{+}$ anymore, implying that the wavepacket initially placed at $x=X_{0}<0$ cannot reach the mean flow $\overline{u}=\overline{u}_{+}$ (trapping). Interestingly, these trapping wave curves $k(\overline{u})$ are multi-valued, which implies that wavepackets with initial parameters $\overline{u}=\overline{u}_{-},k<k_{c}$ will return, asymptotically as $t\rightarrow \infty$ , to the DSW harmonic edge where $\overline{u}=\overline{u}_{-}$ . More specifically, the point $\overline{u}=\overline{u}_{-},k=k_{c}$ plays the role of an attractor in the parameter space for trapping configurations, such that all the trapped wavepackets’ wavenumbers converge to the same value $k_{c}$ with time. This filtering behaviour is unusual and drastically different from wavepacket–RW trapping (see § 4.3), where the wavepacket trajectory is single valued and $k\rightarrow 0$ as $t\rightarrow \infty$ .

We now compare the wavepacket dynamics obtained through our modulation analysis with the numerical solution of the KdV equation with initial conditions given by the partial Riemann data (4.1) (see appendix A for details of the numerical procedure employed to trace the dynamics of a wavepacket inside a DSW). Figure 11 displays trajectories for the transmitted and trapped wavepacket configurations, and snapshots of the envelope $a(x,t)$ and the Fourier transform of $\unicode[STIX]{x1D711}(x,t)$ for the corresponding numerical simulation are presented in figure 12. The agreement of the numerical simulations with the analytical predictions in figure 11 represents a further confirmation of the mean field approximation employed in the derivation of the basic ODE (4.10).

Similar to the interaction with a RW, the group velocity of the linear wavepacket is not constant inside the DSW – but now the wavepacket accelerates in the transmission case and simultaneously experiences a wavenumber increase. Here, however, the determination of the wavenumber $K(t)$ is not everywhere possible in the numerical simulation, see figure 11(b). This becomes obvious when one follows the evolution of the amplitude of the Fourier transform $|\tilde{\unicode[STIX]{x1D711}}(k,t)|$ of the linear field $\unicode[STIX]{x1D711}(x,t)$ along with the envelope $a(x,t)$ of the field itself (cf. figure 12). Initially in our simulations, both distributions have a Gaussian shape, but the Fourier transform of the amplitude distribution loses its unimodality when the wavepacket initially interacts with the leading, soliton, edge of the DSW (see figure 12 a at $t=1000$ ). In fact, close to the soliton edge the mean flow gradient $\overline{u}_{x}$ is logarithmically singular (Gurevich & Pitaevskii Reference Gurevich and Pitaevskii1974; El Reference El2005), see figure 2, and the wavenumber field $k(x,t)$ varies significantly over the extent of the wavepacket. As a result, we are no longer in a position to define a nearly monochromatic carrier wave in the wavepacket. Figure 12 shows that the quasi-monochromatic wavepacket structure is recovered when the interaction with the DSW edge is over. Its wavenumber is still described by the adiabatic analytical result while the wavepacket propagates in the region where $\overline{u}$ is almost constant over the wavepacket extension. Ultimately $K=k_{-}$ , where $k_{-}$ is given by the relation (3.7), when the wavepacket is no longer interacting with the DSW due to hydrodynamic reciprocity.

The above described logarithmic divergence of the mean field gradient is absent in wavepacket–RW interactions considered in the previous section, where $\overline{u}=x/t$ inside the hydrodynamic state such that $k_{x}\propto \overline{u}_{x}$ remains finite but exhibits a discontinuity. We still observe a similar, slight deviation from monochromaticity in wavepacket–RW interaction at the initial stage, cf. figure 8  $t=500$ , with $\overline{u}$ varying significantly along the extension of the wavepacket. This behaviour, expectedly, does not appear in the wavepacket–DSW trapping interaction (see figure 12 b), where the wavepacket, coming from the left of the hydrodynamic state, only interacts with the slowly varying part of the mean flow.

Figure 12. Numerical evolution of wavepacket–DSW interaction, in the transmitted configuration (a) and in the trapped configuration (b). The first column displays the wavepacket’s envelope amplitude $a(x,t)$ and the positions of the RW edges are indicated by dotted lines (- - -). The second column displays the amplitude of the wavepacket’s Fourier transform.

Similar to wavepacket–RW interaction, we consider the phase shift of the wavepacket transmitted through the DSW. The numerical results are presented in figure 9(b) and are in agreement with the value predicted analytically in (4.9) via hydrodynamic reciprocity.

We note in conclusion that the trapping configuration is somewhat more difficult to treat analytically using the mean field approach employed in other cases. Although the trajectory, as well as the dominant wavenumber of the wavepacket, can be approximately described by our theory for short time evolution (see figure 11), we numerically observe that the dynamics of the DSW is no longer decoupled from the dynamics of the linear wave, and the distinction between the two structures becomes less and less pronounced after a sufficiently long time.