Hostname: page-component-8448b6f56d-gtxcr Total loading time: 0 Render date: 2024-04-24T06:47:58.269Z Has data issue: false hasContentIssue false
  • English
  • Français

Interfaces of uniform momentum zones in turbulent boundary layers

Published online by Cambridge University Press:  12 May 2017

Charitha M. de Silva Open the ORCID record for Charitha M. de Silva [Opens in a new window] ,
Jimmy Philip ,
Nicholas Hutchins  and
Ivan Marusic
Charitha M. de Silva*
Affiliation:
Department of Mechanical Engineering, The University of Melbourne, Victoria 3010, Australia
Jimmy Philip
Affiliation:
Department of Mechanical Engineering, The University of Melbourne, Victoria 3010, Australia
Nicholas Hutchins
Affiliation:
Department of Mechanical Engineering, The University of Melbourne, Victoria 3010, Australia
Ivan Marusic
Affiliation:
Department of Mechanical Engineering, The University of Melbourne, Victoria 3010, Australia
*
†Email address for correspondence: desilvac@unimelb.edu.au
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we examine the characteristics of the interfaces that demarcate regions of relatively uniform streamwise momentum in turbulent boundary layers. The analysis utilises particle image velocimetry databases that span more than an order of magnitude of friction Reynolds number (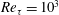$Re_{\unicode[STIX]{x1D70F}}=10^{3}$–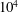$10^{4}$), enabling us to provide a detailed description of the interfacial layers as a function of Reynolds number. As reported by Adrian et al. (J. Fluid Mech., vol. 422, 2000, pp. 1–54), these interfaces appear as persistent regions of strong shear with distinct patches of vorticity consistent with a packet-like structure. Here, however, we treat these interfaces as continuous lines, thus averaging the properties of the vortical patches, and find that their geometry is highly contorted and exhibits self-similarity across a wide range of scales. Specifically, the lengths of the edges of uniform momentum zones exhibit a power-law behaviour with a fractal scaling that has a constant exponent across the boundary layer, while the topmost edge or the turbulent/non-turbulent interface shows a sudden increase in the exponent. The accompanying sharp changes in velocity that occur at these edges are found to change in magnitude as a function of wall-normal height, being larger closer to the wall. Further, a Reynolds number invariance is exhibited when the magnitude of the step-like changes in velocity is scaled by the skin-friction velocity, meanwhile, the width across which it occurs is shown to be of the order of the Taylor microscale. Based on these quantitative measures, the Reynolds number scaling observed and the persistent presence of sharp changes in momentum in turbulent boundary layers, a simple model is used to reconstruct the mean velocity profile. Insight gained from the model enhances our understanding of how instantaneous phenomena (such as a zonal-like structural arrangement) manifests in the averaged flow statistics and confirms that the instantaneous momentum in a turbulent boundary layer appears to mainly consist of a step-like profile as a function of wall-normal distance.

JFM classification

Boundary Layers: Boundary layer structure Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 820 , 10 June 2017 , pp. 451 - 478
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J., Meinhart, C. D. & Tomkins, C. D. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.Google Scholar
del Alamo, J. C., Jiménez, J., Zandonade, P. & Moser, R. D. 2004 Scaling of the energy spectra of turbulent channels. J. Fluid Mech. 500, 135–144.Google Scholar
Anand, R. K., Boersma, B. J. & Agrawal, A. 2009 Detection of turbulent/non-turbulent interface for an axisymmetric turbulent jet: evaluation of known criteria and proposal of a new criterion. Exp. Fluids 47 (6), 995–1007.CrossRefGoogle Scholar
Bisset, D. K., Hunt, J. C. R. & Rogers, M. M. 2002 The turbulent/non-turbulent interface bounding a far wake. J. Fluid Mech. 451, 383–410.Google Scholar
Blackwelder, R. F. & Kovasznay, L. S. G. 1972 Time scales and correlations in a turbulent boundary layer. Phys. Fluids 15, 1545–1554.Google Scholar
Borrell, G. & Jiménez, J. 2016 Properties of the turbulent/non-turbulent interface in boundary layers. J. Fluid Mech. 801, 554–596.CrossRefGoogle Scholar
Brown, G. L. & Roshko, A. 1974 On density effects and large structure in turbulent mixing layers. J. Fluid Mech. 64 (4), 775–816.CrossRefGoogle Scholar
Chauhan, K. A., Monkewitz, P. A. & Nagib, H. M. 2009 Criteria for assessing experiments in zero pressure gradient boundary layers. Fluid Dyn. Res. 41 (2), 021404.CrossRefGoogle Scholar
Chauhan, K., Philip, J. & Marusic, I. 2014a Scaling of the turbulent/non-turbulent interface in boundary layers. J. Fluid Mech. 751, 298–328.Google Scholar
Chauhan, K., Philip, J., de Silva, C. M., Hutchins, N. & Marusic, I. 2014b The turbulent/non-turbulent interface and entrainment in a boundary layer. J. Fluid Mech. 742, 119–151.Google Scholar
Christensen, K. T. & Adrian, R. J. 2001 Statistical evidence of hairpin vortex packets in wall turbulence. J. Fluid Mech. 431, 433–443.CrossRefGoogle Scholar
Corrsin, S. & Kistler, A. L. 1955 Free-stream boundaries of turbulent flows. NACA Tech. Note 1244.Google Scholar
Eisma, J., Westerweel, J., Ooms, G. & Elsinga, G. E. 2015 Interfaces and internal layers in a turbulent boundary layer. Phys. Fluids 27 (5), 055103.CrossRefGoogle Scholar
Hambleton, W. T., Hutchins, N. & Marusic, I. 2006 Simultaneous orthogonal-plane particle image velocimetry measurements in a turbulent boundary layer. J. Fluid Mech. 560, 53–64.Google Scholar
Head, M. R. & Bandyopadhyay, P. 1981 New aspects of turbulent boundary-layer structure. J. Fluid Mech. 107, 297–338.Google Scholar
Herpin, S., Stanislas, M., Foucaut, J. M. & Coudert, S. 2013 Influence of the Reynolds number on the vortical structures in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 716, 5–50.CrossRefGoogle Scholar
Heskestad, G. 1965 Hot-wire measurements in a plane turbulent jet. Trans. ASME J. Appl. Mech. 32 (4), 721–734.CrossRefGoogle Scholar
Holzner, M. & Lüthi, B. 2011 Laminar superlayer at the turbulence boundary. Phys. Rev. Lett. 106 (13), 134503.CrossRefGoogle ScholarPubMed
Ishihara, T., Kaneda, Y. & Hunt, J. C. R. 2013 Thin shear layers in high Reynolds number turbulence – DNS results. Flow Turbul. Combust. 91 (4), 895–929.Google Scholar
Ishihara, T., Ogasawara, H. & Hunt, J. C. R. 2015 Analysis of conditional statistics obtained near the turbulent/non-turbulent interface of turbulent boundary layers. J. Fluids Struct. 53, 50–57.CrossRefGoogle Scholar
Jiménez, J., Hoyas, S., Simens, M. P. & Mizuno, Y. 2010 Turbulent boundary layers and channels at moderate Reynolds numbers. J. Fluid Mech. 657, 335–360.Google Scholar
Krug, D., philip, J. & Marusic, I. 2017 Uniform momentum zones in turbulent boundary layers. J. Fluid Mech. 811, 421–435.Google Scholar
Kwon, Y. S., Philip, J., de Silva, C. M., Monty, N. & Hutchins, J. P. 2014 The quiescent core of turbulent channel flow. J. Fluid Mech. 751, 228–254.Google Scholar
Mandelbrot, B. B. 1982 The Fractal Geometry of Nature. W. H. Freeman.Google Scholar
Mathew, J. & Basu, A. J. 2002 Some characteristics of entrainment at a cylindrical turbulence boundary. Phys. Fluids 14 (7), 2065–2072.Google Scholar
Meinhart, C. D. & Adrian, R. J. 1995 On the existence of uniform momentum zones in a turbulent boundary layer. Phys. Fluids 7, 694.Google Scholar
Meneveau, C. & Sreenivasan, K. R. 1990 Interface dimension in intermittent turbulence. Phys. Rev. A 41 (4), 2246.Google Scholar
Miller, P. L. & Dimotakis, P. E. 1991 Stochastic geometric properties of scalar interfaces in turbulent jets. Phys. Fluids A 3 (1), 168–177.Google Scholar
Mistry, D., Philip, J., Dawson, J. R. & Marusic, I. 2016 Entrainment at multi-scales across the turbulent/nonturbulent interface in an axisymmetric jet. J. Fluid Mech. 802, 690–725.CrossRefGoogle Scholar
Morrill-Winter, C. & Klewicki, J. 2013 Influences of boundary layer scale separation on the vorticity transport contribution to turbulent inertia. Phys. Fluids 25 (1), 015108.Google Scholar
Perry, A. E. & Chong, M. S. 1982 On the mechanism of wall turbulence. J. Fluid Mech. 119 (173), 106–121.Google Scholar
Philip, J. & Marusic, I. 2012 Large-scale eddies and their role in entrainment in turbulent jets and wakes. Phys. Fluids 24 (5), 055108.CrossRefGoogle Scholar
Prasad, R. R. & Sreenivasan, K. R. 1989 Scalar interfaces in digital images of turbulent flows. Exp. Fluids 7 (4), 259–264.Google Scholar
Priyadarshana, P. J. A., Klewicki, J. C., Treat, S. & Foss, J. F. 2007 Statistical structure of turbulent-boundary-layer velocity–vorticity products at high and low Reynolds numbers. J. Fluid Mech. 570, 307–346.Google Scholar
Robinson, S. K. 1991 Coherent motions in the turbulent boundary layer. Annu. Rev. Fluid Mech. 23 (1), 601–639.Google Scholar
Semin, N., Golub, V., Elsinga, G. & Westerweel, J. 2011 Laminar superlayer in a turbulent boundary layer. Tech. Phys. Lett. 37 (12), 1154–1157.Google Scholar
Siebesma, A. P. & Jonker, H. J. J. 2000 Anomalous scaling of cumulus cloud boundaries. Phys. Rev. Lett. 85 (1), 214–217.Google Scholar
Sillero, J. A., Jiménez, J. & Moser, R. D. 2013 One-point statistics for turbulent wall-bounded flows at Reynolds numbers up to 𝛿+ = 2000. Phys. Fluids 25 (10), 105102.Google Scholar
da Silva, C. B., Hunt, J. C. R., Eames, I. & Westerweel, J. 2014 Interfacial layers between regions of different turbulence intensity. Annu. Rev. Fluid Mech. 46, 567–590.Google Scholar
da Silva, C. B. & Taveira, R. R. 2010 The thickness of the turbulent/nonturbulent interface is equal to the radius of the large vorticity structures near the edge of the shear layer. Phys. Fluids 22 (12), 121702.Google Scholar
de Silva, C. M., Chauhan, K. A., Atkinson, C. H., Buchmann, N. A., Hutchins, N., Soria, J. & Marusic, I. 2015 Implementation of large scale PIV measurements for wall bounded turbulence at high Reynolds numbers. In 18th Australasian Fluid Mechanics Conference, Australian Fluid Mechanics Society.Google Scholar
de Silva, C. M., Gnanamanickam, E. P., Atkinson, C., Buchmann, N. A., Hutchins, N., Soria, J. & Marusic, I. 2014 High spatial range velocity measurements in a high Reynolds number turbulent boundary layer. Phys. Fluids 26 (2), 025117.Google Scholar
de Silva, C. M., Hutchins, N. & Marusic, I. 2016 Uniform momentum zones in turbulent boundary layers. J. Fluid Mech. 786, 309–331.Google Scholar
de Silva, C. M., Philip, J., Chauhan, K., Meneveau, C. & Marusic, I. 2013 Multiscale geometry and scaling of the turbulent-nonturbulent interface in high Reynolds number boundary layers. Phys. Rev. Lett. 111, 044501.Google Scholar
de Silva, C. M., Squire, D. T., Hutchins, N. & Marusic, I. 2012 Towards capturing large scale coherent structures in boundary layers using particle image velocimetry. In Proceedings of the 6th Australian Conference on Laser Diagnostics in Fluid Mechanics and Combustion, pp. 1–4. University of Melbourne.Google Scholar
Sreenivasan, K. R. & Meneveau, C. 1986 The fractal facets of turbulence. J. Fluid Mech. 173 (1), 357–386.Google Scholar
Sreenivasan, K. R., Ramshankar, R. & Meneveau, C. 1989 Mixing, entrainment and fractal dimensions of surfaces in turbulent flows. Proc. R. Soc. Lond. A 421 (1860), 79–108.Google Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. MIT.Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow, 2nd edn. Cambridge University Press.Google Scholar
Westerweel, J., Fukushima, C., Pedersen, J. M. & Hunt, J. C. R. 2005 Mechanics of the turbulent-nonturbulent interface of a jet. Phys. Rev. Lett. 95, 174501.Google Scholar
Westerweel, J., Fukushima, C., Pedersen, J. M. & Hunt, J. C. R. 2009 Momentum and scalar transport at the turbulent/non-turbulent interface of a jet. J. Fluid Mech. 631, 199–230.Google Scholar