Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Riols, A.
Rincon, F.
Cossu, C.
Lesur, G.
Longaretti, P.-Y.
Ogilvie, G. I.
and
Herault, J.
2013.
Global bifurcations to subcritical magnetorotational dynamo action in Keplerian shear flow.
Journal of Fluid Mechanics,
Vol. 731,
Issue. ,
p.
1.
Gallet, Basile
and
Young, William R.
2013.
A two-dimensional vortex condensate at high Reynolds number.
Journal of Fluid Mechanics,
Vol. 715,
Issue. ,
p.
359.
Cvitanović, Predrag
2013.
Recurrent flows: the clockwork behind turbulence.
Journal of Fluid Mechanics,
Vol. 726,
Issue. ,
p.
1.
Kim, Sun -Chul
and
Okamoto, Hisashi
2014.
The generalized Proudman–Johnson equation and its singular perturbation problems.
Japan Journal of Industrial and Applied Mathematics,
Vol. 31,
Issue. 3,
p.
541.
Dong, Chengwei
and
Lan, Yueheng
2014.
Organization of spatially periodic solutions of the steady Kuramoto–Sivashinsky equation.
Communications in Nonlinear Science and Numerical Simulation,
Vol. 19,
Issue. 6,
p.
2140.
Gibson, J. F.
and
Brand, E.
2014.
Spanwise-localized solutions of planar shear flows.
Journal of Fluid Mechanics,
Vol. 745,
Issue. ,
p.
25.
Suri, Balachandra
Tithof, Jeffrey
Mitchell, Radford
Grigoriev, Roman O.
and
Schatz, Michael F.
2014.
Velocity profile in a two-layer Kolmogorov-like flow.
Physics of Fluids,
Vol. 26,
Issue. 5,
Waugh, Iain C.
Kashinath, K.
and
Juniper, Matthew P.
2014.
Matrix-free continuation of limit cycles and their bifurcations for a ducted premixed flame.
Journal of Fluid Mechanics,
Vol. 759,
Issue. ,
p.
1.
Lucas, Dan
and
Kerswell, Rich
2014.
Spatiotemporal dynamics in two-dimensional Kolmogorov flow over large domains.
Journal of Fluid Mechanics,
Vol. 750,
Issue. ,
p.
518.
Wedin, H.
Bottaro, A.
Hanifi, A.
and
Zampogna, G.
2014.
Unstable flow structures in the Blasius boundary layer.
The European Physical Journal E,
Vol. 37,
Issue. 4,
Park, Jae Sung
and
Graham, Michael D.
2015.
Exact coherent states and connections to turbulent dynamics in minimal channel flow.
Journal of Fluid Mechanics,
Vol. 782,
Issue. ,
p.
430.
Hiruta, Yoshiki
and
Toh, Sadayoshi
2015.
Solitary solutions including spatially localized chaos and their interactions in two-dimensional Kolmogorov flow.
Physical Review E,
Vol. 92,
Issue. 6,
Lucas, Dan
and
Kerswell, Rich R.
2015.
Recurrent flow analysis in spatiotemporally chaotic 2-dimensional Kolmogorov flow.
Physics of Fluids,
Vol. 27,
Issue. 4,
Wedin, Håkan
Cherubini, Stefania
and
Bottaro, Alessandro
2015.
Effect of plate permeability on nonlinear stability of the asymptotic suction boundary layer.
Physical Review E,
Vol. 92,
Issue. 1,
Rawat, Subhandu
Cossu, Carlo
Hwang, Yongyun
and
Rincon, François
2015.
On the self-sustained nature of large-scale motions in turbulent Couette flow.
Journal of Fluid Mechanics,
Vol. 782,
Issue. ,
p.
515.
Fedele, Francesco
Abessi, Ozeair
and
Roberts, Philip J.
2015.
Symmetry reduction of turbulent pipe flows.
Journal of Fluid Mechanics,
Vol. 779,
Issue. ,
p.
390.
Beaume, Cédric
Knobloch, Edgar
Chini, Gregory P
and
Julien, Keith
2015.
Exact coherent structures in an asymptotically reduced description of parallel shear flows.
Fluid Dynamics Research,
Vol. 47,
Issue. 1,
p.
015504.
Byrne, Greg
Marcotte, Christopher D.
and
Grigoriev, Roman O.
2015.
Exact coherent structures and chaotic dynamics in a model of cardiac tissue.
Chaos: An Interdisciplinary Journal of Nonlinear Science,
Vol. 25,
Issue. 3,
Kim, Sun-Chul
and
Okamoto, Hisashi
2015.
Unimodal patterns appearing in the Kolmogorov flows at large Reynolds numbers.
Nonlinearity,
Vol. 28,
Issue. 9,
p.
3219.
Jiménez, Javier
and
Lozano-Durán, Adrián
2016.
Progress in Wall Turbulence 2.
Vol. 23,
Issue. ,
p.
37.
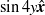 $\sin 4y\hat {\boldsymbol{x}} $ on the torus
$\sin 4y\hat {\boldsymbol{x}} $ on the torus 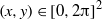 $(x, y)\in \mathop{[0, 2\mathrm{\pi} ] }\nolimits ^{2} $ with the purpose of extracting simple invariant sets or ‘exact recurrent flows’ embedded in this turbulence. Each recurrent flow represents a sustained closed cycle of dynamical processes which underpins the turbulence. These are used to reconstruct the turbulence statistics using periodic orbit theory. The approach is found to be reasonably successful at a low value of the forcing where the flow is close to but not fully in its asymptotic (strongly) turbulent regime. Here, a total of 50 recurrent flows are found with the majority buried in the part of phase space most populated by the turbulence giving rise to a good reproduction of the energy and dissipation p.d.f. However, at higher forcing amplitudes now in the asymptotic turbulent regime, the generated turbulence data set proves insufficiently long to yield enough recurrent flows to make viable predictions. Despite this, the general approach seems promising providing enough simulation data is available since it is open to extensive automation and naturally generates dynamically important exact solutions for the flow.
$(x, y)\in \mathop{[0, 2\mathrm{\pi} ] }\nolimits ^{2} $ with the purpose of extracting simple invariant sets or ‘exact recurrent flows’ embedded in this turbulence. Each recurrent flow represents a sustained closed cycle of dynamical processes which underpins the turbulence. These are used to reconstruct the turbulence statistics using periodic orbit theory. The approach is found to be reasonably successful at a low value of the forcing where the flow is close to but not fully in its asymptotic (strongly) turbulent regime. Here, a total of 50 recurrent flows are found with the majority buried in the part of phase space most populated by the turbulence giving rise to a good reproduction of the energy and dissipation p.d.f. However, at higher forcing amplitudes now in the asymptotic turbulent regime, the generated turbulence data set proves insufficiently long to yield enough recurrent flows to make viable predictions. Despite this, the general approach seems promising providing enough simulation data is available since it is open to extensive automation and naturally generates dynamically important exact solutions for the flow.
