Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Fiscaletti, D.
Westerweel, J.
and
Elsinga, G. E.
2014.
Long-range μPIV to resolve the small scales in a jet at high Reynolds number.
Experiments in Fluids,
Vol. 55,
Issue. 9,
Rabey, P. K.
Wynn, A.
and
Buxton, O. R. H.
2015.
The kinematics of the reduced velocity gradient tensor in a fully developed turbulent free shear flow.
Journal of Fluid Mechanics,
Vol. 767,
Issue. ,
p.
627.
Fiscaletti, D.
Ganapathisubramani, B.
and
Elsinga, G. E.
2015.
Amplitude and frequency modulation of the small scales in a jet.
Journal of Fluid Mechanics,
Vol. 772,
Issue. ,
p.
756.
Lawson, J. M.
and
Dawson, J. R.
2015.
On velocity gradient dynamics and turbulent structure.
Journal of Fluid Mechanics,
Vol. 780,
Issue. ,
p.
60.
Lozano-Durán, Adrián
Holzner, Markus
and
Jiménez, Javier
2015.
Numerically accurate computation of the conditional trajectories of the topological invariants in turbulent flows.
Journal of Computational Physics,
Vol. 295,
Issue. ,
p.
805.
Pumir, Alain
Xu, Haitao
and
Siggia, Eric D.
2016.
Small-scale anisotropy in turbulent boundary layers.
Journal of Fluid Mechanics,
Vol. 804,
Issue. ,
p.
5.
Gan, L.
and
Krogstad, P.-Å.
2016.
Evolution of turbulence and in-plane vortices in the near field flow behind multi-scale planar grids.
Physics of Fluids,
Vol. 28,
Issue. 8,
Graham, J.
Kanov, K.
Yang, X. I. A.
Lee, M.
Malaya, N.
Lalescu, C. C.
Burns, R.
Eyink, G.
Szalay, A.
Moser, R. D.
and
Meneveau, C.
2016.
A Web services accessible database of turbulent channel flow and its use for testing a new integral wall model for LES.
Journal of Turbulence,
Vol. 17,
Issue. 2,
p.
181.
Lozano-Durán, A.
Holzner, M.
and
Jiménez, J.
2016.
Multiscale analysis of the topological invariants in the logarithmic region of turbulent channels at a friction Reynolds number of 932.
Journal of Fluid Mechanics,
Vol. 803,
Issue. ,
p.
356.
Lian, Huan
Soulopoulos, Nikolaos
and
Hardalupas, Yannis
2017.
Evaluation of the topological characteristics of the turbulent flow in a ‘box of turbulence’ through 2D time-resolved particle image velocimetry.
Experiments in Fluids,
Vol. 58,
Issue. 9,
Meneveau, Charles
and
Marusic, Ivan
2017.
Whither Turbulence and Big Data in the 21st Century?.
p.
497.
Zhang, Shuhai
2018.
Tubular limiting stream surface: “tornado” in three-dimensional vortical flow.
Applied Mathematics and Mechanics,
Vol. 39,
Issue. 11,
p.
1631.
Carter, Douglas W.
and
Coletti, Filippo
2018.
Small-scale structure and energy transfer in homogeneous turbulence.
Journal of Fluid Mechanics,
Vol. 854,
Issue. ,
p.
505.
Mansoor, M. M.
Dalton, S. M.
Martinez, A. A.
Desjardins, T.
Charonko, J. J.
and
Prestridge, K. P.
2020.
The effect of initial conditions on mixing transition of the Richtmyer–Meshkov instability.
Journal of Fluid Mechanics,
Vol. 904,
Issue. ,
Li, Zhi-Yu
Xu, Yang
and
Wang, Jin-Jun
2020.
Similarity Parameter for Synthetic Jet Vortex Rings Impinging onto Porous Walls.
AIAA Journal,
Vol. 58,
Issue. 2,
p.
722.
Berk, Tim
and
Coletti, Filippo
2020.
Transport of inertial particles in high-Reynolds-number turbulent boundary layers.
Journal of Fluid Mechanics,
Vol. 903,
Issue. ,
Berk, Tim
and
Coletti, Filippo
2021.
Dynamics of small heavy particles in homogeneous turbulence: a Lagrangian experimental study.
Journal of Fluid Mechanics,
Vol. 917,
Issue. ,
Rojas Carvajal, Tomás E.
Neal, Jacob
and
Amitay, Michael
2024.
Experimental Validation of the Modified Holmén Vortex Identification Method.
AIAA Journal,
Vol. 62,
Issue. 11,
p.
4221.
Sakamoto, Mizuki
and
Shirai, Katsuaki
2024.
Two-dimensional topology analysis on the complex flow driven by corotating disks mounted in a non-axisymmetric enclosure.
Microsystem Technologies,
Vol. 30,
Issue. 2,
p.
155.
Sagharichi, Amir
and
Tachie, Mark Francis
2025.
Analysis of non-equilibrium turbulence dissipation downstream of regular and fractal grids in an open channel flow.
International Journal of Heat and Fluid Flow,
Vol. 114,
Issue. ,
p.
109822.
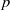 $p$ and
$p$ and 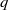 $q$ of the reduced
$q$ of the reduced 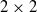 $2\times 2$ velocity gradient tensor (VGT) formed from a two-dimensional (2D) slice of an incompressible three-dimensional (3D) flow. Using data from both 2D particle image velocimetry (PIV) measurements and 3D direct numerical simulations of various turbulent flows, we show that the joint probability density functions (p.d.f.s) of
$2\times 2$ velocity gradient tensor (VGT) formed from a two-dimensional (2D) slice of an incompressible three-dimensional (3D) flow. Using data from both 2D particle image velocimetry (PIV) measurements and 3D direct numerical simulations of various turbulent flows, we show that the joint probability density functions (p.d.f.s) of 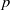 $p$ and
$p$ and 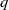 $q$ exhibit a common characteristic asymmetric shape consistent with
$q$ exhibit a common characteristic asymmetric shape consistent with 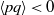 $\langle pq\rangle \lt 0$ . An explanation for this inequality is proposed. Assuming local homogeneity we derive
$\langle pq\rangle \lt 0$ . An explanation for this inequality is proposed. Assuming local homogeneity we derive 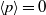 $\langle p\rangle = 0$ and
$\langle p\rangle = 0$ and 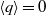 $\langle q\rangle = 0$ . With the addition of local isotropy the sign of
$\langle q\rangle = 0$ . With the addition of local isotropy the sign of 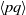 $\langle pq\rangle $ is proved to be the same as that of the skewness of
$\langle pq\rangle $ is proved to be the same as that of the skewness of 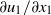 $\partial {u}_{1} / \partial {x}_{1} $ , hence negative. This suggests that the observed asymmetry in the joint p.d.f.s of
$\partial {u}_{1} / \partial {x}_{1} $ , hence negative. This suggests that the observed asymmetry in the joint p.d.f.s of 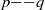 $p{{\ndash}}q$ stems from the universal predominance of vortex stretching at the smallest scales. Some advantages of this joint p.d.f. compared with that of
$p{{\ndash}}q$ stems from the universal predominance of vortex stretching at the smallest scales. Some advantages of this joint p.d.f. compared with that of 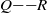 $Q{{\ndash}}R$ obtained from the full
$Q{{\ndash}}R$ obtained from the full 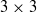 $3\times 3$ VGT are discussed. Analysing the eigenvalues of the reduced strain-rate matrix associated with the reduced VGT, we prove that in some cases the 2D data can unambiguously discriminate between the bi-axial (sheet-forming) and axial (tube-forming) strain-rate configurations of the full
$3\times 3$ VGT are discussed. Analysing the eigenvalues of the reduced strain-rate matrix associated with the reduced VGT, we prove that in some cases the 2D data can unambiguously discriminate between the bi-axial (sheet-forming) and axial (tube-forming) strain-rate configurations of the full 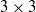 $3\times 3$ strain-rate tensor.
$3\times 3$ strain-rate tensor.
