Article contents
The kinematic genesis of vortex formation due to finite rotation of a plate in still fluid
Published online by Cambridge University Press: 02 February 2018
Abstract
We present a combined experimental and numerical study of an idealized model of the propulsive stroke of the turning manoeuvre in fish. Specifically, we use the framework of Lagrangian coherent structures (LCSs) to describe the kinematics of the flow that results from a thin plate performing a large angle rotation about its tip in still fluid. Temporally and spatially well-resolved velocity fields are obtained using a two-dimensional, incompressible finite-volume solver, and are validated by comparisons with experimentally measured velocity fields and alternate numerical simulations. We then implement the recently proposed variational theory of LCSs to extract the hyperbolic and elliptic LCSs in the numerically generated velocity fields. Detailed LCS analysis is performed for a plate motion profile described by 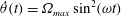 $\dot{\unicode[STIX]{x1D703}}(t)=\unicode[STIX]{x1D6FA}_{max}\sin ^{2}(\unicode[STIX]{x1D714}t)$ during
$\dot{\unicode[STIX]{x1D703}}(t)=\unicode[STIX]{x1D6FA}_{max}\sin ^{2}(\unicode[STIX]{x1D714}t)$ during 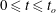 $0\leqslant t\leqslant t_{o}$ and zero otherwise. The stopping time
$0\leqslant t\leqslant t_{o}$ and zero otherwise. The stopping time 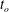 $t_{o}$ is given by
$t_{o}$ is given by 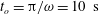 $t_{o}=\unicode[STIX]{x03C0}/\unicode[STIX]{x1D714}=10~\text{s}$ , the value of
$t_{o}=\unicode[STIX]{x03C0}/\unicode[STIX]{x1D714}=10~\text{s}$ , the value of 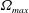 $\unicode[STIX]{x1D6FA}_{max}$ chosen to give a stopping angle of
$\unicode[STIX]{x1D6FA}_{max}$ chosen to give a stopping angle of 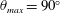 $\unicode[STIX]{x1D703}_{max}=90^{\circ }$ , resulting in a Reynolds number
$\unicode[STIX]{x1D703}_{max}=90^{\circ }$ , resulting in a Reynolds number 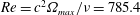 $Re=c^{2}\unicode[STIX]{x1D6FA}_{max}/\unicode[STIX]{x1D708}=785.4$ , where
$Re=c^{2}\unicode[STIX]{x1D6FA}_{max}/\unicode[STIX]{x1D708}=785.4$ , where  $c$ is the plate chord length and
$c$ is the plate chord length and 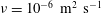 $\unicode[STIX]{x1D708}=10^{-6}~\text{m}^{2}~\text{s}^{-1}$ the kinematic viscosity of water. The flow comprises a starting and a stopping vortex, resulting in a pair of oppositely signed vortices of unequal strengths that move away from the plate in a direction closely aligned with the final plate orientation at
$\unicode[STIX]{x1D708}=10^{-6}~\text{m}^{2}~\text{s}^{-1}$ the kinematic viscosity of water. The flow comprises a starting and a stopping vortex, resulting in a pair of oppositely signed vortices of unequal strengths that move away from the plate in a direction closely aligned with the final plate orientation at 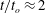 $t/t_{o}\approx 2$ . The hyperbolic LCSs are shown to encompass the fluid material that is advected away from the plate for
$t/t_{o}\approx 2$ . The hyperbolic LCSs are shown to encompass the fluid material that is advected away from the plate for 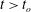 $t>t_{o}$ , henceforth referred to as the advected bulk. The starting and stopping vortices, identified using elliptic LCSs and hence more objective than Eulerian vortex detection methods, constitute only around two thirds of the advected bulk area. The advected bulk is traced back to
$t>t_{o}$ , henceforth referred to as the advected bulk. The starting and stopping vortices, identified using elliptic LCSs and hence more objective than Eulerian vortex detection methods, constitute only around two thirds of the advected bulk area. The advected bulk is traced back to 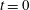 $t=0$ to identify five distinct lobes of fluid that eventually form the advected bulk, and hence map the long-term fate of various regions in the fluid at
$t=0$ to identify five distinct lobes of fluid that eventually form the advected bulk, and hence map the long-term fate of various regions in the fluid at 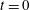 $t=0$ . The five different lobes of fluid are then shown to be delineated by repelling LCS boundaries at
$t=0$ . The five different lobes of fluid are then shown to be delineated by repelling LCS boundaries at 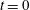 $t=0$ . The linear momentum of the advected bulk region is shown to account for approximately half of the total impulse experienced by the plate in the direction of its final orientation, thus establishing its dynamical significance. We provide direct experimental evidence for the kinematic relevance of hyperbolic and elliptic LCSs using novel dye visualization experiments, and also show that attracting hyperbolic LCSs provide objective characterization of the spiral structures often observed in vortical flows. We conclude by showing that qualitatively similar LCSs persist for several other plate motion profiles and stopping angles as well.
$t=0$ . The linear momentum of the advected bulk region is shown to account for approximately half of the total impulse experienced by the plate in the direction of its final orientation, thus establishing its dynamical significance. We provide direct experimental evidence for the kinematic relevance of hyperbolic and elliptic LCSs using novel dye visualization experiments, and also show that attracting hyperbolic LCSs provide objective characterization of the spiral structures often observed in vortical flows. We conclude by showing that qualitatively similar LCSs persist for several other plate motion profiles and stopping angles as well.
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 15
- Cited by


