Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Thebault, Martin
Giroux-Julien, Stéphanie
Timchenko, Victoria
Ménézo, Christophe
and
Reizes, John
2019.
Detailed flow development and indicators of transition in a natural convection flow in a vertical channel.
International Journal of Heat and Mass Transfer,
Vol. 143,
Issue. ,
p.
118502.
Liu, Yang
Bian, Yongning
Zhao, Yongling
Zhang, Shuaikun
and
Suo, Qinghui
2019.
Scaling laws for the transient convective flow in a differentially and linearly heated rectangular cavity at Pr > 1.
Physics of Fluids,
Vol. 31,
Issue. 4,
Zhao, Yongling
Zhao, Pengpeng
Liu, Yang
Xu, Yin
and
Torres, Juan F.
2019.
On the selection of perturbations for thermal boundary layer control.
Physics of Fluids,
Vol. 31,
Issue. 10,
Zhao, Yongling
Lei, Chengwang
and
Patterson, John C.
2019.
PIV measurements of the K-type transition in natural convection boundary layers.
Experimental Thermal and Fluid Science,
Vol. 101,
Issue. ,
p.
62.
Liu, Yang
Zhang, Shuaikun
Huang, Han
Suo, Qinghui
Bian, Yongning
and
Zhao, Yongling
2019.
Enhancing the flow and heat transfer in a convective cavity using symmetrical and adiabatic twin fins.
International Journal of Heat and Mass Transfer,
Vol. 142,
Issue. ,
p.
118447.
Ke, Junhao
Williamson, N.
Armfield, S. W.
McBain, G. D.
and
Norris, S. E.
2019.
Stability of a temporally evolving natural convection boundary layer on an isothermal wall.
Journal of Fluid Mechanics,
Vol. 877,
Issue. ,
p.
1163.
Ke, Junhao
Williamson, N.
Armfield, S. W.
Norris, S. E.
and
Komiya, A.
2020.
Law of the wall for a temporally evolving vertical natural convection boundary layer.
Journal of Fluid Mechanics,
Vol. 902,
Issue. ,
Majdalani, Joseph
and
Xuan, Li-Jun
2020.
On the Kármán momentum-integral approach and the Pohlhausen paradox.
Physics of Fluids,
Vol. 32,
Issue. 12,
Liu, Yang
and
Ren, Sitao
2021.
Receptivity of incompressible convective boundary layers induced by linear thermal forcing.
Physics of Fluids,
Vol. 33,
Issue. 3,
Fan, Yifan
Zhao, Yongling
Torres, Juan F.
Xu, Feng
Lei, Chengwang
Li, Yuguo
and
Carmeliet, Jan
2021.
Natural convection over vertical and horizontal heated flat surfaces: A review of recent progress focusing on underpinnings and implications for heat transfer and environmental applications.
Physics of Fluids,
Vol. 33,
Issue. 10,
Kogawa, Takuma
Okajima, Junnosuke
Komiya, Atsuki
and
Maruyama, Shigenao
2021.
Effect of gas radiation-depended natural convection on the transition of spatially developing boundary layers.
International Journal of Heat and Mass Transfer,
Vol. 177,
Issue. ,
p.
121580.
Thebault, M.
Giroux-Julien, S.
Timchenko, V.
Reizes, J.
and
Ménézo, C.
2021.
Numerical study of the coherent structures in a transitional vertical channel natural convection flow.
Physics of Fluids,
Vol. 33,
Issue. 3,
Zhao, Yongling
Lei, Chengwang
and
Patterson, John C.
2021.
Magnified heat transfer from curved surfaces: A scaling prediction.
Physics of Fluids,
Vol. 33,
Issue. 2,
Zeraati Dizjeh, S.
and
Brinkerhoff, J.
2021.
Stability of buoyancy-driven flow in a vertical channel with one heated wall.
Physics of Fluids,
Vol. 33,
Issue. 8,
Mondal, Razon
Torres, Juan F.
Hughes, Graham
and
Pye, John
2022.
Air curtains for reduction of natural convection heat loss from a heated plate: A numerical investigation.
International Journal of Heat and Mass Transfer,
Vol. 189,
Issue. ,
p.
122709.
Dotto, A.
Barsi, D.
Lengani, D.
Simoni, D.
and
Satta, F.
2022.
Effect of free-stream turbulence properties on different transition routes for a zero-pressure gradient boundary layer.
Physics of Fluids,
Vol. 34,
Issue. 5,
Chen, Yu
and
Gibbons, Nick
2022.
Simulations of Hypersonic Boundary-Layer Transition over a Flat Plate with the Spalart-Allmaras One-Equation BCM Transitional Model.
Mathematics,
Vol. 10,
Issue. 19,
p.
3431.
Maryada, K.R.
Armfield, S.W.
Dhopade, P.
and
Norris, S.E.
2022.
Oblique-mode breakdown of the vertical buoyancy layer.
Journal of Fluid Mechanics,
Vol. 953,
Issue. ,
Mazharmanesh, Soudeh
Tian, Fang-Bao
and
Lei, Chengwang
2023.
Enhancing heat transfer using flow-induced oscillations of a flexible baffle attached to a vertical heated flat surface.
International Journal of Thermal Sciences,
Vol. 194,
Issue. ,
p.
108604.
Maryada, K.R.
Armfield, S.W.
Dhopade, P.
and
Norris, S.E.
2023.
Large-scale motions in a turbulent natural convection boundary layer immersed in a stably stratified environment.
Journal of Fluid Mechanics,
Vol. 967,
Issue. ,
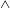 $\wedge$-shaped vortices characterizing the K-type transition are observed for the first time in pure natural convection boundary layers. For exciting the H-type transition, superimposed TS and oblique waves of different frequencies, with the frequency of the oblique waves being half of the frequency of the TS waves, are introduced into the boundary layer. Unlike the three-layer longitudinal vortex structure observed in the K-type transition, a double-layer longitudinal vortex structure is observed in the boundary layer undergoing the H-type transition. The successively staggered
$\wedge$-shaped vortices characterizing the K-type transition are observed for the first time in pure natural convection boundary layers. For exciting the H-type transition, superimposed TS and oblique waves of different frequencies, with the frequency of the oblique waves being half of the frequency of the TS waves, are introduced into the boundary layer. Unlike the three-layer longitudinal vortex structure observed in the K-type transition, a double-layer longitudinal vortex structure is observed in the boundary layer undergoing the H-type transition. The successively staggered 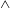 $\wedge$-shaped vortices characterizing the H-type transition are also observed in the downstream boundary layer. The staggered pattern of
$\wedge$-shaped vortices characterizing the H-type transition are also observed in the downstream boundary layer. The staggered pattern of 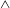 $\wedge$-shaped vortices is considered to be caused by temporal modulation of the TS and oblique waves. Interestingly the flow structures of both the K-type and H-type transitions observed in the natural convection boundary layer are qualitatively similar to those observed in Blasius boundary layers. However, an analysis of turbulence energy production suggests that the turbulence energy production by buoyancy rather than Reynolds stresses dominates the K-type and H-type transitions. In contrast, the turbulence energy production by Reynolds stresses is the only factor contributing to the transition in Blasius boundary layers.
$\wedge$-shaped vortices is considered to be caused by temporal modulation of the TS and oblique waves. Interestingly the flow structures of both the K-type and H-type transitions observed in the natural convection boundary layer are qualitatively similar to those observed in Blasius boundary layers. However, an analysis of turbulence energy production suggests that the turbulence energy production by buoyancy rather than Reynolds stresses dominates the K-type and H-type transitions. In contrast, the turbulence energy production by Reynolds stresses is the only factor contributing to the transition in Blasius boundary layers.