Article contents
Large eddy simulation of the velocity-intermittency structure for flow over a field of symmetric dunes
Published online by Cambridge University Press: 23 September 2016
Abstract
Owing to their frequent occurrence in the natural environment, there has been significant interest in refining our understanding of flow over dunes and other bedforms. Recent work in this area has focused, in particular, on their shear-layer characteristics and the manner by which flow structures are generated. However, field-based studies, are reliant on single-, or multi-point measurements, rather than delimiting flow structures from the velocity gradient tensor, as is possible in numerical work. Here, we extract pointwise time series from a well-resolved large eddy simulation as a means to connect these two approaches. The at-a-point analysis technique is termed the velocity-intermittency quadrant method and relates the fluctuating, longitudinal velocity, 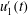 $u_{1}^{\prime }(t)$ , to its fluctuating pointwise Hölder regularity,
$u_{1}^{\prime }(t)$ , to its fluctuating pointwise Hölder regularity, 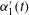 $\unicode[STIX]{x1D6FC}_{1}^{\prime }(t)$ . Despite the difference in boundary conditions, our results agree very well with previous experiments that show the importance, in the region above the dunes, of a quadrant 3 (
$\unicode[STIX]{x1D6FC}_{1}^{\prime }(t)$ . Despite the difference in boundary conditions, our results agree very well with previous experiments that show the importance, in the region above the dunes, of a quadrant 3 ( 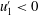 $u_{1}^{\prime }<0$ ,
$u_{1}^{\prime }<0$ , 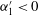 $\unicode[STIX]{x1D6FC}_{1}^{\prime }<0$ ) flow configuration. Our higher density of sampling beneath the shear layer and close to the bedforms relative to experimental work reveals a negative correlation between
$\unicode[STIX]{x1D6FC}_{1}^{\prime }<0$ ) flow configuration. Our higher density of sampling beneath the shear layer and close to the bedforms relative to experimental work reveals a negative correlation between 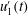 $u_{1}^{\prime }(t)$ and
$u_{1}^{\prime }(t)$ and 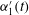 $\unicode[STIX]{x1D6FC}_{1}^{\prime }(t)$ in this region. This consists of two distinct layers, with quadrant 4 (
$\unicode[STIX]{x1D6FC}_{1}^{\prime }(t)$ in this region. This consists of two distinct layers, with quadrant 4 ( 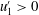 $u_{1}^{\prime }>0$ ,
$u_{1}^{\prime }>0$ ,  $\unicode[STIX]{x1D6FC}_{1}^{\prime }<0$ ) dominant near the wall and quadrant 2 (
$\unicode[STIX]{x1D6FC}_{1}^{\prime }<0$ ) dominant near the wall and quadrant 2 (  $u_{1}^{\prime }<0$ ,
$u_{1}^{\prime }<0$ , 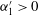 $\unicode[STIX]{x1D6FC}_{1}^{\prime }>0$ ) dominant close to the lower part of the separated shear layer. These results are consistent with a near-wall advection of vorticity into a region downstream of a temporarily foreshortened reattachment region, and the entrainment of slow moving and quiescent fluid into a faster, more turbulent shear layer. A comparison of instantaneous vorticity fields to the velocity-intermittency analysis shows how the pointwise results reflect larger-scale organisation of the flow. We illustrate this using results from two instantaneous datasets. In the former, extreme velocity-intermittency events corresponding to a foreshortened recirculation region (and high pressures on the stoss slope of the dune immediately downstream) arise, and the development of intense flow structures occurs as a consequence. In the other case, development of a ‘skimming flow’ with relatively little exchange between the inner and outer regions results in exceedances because of the coherence associated with this high velocity, high turbulence outer region. Thus, our results shed further light on the characteristics of dune flow in the near-wall region and, importantly for field-based research, show that useful information on flow structure can be obtained from single-point single velocity component measurements.
$\unicode[STIX]{x1D6FC}_{1}^{\prime }>0$ ) dominant close to the lower part of the separated shear layer. These results are consistent with a near-wall advection of vorticity into a region downstream of a temporarily foreshortened reattachment region, and the entrainment of slow moving and quiescent fluid into a faster, more turbulent shear layer. A comparison of instantaneous vorticity fields to the velocity-intermittency analysis shows how the pointwise results reflect larger-scale organisation of the flow. We illustrate this using results from two instantaneous datasets. In the former, extreme velocity-intermittency events corresponding to a foreshortened recirculation region (and high pressures on the stoss slope of the dune immediately downstream) arise, and the development of intense flow structures occurs as a consequence. In the other case, development of a ‘skimming flow’ with relatively little exchange between the inner and outer regions results in exceedances because of the coherence associated with this high velocity, high turbulence outer region. Thus, our results shed further light on the characteristics of dune flow in the near-wall region and, importantly for field-based research, show that useful information on flow structure can be obtained from single-point single velocity component measurements.
Information
- Type
- Papers
- Information
- Copyright
- © 2016 Cambridge University Press
References
- 15
- Cited by


