Hostname: page-component-8448b6f56d-wq2xx Total loading time: 0 Render date: 2024-04-24T01:57:33.829Z Has data issue: false hasContentIssue false
  • English
  • Français

Lift on a steady 2-D symmetric airfoil in viscous uniform shear flow

Published online by Cambridge University Press:  28 December 2017

Patrick R. Hammer Open the ORCID record for Patrick R. Hammer [Opens in a new window] ,
Miguel R. Visbal ,
Ahmed M. Naguib  and
Manoochehr M. Koochesfahani
Patrick R. Hammer*
Affiliation:
Department of Mechanical Engineering, Michigan State University, East Lansing, MI 48824, USA
Miguel R. Visbal
Affiliation:
Aerospace Systems Directorate, Air Force Research Laboratory, Wright-Patterson Air Force Base, OH 45433, USA
Ahmed M. Naguib
Affiliation:
Department of Mechanical Engineering, Michigan State University, East Lansing, MI 48824, USA
Manoochehr M. Koochesfahani
Affiliation:
Department of Mechanical Engineering, Michigan State University, East Lansing, MI 48824, USA
*
†Email address for correspondence: hammerpa@egr.msu.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We present an investigation into the influence of upstream shear on the viscous flow around a steady two-dimensional (2-D) symmetric airfoil at zero angle of attack, and the corresponding loads. In this computational study, we consider the NACA 0012 airfoil at a chord Reynolds number 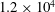$1.2\times 10^{4}$ in an approach flow with uniform positive shear with non-dimensional shear rate varying in the range 0.0–1.0. Results show that the lift force is negative, in the opposite direction to the prediction from Tsien’s inviscid theory for lift generation in the presence of positive shear. A hypothesis is presented to explain the observed sign of the lift force on the basis of the asymmetry in boundary layer development on the upper and lower surfaces of the airfoil, which creates an effective airfoil shape with negative camber. The resulting scaling of the viscous effect with shear rate and Reynolds number is provided. The location of the leading edge stagnation point moves increasingly farther back along the airfoil’s upper surface with increased shear rate, a behaviour consistent with a negatively cambered airfoil. Furthermore, the symmetry in the location of the boundary layer separation point on the airfoil’s upper and lower surfaces in uniform flow is broken under the imposed shear, and the wake vortical structures exhibit more asymmetry with increasing shear rate.

JFM classification

Aerodynamics: Aerodynamics
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 837 , 25 February 2018 , R2
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alpert, P. 1981 Implicit filtering in conjunction with explicit filtering. J. Comput. Phys. 44, 212–219.Google Scholar
Beam, R. & Warming, R. 1978 An implicit factored scheme for the compressible Navier–Stokes equations. AIAA J. 16 (4), 393–402.Google Scholar
Currie, I. G. 1993 Fundamental Mechanics of Fluids. CRC Press, Taylor & Francis Group.Google Scholar
Gaitonde, D. V. & Visbal, M. R.1998 High-order schemes for Navier–Stokes equations: algorithm and implementation into FDL3DI. Tech. Rep. Air Force Research Laboratory.Google Scholar
Gaitonde, D. V. & Visbal, M. R.1999 Further development of a Navier–Stokes solution procedure based on higher-order formulas. AIAA Paper 99-16436.Google Scholar
Hammer, P. R.2016 Computational study on the effect of Reynolds number and motion trajectory asymmetry on the aerodynamics of a pitching airfoil at low Reynolds number. PhD thesis, Michigan State University.Google Scholar
Katz, J. & Plotkin, A. 2001 Low-Speed Aerodynamics, 2nd edn. Cambridge University Press.Google Scholar
Koochesfahani, M. M. 1989 Vortical patterns in the wake of an oscillating airfoil. AIAA J. 27 (9), 1200–1205.Google Scholar
Laitone, E. 1997 Wind tunnel tests of wings at Reynolds numbers below 70 000. Exp. Fluids 23, 405–409.Google Scholar
Lele, S. 1992 Compact finite difference scheme with spectral-like resolution. J. Comput. Phys. 103, 16–42.Google Scholar
Liu, H. & Kawachi, K. 1999 A numerical study of undulatory swimming. J. Comput. Phys. 155, 223–247.Google Scholar
Olson, D. A., Naguib, A. M. & Koochesfahani, M. M. 2016 Experiments on a steady low Reynolds number airfoil in a shear flow. Bull. Am. Phys. Soc. 61, 174.Google Scholar
Payne, F. & Nelson, R. 1985 Aerodynamic characteristics of an airfoil in a nonuniform wind profile. J. Aircraft 22 (1), 5–10.Google Scholar
Pulliam, T. & Chaussee, D. 1981 A diagonal form of an implicit approximate-factorizarion algorithm. J. Comput. Phys. 39, 347–363.Google Scholar
Sherer, S. & Scott, J. 2005 High-order compact finite difference methods on overset grids. J. Comput. Phys. 210, 459–496.Google Scholar
Sherer, S. & Visbal, M. 2007 Multi-resolution implicit large eddy simulations using a high-order overset grid approach. Intl J. Numer. Meth. Engng 55, 455–482.Google Scholar
Steger, J. 1978 Implicit finite-difference simulation of flow about arbitrary two-dimensional geometries. AIAA J. 16 (7), 679–686.Google Scholar
Suhs, N., Rogers, S. & Dietz, W.2002 Pegasus 5: an automated pre-processor for overset-grid CFD. AIAA Paper 2002-3186.Google Scholar
Tannehill, J., Anderson, A. & Pletcher, R. 1997 Computational Fluid Mechanics and Heat Transfer. Taylor & Francis.Google Scholar
Tsien, H.-S. 1943 Symmetrical Joukowsky airfoils in shear flow. Q. Appl. Maths 1 (2), 130–148.Google Scholar
Vinokur, M. 1974 Conservation equations of gas dynamics in curvilinear coordinate system. J. Comput. Phys. 14, 105–125.Google Scholar
Visbal, M., Morgan, P. & Rizetta, D.2003 An implicit LES approach based on high-order compact differencing and filtering schemes (invited). AIAA Paper 2003-4098.Google Scholar
Visbal, M. R. & Gaitonde, D. V. 1999 High-order-accurate methods of complex unsteady subsonic flows. AIAA J. 37 (10), 1231–1239.Google Scholar
Visbal, M. R. & Gaitonde, D. V. 2002 On the use of higher-order finite-difference schemes on curvilinear and deforming meshes. J. Comput. Phys. 181, 155–185.Google Scholar
Young, J. & Lai, J. 2004 Oscillation frequency and amplitude effects on the wake of a plunging airfoil. AIAA J. 42 (10), 2042–2052.Google Scholar