Article contents
Linear and nonlinear dynamics of pulsatile channel flow
Published online by Cambridge University Press: 21 February 2017
Abstract
The dynamics of small-amplitude perturbations, as well as the regime of fully developed nonlinear propagating waves, is investigated for pulsatile channel flows. The time-periodic base flows are known analytically and completely determined by the Reynolds number 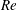 $Re$ (based on the mean flow rate), the Womersley number
$Re$ (based on the mean flow rate), the Womersley number 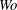 $Wo$ (a dimensionless expression of the frequency) and the flow-rate waveform. This paper considers pulsatile flows with a single oscillating component and hence only three non-dimensional control parameters are present. Linear stability characteristics are obtained both by Floquet analyses and by linearized direct numerical simulations. In particular, the long-term growth or decay rates and the intracyclic modulation amplitudes are systematically computed. At large frequencies (mainly
$Wo$ (a dimensionless expression of the frequency) and the flow-rate waveform. This paper considers pulsatile flows with a single oscillating component and hence only three non-dimensional control parameters are present. Linear stability characteristics are obtained both by Floquet analyses and by linearized direct numerical simulations. In particular, the long-term growth or decay rates and the intracyclic modulation amplitudes are systematically computed. At large frequencies (mainly 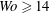 $Wo\geqslant 14$ ), increasing the amplitude of the oscillating component is found to have a stabilizing effect, while it is destabilizing at lower frequencies; strongest destabilization is found for
$Wo\geqslant 14$ ), increasing the amplitude of the oscillating component is found to have a stabilizing effect, while it is destabilizing at lower frequencies; strongest destabilization is found for 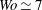 $Wo\simeq 7$ . Whether stable or unstable, perturbations may undergo large-amplitude intracyclic modulations; these intracyclic modulation amplitudes reach huge values at low pulsation frequencies. For linearly unstable configurations, the resulting saturated fully developed finite-amplitude solutions are computed by direct numerical simulations of the complete Navier–Stokes equations. Essentially two types of nonlinear dynamics have been identified: ‘cruising’ regimes for which nonlinearities are sustained throughout the entire pulsation cycle and which may be interpreted as modulated Tollmien–Schlichting waves, and ‘ballistic’ regimes that are propelled into a nonlinear phase before subsiding again to small amplitudes within every pulsation cycle. Cruising regimes are found to prevail for weak base-flow pulsation amplitudes, while ballistic regimes are selected at larger pulsation amplitudes; at larger pulsation frequencies, however, the ballistic regime may be bypassed due to the stabilizing effect of the base-flow pulsating component. By investigating extended regions of a multi-dimensional parameter space and considering both two-dimensional and three-dimensional perturbations, the linear and nonlinear dynamics are systematically explored and characterized.
$Wo\simeq 7$ . Whether stable or unstable, perturbations may undergo large-amplitude intracyclic modulations; these intracyclic modulation amplitudes reach huge values at low pulsation frequencies. For linearly unstable configurations, the resulting saturated fully developed finite-amplitude solutions are computed by direct numerical simulations of the complete Navier–Stokes equations. Essentially two types of nonlinear dynamics have been identified: ‘cruising’ regimes for which nonlinearities are sustained throughout the entire pulsation cycle and which may be interpreted as modulated Tollmien–Schlichting waves, and ‘ballistic’ regimes that are propelled into a nonlinear phase before subsiding again to small amplitudes within every pulsation cycle. Cruising regimes are found to prevail for weak base-flow pulsation amplitudes, while ballistic regimes are selected at larger pulsation amplitudes; at larger pulsation frequencies, however, the ballistic regime may be bypassed due to the stabilizing effect of the base-flow pulsating component. By investigating extended regions of a multi-dimensional parameter space and considering both two-dimensional and three-dimensional perturbations, the linear and nonlinear dynamics are systematically explored and characterized.
Information
- Type
- Papers
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 34
- Cited by


