Hostname: page-component-848d4c4894-p2v8j Total loading time: 0 Render date: 2024-05-09T14:34:58.628Z Has data issue: false hasContentIssue false
  • English
  • Français

Linear and nonlinear responses to harmonic force in rotating flow

Published online by Cambridge University Press:  04 May 2016

Xing Wei
Xing Wei*
Affiliation:
Institute of Natural Sciences, and Department of Physics and Astronomy, Shanghai Jiao Tong University, Shanghai 200240, China Princeton University Observatory, Princeton, NJ 08544, USA
*
†Email address for correspondence: xingwei@astro.princeton.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

For understanding the dissipation in a rotating flow when resonance occurs, we study the rotating flow driven by the harmonic force in a periodic box. Both the linear and nonlinear regimes are studied. The various parameters such as the force amplitude $a$, the force frequency 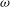${\it\omega}$, the force wavenumber 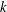$k$ and the Ekman number 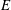$E$ are investigated. In the linear regime, the dissipation at the resonant frequency scales as 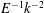$E^{-1}k^{-2}$, and it is much stronger than the dissipation at the non-resonant frequencies on large scales and at low Ekman numbers. In the nonlinear regime, at the resonant frequency the effective dissipation (dissipation normalised with the square of the force amplitude) is lower than in the linear regime and it decreases with increasing force amplitude. This nonlinear suppression effect is significant near the resonant frequency but negligible far away from the resonant frequency. Opposite to the linear regime, in the nonlinear regime at the resonant frequency the lower Ekman number leads to lower dissipation because of the stronger nonlinear effect. This work implies that the previous linear calculations overestimated the tidal dissipation, which is important for understanding the tides in stars and giant planets.

JFM classification

Geophysical and Geological Flows: Geophysical and Geological Flows Geophysical and Geological Flows: Rotating flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 796 , 10 June 2016 , pp. 306 - 317
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Busse, F. H. 1968 Steady fluid flow in a precessing spheroidal shell. J. Fluid Mech. 33, 739–751.CrossRefGoogle Scholar
Cébron, D. & Hollerbach, R. 2014 Tidally driven dynamos in a rotating sphere. Astrophys. J. Lett. 789 (1), L25.CrossRefGoogle Scholar
Cui, Z., Zhang, K. & Liao, X. 2014 On the completeness of inertial wave modes in rotating annular channels. Geophys. Astrophys. Fluid Dyn. 108, 44–59.CrossRefGoogle Scholar
Davidson, P. A. 2014 The dynamics and scaling laws of planetary dynamos driven by inertial waves. Geophys. J. Intl 198, 1832–1847.CrossRefGoogle Scholar
Favier, B., Barker, A. J., Baruteau, C. & Ogilvie, G. I. 2014 Nonlinear evolution of tidally forced inertial waves in rotating fluid bodies. Mon. Not. R. Astron. Soc. 439, 845–860.CrossRefGoogle Scholar
Greenspan, H. P. 1968 Theory of Rotating Fluids. Cambridge University Press.Google Scholar
Hollerbach, R. & Kerswell, R. R. 1995 Oscillatory internal shear layers in rotating and precessing flows. J. Fluid Mech. 298, 327–339.CrossRefGoogle Scholar
Kerswell, R. R. 1993 The instability of precessing flow. Geophys. Astrophys. Fluid Dyn. 72, 107–144.CrossRefGoogle Scholar
Kerswell, R. R. 1994 Tidal excitation of hydromagnetic waves and their damping in the Earth. J. Fluid Mech. 274, 219–241.CrossRefGoogle Scholar
Kumar, P. & Goodman, J. 1996 Nonlinear damping of oscillations in tidal-capture binaries. Astrophys. J. 466, 946–956.CrossRefGoogle Scholar
Lorenzani, S. & Tilgner, A. 2001 Fluid instabilities in precessing spheroidal cavities. J. Fluid Mech. 447, 111–128.CrossRefGoogle Scholar
Lorenzani, S. & Tilgner, A. 2003 Inertial instabilities of fluid flow in precessing spheroidal shells. J. Fluid Mech. 492, 363–379.CrossRefGoogle Scholar
Moffatt, H. K. 1970a Turbulent dynamo action at low magnetic Reynolds number. J. Fluid Mech. 41, 435–452.CrossRefGoogle Scholar
Moffatt, H. K. 1970b Dynamo action associated with random inertial waves in a rotating conducting fluid. J. Fluid Mech. 44, 705–719.CrossRefGoogle Scholar
Ogilvie, G. I. 2005 Wave attractors and the asymptotic dissipation rate of tidal disturbances. J. Fluid Mech. 543, 19–44.CrossRefGoogle Scholar
Ogilvie, G. I. 2014 Tidal dissipation in stars and giant planets. Annu. Rev. Astron. Astrophys. 52, 171–210.CrossRefGoogle Scholar
Rieutord, M. & Valdettaro, L. 1997 Inertial waves in a rotating spherical shell. J. Fluid Mech. 341, 77–99.CrossRefGoogle Scholar
Souchay, J., Mathis, S. & Tokieda, T. 2013 Tides in Astronomy and Astrophysics. Springer.CrossRefGoogle Scholar
Tilgner, A. 2007a Zonal wind driven by inertial modes. Phys. Rev. Lett. 99, 194501.CrossRefGoogle ScholarPubMed
Tilgner, A. 2007b Rotational dynamics of the core. In Treatise on Geophysics (ed. Schubert, G.), chap. 8, pp. 208–243. Elsevier.Google Scholar
Waleffe, F. 1992 The nature of triad interactions in homogeneous turbulence. Phys. Fluids A 4, 350–363.CrossRefGoogle Scholar
Wei, X. 2014 Kinematic dynamo induced by helical waves. Geophys. Astrophys. Fluid Dyn. 109, 159–167.CrossRefGoogle Scholar
Zhang, K., Chan, K. & Liao, X. 2014 On precessing flow in an oblate spheroid of arbitrary eccentricity. J. Fluid Mech. 743, 358–384.CrossRefGoogle Scholar