Article contents
Linear instability of a supersonic boundary layer over a rotating cone
Published online by Cambridge University Press: 18 January 2023
Abstract
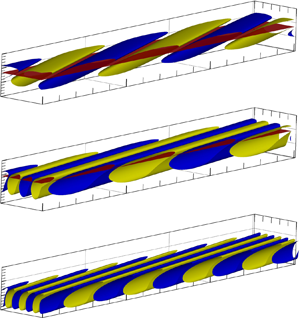
In this paper, we conduct a systematic study of the instability of a boundary layer over a rotating cone that is inserting into a supersonic stream with zero angle of attack. The base flow is obtained by solving the compressible boundary-layer equations using a marching scheme, whose accuracy is confirmed by comparing with the full Navier–Stokes solution. Setting the oncoming Mach number and the semi-apex angle to be 3 and 7 $^\circ$, respectively, the instability characteristics for different rotating rates (
$^\circ$, respectively, the instability characteristics for different rotating rates ( $\bar \varOmega$, defined as the ratio of the rotating speed of the cone to the axial velocity) and Reynolds numbers (
$\bar \varOmega$, defined as the ratio of the rotating speed of the cone to the axial velocity) and Reynolds numbers ( $R$) are revealed. For a rather weak rotation,
$R$) are revealed. For a rather weak rotation,  $\bar \varOmega \ll 1$, only the modified Mack mode (MMM) exists, which is an extension of the supersonic Mack mode in a quasi-two-dimensional boundary layer to a rotation configuration. Further increase of
$\bar \varOmega \ll 1$, only the modified Mack mode (MMM) exists, which is an extension of the supersonic Mack mode in a quasi-two-dimensional boundary layer to a rotation configuration. Further increase of  $\bar \varOmega$ leads to the appearance of a cross-flow mode (CFM), coexisting with the MMM but in the quasi-zero frequency band. The unstable zones of the MMM and CFM merge together, and so they are referred to as the type-I instability. When
$\bar \varOmega$ leads to the appearance of a cross-flow mode (CFM), coexisting with the MMM but in the quasi-zero frequency band. The unstable zones of the MMM and CFM merge together, and so they are referred to as the type-I instability. When  $\bar \varOmega$ is increased to an
$\bar \varOmega$ is increased to an  $O(1)$ level, an additional unstable zone emerges, which is referred to as the type-II instability to be distinguished from the aforementioned type-I instability. The type-II instability appears as a centrifugal mode (CM) when
$O(1)$ level, an additional unstable zone emerges, which is referred to as the type-II instability to be distinguished from the aforementioned type-I instability. The type-II instability appears as a centrifugal mode (CM) when  $R$ is less than a certain value, but appears as a new CFM for higher Reynolds numbers. The unstable zone of the type-II CM enlarges as
$R$ is less than a certain value, but appears as a new CFM for higher Reynolds numbers. The unstable zone of the type-II CM enlarges as  $\bar \varOmega$ increases. The vortex structures of these types of instability modes are compared, and their large-
$\bar \varOmega$ increases. The vortex structures of these types of instability modes are compared, and their large- $R$ behaviours are also discussed.
$R$ behaviours are also discussed.
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
References
REFERENCES
- 4
- Cited by


