Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Araya, Guillermo G.
2016.
Shedding Light into the Quasi-Laminarization Process.
Castillo, Luciano
and
Hussain, Fazle
2017.
The logarithmic and power law behaviors of the accelerating, turbulent thermal boundary layer.
Physics of Fluids,
Vol. 29,
Issue. 2,
Wu, Xiaohua
2017.
Inflow Turbulence Generation Methods.
Annual Review of Fluid Mechanics,
Vol. 49,
Issue. 1,
p.
23.
Ranjan, Rajesh
and
Narasimha, Roddam
2017.
An Assessment of the Two-Layer Quasi-Laminar Theory of Relaminarization Through Recent High-Re Accelerated Turbulent Boundary Layer Experiments.
Journal of Fluids Engineering,
Vol. 139,
Issue. 11,
Wang, Jianjie
Pan, Chong
Zhang, Qingsong
and
Li, Tian
2018.
Modulating the Near-Wall Velocity Fields in Wall-Bounded Turbulence via Discrete Surface Roughness.
AIAA Journal,
Vol. 56,
Issue. 7,
p.
2642.
Araya, G.
and
Rodriguez, D.
2018.
Visualization and assessment of turbulent coherent structures in laminarescent boundary layers.
Journal of Visualization,
Vol. 21,
Issue. 2,
p.
191.
Deng, Sichao
Pan, Chong
Wang, Jinjun
and
He, Guosheng
2018.
On the spatial organization of hairpin packets in a turbulent boundary layer at low-to-moderate Reynolds number.
Journal of Fluid Mechanics,
Vol. 844,
Issue. ,
p.
635.
Araya, G.
and
Torres, G.
2019.
Structural Reynolds analogy in laminarescent boundary layers via DNS.
Journal of Visualization,
Vol. 22,
Issue. 3,
p.
529.
Araya, Guillermo
Marin, Guillermo
Cucchietti, Fernando
Meta, Irene
and
Grima, Rogeli
2019.
High Performance Computing.
Vol. 979,
Issue. ,
p.
174.
Araya, Guillermo
Lagares, Christian
and
Jansen, Kenneth E.
2020.
Reynolds number dependency in supersonic spatially-developing turbulent boundary layers.
Zhao, Yaomin
and
Sandberg, Richard D.
2020.
Bypass transition in boundary layers subject to strong pressure gradient and curvature effects.
Journal of Fluid Mechanics,
Vol. 888,
Issue. ,
Saltar, German
and
Araya, Guillermo
2020.
Reynolds shear stress modeling in turbulent boundary layers subject to very strong favorable pressure gradient.
Computers & Fluids,
Vol. 202,
Issue. ,
p.
104494.
Lagares, Christian J.
and
Araya, Guillermo
2021.
Compressibility Effects on High-Reynolds Coherent Structures via Two-Point Correlations.
Araya, Guillermo
Lagares, Christian J.
Santiago, Jean
and
Jansen, Kenneth E.
2021.
Wall temperature effect on hypersonic turbulent boundary layers via DNS.
Paeres, David
Santiago, Jean
Lagares, Christian J.
Rivera, Wilson
Craig, Alan B.
and
Araya, Guillermo
2021.
Design of a Virtual Wind Tunnel for CFD Visualization.
Wang, Xinwei
Wang, Yufei
Tian, Haiping
and
Jiang, Nan
2021.
Effects of the slip wall on the drag and coherent structures of turbulent boundary layer.
Acta Mechanica Sinica,
Vol. 37,
Issue. 8,
p.
1278.
Devenport, William J.
and
Lowe, K. Todd
2022.
Equilibrium and non-equilibrium turbulent boundary layers.
Progress in Aerospace Sciences,
Vol. 131,
Issue. ,
p.
100807.
Pozuelo, Ramón
Li, Qiang
Schlatter, Philipp
and
Vinuesa, Ricardo
2022.
An adverse-pressure-gradient turbulent boundary layer with nearly constant up to .
Journal of Fluid Mechanics,
Vol. 939,
Issue. ,
ICHIMIYA, Masashi
NAKAMURA, Ikuo
and
NAKATA, Masaki
2022.
Relaminarization of accelerated turbulent boundary layer under favorable pressure gradient with sink flow type (Coherent structure and two-point statistics).
Transactions of the JSME (in Japanese),
Vol. 88,
Issue. 909,
p.
22-00010.
Lagares, Christian J.
and
Araya, Guillermo
2022.
Power spectrum analysis in supersonic/hypersonic turbulent boundary layers.
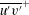 $\overline{u^{\prime }v^{\prime }}^{+}$ , monotonically decreases downstream and exhibits a logarithmic behaviour (e.g.
$\overline{u^{\prime }v^{\prime }}^{+}$ , monotonically decreases downstream and exhibits a logarithmic behaviour (e.g. 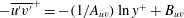 $-\overline{u^{\prime }v^{\prime }}^{+}=-(1/A_{uv})\ln y^{+}+B_{uv}$ ) in the mesolayer region (e.g.
$-\overline{u^{\prime }v^{\prime }}^{+}=-(1/A_{uv})\ln y^{+}+B_{uv}$ ) in the mesolayer region (e.g. 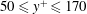 $50\leqslant y^{+}\leqslant 170$ ). The thickness of the log layer of
$50\leqslant y^{+}\leqslant 170$ ). The thickness of the log layer of 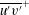 $\overline{u^{\prime }v^{\prime }}^{+}$ increases with the streamwise distance and with the pressure gradient strength, extending over a large portion of the TBL thickness (up to 55 %). Simulations reveal that
$\overline{u^{\prime }v^{\prime }}^{+}$ increases with the streamwise distance and with the pressure gradient strength, extending over a large portion of the TBL thickness (up to 55 %). Simulations reveal that 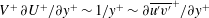 $V^{+}\,\partial U^{+}/\partial y^{+}\sim 1/y^{+}\sim \partial \overline{u^{\prime }v^{\prime }}^{+}/\partial y^{+}$ , resulting in a logarithmic
$V^{+}\,\partial U^{+}/\partial y^{+}\sim 1/y^{+}\sim \partial \overline{u^{\prime }v^{\prime }}^{+}/\partial y^{+}$ , resulting in a logarithmic 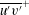 $\overline{u^{\prime }v^{\prime }}^{+}$ profile. Also,
$\overline{u^{\prime }v^{\prime }}^{+}$ profile. Also, 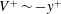 $V^{+}\sim -y^{+}$ is no longer negligible as in zero-pressure-gradient (ZPG) flows. Other experimental/numerical data at similar favourable-pressure-gradient (FPG) strengths also show the presence of a log region in
$V^{+}\sim -y^{+}$ is no longer negligible as in zero-pressure-gradient (ZPG) flows. Other experimental/numerical data at similar favourable-pressure-gradient (FPG) strengths also show the presence of a log region in 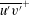 $\overline{u^{\prime }v^{\prime }}^{+}$ . This log region in
$\overline{u^{\prime }v^{\prime }}^{+}$ . This log region in  $\overline{u^{\prime }v^{\prime }}^{+}$ is larger in sink flows than in other spatially developing FPG flows. The latter flows exhibit the presence of a small power-law region in
$\overline{u^{\prime }v^{\prime }}^{+}$ is larger in sink flows than in other spatially developing FPG flows. The latter flows exhibit the presence of a small power-law region in 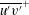 $\overline{u^{\prime }v^{\prime }}^{+}$ , which is non-existent in sink flows.
$\overline{u^{\prime }v^{\prime }}^{+}$ , which is non-existent in sink flows.

