Hostname: page-component-8448b6f56d-xtgtn Total loading time: 0 Render date: 2024-04-24T15:08:54.364Z Has data issue: false hasContentIssue false
  • English
  • Français

Long frontal waves and dynamic scaling in freely evolving equivalent barotropic flow

Published online by Cambridge University Press:  18 March 2019

B. H. Burgess Open the ORCID record for B. H. Burgess [Opens in a new window]  and
D. G. Dritschel Open the ORCID record for D. G. Dritschel [Opens in a new window]
B. H. Burgess*
Affiliation:
School of Mathematics and Statistics, University of St Andrews, St Andrews KY16 9SS, UK
D. G. Dritschel
Affiliation:
School of Mathematics and Statistics, University of St Andrews, St Andrews KY16 9SS, UK
*
†Email address for correspondence: bhb3@st-andrews.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

We present a scaling theory that links the frequency of long frontal waves to the kinetic energy decay rate and inverse transfer of potential energy in freely evolving equivalent barotropic turbulence. The flow energy is predominantly potential, and the streamfunction makes the dominant contribution to potential vorticity (PV) over most of the domain, except near PV fronts of width $O(L_{D})$, where 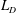$L_{D}$ is the Rossby deformation length. These fronts bound large vortices within which PV is well-mixed and arranged into a staircase structure. The jets collocated with the fronts support long-wave undulations, which facilitate collisions and mergers between the mixed regions, implicating the frontal dynamics in the growth of potential-energy-containing flow features. Assuming the mixed regions grow self-similarly in time and using the dispersion relation for long frontal waves (Nycander et al., Phys. Fluids A, vol. 5, 1993, pp. 1089–1091) we predict that the total frontal length and kinetic energy decay like 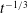$t^{-1/3}$, while the length scale of the staircase vortices grows like 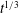$t^{1/3}$. High-resolution simulations confirm our predictions.

JFM classification

Geophysical and Geological Flows: Quasi-geostrophic flows Vortex Flows: Vortex dynamics
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 866 , 10 May 2019 , R3
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arbic, B. K. & Flierl, G. R. 2003 Coherent vortices and kinetic energy ribbons in asymptotic, quasi two-dimensional f-plane turbulence. Phys. Fluids 15, 2177–2189.Google Scholar
Boffetta, G., De Lillo, F. & Musacchio, S. 2002 Inverse cascade in Charney–Hasegawa–Mima turbulence. Europhys. Lett. 59, 687–693.Google Scholar
Burgess, B. H., Dritschel, D. G. & Scott, R. K. 2017 Extended scale invariance in the vortices of freely evolving two-dimensional turbulence. Phys. Rev. Fluids 2, 114702.Google Scholar
Dritschel, D. G. & Fontane, J. 2010 The combined Lagrangian advection method. J. Comput. Phys. 229, 5408–5417.Google Scholar
Dritschel, D. G. & McIntyre, M. E. 2008 Multiple jets as PV staircases: the Phillips effect and the resilience of eddy-transport barriers. J. Atmos. Sci. 65, 855–874.Google Scholar
Dritschel, D. G. & Scott, R. K. 2011 Jet sharpening by turbulent mixing. Phil. Trans. R. Soc. Lond. 369, 754–770.Google Scholar
Dritschel, D. G., Scott, R. K., Macaskill, C., Gottwald, G. A. & Tran, C. V. 2008 Unifying scaling theory for vortex dynamics in two-dimensional turbulence. Phys. Rev. Lett. 101, 094501.Google Scholar
Dunkerton, T. J. & Scott, R. K. 2008 A barotropic model of the angular momentum-conserving potential vorticity staircase in spherical geometry. J. Atmos. Sci. 65, 1105–1136.Google Scholar
Hasegawa, A. & Mima, K. 1978 Pseudo-three-dimensional turbulence in a magnetized nonuniform plasma. Phys. Fluids 21, 87–92.Google Scholar
Iwayama, T., Shepherd, T. G. & Watanabe, T. 2002 An ‘ideal’ form of decaying two-dimensional turbulence. J. Fluid Mech. 456, 183–198.Google Scholar
Larichev, V. D. & McWilliams, J. C. 1991 Weakly decaying turbulence in an equivalent barotropic fluid. Phys. Fluids A 3, 938–950.Google Scholar
McIntyre, M. E. 1982 How well do we understand the dynamics of stratospheric warmings? J. Met. Soc. Japan 60, 37–65.Google Scholar
Nycander, J., Dritschel, D. G. & Sutyrin, G. G. 1993 The dynamics of long frontal waves in the shallow-water equations. Phys. Fluids A 5, 1089–1091.Google Scholar
Pedlosky, J. 1987 Geophysical Fluid Dynamics, 2nd edn. Springer.Google Scholar
Płotka, H. & Dritschel, D. G. 2012 Quasi-geostrophic shallow-water vortex-patch equilibria and their stability. Geophys. Astrophys. Fluid Dyn. 106, 574–595.Google Scholar
Scott, R. K. & Dritschel, D. G. 2018 Zonal jet formation by potential vorticity mixing at large and small scales. In Zonal Jets (ed. Galperin, B. & Read, P. L.), Cambridge University Press.Google Scholar
Tran, C. V. & Dritschel, D. G. 2006 Impeded inverse energy transfer in the Charney–Hasegawa–Mima model of quasi-geostrophic flows. J. Fluid Mech. 551, 435–443.Google Scholar

Burgess and Dritschel supplementary movie 1

Kinetic energy density field at times $t = 110 \ 000 - 190 \ 000$.

Download Burgess and Dritschel supplementary movie 1(Video)
Video 9.3 MB

Burgess and Dritschel supplementary movie 2

Potential vorticity field at times $t = 110 \ 000 - 190 \ 000$.

Download Burgess and Dritschel supplementary movie 2(Video)
Video 2.1 MB