Article contents
Manning’s formula and Strickler’s scaling explained by a co-spectral budget model
Published online by Cambridge University Press: 12 January 2017
Abstract
Manning’s empirical formula in conjunction with Strickler’s scaling is widely used to predict the bulk velocity 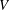 $V$ from the hydraulic radius
$V$ from the hydraulic radius 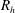 $R_{h}$ , the roughness size
$R_{h}$ , the roughness size  $r$ and the slope of the energy grade line
$r$ and the slope of the energy grade line 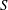 $S$ in uniform channel and pipe flows at high bulk Reynolds numbers. Despite their importance in science and engineering, both Manning’s and Strickler’s formulations have waited for decades before finding a theoretical explanation. This was provided, for the first time, by Gioia & Bombardelli (Phys. Rev. Lett., vol. 88, 2002, 014501), labelled as GB02, using phenomenological arguments. Perhaps their most remarkable finding was the link between the Strickler and the Kolmogorov scaling exponents, the latter pertaining to velocity fluctuations in the inertial subrange of the turbulence spectrum and presumed to be universal. In this work, the GB02 analysis is first revisited, showing that GB02 employed several ad hoc scaling assumptions for the turbulent kinetic energy dissipation rate and, although implicitly, for the mean velocity gradient adjacent to the roughness elements. The similarity constants arising from the GB02 scaling assumptions were presumed to be independent of
$S$ in uniform channel and pipe flows at high bulk Reynolds numbers. Despite their importance in science and engineering, both Manning’s and Strickler’s formulations have waited for decades before finding a theoretical explanation. This was provided, for the first time, by Gioia & Bombardelli (Phys. Rev. Lett., vol. 88, 2002, 014501), labelled as GB02, using phenomenological arguments. Perhaps their most remarkable finding was the link between the Strickler and the Kolmogorov scaling exponents, the latter pertaining to velocity fluctuations in the inertial subrange of the turbulence spectrum and presumed to be universal. In this work, the GB02 analysis is first revisited, showing that GB02 employed several ad hoc scaling assumptions for the turbulent kinetic energy dissipation rate and, although implicitly, for the mean velocity gradient adjacent to the roughness elements. The similarity constants arising from the GB02 scaling assumptions were presumed to be independent of 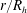 $r/R_{h}$ , which is inconsistent with well-known flow properties in the near-wall region of turbulent wall flows. Because of the dependence of these similarity constants on
$r/R_{h}$ , which is inconsistent with well-known flow properties in the near-wall region of turbulent wall flows. Because of the dependence of these similarity constants on 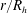 $r/R_{h}$ , this existing theory requires the validity of the Strickler scaling to cancel the dependence of these constants on
$r/R_{h}$ , this existing theory requires the validity of the Strickler scaling to cancel the dependence of these constants on 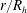 $r/R_{h}$ so as to arrive at the Strickler scaling and Manning’s formula. Here, the GB02 approach is corroborated using a co-spectral budget (CSB) model for the wall shear stress formulated at the cross-over between the roughness sublayer and the log region. Assuming a simplified shape for the spectrum of the vertical velocity
$r/R_{h}$ so as to arrive at the Strickler scaling and Manning’s formula. Here, the GB02 approach is corroborated using a co-spectral budget (CSB) model for the wall shear stress formulated at the cross-over between the roughness sublayer and the log region. Assuming a simplified shape for the spectrum of the vertical velocity 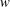 $w$ , the proposed CSB model (subject to another simplifying assumption that production is balanced by pressure–velocity interaction) allows Manning’s formula to be derived. To substantiate this approach, numerical solutions to the CSB over the entire flow depth using different spectral shapes for
$w$ , the proposed CSB model (subject to another simplifying assumption that production is balanced by pressure–velocity interaction) allows Manning’s formula to be derived. To substantiate this approach, numerical solutions to the CSB over the entire flow depth using different spectral shapes for 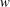 $w$ are carried out for a wide range of
$w$ are carried out for a wide range of 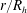 $r/R_{h}$ . The results from this analysis support the simplifying hypotheses used to derive Manning’s equation. The derived equation provides a formulation for
$r/R_{h}$ . The results from this analysis support the simplifying hypotheses used to derive Manning’s equation. The derived equation provides a formulation for  $n$ that agrees with reported values in the literature over seven decades of
$n$ that agrees with reported values in the literature over seven decades of  $r$ variations. While none of the investigated spectral shapes allows the recovery of the Strickler scaling, the numerical solutions of the CSB reproduce the Nikuradse data in the fully rough regime, thereby confirming that the Strickler scaling represents only an approximate fit for the friction factor for granular roughness.
$r$ variations. While none of the investigated spectral shapes allows the recovery of the Strickler scaling, the numerical solutions of the CSB reproduce the Nikuradse data in the fully rough regime, thereby confirming that the Strickler scaling represents only an approximate fit for the friction factor for granular roughness.
Information
- Type
- Papers
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 43
- Cited by


