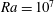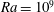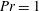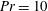1 Introduction
Natural convection is a common and important phenomenon that is omnipresent in Nature. It leads to the transfer of internal energy, within an unstably stratified fluid layer, via a buoyancy-induced flow. Ocean currents, which are driven by gradients in density and salinity (Marshall & Schott Reference Marshall and Schott1999; Wirth & Barnier Reference Wirth and Barnier2006), and the mantle convection inside the Earth, which drives the plate tectonics and generates the geomagnetic field (McKenzie, Roberts & Weiss Reference McKenzie, Roberts and Weiss1974; Glatzmaier & Roberts Reference Glatzmaier and Roberts1995), are two examples of natural convection. Even outside of our planet, at the most distant stars, convection is of tremendous importance (Spiegel Reference Spiegel1971; Cattaneo, Emonet & Weiss Reference Cattaneo, Emonet and Weiss2003).
An idealized system that is commonly used to study natural convection, as it is mathematically well defined and can be reproduced in a laboratory experiment, is Rayleigh–Bénard (RB) convection (Normand, Pomeau & Velarde Reference Normand, Pomeau and Velarde1977; Ahlers, Grossmann & Lohse Reference Ahlers, Grossmann and Lohse2009; Lohse & Xia Reference Lohse and Xia2010; Chillà & Schumacher Reference Chillà and Schumacher2012). The RB system consists of a fluid in a container, which is heated from below and cooled from above. The fluid is subject to an external gravitational field
![]() $g$
. Apart from the geometric ones, this system has two non-dimensional control parameters, namely the Rayleigh number
$g$
. Apart from the geometric ones, this system has two non-dimensional control parameters, namely the Rayleigh number
![]() $Ra=\unicode[STIX]{x1D6FD}g\unicode[STIX]{x0394}H^{3}/\unicode[STIX]{x1D708}\unicode[STIX]{x1D705}$
, which measures the strength of the thermal driving, and the Prandtl number
$Ra=\unicode[STIX]{x1D6FD}g\unicode[STIX]{x0394}H^{3}/\unicode[STIX]{x1D708}\unicode[STIX]{x1D705}$
, which measures the strength of the thermal driving, and the Prandtl number
![]() $\mathit{Pr}=\unicode[STIX]{x1D708}/\unicode[STIX]{x1D705}$
, a property of the fluid, where
$\mathit{Pr}=\unicode[STIX]{x1D708}/\unicode[STIX]{x1D705}$
, a property of the fluid, where
![]() $\unicode[STIX]{x1D6FD}$
and
$\unicode[STIX]{x1D6FD}$
and
![]() $\unicode[STIX]{x1D705}$
are the isobaric thermal expansion and temperature diffusivity coefficients of the fluid,
$\unicode[STIX]{x1D705}$
are the isobaric thermal expansion and temperature diffusivity coefficients of the fluid,
![]() $H$
is the system height,
$H$
is the system height,
![]() $\unicode[STIX]{x1D6E5}$
is the applied temperature difference between the plates, and
$\unicode[STIX]{x1D6E5}$
is the applied temperature difference between the plates, and
![]() $\unicode[STIX]{x1D708}$
is the kinematic viscosity. Depending on the geometry of the system, other control parameters such as the aspect ratio of the system,
$\unicode[STIX]{x1D708}$
is the kinematic viscosity. Depending on the geometry of the system, other control parameters such as the aspect ratio of the system,
![]() $\unicode[STIX]{x1D6E4}=L/H$
, appear, where
$\unicode[STIX]{x1D6E4}=L/H$
, appear, where
![]() $L$
is a characteristic horizontal length of the system.
$L$
is a characteristic horizontal length of the system.
Above a certain critical Rayleigh number, RB flow is linearly unstable, and any perturbation will cause the onset of convection. This critical value is determined by the properties of the fluid and the boundary conditions (BCs) of the RB system. If the thermal driving of the system is far above the critical
![]() $Ra$
, the flow becomes turbulent. This dramatically increases the heat transfer with respect to the purely conductive case. Modelling this heat transfer is essential for understanding what is going on inside stars, the Earth’s mantle and many other systems. RB experiments (and simulations) typically consist of a bottom and a top plate, which have homogeneous BCs, and lateral BCs, which are either periodic (simulations) to mimic laterally unconfined systems or adiabatic (experiments) to account for a lateral confinement that minimizes the heat losses.
$Ra$
, the flow becomes turbulent. This dramatically increases the heat transfer with respect to the purely conductive case. Modelling this heat transfer is essential for understanding what is going on inside stars, the Earth’s mantle and many other systems. RB experiments (and simulations) typically consist of a bottom and a top plate, which have homogeneous BCs, and lateral BCs, which are either periodic (simulations) to mimic laterally unconfined systems or adiabatic (experiments) to account for a lateral confinement that minimizes the heat losses.
However, these idealized systems assume that both the top and bottom plates have perfectly homogeneous conducting surfaces, while for all real physical systems, there is a certain degree of imperfection. In Nature we see such inhomogeneities; for example, the fractures in ice floes (Marcq & Weiss Reference Marcq and Weiss2012) or the much-debated insulating effects of continents on mantle convection (Lenardic et al.
Reference Lenardic, Moresi, Jellinek and Manga2005). Other examples include convection over mixed (agricultural) vegetation and cities (Zhao et al.
Reference Zhao, Lee, Smith and Oleson2014). In engineering applications, or in RB experiments, these can be small defects in or dirt on the conducting plates, which could result in lower-than-optimal heat transport. The limiting cases of the BCs are constant-heat-flux BCs, constant-temperature BCs or thermally insulating BCs with no heat flux. The difference in heat transfer between the first two types of BCs, Dirichlet and von Neumann, was found to be negligible for direct numerical simulations (DNS) at large
![]() $Ra$
(Johnston & Doering Reference Johnston and Doering2007, Reference Johnston and Doering2009; Stevens, Lohse & Verzicco Reference Stevens, Lohse and Verzicco2011), but the increase in flow strength under fixed-temperature BCs cannot be neglected (Huang et al.
Reference Huang, Wang, Xi and Xia2015). Accounting for a finite conductivity of the thermal sources can lead to significant reduction in the heat transport (Verzicco Reference Verzicco2004).
$Ra$
(Johnston & Doering Reference Johnston and Doering2007, Reference Johnston and Doering2009; Stevens, Lohse & Verzicco Reference Stevens, Lohse and Verzicco2011), but the increase in flow strength under fixed-temperature BCs cannot be neglected (Huang et al.
Reference Huang, Wang, Xi and Xia2015). Accounting for a finite conductivity of the thermal sources can lead to significant reduction in the heat transport (Verzicco Reference Verzicco2004).
Temperature BCs can also be spatially and temporally varying. The study of the effects of these imperfect BCs goes back to Kelly & Pal (Reference Kelly and Pal1978) and later Yoo & Moon (Reference Yoo and Moon1991), who applied sinusoidal temperature BCs on both plates, which mimic plates with embedded heaters. These plates are locally hotter, when closer to the heater elements. Jin & Xia (Reference Jin and Xia2008) showed that the Nusselt number is increased when the energy input into the system from the plates is periodically pulsed instead of stationary. Recent experiments from Wang, Huang & Xia (Reference Wang, Huang and Xia2017) using insulating lids at the top boundary of an RB cell showed that, with increasing insulating fraction, the same amount of heat goes through a smaller cooling area. Some simulations of inhomogeneous BCs have also been performed. Cooper, Moresi & Lenardic (Reference Cooper, Moresi and Lenardic2013) simulated two- (2D) and three-dimensional (3D) RB systems of mixed adiabatic–conducting BCs at one plate at moderate Rayleigh numbers, with a geophysical focus, finding that the distribution of the patches caused changes in the flow configuration, the bulk temperature and the Nusselt number. The simulations by Ripesi et al. (Reference Ripesi, Bigerale, Sbragaglia and Wirth2014) added non-conducting defects in the form of periodic patches to the top plate of a 2D numerical RB system, and studied both the transition to turbulence of RB flow, finding a delay in this transition when defects were present, and the fully turbulent regime, finding a decrease in Nusselt number when the patch wavelength was larger than the characteristic thermal boundary layer scale.
Here, we extend the research of Ripesi et al. (Reference Ripesi, Bigerale, Sbragaglia and Wirth2014) by applying non-conducting stripe patterns to a 3D RB system. We will focus on the fully turbulent regime instead of the transition to turbulence, and consider a wider range of patterns at higher
![]() $Ra$
, extending the work by Cooper et al. (Reference Cooper, Moresi and Lenardic2013). We start by applying distributions of striped insulating patterns to the top boundary only, and study the dependence of both local and global variables, e.g. effective heat transfer and average bulk temperature, on the number of stripes. For most of the study, we keep the conducting and insulating areas equal to each other, but the effect of the ratio of these areas is also studied, which mimics the degree of imperfection and pollution on the plates. We also study the effect of applying the same pattern to both plates and the role of the pattern geometry by applying a 2D chequerboard insulating–conducting pattern on the top plate. Chequerboards and stripes can be seen as the two limiting cases for the pattern geometry.
$Ra$
, extending the work by Cooper et al. (Reference Cooper, Moresi and Lenardic2013). We start by applying distributions of striped insulating patterns to the top boundary only, and study the dependence of both local and global variables, e.g. effective heat transfer and average bulk temperature, on the number of stripes. For most of the study, we keep the conducting and insulating areas equal to each other, but the effect of the ratio of these areas is also studied, which mimics the degree of imperfection and pollution on the plates. We also study the effect of applying the same pattern to both plates and the role of the pattern geometry by applying a 2D chequerboard insulating–conducting pattern on the top plate. Chequerboards and stripes can be seen as the two limiting cases for the pattern geometry.
This paper is organized as follows. First, in § 2 we detail the geometry and numerical method. In the next section, the results for the stripe pattern variations will be discussed, where both conducting and insulating areas are kept constant. This is first done on the top plate and later the pattern is applied on both plates. A Fourier analysis was performed to study the penetration depth of the pattern imprint in the flow. In § 3.2 a pattern is added to both plates, in § 3.3, we present and discuss the results for varying the ratio of conducting to insulating surface while keeping the number of divisions constant, and in § 3.4 we present the results for a plate with a chequerboard pattern instead of a striped pattern. The paper is concluded by presenting the conclusions and outlook in § 4.
2 Numerical method
In this numerical study, we solve the incompressible Navier–Stokes equations within the Boussinesq approximation for RB. In non-dimensional form, these read
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}{\displaystyle \frac{\text{D}\boldsymbol{u}}{\text{D}t}}=-\unicode[STIX]{x1D735}P+\left({\displaystyle \frac{\mathit{Pr}}{Ra}}\right)^{1/2}\unicode[STIX]{x1D6FB}^{2}\boldsymbol{u}+\unicode[STIX]{x1D703}\hat{\boldsymbol{z}},\\ {\displaystyle \frac{\text{D}\unicode[STIX]{x1D703}}{\text{D}t}}={\displaystyle \frac{1}{\left(\mathit{Pr}Ra\right)^{1/2}}}\unicode[STIX]{x1D6FB}^{2}\unicode[STIX]{x1D703},\\ \unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}=0,\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}{\displaystyle \frac{\text{D}\boldsymbol{u}}{\text{D}t}}=-\unicode[STIX]{x1D735}P+\left({\displaystyle \frac{\mathit{Pr}}{Ra}}\right)^{1/2}\unicode[STIX]{x1D6FB}^{2}\boldsymbol{u}+\unicode[STIX]{x1D703}\hat{\boldsymbol{z}},\\ {\displaystyle \frac{\text{D}\unicode[STIX]{x1D703}}{\text{D}t}}={\displaystyle \frac{1}{\left(\mathit{Pr}Ra\right)^{1/2}}}\unicode[STIX]{x1D6FB}^{2}\unicode[STIX]{x1D703},\\ \unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}=0,\end{array}\right\}\end{eqnarray}$$
where
![]() $u$
is the non-dimensional velocity,
$u$
is the non-dimensional velocity,
![]() $P$
is the non-dimensional pressure,
$P$
is the non-dimensional pressure,
![]() $\unicode[STIX]{x1D703}$
is the non-dimensional temperature and
$\unicode[STIX]{x1D703}$
is the non-dimensional temperature and
![]() $\hat{\boldsymbol{z}}$
is the unit vector pointing in the direction opposite to gravity
$\hat{\boldsymbol{z}}$
is the unit vector pointing in the direction opposite to gravity
![]() $g$
. For non-dimensionalization, the temperature scale is the temperature difference between the plates
$g$
. For non-dimensionalization, the temperature scale is the temperature difference between the plates
![]() $\unicode[STIX]{x1D6E5}$
, the length scale their distance
$\unicode[STIX]{x1D6E5}$
, the length scale their distance
![]() $H$
and the velocity scale is the free-fall velocity
$H$
and the velocity scale is the free-fall velocity
![]() $U_{f}=\sqrt{g\unicode[STIX]{x1D6FD}\unicode[STIX]{x0394}H}$
.
$U_{f}=\sqrt{g\unicode[STIX]{x1D6FD}\unicode[STIX]{x0394}H}$
.
We consider a geometry that is a horizontally doubly periodic cuboid. The domain has horizontal periodicity lengths of
![]() $L_{x}$
and
$L_{x}$
and
![]() $L_{y}$
, and a vertical dimension
$L_{y}$
, and a vertical dimension
![]() $H$
. These variables with a tilde superscript denote their non-dimensional counterparts. The equations were discretized using an energy-conserving second-order finite-difference scheme, and a fractional time step for time marching using a third-order low-storage Runge–Kutta scheme for the nonlinear terms, and a second-order Adams–Bashforth scheme for all viscous and conducting terms (Verzicco & Orlandi Reference Verzicco and Orlandi1996; van der Poel et al.
Reference van der Poel, Ostilla-Monico, Donners and Verzicco2015). The code was heavily parallelized to run on hundreds or even thousands of cores simultaneously and was validated many times (Stevens, Verzicco & Lohse Reference Stevens, Verzicco and Lohse2010; Stevens et al.
Reference Stevens, Lohse and Verzicco2011; van der Poel et al.
Reference van der Poel, Ostilla-Monico, Donners and Verzicco2015). Recently, the code was open-sourced and is available for download at www.AFiD.eu.
$H$
. These variables with a tilde superscript denote their non-dimensional counterparts. The equations were discretized using an energy-conserving second-order finite-difference scheme, and a fractional time step for time marching using a third-order low-storage Runge–Kutta scheme for the nonlinear terms, and a second-order Adams–Bashforth scheme for all viscous and conducting terms (Verzicco & Orlandi Reference Verzicco and Orlandi1996; van der Poel et al.
Reference van der Poel, Ostilla-Monico, Donners and Verzicco2015). The code was heavily parallelized to run on hundreds or even thousands of cores simultaneously and was validated many times (Stevens, Verzicco & Lohse Reference Stevens, Verzicco and Lohse2010; Stevens et al.
Reference Stevens, Lohse and Verzicco2011; van der Poel et al.
Reference van der Poel, Ostilla-Monico, Donners and Verzicco2015). Recently, the code was open-sourced and is available for download at www.AFiD.eu.
The domain was discretized by
![]() $n_{x}\times n_{y}\times n_{z}=360\times 360\times 288$
grid points. In both horizontal directions, the grid was uniformly divided, and in the vertical direction the points were clustered near the top and bottom plates. A number of simulations were conducted to test the aspect ratio dependence and the grid independence. These tests did not show any significant differences in the range of Rayleigh numbers used in this study. For RB convection, a series of exact relationships that link the Nusselt number to the global kinetic energy dissipation (
$n_{x}\times n_{y}\times n_{z}=360\times 360\times 288$
grid points. In both horizontal directions, the grid was uniformly divided, and in the vertical direction the points were clustered near the top and bottom plates. A number of simulations were conducted to test the aspect ratio dependence and the grid independence. These tests did not show any significant differences in the range of Rayleigh numbers used in this study. For RB convection, a series of exact relationships that link the Nusselt number to the global kinetic energy dissipation (
![]() $\unicode[STIX]{x1D708}\unicode[STIX]{x1D6FB}^{2}u$
) and the thermal dissipation (
$\unicode[STIX]{x1D708}\unicode[STIX]{x1D6FB}^{2}u$
) and the thermal dissipation (
![]() $\unicode[STIX]{x1D705}\unicode[STIX]{x1D6FB}^{2}\unicode[STIX]{x1D703}$
) exist (Shraiman & Siggia Reference Shraiman and Siggia1990; Ahlers et al.
Reference Ahlers, Grossmann and Lohse2009), and they have been further used to check the spatial accuracy of the simulation as in Stevens et al. (Reference Stevens, Verzicco and Lohse2010). The size of the time steps was chosen dynamically by imposing that the Courant–Friedrichs–Lewy (CFL) number in the grid would not exceed
$\unicode[STIX]{x1D705}\unicode[STIX]{x1D6FB}^{2}\unicode[STIX]{x1D703}$
) exist (Shraiman & Siggia Reference Shraiman and Siggia1990; Ahlers et al.
Reference Ahlers, Grossmann and Lohse2009), and they have been further used to check the spatial accuracy of the simulation as in Stevens et al. (Reference Stevens, Verzicco and Lohse2010). The size of the time steps was chosen dynamically by imposing that the Courant–Friedrichs–Lewy (CFL) number in the grid would not exceed
![]() $1.2$
.
$1.2$
.
The main response of the system is the Nusselt number (
![]() $Nu$
), which is the heat transfer non-dimensionalized using the purely conductive heat transfer:
$Nu$
), which is the heat transfer non-dimensionalized using the purely conductive heat transfer:
where
![]() $\langle \cdot \rangle _{A}$
indicates the average over any horizontal plane. The simulations were run between 50 and 100 large-eddy turnover times based on
$\langle \cdot \rangle _{A}$
indicates the average over any horizontal plane. The simulations were run between 50 and 100 large-eddy turnover times based on
![]() $U_{f}$
and
$U_{f}$
and
![]() $H$
. Statistical convergence of time averages is assessed by calculating the differences in
$H$
. Statistical convergence of time averages is assessed by calculating the differences in
![]() $Nu$
between one half of the time signal and the full signal. These are shown as error bars in the plots.
$Nu$
between one half of the time signal and the full signal. These are shown as error bars in the plots.
In the classical RB case, both the top and bottom plates have a homogeneous boundary condition, i.e. they are perfectly conducting. Here, we use this boundary condition only for the bottom plate, while the top plate is taken to have periodic patches of insulating regions that do not contribute to the heat transfer from fluid to plate. The definitions of these patches are similar to those in Ripesi et al. (Reference Ripesi, Bigerale, Sbragaglia and Wirth2014):
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\unicode[STIX]{x1D703}(\hat{x},{\hat{y}},\hat{\boldsymbol{z}}=1)=0,\quad \forall ~\hat{x},{\hat{y}}\in [jL_{p},L_{p1}+jL_{p}],~j\in \mathbb{Z},\\ \unicode[STIX]{x2202}_{z}\unicode[STIX]{x1D703}(\hat{x},{\hat{y}},\hat{\boldsymbol{z}}=1)=0,\quad \forall ~x,y\notin [jL_{p},L_{p2}+jL_{p}],~j\in \mathbb{Z},\\ \unicode[STIX]{x1D703}(\hat{x},{\hat{y}},\hat{\boldsymbol{z}}=0)=1,\quad \forall ~x,y.\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\unicode[STIX]{x1D703}(\hat{x},{\hat{y}},\hat{\boldsymbol{z}}=1)=0,\quad \forall ~\hat{x},{\hat{y}}\in [jL_{p},L_{p1}+jL_{p}],~j\in \mathbb{Z},\\ \unicode[STIX]{x2202}_{z}\unicode[STIX]{x1D703}(\hat{x},{\hat{y}},\hat{\boldsymbol{z}}=1)=0,\quad \forall ~x,y\notin [jL_{p},L_{p2}+jL_{p}],~j\in \mathbb{Z},\\ \unicode[STIX]{x1D703}(\hat{x},{\hat{y}},\hat{\boldsymbol{z}}=0)=1,\quad \forall ~x,y.\end{array}\right\}\end{eqnarray}$$
Here
![]() $L_{p}$
is the width of a pair of patches,
$L_{p}$
is the width of a pair of patches,
![]() $L_{p1}$
is the width of the conducting part,
$L_{p1}$
is the width of the conducting part,
![]() $L_{p2}$
is the insulating part, and the hat on the spatial coordinates indicates non-dimensionalizations. For most of this study we keep the insulating and conducting areas equal, i.e.
$L_{p2}$
is the insulating part, and the hat on the spatial coordinates indicates non-dimensionalizations. For most of this study we keep the insulating and conducting areas equal, i.e.
![]() $\ell _{C}=1/2$
. The BC on the top plate depends only on the
$\ell _{C}=1/2$
. The BC on the top plate depends only on the
![]() $x$
-coordinate, which results in sets of insulating and conducting stripes. The number of stripe pairs in a horizontal direction
$x$
-coordinate, which results in sets of insulating and conducting stripes. The number of stripe pairs in a horizontal direction
![]() $L$
were defined as
$L$
were defined as
![]() $f=L/L_{p}$
, which is a central control parameter of this study. A 2D schematic is shown in figure 1.
$f=L/L_{p}$
, which is a central control parameter of this study. A 2D schematic is shown in figure 1.
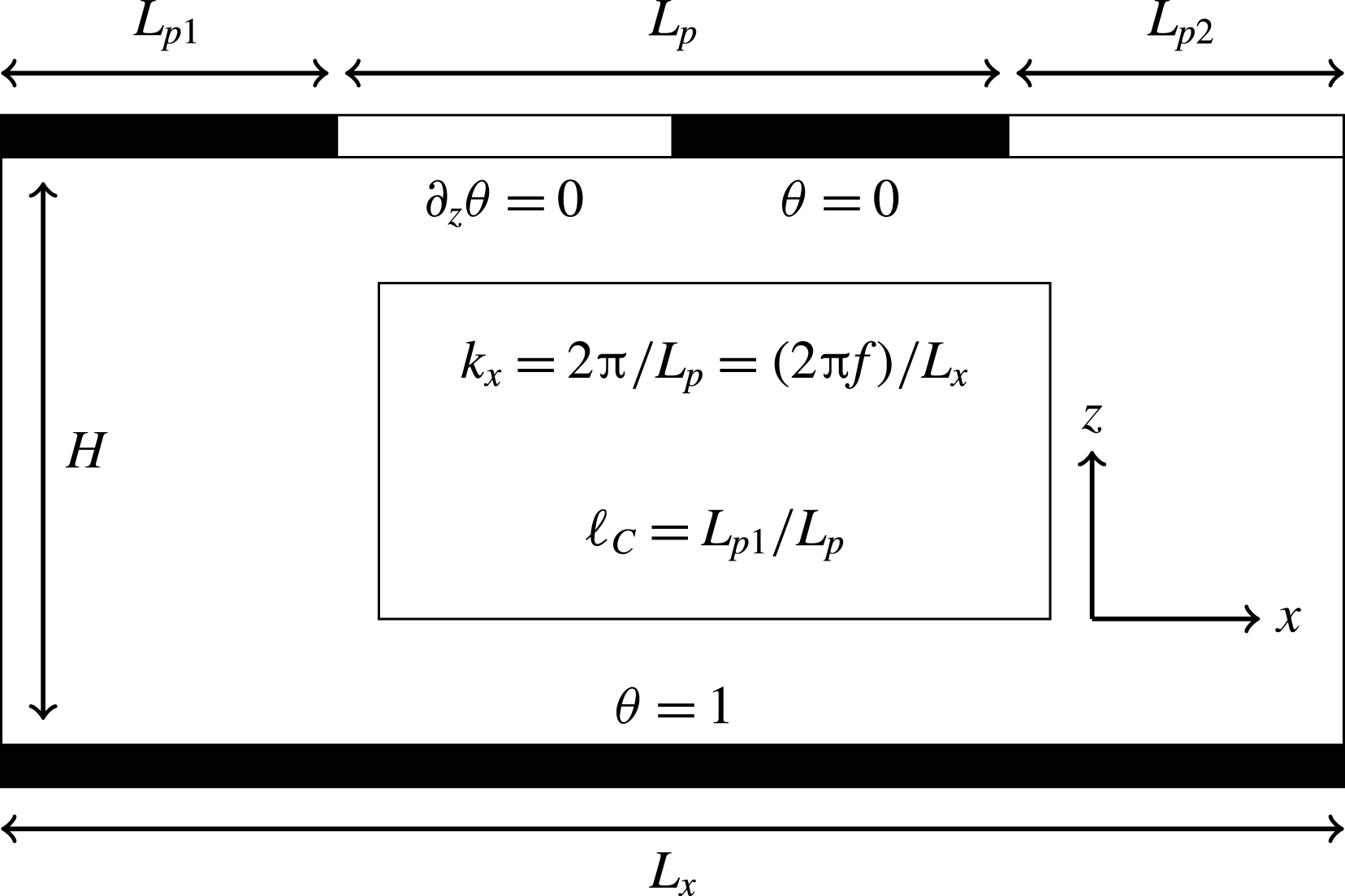
Figure 1. The 2D
![]() $y$
-cut of the geometry. The domain has dimensions
$y$
-cut of the geometry. The domain has dimensions
![]() $L_{x}\times L_{y}\times H$
. The bottom plate, at
$L_{x}\times L_{y}\times H$
. The bottom plate, at
![]() $\hat{\boldsymbol{z}}=0$
, has
$\hat{\boldsymbol{z}}=0$
, has
![]() $\unicode[STIX]{x1D703}=1$
. The top plate is divided into stripes of conducting (
$\unicode[STIX]{x1D703}=1$
. The top plate is divided into stripes of conducting (
![]() $\unicode[STIX]{x1D703}=0$
) and insulating (
$\unicode[STIX]{x1D703}=0$
) and insulating (
![]() $\unicode[STIX]{x2202}_{z}\unicode[STIX]{x1D703}=0$
) regions.
$\unicode[STIX]{x2202}_{z}\unicode[STIX]{x1D703}=0$
) regions.
There are limitations on the value of
![]() $f$
. As each stripe has to be an integer number of grid points, only integer multiples of the grid resolution are valid. In addition, the width of all stripes summed should fit inside the system, e.g. the width in grid points should exactly be the number of grid points in the
$f$
. As each stripe has to be an integer number of grid points, only integer multiples of the grid resolution are valid. In addition, the width of all stripes summed should fit inside the system, e.g. the width in grid points should exactly be the number of grid points in the
![]() $x$
-direction. This results in a total of 18 different pattern frequencies. For the smallest possible frequency,
$x$
-direction. This results in a total of 18 different pattern frequencies. For the smallest possible frequency,
![]() $f=1$
, we have one conducting and one insulating stripe, which both have a width of 180 grid points. The pattern with the largest frequency,
$f=1$
, we have one conducting and one insulating stripe, which both have a width of 180 grid points. The pattern with the largest frequency,
![]() $f=90$
, has 90 stripe pairs, where each stripe has a width of two grid points. In this paper we will use the wavenumber,
$f=90$
, has 90 stripe pairs, where each stripe has a width of two grid points. In this paper we will use the wavenumber,
![]() $k_{x}=(2\unicode[STIX]{x03C0}f)/L_{x}$
, to describe the stripe distribution.
$k_{x}=(2\unicode[STIX]{x03C0}f)/L_{x}$
, to describe the stripe distribution.
To give an idea of how the flow in such a system looks, two different instantaneous snapshots of the RB system with two different stripe frequencies are shown in figure 2. Both cases have exactly the same conducting and insulating areas, but a different stripe pattern. In § 3.4, we also vary the BC in the
![]() $y$
-direction, while keeping both the insulating and conducting areas equal, which results in a chequerboard pattern.
$y$
-direction, while keeping both the insulating and conducting areas equal, which results in a chequerboard pattern.

Figure 2. Two 3D visualizations of the instantaneous temperature field with different pattern frequencies applied to the top boundary. For both cases
![]() $\ell _{C}=0.5$
,
$\ell _{C}=0.5$
,
![]() $Ra=10^{8}$
and
$Ra=10^{8}$
and
![]() $\mathit{Pr}=1$
. Hot fluid is shown in red while cold fluid has a blue colour. (a) Visualization with
$\mathit{Pr}=1$
. Hot fluid is shown in red while cold fluid has a blue colour. (a) Visualization with
![]() $f=4$
, showing four insulating stripes and four conducting stripes. (b) Visualization with
$f=4$
, showing four insulating stripes and four conducting stripes. (b) Visualization with
![]() $f=20$
, showing five times as many stripe pairs. Plumes of colder fluid are ejected primarily from the conducting areas for
$f=20$
, showing five times as many stripe pairs. Plumes of colder fluid are ejected primarily from the conducting areas for
![]() $f=4$
while for
$f=4$
while for
![]() $f=20$
the plumes also eject on areas below insulating regions.
$f=20$
the plumes also eject on areas below insulating regions.
3 Results
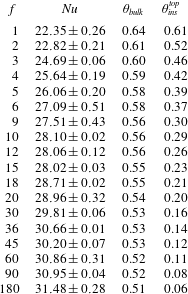
Data from the numerical simulations carried out in this paper are contained in tables 1–4 in appendix A.
3.1 The effect of the number of stripes
In this subsection we present results of a series of simulations in which we varied the number of stripes while keeping
![]() $\ell _{C}=1/2$
. Four sets of cases were run for
$\ell _{C}=1/2$
. Four sets of cases were run for
![]() $Ra=10^{7}$
,
$Ra=10^{7}$
,
![]() $10^{8}$
and
$10^{8}$
and
![]() $10^{9}$
, and
$10^{9}$
, and
![]() $\mathit{Pr}=1$
and
$\mathit{Pr}=1$
and
![]() $10$
.
$10$
.

Figure 3. (a) Nusselt number
![]() $Nu$
and (b) compensated Nusselt number
$Nu$
and (b) compensated Nusselt number
![]() $NuRa^{-0.3}$
against
$NuRa^{-0.3}$
against
![]() $Ra$
for various
$Ra$
for various
![]() $f$
and
$f$
and
![]() $Pr=1$
. The markers show the actual results while the dotted lines indicate the trend between these simulations. For all simulations
$Pr=1$
. The markers show the actual results while the dotted lines indicate the trend between these simulations. For all simulations
![]() $\ell _{C}$
was fixed to
$\ell _{C}$
was fixed to
![]() $\ell _{C}=0.5$
.
$\ell _{C}=0.5$
.
First we show in figure 3(a) the curves of
![]() $Nu$
(
$Nu$
(
![]() $Ra$
) for the fully conducting case and three striped cases with
$Ra$
) for the fully conducting case and three striped cases with
![]() $f=$
1, 10 and 90. The markers show the actual results from the simulations and the dotted lines indicate the trend between the measurements. From figure 3(a) we see that the scaling does not differ significantly between all cases and all curves are almost parallel. We do see a strong dependence on the wavenumber of the pattern. For
$f=$
1, 10 and 90. The markers show the actual results from the simulations and the dotted lines indicate the trend between the measurements. From figure 3(a) we see that the scaling does not differ significantly between all cases and all curves are almost parallel. We do see a strong dependence on the wavenumber of the pattern. For
![]() $f=1$
, we computed that
$f=1$
, we computed that
![]() $Nu$
is approximately two-thirds of the fully conducting case. Increasing
$Nu$
is approximately two-thirds of the fully conducting case. Increasing
![]() $f$
results in a larger
$f$
results in a larger
![]() $Nu$
and the values almost converge with the fully conducting case. Both the
$Nu$
and the values almost converge with the fully conducting case. Both the
![]() $f=90$
and
$f=90$
and
![]() $f=10$
cases are relatively closer to the fully conducting case at
$f=10$
cases are relatively closer to the fully conducting case at
![]() $Ra=10^{7}$
than at
$Ra=10^{7}$
than at
![]() $Ra=3\times 10^{9}$
. Our interpretation is that, due to the lower
$Ra=3\times 10^{9}$
. Our interpretation is that, due to the lower
![]() $Ra$
, the thermal boundary layer is thicker, which results in larger horizontal conduction of heat. As all curves have approximately the same scaling, we have compensated the data using
$Ra$
, the thermal boundary layer is thicker, which results in larger horizontal conduction of heat. As all curves have approximately the same scaling, we have compensated the data using
![]() $Ra^{-0.3}$
, which is shown in figure 3(b). Here it is clearly visible that, for low
$Ra^{-0.3}$
, which is shown in figure 3(b). Here it is clearly visible that, for low
![]() $Ra$
, the
$Ra$
, the
![]() $f=90$
case is almost as efficient as the fully conducting case, but the differences increase with increasing
$f=90$
case is almost as efficient as the fully conducting case, but the differences increase with increasing
![]() $Ra$
. The two extreme cases,
$Ra$
. The two extreme cases,
![]() $f=1$
and the fully conducting case, follow a similar trend; however, the
$f=1$
and the fully conducting case, follow a similar trend; however, the
![]() $f=1$
case is shifted to a lower, less efficient level. Both panels of figure 3 clearly show that an increase in wavenumber of the pattern results in an increase in
$f=1$
case is shifted to a lower, less efficient level. Both panels of figure 3 clearly show that an increase in wavenumber of the pattern results in an increase in
![]() $Nu$
.
$Nu$
.

Figure 4. (a) Nusselt number
![]() $Nu$
for various
$Nu$
for various
![]() $Ra$
and
$Ra$
and
![]() $\mathit{Pr}$
versus pattern wavenumber
$\mathit{Pr}$
versus pattern wavenumber
![]() $k_{x}$
. The shaded area shows the data points for which the stripe width is smaller than the thermal boundary layer. (b) The same data as in panel (a) but normalized by
$k_{x}$
. The shaded area shows the data points for which the stripe width is smaller than the thermal boundary layer. (b) The same data as in panel (a) but normalized by
![]() $Nu_{fc}$
. The black points are the same as in the shaded area in panel (a). For both panels, the error bars shows the statistical convergence error.
$Nu_{fc}$
. The black points are the same as in the shaded area in panel (a). For both panels, the error bars shows the statistical convergence error.
To make this point even more clear, we plotted
![]() $Nu$
(
$Nu$
(
![]() $k_{x}$
) in figure 4(a). All datasets show a clear
$k_{x}$
) in figure 4(a). All datasets show a clear
![]() $k_{x}$
dependence:
$k_{x}$
dependence:
![]() $Nu$
increases quite strongly with
$Nu$
increases quite strongly with
![]() $k_{x}$
. The grey area indicates the data points for which the width of the stripes
$k_{x}$
. The grey area indicates the data points for which the width of the stripes
![]() $L_{p}$
is smaller than the thermal boundary layer thickness
$L_{p}$
is smaller than the thermal boundary layer thickness
![]() $\unicode[STIX]{x1D706}_{T}$
, which can be estimated as
$\unicode[STIX]{x1D706}_{T}$
, which can be estimated as
![]() $\unicode[STIX]{x1D706}_{T}=H/(2Nu)$
. Ripesi et al. (Reference Ripesi, Bigerale, Sbragaglia and Wirth2014) showed that the heat transfer increases monotonically with increasing
$\unicode[STIX]{x1D706}_{T}=H/(2Nu)$
. Ripesi et al. (Reference Ripesi, Bigerale, Sbragaglia and Wirth2014) showed that the heat transfer increases monotonically with increasing
![]() $k_{x}$
until
$k_{x}$
until
![]() $L_{p}$
is comparable to
$L_{p}$
is comparable to
![]() $\unicode[STIX]{x1D706}_{T}$
. A similar trend is visible for
$\unicode[STIX]{x1D706}_{T}$
. A similar trend is visible for
![]() $Ra=1\times 10^{7}$
and
$Ra=1\times 10^{7}$
and
![]() $Ra=1\times 10^{8}$
even if the
$Ra=1\times 10^{8}$
even if the
![]() $Ra=1\times 10^{7}$
case shows minor increases in heat transfer when
$Ra=1\times 10^{7}$
case shows minor increases in heat transfer when
![]() $L_{p}$
is further decreased beyond
$L_{p}$
is further decreased beyond
![]() $\unicode[STIX]{x1D706}_{T}$
. The change in
$\unicode[STIX]{x1D706}_{T}$
. The change in
![]() $\mathit{Pr}$
from
$\mathit{Pr}$
from
![]() $\mathit{Pr}=1$
to
$\mathit{Pr}=1$
to
![]() $\mathit{Pr}=10$
does not have a significant effect on the heat transfer, at least not for
$\mathit{Pr}=10$
does not have a significant effect on the heat transfer, at least not for
![]() $Ra=10^{8}$
, for which the two datasets are practically overlapping. This behaviour is similar to the standard RB case, in which the
$Ra=10^{8}$
, for which the two datasets are practically overlapping. This behaviour is similar to the standard RB case, in which the
![]() $\mathit{Pr}$
dependence of
$\mathit{Pr}$
dependence of
![]() $Nu$
is also weak (Ahlers et al.
Reference Ahlers, Grossmann and Lohse2009).
$Nu$
is also weak (Ahlers et al.
Reference Ahlers, Grossmann and Lohse2009).
To perform a better comparison between the different
![]() $Ra$
, we normalize the resulting
$Ra$
, we normalize the resulting
![]() $Nu$
using
$Nu$
using
![]() $Nu_{fc}$
, the Nusselt number of the fully conducting case. The normalized
$Nu_{fc}$
, the Nusselt number of the fully conducting case. The normalized
![]() $Nu$
for different stripe configurations are shown in figure 4(b). We see the same trend for all
$Nu$
for different stripe configurations are shown in figure 4(b). We see the same trend for all
![]() $Ra$
and
$Ra$
and
![]() $\mathit{Pr}$
. At the lowest
$\mathit{Pr}$
. At the lowest
![]() $k_{x}$
, in which we only have a single conducting and single insulating stripe, the effective
$k_{x}$
, in which we only have a single conducting and single insulating stripe, the effective
![]() $Nu$
is approximately two-thirds of the fully conducting case. When the number of stripes, i.e.
$Nu$
is approximately two-thirds of the fully conducting case. When the number of stripes, i.e.
![]() $k_{x}$
, is increased, we see that, for all tested
$k_{x}$
, is increased, we see that, for all tested
![]() $Ra$
and
$Ra$
and
![]() $\mathit{Pr}$
, the Nusselt number slowly converges to almost the fully conducting case. So, remarkably, even if only half of the plate is conducting, it can be almost as effective as if the plate is fully conducting. In this compensated plot it is also clearly visible that, for the largest
$\mathit{Pr}$
, the Nusselt number slowly converges to almost the fully conducting case. So, remarkably, even if only half of the plate is conducting, it can be almost as effective as if the plate is fully conducting. In this compensated plot it is also clearly visible that, for the largest
![]() $k_{x}$
of
$k_{x}$
of
![]() $Ra=1\times 10^{7}$
, for which
$Ra=1\times 10^{7}$
, for which
![]() $L_{p}$
goes below the size of
$L_{p}$
goes below the size of
![]() $\unicode[STIX]{x1D706}_{T}$
, the heat transfer is still increasing.
$\unicode[STIX]{x1D706}_{T}$
, the heat transfer is still increasing.
The differences between the different
![]() $Ra$
are not so clear at the lowest
$Ra$
are not so clear at the lowest
![]() $k_{x}$
; however, for a slight increase of
$k_{x}$
; however, for a slight increase of
![]() $k_{x}$
we see that the curves order themselves. The
$k_{x}$
we see that the curves order themselves. The
![]() $Ra=10^{9}$
case increases slightly slower with
$Ra=10^{9}$
case increases slightly slower with
![]() $k_{s}$
when compared to the
$k_{s}$
when compared to the
![]() $Ra=10^{8}$
case. The
$Ra=10^{8}$
case. The
![]() $Ra=10^{7}$
case increases slightly faster than the
$Ra=10^{7}$
case increases slightly faster than the
![]() $Ra=10^{8}$
case and it ends at 99.7 % of the fully conducting case for the largest number of stripes used. The explanation for this trend is the difference in boundary layer thickness, which decreases when we increase
$Ra=10^{8}$
case and it ends at 99.7 % of the fully conducting case for the largest number of stripes used. The explanation for this trend is the difference in boundary layer thickness, which decreases when we increase
![]() $Ra$
. The boundary layer controls the heat transport from the bulk to the conducting region. Below the insulating region, this heat transport must also go in the horizontal direction. By increasing
$Ra$
. The boundary layer controls the heat transport from the bulk to the conducting region. Below the insulating region, this heat transport must also go in the horizontal direction. By increasing
![]() $Ra$
and thus decreasing the thickness of the boundary layer, the same amount of heat needs to be conducted through a smaller ‘channel’. This explains the decreased effectiveness with increasing
$Ra$
and thus decreasing the thickness of the boundary layer, the same amount of heat needs to be conducted through a smaller ‘channel’. This explains the decreased effectiveness with increasing
![]() $Ra$
.
$Ra$
.
In these sets of simulations, we also compare
![]() $\mathit{Pr}=10$
with
$\mathit{Pr}=10$
with
![]() $\mathit{Pr}=1$
for
$\mathit{Pr}=1$
for
![]() $Ra=10^{8}$
. The results for both
$Ra=10^{8}$
. The results for both
![]() $\mathit{Pr}$
are quite similar. At lower
$\mathit{Pr}$
are quite similar. At lower
![]() $k_{x}$
, we see that the
$k_{x}$
, we see that the
![]() $\mathit{Pr}=10$
case has only a marginally larger
$\mathit{Pr}=10$
case has only a marginally larger
![]() $Nu$
and these differences become smaller with increasing
$Nu$
and these differences become smaller with increasing
![]() $k_{x}$
and are within the uncertainty of the simulation.
$k_{x}$
and are within the uncertainty of the simulation.
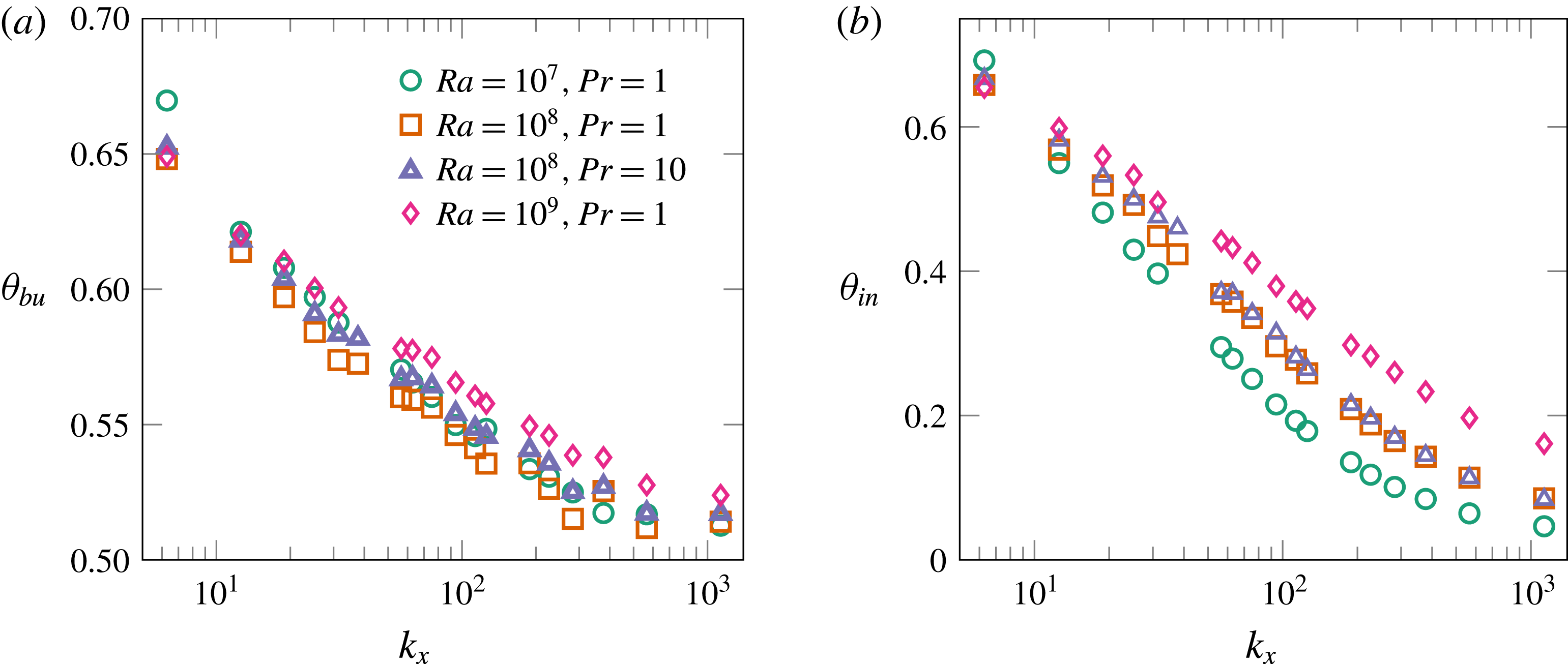
Figure 5. (a) Temperature of the bulk fluid
![]() $\unicode[STIX]{x1D703}_{bu}$
for various Ra and
$\unicode[STIX]{x1D703}_{bu}$
for various Ra and
![]() $\mathit{Pr}$
versus pattern wavenumber
$\mathit{Pr}$
versus pattern wavenumber
![]() $k_{x}$
. (b) Temperature below the insulating stripes
$k_{x}$
. (b) Temperature below the insulating stripes
![]() $\unicode[STIX]{x1D703}_{in}$
, averaged over the entire insulating area, for different
$\unicode[STIX]{x1D703}_{in}$
, averaged over the entire insulating area, for different
![]() $Ra$
and
$Ra$
and
![]() $\mathit{Pr}$
against pattern wavenumber
$\mathit{Pr}$
against pattern wavenumber
![]() $k_{x}$
.
$k_{x}$
.
Figure 5(a) shows the average bulk temperature of the fluid plotted against the wavenumber. This average was computed over the horizontal plane at mid-height of the system. The effect is similar to what we see for
![]() $Nu/Nu_{fc}$
in figure 4(b). At the lowest
$Nu/Nu_{fc}$
in figure 4(b). At the lowest
![]() $k_{x}$
the average bulk temperature has increased to about
$k_{x}$
the average bulk temperature has increased to about
![]() $2/3$
. In that case the top plate is split in half and only one half is contributing to heat transfer. While ignoring the adiabatic area, we can divide the conducting areas into three equally sized parts, with two parts on the bottom plate and one on the top plate. Using the same reasoning as that used for the symmetric case, we obtain the following equality for the average bulk temperature:
$2/3$
. In that case the top plate is split in half and only one half is contributing to heat transfer. While ignoring the adiabatic area, we can divide the conducting areas into three equally sized parts, with two parts on the bottom plate and one on the top plate. Using the same reasoning as that used for the symmetric case, we obtain the following equality for the average bulk temperature:
![]() $\unicode[STIX]{x1D703}_{bulk}=(2/3)\unicode[STIX]{x1D703}_{bottom}+(1/3)\unicode[STIX]{x1D703}_{top}=2/3$
. As with
$\unicode[STIX]{x1D703}_{bulk}=(2/3)\unicode[STIX]{x1D703}_{bottom}+(1/3)\unicode[STIX]{x1D703}_{top}=2/3$
. As with
![]() $Nu/Nu_{fc}$
, we see that the average bulk temperature approaches the fully conducting case of
$Nu/Nu_{fc}$
, we see that the average bulk temperature approaches the fully conducting case of
![]() $\unicode[STIX]{x1D703}_{bulk}=1/2$
for increasing
$\unicode[STIX]{x1D703}_{bulk}=1/2$
for increasing
![]() $k_{x}$
. When comparing the various curves, they all appear similar, with a maximum difference of about 0.02–0.03 in the average bulk temperature. Unfortunately, Wang et al. (Reference Wang, Huang and Xia2017) do not report their average temperature and a comparison to their calculations with large-wavelength imperfect BCs is impossible.
$k_{x}$
. When comparing the various curves, they all appear similar, with a maximum difference of about 0.02–0.03 in the average bulk temperature. Unfortunately, Wang et al. (Reference Wang, Huang and Xia2017) do not report their average temperature and a comparison to their calculations with large-wavelength imperfect BCs is impossible.
In figure 5(b) we show the horizontally and time-averaged temperature below the insulating area of the top plate as a function of the wavenumber. At the lowest wavenumber (top plate split into equal conducting and insulating regions), we see that the averaged temperature is almost equal for all
![]() $Ra$
and
$Ra$
and
![]() $\mathit{Pr}$
. When increasing
$\mathit{Pr}$
. When increasing
![]() $k_{x}$
, a dependence on
$k_{x}$
, a dependence on
![]() $Ra$
emerges. After just a few additional divisions in stripes, all curves order themselves according to
$Ra$
emerges. After just a few additional divisions in stripes, all curves order themselves according to
![]() $Ra$
, with the lower
$Ra$
, with the lower
![]() $Ra$
values approaching the lower bounds faster than the larger ones. At the largest
$Ra$
values approaching the lower bounds faster than the larger ones. At the largest
![]() $k_{x}$
, the temperature difference between
$k_{x}$
, the temperature difference between
![]() $Ra=10^{9}$
and
$Ra=10^{9}$
and
![]() $Ra=10^{7}$
is 15 %. As the temperature below the insulating area is slightly higher than for the area below the conducting area because of lack of cooling, we can conclude that, for larger
$Ra=10^{7}$
is 15 %. As the temperature below the insulating area is slightly higher than for the area below the conducting area because of lack of cooling, we can conclude that, for larger
![]() $Ra$
, the whole top layer is, on average, hotter than for the lower
$Ra$
, the whole top layer is, on average, hotter than for the lower
![]() $Ra$
.
$Ra$
.
These results suggest that it could be possible to account for the
![]() $Nu(k_{x})$
relationship by using corrected non-dimensional variables in the spirit of Verzicco (Reference Verzicco2004). However, changing the (effective) thermal conductivity ignores the heterogeneities of the plate, which is the main source of the observed behaviour. In figure 6, we show the corrected Nusselt number
$Nu(k_{x})$
relationship by using corrected non-dimensional variables in the spirit of Verzicco (Reference Verzicco2004). However, changing the (effective) thermal conductivity ignores the heterogeneities of the plate, which is the main source of the observed behaviour. In figure 6, we show the corrected Nusselt number
![]() $Nu^{\ast }=Nu/\unicode[STIX]{x1D703}^{\ast }$
against the corrected Rayleigh number
$Nu^{\ast }=Nu/\unicode[STIX]{x1D703}^{\ast }$
against the corrected Rayleigh number
![]() $Ra^{\ast }=Ra\unicode[STIX]{x1D703}^{\ast }$
, where
$Ra^{\ast }=Ra\unicode[STIX]{x1D703}^{\ast }$
, where
![]() $\unicode[STIX]{x1D703}^{\ast }$
is the non-dimensional average temperature difference given by
$\unicode[STIX]{x1D703}^{\ast }$
is the non-dimensional average temperature difference given by
![]() $\unicode[STIX]{x1D703}^{\ast }=L_{p2}\unicode[STIX]{x1D703}_{in}/L_{p}$
. No logical ordering can be seen, and, as expected, an attempt to describe the results with some global effective thermal conductivity fails.
$\unicode[STIX]{x1D703}^{\ast }=L_{p2}\unicode[STIX]{x1D703}_{in}/L_{p}$
. No logical ordering can be seen, and, as expected, an attempt to describe the results with some global effective thermal conductivity fails.
Figure 6. (a) Corrected Nusselt number against compensated Rayleigh number for selected pattern wavelengths. (b) Compensated and corrected Nusselt number against corrected Rayleigh number. No collapse or natural ordering of the curves can be seen.
For horizontal slices of the instantaneous temperature field, a discrete 2D Fourier transform can be applied, which is defined as
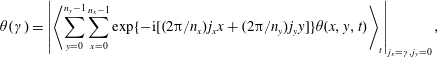 $$\begin{eqnarray}\unicode[STIX]{x1D703}(\unicode[STIX]{x1D6FE})=\mathop{\left|\mathop{\left\langle \mathop{\sum }_{y=0}^{n_{y}-1}\mathop{\sum }_{x=0}^{n_{x}-1}\exp \{-\text{i}[(2\unicode[STIX]{x03C0}/n_{x})j_{x}x+(2\unicode[STIX]{x03C0}/n_{y})j_{y}y]\}\unicode[STIX]{x1D703}(x,y,t)\right\rangle }\nolimits_{t}\right|}\nolimits_{j_{x}=\unicode[STIX]{x1D6FE},j_{y}=0},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D703}(\unicode[STIX]{x1D6FE})=\mathop{\left|\mathop{\left\langle \mathop{\sum }_{y=0}^{n_{y}-1}\mathop{\sum }_{x=0}^{n_{x}-1}\exp \{-\text{i}[(2\unicode[STIX]{x03C0}/n_{x})j_{x}x+(2\unicode[STIX]{x03C0}/n_{y})j_{y}y]\}\unicode[STIX]{x1D703}(x,y,t)\right\rangle }\nolimits_{t}\right|}\nolimits_{j_{x}=\unicode[STIX]{x1D6FE},j_{y}=0},\end{eqnarray}$$
where
![]() $\langle \cdot \rangle _{t}$
is the time average and the
$\langle \cdot \rangle _{t}$
is the time average and the
![]() $j_{y}$
mode was set to zero, leaving a single wavenumber parameter
$j_{y}$
mode was set to zero, leaving a single wavenumber parameter
![]() $\unicode[STIX]{x1D6FE}\equiv j_{x}$
. Using the described method on the horizontal slice just below the top boundary, we can identify the imprint the stripe-structured BCs leaves on the flow.
$\unicode[STIX]{x1D6FE}\equiv j_{x}$
. Using the described method on the horizontal slice just below the top boundary, we can identify the imprint the stripe-structured BCs leaves on the flow.
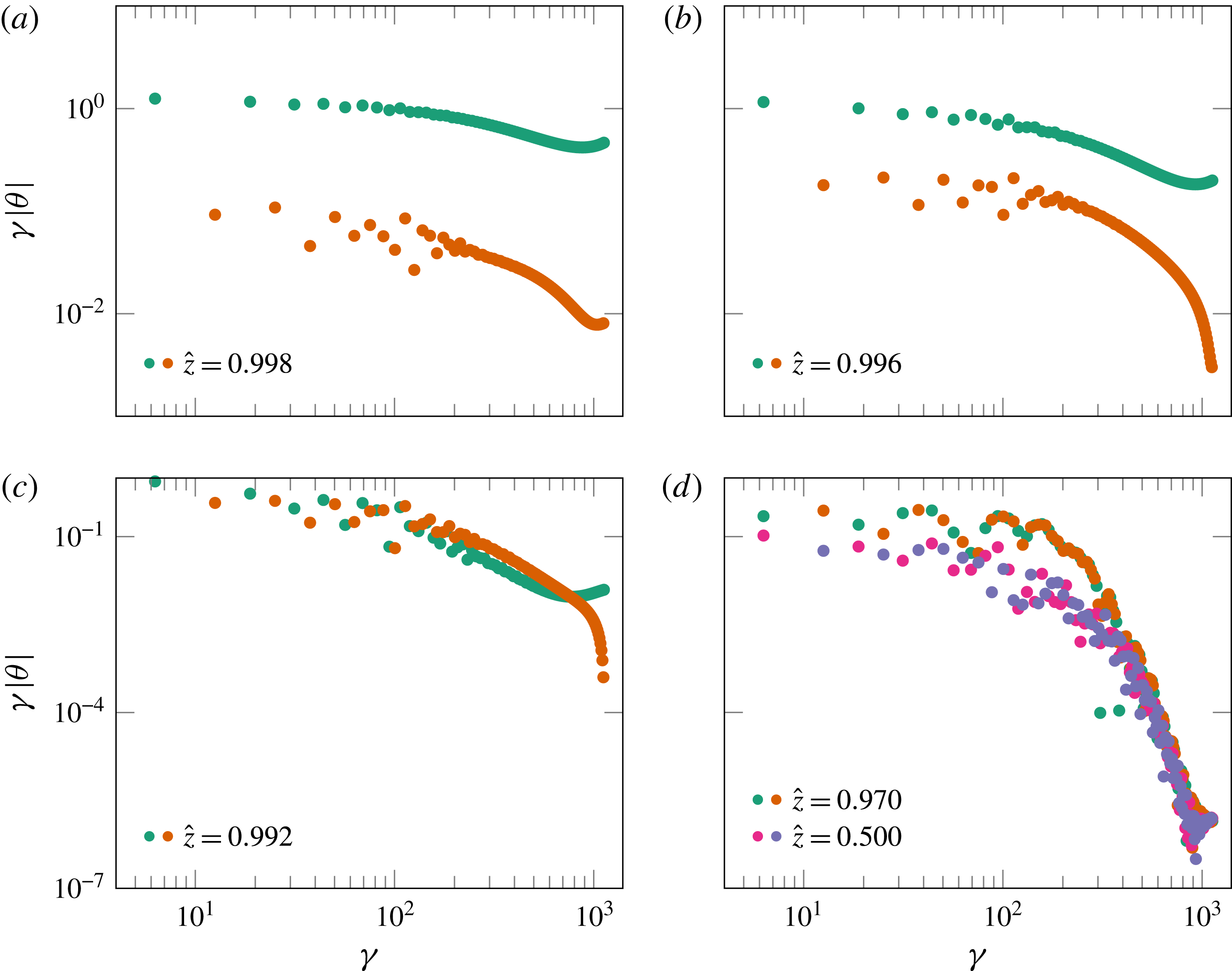
Figure 7. Premultiplied 2D Fourier transform of a horizontal slice at various distances from the top boundary wall, averaged in time. Except for (d), each panel is compiled using a single dataset. The colours help to identify the different modes that are present in each single dataset and are identified by the odd or even value. (a) At the closest grid point (
![]() $\hat{\boldsymbol{z}}=0.998$
), the two different modes are clearly visible. (b) One grid point further (
$\hat{\boldsymbol{z}}=0.998$
), the two different modes are clearly visible. (b) One grid point further (
![]() $\hat{\boldsymbol{z}}=0.996$
), the distinction slowly fades. (c) While still inside the boundary layer at
$\hat{\boldsymbol{z}}=0.996$
), the distinction slowly fades. (c) While still inside the boundary layer at
![]() $\hat{\boldsymbol{z}}=0.992$
, both modes are practically overlapping. (d) Just outside the boundary layer, it is impossible to distinguish two different modes at all. As a reference, we also show the spectrum at the centre of the system (
$\hat{\boldsymbol{z}}=0.992$
, both modes are practically overlapping. (d) Just outside the boundary layer, it is impossible to distinguish two different modes at all. As a reference, we also show the spectrum at the centre of the system (
![]() $\hat{\boldsymbol{z}}=0.5$
).
$\hat{\boldsymbol{z}}=0.5$
).
Using the Fourier transform we can identify the imprint of the BCs just below the top boundary in the flow itself. Using this distinct signature we can find out how long this pattern is still present once one moves away from the boundary wall. The distance from the top boundary wall is indicated using
![]() $\hat{\boldsymbol{z}}$
. In figure 7, we see the compensated spectra for
$\hat{\boldsymbol{z}}$
. In figure 7, we see the compensated spectra for
![]() $f=1$
at five different planes for decreasing
$f=1$
at five different planes for decreasing
![]() $\hat{\boldsymbol{z}}$
. The colours are used to identify the different modes and except for figure 7(d) are compiled using a single dataset (odd or even value). When moving away from the wall, we see that the two distinct modes approach each other and just outside the boundary layer, at
$\hat{\boldsymbol{z}}$
. The colours are used to identify the different modes and except for figure 7(d) are compiled using a single dataset (odd or even value). When moving away from the wall, we see that the two distinct modes approach each other and just outside the boundary layer, at
![]() $\hat{\boldsymbol{z}}=0.970$
, it is hard to distinguish the two different curves at all. Within the boundary layer the signature of the pattern almost completely fades away and in the bulk flow is not visible at all. The difference between the Fourier transform just outside the boundary layer (
$\hat{\boldsymbol{z}}=0.970$
, it is hard to distinguish the two different curves at all. Within the boundary layer the signature of the pattern almost completely fades away and in the bulk flow is not visible at all. The difference between the Fourier transform just outside the boundary layer (
![]() $\hat{\boldsymbol{z}}=0.970$
) and at mid-height of the system (
$\hat{\boldsymbol{z}}=0.970$
) and at mid-height of the system (
![]() $\hat{\boldsymbol{z}}=0.5$
) is marginal. These findings hold for the complete range of
$\hat{\boldsymbol{z}}=0.5$
) is marginal. These findings hold for the complete range of
![]() $f$
.
$f$
.
It is quite remarkable that, even for the most extreme case at
![]() $f=1$
, the pattern is not visible in the bulk region. This means that in the boundary layer, in which conduction dominates, the temperature differences of the top plate are averaged such that an effective, slightly higher cold plate is seen by the bulk flow.
$f=1$
, the pattern is not visible in the bulk region. This means that in the boundary layer, in which conduction dominates, the temperature differences of the top plate are averaged such that an effective, slightly higher cold plate is seen by the bulk flow.
Figure 8. (a) Comparison of the normalized Nusselt number
![]() $Nu/Nu_{fc}$
for the single- and double-sided cases with
$Nu/Nu_{fc}$
for the single- and double-sided cases with
![]() $Ra=10^{8}$
,
$Ra=10^{8}$
,
![]() $\mathit{Pr}=1$
and
$\mathit{Pr}=1$
and
![]() $\ell _{C}=0.5$
. For the lowest
$\ell _{C}=0.5$
. For the lowest
![]() $k_{s}$
we see that the system is about two-thirds and one-half of the fully conducting case for the single- and double-sided cases, respectively. (b) Average temperature above or below the insulating stripes for the single- and double-sided cases with
$k_{s}$
we see that the system is about two-thirds and one-half of the fully conducting case for the single- and double-sided cases, respectively. (b) Average temperature above or below the insulating stripes for the single- and double-sided cases with
![]() $Ra=10^{8}$
,
$Ra=10^{8}$
,
![]() $\mathit{Pr}=1$
and
$\mathit{Pr}=1$
and
![]() $\ell _{C}=0.5$
. The dashed line shows the average bulk temperature, calculated at mid-height for the double-sided system.
$\ell _{C}=0.5$
. The dashed line shows the average bulk temperature, calculated at mid-height for the double-sided system.
3.2 Patterns on both plates
Until now we have only applied the insulating and conducting patches to the top boundary. This resulted in a normalized heat transfer of approximately two-thirds for the lowest
![]() $k_{x}$
and almost the fully conducting case at the highest
$k_{x}$
and almost the fully conducting case at the highest
![]() $k_{x}$
. Using a simple argument we could indeed rationalize the value of two-thirds for the normalized heat transfer for the lowest wavenumber. If we now apply the same pattern also on the bottom plate, can we still get to the same efficiency as if we had only applied the pattern to the top boundary wall?
$k_{x}$
. Using a simple argument we could indeed rationalize the value of two-thirds for the normalized heat transfer for the lowest wavenumber. If we now apply the same pattern also on the bottom plate, can we still get to the same efficiency as if we had only applied the pattern to the top boundary wall?
The comparison of the normalized Nusselt number
![]() $Nu/Nu_{fc}$
between the single- and double-sided cases is shown in figure 8(a). For the lowest
$Nu/Nu_{fc}$
between the single- and double-sided cases is shown in figure 8(a). For the lowest
![]() $k_{x}$
we see that the double-sided case conducts heat at approximately half the rate of the fully conducting case. This is in line with the expectations, as we only have half the effective area on both boundary walls. What is also visible is that the curve for the double-sided case is steeper than the curve of the single-sided case, therefore reducing the difference between both cases with increasing
$k_{x}$
we see that the double-sided case conducts heat at approximately half the rate of the fully conducting case. This is in line with the expectations, as we only have half the effective area on both boundary walls. What is also visible is that the curve for the double-sided case is steeper than the curve of the single-sided case, therefore reducing the difference between both cases with increasing
![]() $k_{x}$
. For the largest
$k_{x}$
. For the largest
![]() $k_{x}$
the heat transfer of this system again is almost as efficient as if it were fully conducting. There is only half of the area available for heat entering the system and only half the area for heat leaving the system. Still, the same amount of heat transfer as if the system were fully conducting is achieved. For the single-sided case, as for the double-sided one, for the lowest
$k_{x}$
the heat transfer of this system again is almost as efficient as if it were fully conducting. There is only half of the area available for heat entering the system and only half the area for heat leaving the system. Still, the same amount of heat transfer as if the system were fully conducting is achieved. For the single-sided case, as for the double-sided one, for the lowest
![]() $k_{x}$
the efficiency is not exactly
$k_{x}$
the efficiency is not exactly
![]() $2/3$
and
$2/3$
and
![]() $1/2$
but slightly above these values. The geometry of the double-sided case can be decomposed into a regular RB cell and a neutral domain, both with identical dimensions, positioned next to each other. The top and bottom boundaries from this neutral domain are both insulating and heat can only enter and exit from the sides. As we have periodic BCs in the horizontal direction, both sides of the regular RB area are connected to this neutral domain, which acts as a buffer for heat. This extra buffer is the only difference and thus the cause for the small difference.
$1/2$
but slightly above these values. The geometry of the double-sided case can be decomposed into a regular RB cell and a neutral domain, both with identical dimensions, positioned next to each other. The top and bottom boundaries from this neutral domain are both insulating and heat can only enter and exit from the sides. As we have periodic BCs in the horizontal direction, both sides of the regular RB area are connected to this neutral domain, which acts as a buffer for heat. This extra buffer is the only difference and thus the cause for the small difference.
The average temperatures just below or above the insulating boundaries are shown against
![]() $k_{x}$
in figure 8(b). The difference in temperature below the top insulating boundary between the single-sided case, shown in green circles, and the double-sided case, shown in orange squares, is only significant at the lowest
$k_{x}$
in figure 8(b). The difference in temperature below the top insulating boundary between the single-sided case, shown in green circles, and the double-sided case, shown in orange squares, is only significant at the lowest
![]() $k_{x}$
. Only at the lower
$k_{x}$
. Only at the lower
![]() $k_{x}$
is the single-sided system hotter, just below the boundary. At larger
$k_{x}$
is the single-sided system hotter, just below the boundary. At larger
![]() $k_{x}$
, the asymmetry does not make a difference to the temperatures and both temperatures converge to the conducting plate temperature. In the same plot, we also show the temperature just above the insulating area of the bottom plate and the bulk temperature. For the double-sided case, for the lowest
$k_{x}$
, the asymmetry does not make a difference to the temperatures and both temperatures converge to the conducting plate temperature. In the same plot, we also show the temperature just above the insulating area of the bottom plate and the bulk temperature. For the double-sided case, for the lowest
![]() $k_{x}$
, the top, bottom and bulk temperatures are very similar. This indicates that for the lowest
$k_{x}$
, the top, bottom and bulk temperatures are very similar. This indicates that for the lowest
![]() $k_{x}$
all the fluid in the neutral domain, the large area confined by the insulating bottom and top plates, has approximately the same temperature and hardly contributes to the heat transfer. This fully agrees with
$k_{x}$
all the fluid in the neutral domain, the large area confined by the insulating bottom and top plates, has approximately the same temperature and hardly contributes to the heat transfer. This fully agrees with
![]() $Nu/Nu_{fc}\approx 0.5$
seen in figure 8(a). The bulk temperature of the double-sided case stays approximately 0.5 for the full range of
$Nu/Nu_{fc}\approx 0.5$
seen in figure 8(a). The bulk temperature of the double-sided case stays approximately 0.5 for the full range of
![]() $k_{x}$
, as must hold for a symmetric system. Temperatures above the bottom boundary and below the top boundary are also symmetric with respect to the bulk temperature, confirming the statistical convergence of our calculations. As for the single-sided case, figure 8(b) shows that for the largest
$k_{x}$
, as must hold for a symmetric system. Temperatures above the bottom boundary and below the top boundary are also symmetric with respect to the bulk temperature, confirming the statistical convergence of our calculations. As for the single-sided case, figure 8(b) shows that for the largest
![]() $k_{x}$
the temperatures close to the insulating areas are very close to their conducting counterparts. The heat conduction in the boundary layer makes the bulk fluid see an almost perfect heat conductor.
$k_{x}$
the temperatures close to the insulating areas are very close to their conducting counterparts. The heat conduction in the boundary layer makes the bulk fluid see an almost perfect heat conductor.
3.3 Variation of the insulating fraction
All the systems that we have discussed until now had a conducting area with size equal to the insulating area, i.e.
![]() $\ell _{C}=1/2$
. We can now vary
$\ell _{C}=1/2$
. We can now vary
![]() $\ell _{C}$
and look into its effect on the heat transfer. In the previous simulations we used
$\ell _{C}$
and look into its effect on the heat transfer. In the previous simulations we used
![]() $k_{x}$
as the wavenumber and this sets the number of insulating and conducting stripes in the 2D case. The width of the system,
$k_{x}$
as the wavenumber and this sets the number of insulating and conducting stripes in the 2D case. The width of the system,
![]() $L_{x}$
, was divided into
$L_{x}$
, was divided into
![]() $f$
equal pairs of these stripes. In the previous subsection, these divisions were of equal areas. Now we will change the ratio of areas to make the top plate less and less conducting. For these simulations we fixed
$f$
equal pairs of these stripes. In the previous subsection, these divisions were of equal areas. Now we will change the ratio of areas to make the top plate less and less conducting. For these simulations we fixed
![]() $k_{x}=9$
,
$k_{x}=9$
,
![]() $Ra=10^{8}$
and
$Ra=10^{8}$
and
![]() $\mathit{Pr}=1$
. Then the ratio between the insulating and conducting areas was varied, namely we simulated
$\mathit{Pr}=1$
. Then the ratio between the insulating and conducting areas was varied, namely we simulated
![]() $\ell _{C}=1.0,~0.875,~0.75,~0.625,~0.50$
and
$\ell _{C}=1.0,~0.875,~0.75,~0.625,~0.50$
and
![]() $0.25$
, thus gradually reducing the conducting area of the top plate from fully conducting to 25 % conducting.
$0.25$
, thus gradually reducing the conducting area of the top plate from fully conducting to 25 % conducting.
Figure 9 shows the results of the simulations, as well as the data from the rectangular tank of the experiments in Wang et al. (Reference Wang, Huang and Xia2017) (extrapolated from their table 1). In the case where only 12.5 % of the area is insulating, we see that the difference with the fully conducting case is almost negligible and within the statistical error. On increasing the amount of insulating area to 25 %, the heat transfer is still more than 90 % of the fully conducting case. Even at 50 % conducting region we still get the effectiveness of 80 %. At the largest ratio of 75 % insulating fraction, we are still above 60 % of the heat transfer of the fully conducting case. In other words, the effective area of the top plate is only a quarter of the fully conducting case but still we get a system that is only 40 % less effective in conducting heat.
The rectangular tank of Wang et al. (Reference Wang, Huang and Xia2017) has patches with dimensions comparable to the system size. Two data points for the two different wavelengths are available for each
![]() $\ell _{C}$
. The data point with a smaller wavelength (‘ACA’ and ‘CAC’ patterns) corresponds to the higher values of
$\ell _{C}$
. The data point with a smaller wavelength (‘ACA’ and ‘CAC’ patterns) corresponds to the higher values of
![]() $Nu$
. While the points at
$Nu$
. While the points at
![]() $\ell _{C}=1/3$
show a considerably lower
$\ell _{C}=1/3$
show a considerably lower
![]() $Nu$
than the DNS with a much smaller wavelength, a relatively good match between DNS and the experiment for
$Nu$
than the DNS with a much smaller wavelength, a relatively good match between DNS and the experiment for
![]() $\ell _{C}=2/3$
provides some indication that at higher values of
$\ell _{C}=2/3$
provides some indication that at higher values of
![]() $\ell _{C}$
the saturation wavenumbers, for which
$\ell _{C}$
the saturation wavenumbers, for which
![]() $Nu\approx Nu_{fc}$
, are smaller.
$Nu\approx Nu_{fc}$
, are smaller.
Figure 9. (a) Normalized Nusselt number
![]() $Nu/Nu_{fc}$
for various fractions
$Nu/Nu_{fc}$
for various fractions
![]() $\ell _{C}$
of the conducting plate, while keeping the pattern frequency
$\ell _{C}$
of the conducting plate, while keeping the pattern frequency
![]() $f=9$
,
$f=9$
,
![]() $Ra=10^{8}$
and
$Ra=10^{8}$
and
![]() $\mathit{Pr}=1$
(green circles), and the rectangular tank of Wang et al. (Reference Wang, Huang and Xia2017) (orange squares). (b) Average temperature just below the insulating area
$\mathit{Pr}=1$
(green circles), and the rectangular tank of Wang et al. (Reference Wang, Huang and Xia2017) (orange squares). (b) Average temperature just below the insulating area
![]() $\unicode[STIX]{x1D703}_{in}$
and average bulk temperature
$\unicode[STIX]{x1D703}_{in}$
and average bulk temperature
![]() $\unicode[STIX]{x1D703}_{bu}$
, both plotted against
$\unicode[STIX]{x1D703}_{bu}$
, both plotted against
![]() $\ell _{C}$
. Other parameters are the same as for panel (a).
$\ell _{C}$
. Other parameters are the same as for panel (a).
Figure 9(b) shows two different temperatures, namely, the average temperature just below the insulating region
![]() $\unicode[STIX]{x1D703}_{in}$
and the average bulk temperature
$\unicode[STIX]{x1D703}_{in}$
and the average bulk temperature
![]() $\unicode[STIX]{x1D703}_{bu}$
measured at mid-height of the system. For
$\unicode[STIX]{x1D703}_{bu}$
measured at mid-height of the system. For
![]() $\ell _{C}=0.85$
,
$\ell _{C}=0.85$
,
![]() $\unicode[STIX]{x1D703}_{in}$
is very close to zero, i.e. the top wall temperature. This is consistent with
$\unicode[STIX]{x1D703}_{in}$
is very close to zero, i.e. the top wall temperature. This is consistent with
![]() $Nu$
nearly having the value of the conducting case (figure 9
a). Also the bulk temperature is very close to the fully conducting case
$Nu$
nearly having the value of the conducting case (figure 9
a). Also the bulk temperature is very close to the fully conducting case
![]() $\unicode[STIX]{x1D703}=0.5$
. When
$\unicode[STIX]{x1D703}=0.5$
. When
![]() $\ell _{C}$
is decreased, making the top plate less and less conducting,
$\ell _{C}$
is decreased, making the top plate less and less conducting,
![]() $\unicode[STIX]{x1D703}_{in}$
increases gradually, reaching
$\unicode[STIX]{x1D703}_{in}$
increases gradually, reaching
![]() $\unicode[STIX]{x1D703}_{in}=0.5$
when
$\unicode[STIX]{x1D703}_{in}=0.5$
when
![]() $\ell _{C}=0.25$
. This equals the bulk temperature in a fully conducting system. However, when
$\ell _{C}=0.25$
. This equals the bulk temperature in a fully conducting system. However, when
![]() $\ell _{C}$
is decreased, also the bulk temperature gradually increases and nearly reaches 0.6 for
$\ell _{C}$
is decreased, also the bulk temperature gradually increases and nearly reaches 0.6 for
![]() $\ell _{C}=0.25$
. This rise in the bulk temperature is much slower than the rise in the temperature above the insulating area, meaning that the gradient between insulating regions at the plate and the bulk decreases and thus so does the heat transfer (see figure 9
a). Even though these simulations were conducted using only
$\ell _{C}=0.25$
. This rise in the bulk temperature is much slower than the rise in the temperature above the insulating area, meaning that the gradient between insulating regions at the plate and the bulk decreases and thus so does the heat transfer (see figure 9
a). Even though these simulations were conducted using only
![]() $f=9$
, one expects similar trends to apply for other values of
$f=9$
, one expects similar trends to apply for other values of
![]() $f$
. From the previous simulations we found that, when increasing
$f$
. From the previous simulations we found that, when increasing
![]() $f$
,
$f$
,
![]() $Nu/Nu_{fc}$
will rise and
$Nu/Nu_{fc}$
will rise and
![]() $\unicode[STIX]{x1D703}_{ins}$
will decrease. The same response can be achieved by increasing
$\unicode[STIX]{x1D703}_{ins}$
will decrease. The same response can be achieved by increasing
![]() $\ell _{C}$
as we increase the conducting area and approach the case of the fully conducting system.
$\ell _{C}$
as we increase the conducting area and approach the case of the fully conducting system.
3.4 Mixed insulating and conducting patterns in two dimensions
Until now, all the patterns that have been applied to the top and bottom boundary walls were one-dimensional (1D) stripe-like patterns. We only varied the width of the patches and the ratio between the insulating and conducting fractions. In this subsection we add an additional spatial dependence to these patterns to make them chequerboard-like:
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\unicode[STIX]{x1D703}(\hat{x},{\hat{y}},\hat{\boldsymbol{z}}=1)=0,\quad \hat{x}\in [iL_{px},L_{px1}+iL_{px}],~{\hat{y}}\in [jL_{py},L_{py1}+jL_{px}],~i,j\in \mathbb{Z},\\ \unicode[STIX]{x2202}_{z}\unicode[STIX]{x1D703}(\hat{x},{\hat{y}},\hat{\boldsymbol{z}}=1)=0,\quad \hat{x}\notin [iL_{px},L_{px1}+iL_{px}],~{\hat{y}}\notin [jL_{py},L_{py1}+jL_{px}],~i,j\in \mathbb{Z},\\ \unicode[STIX]{x1D703}(\hat{x},{\hat{y}},\hat{\boldsymbol{z}}=0)=1,\quad \forall ~\hat{x},{\hat{y}}.\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\unicode[STIX]{x1D703}(\hat{x},{\hat{y}},\hat{\boldsymbol{z}}=1)=0,\quad \hat{x}\in [iL_{px},L_{px1}+iL_{px}],~{\hat{y}}\in [jL_{py},L_{py1}+jL_{px}],~i,j\in \mathbb{Z},\\ \unicode[STIX]{x2202}_{z}\unicode[STIX]{x1D703}(\hat{x},{\hat{y}},\hat{\boldsymbol{z}}=1)=0,\quad \hat{x}\notin [iL_{px},L_{px1}+iL_{px}],~{\hat{y}}\notin [jL_{py},L_{py1}+jL_{px}],~i,j\in \mathbb{Z},\\ \unicode[STIX]{x1D703}(\hat{x},{\hat{y}},\hat{\boldsymbol{z}}=0)=1,\quad \forall ~\hat{x},{\hat{y}}.\end{array}\right\}\end{eqnarray}$$
A schematic of a set of four patches, two insulating and two conducting, is shown in figure 10. The dimensions of both types of patches were kept equal, i.e.
![]() $L_{px1}=L_{py1}=L_{px2}=L_{py2}$
, meaning
$L_{px1}=L_{py1}=L_{px2}=L_{py2}$
, meaning
![]() $\ell _{c}=1/2$
.
$\ell _{c}=1/2$
.
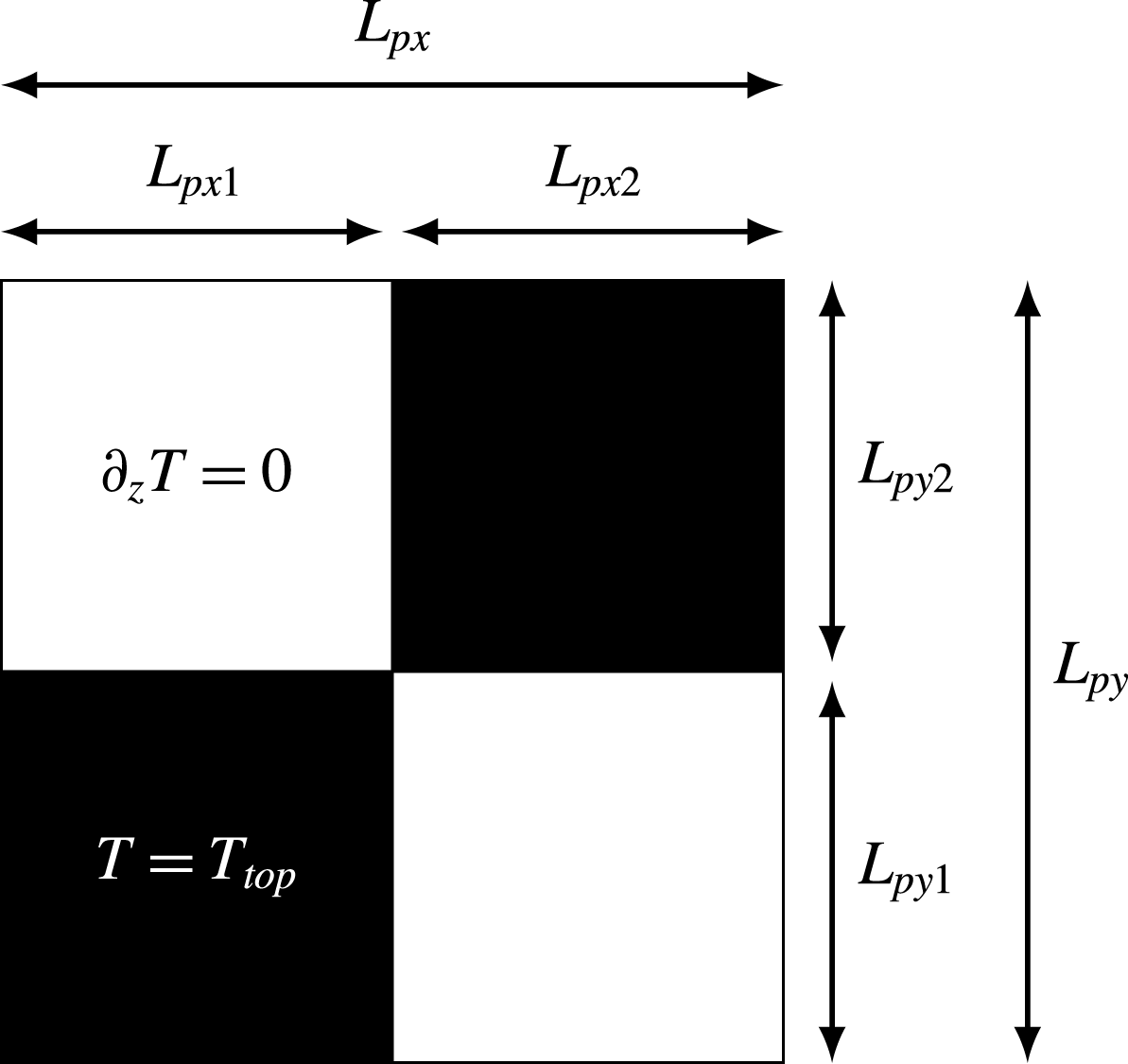
Figure 10. Top view of the top plate BCs with applied chequerboard pattern (
![]() $f=1$
). Here
$f=1$
). Here
![]() $L_{px}$
and
$L_{px}$
and
![]() $L_{py}$
are the horizontal and vertical dimensions of a set of patches. The set itself is divided into two insulating (white) and two conducting (black) areas, all with equal dimensions:
$L_{py}$
are the horizontal and vertical dimensions of a set of patches. The set itself is divided into two insulating (white) and two conducting (black) areas, all with equal dimensions:
![]() $L_{px1}=L_{py1}=L_{px2}=L_{py2}$
.
$L_{px1}=L_{py1}=L_{px2}=L_{py2}$
.
As we took both horizontal dimensions to be equal, we define a single frequency
![]() $f$
in both directions. The plate is divided into
$f$
in both directions. The plate is divided into
![]() $f$
sets of patches, which have dimensions
$f$
sets of patches, which have dimensions
![]() $L_{px}=L_{py}=L_{p}$
. When
$L_{px}=L_{py}=L_{p}$
. When
![]() $f=1$
the complete boundary consists of a single set of patches. By increasing
$f=1$
the complete boundary consists of a single set of patches. By increasing
![]() $f$
to 2, the plate will consist of four sets of four patches each. To give a further impression how the temperature fields resulting from these BCs look, two visualizations of instantaneous temperature fields for
$f$
to 2, the plate will consist of four sets of four patches each. To give a further impression how the temperature fields resulting from these BCs look, two visualizations of instantaneous temperature fields for
![]() $f=4$
and
$f=4$
and
![]() $f=20$
are shown in figure 11. The visualizations show respectively 16 and 400 sets of patches, which each consist of two insulating and two conducting areas.
$f=20$
are shown in figure 11. The visualizations show respectively 16 and 400 sets of patches, which each consist of two insulating and two conducting areas.
Figure 12(a) shows the normalized Nusselt number
![]() $Nu/Nu_{fc}$
for the 1D (stripe) and 2D (chequerboard) patterns as a function of
$Nu/Nu_{fc}$
for the 1D (stripe) and 2D (chequerboard) patterns as a function of
![]() $k_{x}$
. For these cases,
$k_{x}$
. For these cases,
![]() $Ra=10^{8}$
,
$Ra=10^{8}$
,
![]() $\mathit{Pr}=1$
and the error bars indicate the statistical convergence error. At first sight, the heat transfer is not that different when applying 1D or 2D patterning. At the lowest division, where we have divided the system into two or four areas for the 1D and 2D case, respectively, the difference is negligible. Also at the highest value of
$\mathit{Pr}=1$
and the error bars indicate the statistical convergence error. At first sight, the heat transfer is not that different when applying 1D or 2D patterning. At the lowest division, where we have divided the system into two or four areas for the 1D and 2D case, respectively, the difference is negligible. Also at the highest value of
![]() $k_{x}$
, the difference is inside statistical errors and seems insignificant.
$k_{x}$
, the difference is inside statistical errors and seems insignificant.
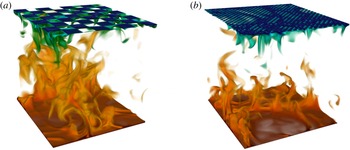
Figure 11. Two 3D visualizations of the instantaneous temperature field with different pattern frequencies at the top boundary. Hot fluid is shown in red while the cool fluid has a blue colour. For both visualizations,
![]() $Ra=10^{8}$
and
$Ra=10^{8}$
and
![]() $\mathit{Pr}=1$
. (a) Visualization with
$\mathit{Pr}=1$
. (a) Visualization with
![]() $f=4$
, which results in 16 sets of patches each containing two insulating patches and two conducting patches. (b) Visualization with
$f=4$
, which results in 16 sets of patches each containing two insulating patches and two conducting patches. (b) Visualization with
![]() $f=20$
, which results in 400 sets of patches. Hot plumes rise from the bottom plate while cold plumes are ejected from the top boundary.
$f=20$
, which results in 400 sets of patches. Hot plumes rise from the bottom plate while cold plumes are ejected from the top boundary.
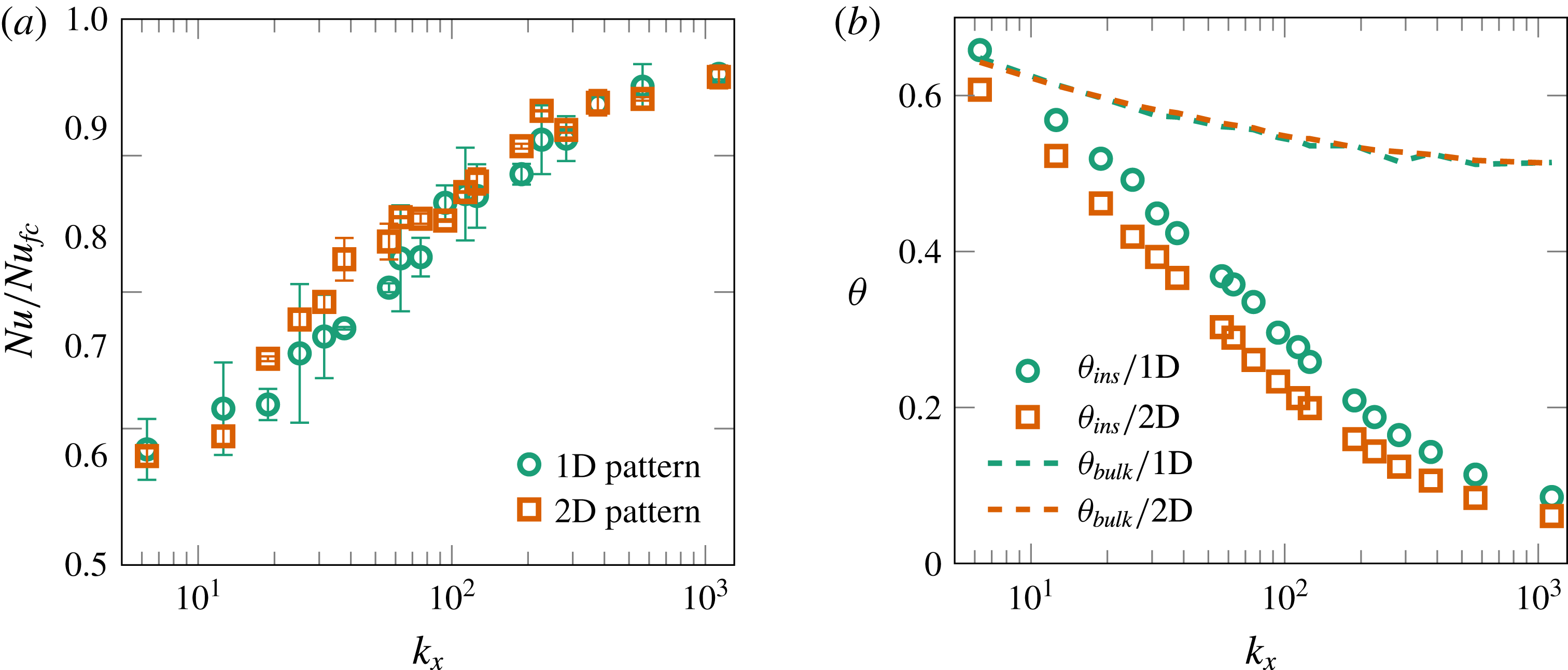
Figure 12. (a) Normalized Nusselt number
![]() $Nu/Nu_{fc}$
for 1D and 2D patterning versus
$Nu/Nu_{fc}$
for 1D and 2D patterning versus
![]() $k_{x}$
for
$k_{x}$
for
![]() $Ra=10^{8}$
and
$Ra=10^{8}$
and
![]() $\mathit{Pr}=1$
. The error bars show the statistical convergence error. (b) Average temperature
$\mathit{Pr}=1$
. The error bars show the statistical convergence error. (b) Average temperature
![]() $\unicode[STIX]{x1D703}_{in}$
just below the insulating area and average bulk temperature
$\unicode[STIX]{x1D703}_{in}$
just below the insulating area and average bulk temperature
![]() $\unicode[STIX]{x1D703}_{bu}$
, both as a function of
$\unicode[STIX]{x1D703}_{bu}$
, both as a function of
![]() $k_{x}$
for the 1D and 2D patternings. The
$k_{x}$
for the 1D and 2D patternings. The
![]() $Ra$
and
$Ra$
and
![]() $\mathit{Pr}$
values are the same as for panel (a).
$\mathit{Pr}$
values are the same as for panel (a).
At first glance, the 1D stripe pattern and the 2D chequerboard pattern may seem idealized representations. However, all other stripe and rectangular chequerboard patterns fall within these extreme cases, as the stripe pattern has
![]() $L_{px}/L_{py}\rightarrow \infty$
(or conversely
$L_{px}/L_{py}\rightarrow \infty$
(or conversely
![]() $\rightarrow 0$
), while for the chequerboard pattern
$\rightarrow 0$
), while for the chequerboard pattern
![]() $L_{px}/L_{py}=1$
. Our work shows that, for the relatively small wavelengths considered here, the shape of these patterns does not have a significant influence on the flow dynamics. While we do not expect
$L_{px}/L_{py}=1$
. Our work shows that, for the relatively small wavelengths considered here, the shape of these patterns does not have a significant influence on the flow dynamics. While we do not expect
![]() $\ell _{C}$
to affect this statement considerably, larger wavelength patterns could show some dependence on their shape. In the experiments of Wang et al. (Reference Wang, Huang and Xia2017), the patches have wavelengths comparable to the system height and their distribution considerably affects the flow structure. Here, we consider wavelengths that are much smaller, affecting the flow only below the thermal boundary layer thickness, and reducing the Nusselt number. The largest wavelength considered in this work is still smaller than the smallest wavelength in the rectangular tank of Wang et al. (Reference Wang, Huang and Xia2017). There appear to be two clear regimes: the large patch regime, which shows a clear influence on the flow dynamics and whose effect is likely to be shape-dependent, and the small patch regime, which only affects the boundary layers and thus the heat transfer. While there must exist a cross-over regime between the two, it appears to be just outside the wavelengths we are considering.
$\ell _{C}$
to affect this statement considerably, larger wavelength patterns could show some dependence on their shape. In the experiments of Wang et al. (Reference Wang, Huang and Xia2017), the patches have wavelengths comparable to the system height and their distribution considerably affects the flow structure. Here, we consider wavelengths that are much smaller, affecting the flow only below the thermal boundary layer thickness, and reducing the Nusselt number. The largest wavelength considered in this work is still smaller than the smallest wavelength in the rectangular tank of Wang et al. (Reference Wang, Huang and Xia2017). There appear to be two clear regimes: the large patch regime, which shows a clear influence on the flow dynamics and whose effect is likely to be shape-dependent, and the small patch regime, which only affects the boundary layers and thus the heat transfer. While there must exist a cross-over regime between the two, it appears to be just outside the wavelengths we are considering.
When we look at
![]() $\unicode[STIX]{x1D703}_{in}$
, the temperature just below the insulating region in figure 12(b), we see a similar trend. The temperature below the insulating region is on average always lower for the 2D pattern. This is even the case for the higher and lower limits of
$\unicode[STIX]{x1D703}_{in}$
, the temperature just below the insulating region in figure 12(b), we see a similar trend. The temperature below the insulating region is on average always lower for the 2D pattern. This is even the case for the higher and lower limits of
![]() $k_{x}$
. The heat can escape towards a conducting region in any direction, while for stripes it can only escape in one direction. Thus, the distance to a sink is smaller and thus the temperature is smaller. The bulk temperatures for both the 1D and 2D cases are almost identical, which means that the change in pattern has no effect on this quantity. From these results we can conclude that the impact of the two different patterns is very similar, and the quantitative differences between stripe and chequerboard patterns are at most small.
$k_{x}$
. The heat can escape towards a conducting region in any direction, while for stripes it can only escape in one direction. Thus, the distance to a sink is smaller and thus the temperature is smaller. The bulk temperatures for both the 1D and 2D cases are almost identical, which means that the change in pattern has no effect on this quantity. From these results we can conclude that the impact of the two different patterns is very similar, and the quantitative differences between stripe and chequerboard patterns are at most small.
4 Summary and conclusions
A series of DNS of turbulent RB convection using mixed conducting and insulating BCs were conducted. First, we applied a stripe-like pattern on the top boundary and varied the amount of stripes while keeping the conduction–insulation ratio constant at
![]() $\ell _{C}=1/2$
. When the top plate is divided in half,
$\ell _{C}=1/2$
. When the top plate is divided in half,
![]() $Nu$
has a value of approximately two-thirds of that for the fully conducting case. By increasing the frequency of the pattern,
$Nu$
has a value of approximately two-thirds of that for the fully conducting case. By increasing the frequency of the pattern,
![]() $Nu$
also increases, with a maximum value very close to that as if it were fully conducting. With only half the effective conducting area on the top plate, when applying a dense pattern, the effect of the insulating patches almost completely vanishes. An increase in
$Nu$
also increases, with a maximum value very close to that as if it were fully conducting. With only half the effective conducting area on the top plate, when applying a dense pattern, the effect of the insulating patches almost completely vanishes. An increase in
![]() $Ra$
results only in a marginal decrease in
$Ra$
results only in a marginal decrease in
![]() $Nu/Nu_{fc}$
for the largest
$Nu/Nu_{fc}$
for the largest
![]() $f$
. This shift towards the fully conducting efficiency as seen with the Nusselt number when increasing the pattern frequency is also visible in
$f$
. This shift towards the fully conducting efficiency as seen with the Nusselt number when increasing the pattern frequency is also visible in
![]() $\unicode[STIX]{x1D703}_{bulk}$
and
$\unicode[STIX]{x1D703}_{bulk}$
and
![]() $\unicode[STIX]{x1D703}_{ins}$
.
$\unicode[STIX]{x1D703}_{ins}$
.
Using a 2D Fourier transform, calculated from a horizontal slice of the instantaneous temperature, it is possible to identify the imprint of the BCs inside the flow. By comparing different spectra, each calculated from a horizontal slice slightly further away from the top boundary wall, the penetration depth of the BCs inside the flow was investigated. The imprint of the striped pattern slowly fades away when moving from the top wall towards the border of the thermal boundary layer. Outside of the thermal boundary layer the imprint has completely vanished, even for the extreme case
![]() $f=1$
. The thermal boundary layer masks the actual boundary, including all insulating imperfections, and presents a new effective boundary to the bulk flow. In the thermal boundary layer, the heat is conducted to the conducting areas. This transport is more efficient when the pattern frequency is large. A lower Rayleigh number increases the thickness of the boundary layer and thereby also increases the effectiveness of the heat transport.
$f=1$
. The thermal boundary layer masks the actual boundary, including all insulating imperfections, and presents a new effective boundary to the bulk flow. In the thermal boundary layer, the heat is conducted to the conducting areas. This transport is more efficient when the pattern frequency is large. A lower Rayleigh number increases the thickness of the boundary layer and thereby also increases the effectiveness of the heat transport.
Extending the pattern to both the top and bottom boundary wall resulted in similar behaviour for the heat transfer and the average temperature below the insulating area. The primary difference is for the lowest pattern frequency where we practically have only half an RB cell and we find a Nusselt number with half the value of the fully conducting case. Adding an additional dimension to the pattern, creating a chequerboard-like pattern, also did not change the behaviour significantly.
Our results demonstrate that small and even large imperfections in the temperature BCs are barely felt in the system dynamics in terms of global heat transfer and local temperature measurements. Only in extreme cases as a half-and-half conducting and adiabatic plate was the effect significant. The effect of imperfect temperature BCs of fully turbulent RB is weaker than the effects of velocity BCs in 2D RB (van der Poel et al. Reference van der Poel, Ostilla-Mónico, Verzicco and Lohse2014), or the effect of rough elements near the boundaries (Tisserand et al. Reference Tisserand, Creyssels, Gasteuil, Pabiou, Gibert, Castating and Chilla2011). It is not yet clear if these boundary imperfections lead to significant changes in the dynamics of the bulk flow and this remains an open question for future works. Going beyond the scope of the present paper, we mention that the simulations by Cooper et al. (Reference Cooper, Moresi and Lenardic2013) and the experiments by Wang et al. (Reference Wang, Huang and Xia2017) show that, with even larger adiabatic patches, changes in the flow topology can happen due to the arrangement of patches. The patches can also be varied in time, which is a way to control the bulk temperature or to fine tune the heat transfer, which is relevant for many industrial applications. In another work Whitehead & Behn (Reference Whitehead and Behn2015) showed that the combination of shear and mixed BCs could also play a critical role in the system dynamics. Understanding the deeper reasons for this behaviour may lead to better models for natural convection for geophysically and astrophysically relevant flows.
Acknowledgements
We thank L. Biferale for his role in motivating this paper. We also thank V. Spandan, Y. Yang and X. Zhu for fruitful discussions. D.B. and E.P.v.d.P. were funded by FOM grants, and R.O.-M. was funded by an ERC Advanced Grant. Computing time at the Dutch supercomputer Cartesius comes from a NWO grant.
Appendix A. Numerical details
Data from numerical simulations are contained in tables 1–4.
Table 1. Nusselt and Rayleigh numbers for various
![]() $f$
and the fully conducting case (fc), with
$f$
and the fully conducting case (fc), with
![]() $Pr=1$
and
$Pr=1$
and
![]() $\ell _{c}=1/2$
, used in figure 3(a,b).
$\ell _{c}=1/2$
, used in figure 3(a,b).

Table 2. Data from all numerical simulations for the single-sided mixed BCs and the fully conducting case, used in figures 4(a), 5(a), 5(b) and 8(b). The fc in the
![]() $f$
column indicates the fully conducting case, e.g. without the striped pattern.
$f$
column indicates the fully conducting case, e.g. without the striped pattern.
Table 3. Data from all numerical simulations for the double-sided mixed BCs, with
![]() $Ra=10^{8}$
,
$Ra=10^{8}$
,
![]() $Pr=1$
and
$Pr=1$
and
![]() $\ell _{c}=1/2$
, used in figure 8(a,b).
$\ell _{c}=1/2$
, used in figure 8(a,b).

Table 4. Data from all numerical simulations of the chequerboard pattern, with
![]() $Ra=10^{8}$
,
$Ra=10^{8}$
,
![]() $Pr=1$
and
$Pr=1$
and
![]() $\ell _{c}=1/2$
, used in figure 12(a,b).
$\ell _{c}=1/2$
, used in figure 12(a,b).