Article contents
Mixing in a vortex breakdown flow
Published online by Cambridge University Press: 14 August 2013
Abstract
In this paper we present experimental and theoretical results on the mixing inside a cylinder with a rotating lid. The helical flow that is created by the rotation of the disc is well known to exhibit a vortex breakdown bubble over a finite range of Reynolds numbers. The mixing properties of the flow are analysed quantitatively by measuring the exponential decay of the variance as a function of time. This homogenization time is extremely sensitive to the asymmetries of the flow, which are introduced by tilting the rotating or the stationary disc and accurately measured using particle image velocimetry (PIV). In the absence of vortex breakdown, the homogenization time is strongly decreased (by a factor of 10) with only a moderate tilt angle of the rotating lid (of the order of 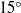 $1{5}^{\circ } $ ). This phenomenon can be explained by the presence of small radial jets at the periphery which create a strong convective mixing. A simple model of exchange flow between the periphery and the bulk correctly predicts the scaling laws for the homogenization time. In the presence of vortex breakdown, the scalar is trapped inside the vortex breakdown bubble, and thus increases substantially the time needed for homogenization. Curiously, the tilt of the rotating lid has a weak effect on the mixing, but a small tilt of the stationary disc (of the order of
$1{5}^{\circ } $ ). This phenomenon can be explained by the presence of small radial jets at the periphery which create a strong convective mixing. A simple model of exchange flow between the periphery and the bulk correctly predicts the scaling laws for the homogenization time. In the presence of vortex breakdown, the scalar is trapped inside the vortex breakdown bubble, and thus increases substantially the time needed for homogenization. Curiously, the tilt of the rotating lid has a weak effect on the mixing, but a small tilt of the stationary disc (of the order of 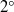 ${2}^{\circ } $ ) strongly decreases (by a factor of 10) the homogenization time. Even more surprising is that the homogenization time diverges when the size of the bubble vanishes. All of these features are recovered by applying the Melnikov theory to calculate the volume of the lobes that exit the bubble. It is the first time that this technique has been applied to a three-dimensional stationary flow with a non-axisymmetric perturbation and compared with experimental results, although it has been applied often to two-dimensional flows with a periodic perturbation.
${2}^{\circ } $ ) strongly decreases (by a factor of 10) the homogenization time. Even more surprising is that the homogenization time diverges when the size of the bubble vanishes. All of these features are recovered by applying the Melnikov theory to calculate the volume of the lobes that exit the bubble. It is the first time that this technique has been applied to a three-dimensional stationary flow with a non-axisymmetric perturbation and compared with experimental results, although it has been applied often to two-dimensional flows with a periodic perturbation.
Information
- Type
- Papers
- Information
- Copyright
- ©2013 Cambridge University Press
References
- 10
- Cited by

