Article contents
Moving contact line dynamics: from diffuse to sharp interfaces
Published online by Cambridge University Press: 22 December 2015
Abstract
We reconcile two scaling laws that have been proposed in the literature for the slip length associated with a moving contact line in diffuse interface models, by demonstrating each to apply in a different regime of the ratio of the microscopic interfacial width 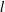 $l$ and the macroscopic diffusive length
$l$ and the macroscopic diffusive length 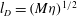 $l_{D}=(M{\it\eta})^{1/2}$ , where
$l_{D}=(M{\it\eta})^{1/2}$ , where 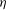 ${\it\eta}$ is the fluid viscosity and
${\it\eta}$ is the fluid viscosity and 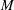 $M$ the mobility governing intermolecular diffusion. For small
$M$ the mobility governing intermolecular diffusion. For small 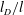 $l_{D}/l$ we find a diffuse interface regime in which the slip length scales as
$l_{D}/l$ we find a diffuse interface regime in which the slip length scales as 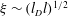 ${\it\xi}\sim (l_{D}l)^{1/2}$ . For larger
${\it\xi}\sim (l_{D}l)^{1/2}$ . For larger 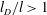 $l_{D}/l>1$ we find a sharp interface regime in which the slip length depends only on the diffusive length,
$l_{D}/l>1$ we find a sharp interface regime in which the slip length depends only on the diffusive length, 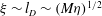 ${\it\xi}\sim l_{D}\sim (M{\it\eta})^{1/2}$ , and therefore only on the macroscopic variables
${\it\xi}\sim l_{D}\sim (M{\it\eta})^{1/2}$ , and therefore only on the macroscopic variables 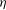 ${\it\eta}$ and
${\it\eta}$ and 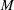 $M$ , independent of the microscopic interfacial width
$M$ , independent of the microscopic interfacial width 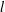 $l$ . We also give evidence that modifying the microscopic interfacial terms in the model’s free energy functional appears to affect the value of the slip length only in the diffuse interface regime, consistent with the slip length depending only on macroscopic variables in the sharp interface regime. Finally, we demonstrate the dependence of the dynamic contact angle on the capillary number to be in excellent agreement with the theoretical prediction of Cox (J. Fluid Mech., vol. 168, 1986, p. 169), provided we allow the slip length to be rescaled by a dimensionless prefactor. This prefactor appears to converge to unity in the sharp interface limit, but is smaller in the diffuse interface limit. The excellent agreement of results obtained using three independent numerical methods, across several decades of the relevant dimensionless variables, demonstrates our findings to be free of numerical artefacts.
$l$ . We also give evidence that modifying the microscopic interfacial terms in the model’s free energy functional appears to affect the value of the slip length only in the diffuse interface regime, consistent with the slip length depending only on macroscopic variables in the sharp interface regime. Finally, we demonstrate the dependence of the dynamic contact angle on the capillary number to be in excellent agreement with the theoretical prediction of Cox (J. Fluid Mech., vol. 168, 1986, p. 169), provided we allow the slip length to be rescaled by a dimensionless prefactor. This prefactor appears to converge to unity in the sharp interface limit, but is smaller in the diffuse interface limit. The excellent agreement of results obtained using three independent numerical methods, across several decades of the relevant dimensionless variables, demonstrates our findings to be free of numerical artefacts.
Information
- Type
- Papers
- Information
- Copyright
- © 2016 Cambridge University Press
References
- 48
- Cited by


