Hostname: page-component-76fb5796d-wq484 Total loading time: 0 Render date: 2024-04-25T12:29:09.965Z Has data issue: false hasContentIssue false
  • English
  • Français

A multifractal model for the momentum transfer process in wall-bounded flows

Published online by Cambridge University Press:  05 July 2017

X. I. A. Yang Open the ORCID record for X. I. A. Yang [Opens in a new window]  and
A. Lozano-Durán
X. I. A. Yang*
Affiliation:
Center for Turbulence Research, Stanford, 94305, USA
A. Lozano-Durán
Affiliation:
Center for Turbulence Research, Stanford, 94305, USA
*
†Email address for correspondence: xiangyang@stanford.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

The cascading process of turbulent kinetic energy from large-scale fluid motions to small-scale and lesser-scale fluid motions in isotropic turbulence may be modelled as a hierarchical random multiplicative process according to the multifractal formalism. In this work, we show that the same formalism might also be used to model the cascading process of momentum in wall-bounded turbulent flows. However, instead of being a multiplicative process, the momentum cascade process is additive. 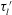The proposed multifractal model is used for describing the flow kinematics of the low-pass filtered streamwise wall-shear stress fluctuation $\unicode[STIX]{x1D70F}_{l}^{\prime }$, where 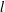$l$ is the filtering length scale. According to the multifractal formalism, 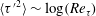$\langle {\unicode[STIX]{x1D70F}^{\prime }}^{2}\rangle \sim \log (Re_{\unicode[STIX]{x1D70F}})$ and 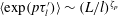$\langle \exp (p\unicode[STIX]{x1D70F}_{l}^{\prime })\rangle \sim (L/l)^{\unicode[STIX]{x1D701}_{p}}$ in the log-region, where 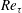$Re_{\unicode[STIX]{x1D70F}}$ is the friction Reynolds number, 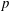$p$ is a real number, 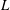$L$ is an outer length scale and 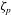$\unicode[STIX]{x1D701}_{p}$ is the anomalous exponent of the momentum cascade. These scalings are supported by the data from a direct numerical simulation of channel flow at 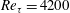$Re_{\unicode[STIX]{x1D70F}}=4200$.

JFM classification

Turbulent Flows: Turbulence theory Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulent Flows
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 824 , 10 August 2017 , R2
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alfredsson, P. H., Johansson, A. V., Haritonidis, J. H. & Eckelmann, H. 1988 The fluctuating wall-shear stress and the velocity field in the viscous sublayer. Phys. Fluids 31 (5), 1026–1033.Google Scholar
Aoyama, T., Ishihara, T., Kaneda, Y., Yokokawa, M. & Uno, A. 2005 Statistics of energy transfer in high-resolution direct numerical simulation of turbulence in a periodic box. J. Phys. Soc. Japan 74, 3202–3212.Google Scholar
Baars, W. J., Hutchins, N. & Marusic, I. 2017 Reynolds number trend of hierarchies and scale interactions in turbulent boundary layers. Phil. Trans. R. Soc. Lond. 375, 2089.Google Scholar
Batchelor, G. K. 1953 The Theory of Homogeneous Turbulence. Cambridge University Press.Google Scholar
Benzi, R., Ciliberto, S., Tripiccione, R., Baudet, C., Massaioli, F. & Succi, S. 1993 Extended self-similarity in turbulent flows. Phys. Rev. E 48 (1), R29.Google Scholar
Biferale, L. 2003 Shell models of energy cascade in turbulence. Annu. Rev. Fluid Mech. 35 (1), 441–468.Google Scholar
Cardesa, J. I., Vela-Martín, A., Dong, S. & Jiménez, J. 2015 The temporal evolution of the energy flux across scales in homogeneous turbulence. Phys. Fluids 27 (11), 111702.Google Scholar
Del Álamo, J. C., Jimenez, J., Zandonade, P. & Moser, R. D. 2006 Self-similar vortex clusters in the turbulent logarithmic region. J. Fluid Mech. 561, 329–358.Google Scholar
Flores, O. & Jiménez, J. 2010 Hierarchy of minimal flow units in the logarithmic layer. Phys. Fluids 22 (7), 071704.Google Scholar
Frisch, U. & Donnelly, R. J. 1996 Turbulence: The Legacy of AN Kolmogorov. AIP.Google Scholar
Frisch, U., Sulem, P.-L. & Nelkin, M. 1978 A simple dynamical model of intermittent fully developed turbulence. J. Fluid Mech. 87 (04), 719–736.Google Scholar
Goto, S. 2012 Coherent structures and energy cascade in homogeneous turbulence. Progress of Theoretical Physics Supplement 195, 139–156.Google Scholar
Heisenberg, W. 1985 On the theory of statistical and isotropic turbulence. In Original Scientific Papers Wissenschaftliche Originalarbeiten, pp. 115–119. Springer.Google Scholar
Jiménez, J. 2012 Cascades in wall-bounded turbulence. Annu. Rev. Fluid Mech. 44, 27–45.Google Scholar
Jiménez, J.2016 Optimal fluxes and Reynolds stresses. arXiv:1606.02160.Google Scholar
Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.CrossRefGoogle Scholar
Kolmogorov, A. N. 1941 The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Dokl. Akad. Nauk SSSR 30, 301–305.Google Scholar
Kolmogorov, A. N. 1962 A refinement of previous hypotheses concerning the local structure of turbulence in a viscous incompressible fluid at high Reynolds number. J. Fluid Mech. 13 (01), 82–85.Google Scholar
Kraichnan, R. H. 1965 Lagrangian-history closure approximation for turbulence. Phys. Fluids 8 (4), 575–598.Google Scholar
Kraichnan, R. H. 1991 Stochastic modeling of isotropic turbulence. In New Perspectives in Turbulence, pp. 1–54. Springer.Google Scholar
Krug, D., Yang, X. I. A., de Silva, C. M., Ostilla-Monico, R., Verzicco, R., Marusic, I. & Lohse, D. 2017 Statistics of turbulence in the energy-containing range of Taylor–Couette compared to canonical wall-bounded flows. J. Fluid Mech. (submitted).Google Scholar
Landau, L. & Lifshitz, E. 1987 Fluid mechanics. In Course of Theoretical Physics. Pergamon.Google Scholar
Lee, M. & Moser, R. D. 2015 Direct numerical simulation of turbulent channel flow up to Re 𝜏 ≈ 5200. J. Fluid Mech. 774, 395–415.Google Scholar
Leith, C. E. 1967 Diffusion approximation to inertial energy transfer in isotropic turbulence. Phys. Fluids 10, 1409–1416.Google Scholar
Leung, T., Swaminathan, N. & Davidson, P. 2012 Geometry and interaction of structures in homogeneous isotropic turbulence. J. Fluid Mech. 710, 453–481.Google Scholar
Lozano-Durán, A., Flores, O. & Jiménez, J. 2012 The three-dimensional structure of momentum transfer in turbulent channels. J. Fluid Mech. 694, 100–130.Google Scholar
Lozano-Durán, A., Holzner, M. & Jiménez, J. 2016 Multiscale analysis of the topological invariants in the logarithmic region of turbulent channels at a friction Reynolds number of 932. J. Fluid Mech. 803, 356–394.Google Scholar
Lozano-Durán, A. & Jiménez, J. 2014a Effect of the computational domain on direct simulations of turbulent channels up to Re 𝜏 = 4200. Phys. Fluids 26 (1), 011702.Google Scholar
Lozano-Durán, A. & Jiménez, J. 2014b Time-resolved evolution of coherent structures in turbulent channels: characterization of eddies and cascades. J. Fluid Mech. 759, 432–471.Google Scholar
Mandelbrot, B. B. 1972 Possible refinement of the lognormal hypothesis concerning the distribution of energy dissipation in intermittent turbulence. In Statistical Models and Turbulence, pp. 333–351. Springer.CrossRefGoogle Scholar
Mandelbrot, B. B. 1999 Intermittent turbulence in self-similar cascades: divergence of high moments and dimension of the carrier. In Multifractals and Noise, pp. 317–357. Springer.Google Scholar
Marusic, I., Monty, J. P., Hultmark, M. & Smits, A. J. 2013 On the logarithmic region in wall turbulence. J. Fluid Mech. 716, R3.Google Scholar
Marusic, I. & Perry, A. 1995 A wall-wake model for the turbulence structure of boundary layers. Part 2. Further experimental support. J. Fluid Mech. 298, 389–407.CrossRefGoogle Scholar
Mathis, R., Marusic, I., Chernyshenko, S. I. & Hutchins, N. 2013 Estimating wall-shear-stress fluctuations given an outer region input. J. Fluid Mech. 715, 163–180.Google Scholar
Meneveau, C. & Katz, J. 2000 Scale-invariance and turbulence models for large-eddy simulation. Annu. Rev. Fluid Mech. 32 (1), 1–32.Google Scholar
Meneveau, C., Lund, T. S. & Cabot, W. H. 1996 A Lagrangian dynamic subgrid-scale model of turbulence. J. Fluid Mech. 319, 353–385.Google Scholar
Meneveau, C. & Sreenivasan, K. 1987 Simple multifractal cascade model for fully developed turbulence. Phys. Rev. Lett. 59 (13), 1424–1427.Google Scholar
Meneveau, C. & Sreenivasan, K. 1991 The multifractal nature of turbulent energy dissipation. J. Fluid Mech. 224, 429–484.Google Scholar
Morrill-Winter, C., Philip, J. & Klewicki, J. 2017 Statistical evidence of anasymptotic geometric structure to the momentum transporting motions in turbulent boundary layers. Phil. Trans. R. Soc. Lond. A 375 (2089), 20160084.Google Scholar
Obukhov, A. M. 1941 On the distribution of energy in the spectrum of turbulent flow. Izv. Akad. Nauk SSSR Geogr. Geofiz. 5 (4), 453–466.Google Scholar
O’Neil, J. & Meneveau, C. 1993 Spatial correlations in turbulence: predictions from the multifractal formalism and comparison with experiments. Phys. Fluids A 5 (1), 158–172.Google Scholar
Onsager, L. 1949 Statistical hydrodynamics. Il Nuovo Cimento 6, 279–287.Google Scholar
Orszag, S. A. 1970 Analytical theories of turbulence. J. Fluid Mech. 41, 363–386.Google Scholar
Österlund, J. M. 1999 Experimental Studies of Zero Pressure-Gradient Turbulent Boundary Layer Flow. Royal Institute of Technology, Department of Mechanics.Google Scholar
Park, G. I. & Moin, P. 2016 Space-time characteristics of wall-pressure and wall shear-stress fluctuations in wall-modeled large eddy simulation. Phys. Rev. Fluids 1 (2), 024404.Google Scholar
Park, G. I., Wallace, J. M., Wu, X. & Moin, P. 2012 Boundary layer turbulence in transitional and developed states. Phys. Fluids 24 (3), 035105.Google Scholar
Perry, A. E. & Chong, M. S. 1982 On the mechanism of wall turbulence. J. Fluid Mech. 119, 173–217.Google Scholar
Piomelli, U. & Balaras, E. 2002 Wall-layer models for large-eddy simulations. Annu. Rev. Fluid Mech. 34 (1), 349–374.Google Scholar
Piomelli, U., Cabot, W. H., Moin, P. & Lee, S. 1991 Subgrid-scale backscatter in turbulent and transitional flows. Phys. Fluids A 3 (7), 1766–1771.Google Scholar
Pope, S. B. 2001 Turbulent Flows. IOP Publishing.Google Scholar
Richardson, L. F. 1922 Weather Prediction by Numerical Process. Cambridge University Press.Google Scholar
Saddoughi, S. G. & Veeravalli, S. V. 1994 Local isotropy in turbulent boundary layers at high Reynolds number. J. Fluid Mech. 268, 333–372.CrossRefGoogle Scholar
Schlatter, P. & Örlü, R. 2010 Assessment of direct numerical simulation data of turbulent boundary layers. J. Fluid Mech. 659, 116–126.Google Scholar
de Silva, C., Marusic, I., Woodcock, J. & Meneveau, C. 2015 Scaling of second-and higher-order structure functions in turbulent boundary layers. J. Fluid Mech. 769, 654–686.Google Scholar
Townsend, A. A. 1980 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
Vinuesa, R., Duncan, R. D. & Nagib, H. M. 2016 Alternative interpretation of the superpipe data and motivation for ciclope: the effect of a decreasing viscous length scale. Eur. J. Mech. (B/Fluids) 58, 109–116.Google Scholar
Yang, X. I. A., Marusic, I. & Meneveau, C. 2016a Hierarchical random additive process and logarithmic scaling of generalized high order, two-point correlations in turbulent boundary layer flow. Phys. Rev. Fluids 1 (2), 024402.CrossRefGoogle Scholar
Yang, X. I. A., Marusic, I. & Meneveau, C. 2016b Moment generating functions and scaling laws in the inertial layer of turbulent wall-bounded flows. J. Fluid Mech. 791, R2.Google Scholar
Yang, X. I. A., Meneveau, C., Marusic, I. & Biferale, L. 2016c Extended self-similarity in moment-generating-functions in wall-bounded turbulence at high Reynolds number. Phys. Rev. Fluids 1 (4), 044405.Google Scholar