1. Introduction
A large body of research in the last 10 years has demonstrated unequivocally that the construction of accurate and efficient numerical models of hydraulic fractures benefits from embedding the tip asymptotic behaviour, which is appropriate for the discretization length of the computational grid (Adachi & Detournay Reference Adachi and Detournay2008; Peirce & Detournay Reference Peirce and Detournay2008; Lecampion et al. Reference Lecampion2013; Peirce Reference Peirce2015, Reference Peirce2016). Hitherto, research has focused on the simulation of a propagating fracture. Nonetheless, there is considerable interest in modelling the deflation of hydraulic fractures once injection has ceased, as they evolve through successive phases of arrest and recession following propagation. The main motivation for this work is to provide a more rigorous framework to interpret the decline of the borehole pressure during deflation of the fracture, either to determine the leak-off coefficient (Nolte Reference Nolte1979, Reference Nolte1986) or to estimate accurately the minimum in situ stress (Zoback et al. Reference Zoback, Rummel, Jung and Raleigh1977; Haimson Reference Haimson1989; Hayashi & Haimson Reference Hayashi and Haimson1991; Plahn et al. Reference Plahn, Nolte, Thompson and Miska1997; Sano et al. Reference Sano, Ito, Hirata and Mizuta2005; Fjær et al. Reference Fjær, Holt, Horsrud, Raaen and Risnes2008; Lakirouhani, Detournay & Bunger Reference Lakirouhani, Detournay and Bunger2016).
In this paper, we describe the construction of multiscale tip asymptotes for deflating fractures in permeable elastic media, when the front is either at rest or receding. When combined with an algorithm to simulate an evolving hydraulic fracture, these asymptotes make it possible to compute accurately not only the stress intensity factor as it declines when the front is at rest until it eventually vanishes at the transition between arrest and recession, but also the negative front velocity during recession. The asymptotes are derived by analysing the stationary solution of a semi-infinite hydraulic fracture either at rest or steadily receding, using an approach similar to the one used to construct the tip asymptotes for a propagating fracture (Desroches et al. Reference Desroches, Detournay, Lenoach, Papanastasiou, Pearson, Thiercelin and Cheng1994; Lenoach Reference Lenoach1995; Garagash & Detournay Reference Garagash and Detournay2000; Garagash, Detournay & Adachi Reference Garagash, Detournay and Adachi2011; Dontsov & Peirce Reference Dontsov and Peirce2015; Dontsov Reference Dontsov2016; Dontsov & Kresse Reference Dontsov and Kresse2018; Moukhtari & Lecampion Reference Moukhtari and Lecampion2018; Lecampion & Zia Reference Lecampion and Zia2019).
The paper is structured as follows. First, the governing equations are summarized within the context of a semi-infinite fracture. Salient features of the tip asymptotics near the end of the propagation phase are then reviewed. Next, we determine successively, through a local eigenvalue analysis, the singular asymptotes that develop closest to the fracture tip during arrest, at the transition between arrest and recession, and during recession. We then construct the multiscale asymptotes that control the development of singular boundary layers at the tip, either at the end of the arrest phase or at the beginning of recession. Implementation of these multiscale asymptotes in a numerical code is briefly discussed. Finally, an argument based on the tip asymptotics, about the inability of a fracture to recede in an impermeable medium, is described in Appendix A.
2. Governing equations for a semi-infinite hydraulic fracture
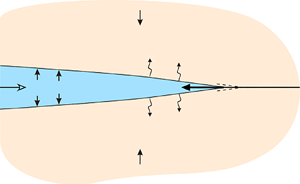
Here, we consider the problem of a semi-infinite hydraulic fracture that is either travelling at a constant velocity 
$V$ or at rest in an infinite permeable elastic medium; see figure 1. The velocity 
$V$ is taken as positive if the fracture is advancing and thus creating new solid surfaces, and negative if the fracture is receding, thus closing previously created solid surfaces at the tip. There is a far-field uniform compressive stress 
$\sigma _{0}$ normal to the fracture. Fluid is leaking from the fracture into the solid medium. The solution to this idealized problem can actually be understood as capturing the asymptotics in the vicinity of the crack front of a finite hydraulic fracture.
Figure 1. Receding tip of a deflating hydraulic fracture.
Although the tip asymptotics are critically dependent on the nature of the leak-off in propagating fractures, it is not the case for fractures that are either at rest or receding. Indeed, leak-off can be singular at the tip of an advancing fracture only under conditions of linear flow, when a Carter-type leak-off prevails (Lenoach Reference Lenoach1995; Garagash et al. Reference Garagash, Detournay and Adachi2011); otherwise, leak-off is a regular function of position and time, and does not affect the singularity of the stress field at the fracture tip.
Let 
$x$ denote a moving coordinate centred on the tip with the 
$x$-axis pointing inside the fracture. Let 
$w(x,t)$, 
$p(x,t)$ and 
$q(x,t)$ denote the fracture aperture, net pressure and flux, all functions of position 
$x$ and time 
$t$. The problem is formulated in terms of the net pressure defined as 
$p=p_{f}-\sigma _{0}$ instead of the fluid pressure 
$p_{f}(x,t)$, recognizing that 
$\sigma _{0}$ introduces only a shift to the fluid pressure 
$p_{f}(x,t)$ when the crack is completely filled by the fracturing fluid. By convention, the flux 
$q$ is taken as positive when directed opposite to the 
$x$-axis; thus flux 
$q$ and tip velocity 
$V$ have the same sign convention. The equations governing 
$w(x,t)$, 
$p(x,t)$ and 
$q(x,t)$ depend on, besides 
$V$: Young's modulus 
$E$, Poisson's ratio 
$\nu$, and toughness 
$K_{Ic}$ of the solid; viscosity 
$\mu$ of the fluid; and also Carter's leak-off coefficient 
$C_{L}$ (as in the fracture propagating phase) or more generally on a known regular leak-off function 
$g(x,t)$. However, the equations are formulated here in terms of the alternative parameters
\begin{equation} E'=\frac{E}{1-\nu^{2}},\quad K'=4\left(\frac{2}{\rm \pi} \right)^{1/2}K_{Ic},\quad \mu'=12\mu,\quad C'=2C_{L},\end{equation}
which are introduced to keep the equations uncluttered by numerical factors, noting also that 
$E'$ is the plane strain modulus. These alternative parameters will simply be referred to as the elastic modulus (
$E'$), toughness (
$K'$), viscosity (
$\mu '$) and leak-off coefficient (
$C'$).
The elasticity integral equation for a semi-infinite crack under plane strain conditions reads (Bilby & Eshelby Reference Bilby and Eshelby1968)
\begin{equation} p=\frac{E'}{4{\rm \pi}}\int_{0}^{\infty}\frac{{\partial} w}{\partial\xi}\,\frac{\mathrm{d}\xi}{x-\xi}.\end{equation}
This equation represents asymptotically the elasticity equation in the tip region of a finite planar crack at distances from the crack front that are small compared to its radius of curvature (Peirce & Detournay Reference Peirce and Detournay2008). For the singular integral in (2.2) to converge, it is sufficient that: (i) 
$w\overset {x\rightarrow \infty }{\sim }x^{\lambda }$ with 
$\lambda \in (0,1)$; (ii) 
$\lim _{x\rightarrow 0}w=0$; and (iii) 
$w$ is a monotonically increasing function of 
$x$.
Under the approximation of lubrication theory, the viscous flow in the crack is governed by Poiseuille's law,
\begin{equation} q=\frac{w^{3}}{\mu'}\,\frac{\partial p}{\partial x},\end{equation}and by the continuity equation
\begin{equation} \frac{\partial w}{\partial t}+V\,\frac{\partial w}{\partial x}- \frac{\partial q}{\partial x}+g=0.\end{equation} According to Carter's law (Carter Reference Carter1957), the leak-off rate 
$g(x,t)$ is given by
\begin{equation} g=\frac{C'}{\sqrt{t-t_{0}(x,t)}},\end{equation}
where 
$t_{0}(x,t)$ denotes the time of first exposure to the fracturing fluid of a fixed point on the fracture wall that is located at 
$x$ at time 
$t$. The leak-off term has a square root singularity at the tip if 
$V>0$, but is finite if 
$V\le 0$. Indeed, 
$t-t_{0}(x,t)\overset {x\rightarrow 0}{\sim }x/V$ if 
$V>0$, implying that 
$g\overset {x\rightarrow 0}{\sim }C'(V/x)^{1/2}$ in that case. However, as stated earlier, the assumption of Carter leak-off is relaxed when 
$V\le 0$, with 
$g(x,t)$ simply assumed to be a known regular function.
The aperture at the fracture tip must satisfy the condition
\begin{equation} \lim_{x\rightarrow0}\frac{w(x)}{x^{1/2}}=\frac{K'}{E'}\,h(V),\end{equation}
where 
$h(V)$ is a set-valued function defined as
\begin{equation} h(V)=\begin{cases} 1, & V>0,\\ [0,1], & V=0,\\ 0, & V<0. \end{cases}\end{equation}
Equation (2.6) is equivalent to stating that: (i) the stress intensity factor 
$K_{I}$ is equal to toughness 
$K_{Ic}$ if the fracture propagates (
$V>0$) – the classical expression for the linear elastic fracture mechanics (LEFM) propagation criterion; (ii) 
$0< K_{I}< K_{Ic}$ if the fracture is at rest (
$V=0$); and (iii) 
$K_{I}=0$ if the fracture is receding (
$V<0$). In particular, the condition (2.6) for 
$V<0$ implies that the power-law index 
${{\lambda }}>1/2$ if 
$w\sim x^{\lambda }$ as 
$x\rightarrow 0$, and the fracture is closed, 
$w(x)=0$, for 
$x<0$.
3. General considerations about tip asymptotes
We are now considering asymptotic solutions for 
$w(x,t)$ of the form
\begin{equation} w(x,t)=A(t)\,x^{\lambda},\end{equation}
with the power-law index 
$\lambda$ constrained to the range
\begin{equation} \tfrac{1}{2}\le\lambda\le1.\end{equation}
The lower-bound restriction on 
$\lambda$ stems from the requirement for the elastic energy release rate at the crack tip to be finite (Rice Reference Rice1968), while the upper-bound limit results from an inability to satisfy simultaneously the elasticity and the lubrication equations if 
$\lambda >1$, as will become clear in § 5.2.
By invoking the elasticity equation (2.2) and Poiseuille's law (2.3), the asymptotic behaviour of 
$q(x,t)$, consistent with (3.1), can be derived. The asymptotics of 
$w(x,t)$ and 
$q(x,t)$ can then be used, in conjunction with the continuity equation (2.3), to identify the power-law index 
$\lambda$ corresponding to different dominant balances in the continuity equation. Different values of the index 
$\lambda$ can thus be related to different phases in the evolution of the hydraulic fracture.
The solution of the elasticity equation (2.2), for an aperture 
$w$ varying as the power law (3.1), is given by (Oberhettinger Reference Oberhettinger1970)
\begin{equation} p=AE'\,\frac{\lambda}{4}\cot({\rm \pi}\lambda)\,x^{\lambda-1}, \quad 0<\lambda<1,\end{equation}
noting that the restriction on 
$\lambda$ also defines the conditions for which the aperture (3.1) is an eigenfunction of the integral operator in (2.2). However, 
$\lambda$ is necessarily restricted to 
$\lambda \ge \frac {1}{2}$ in the context of elasticity, as 
$\lambda$ in the range 
$(0,\frac {1}{2})$ is associated with an infinite energy release rate.
We note that for the near-tip asymptotic behaviour 
$w\overset {x\rightarrow 0}{\sim }Ax$,
\begin{equation} p\overset{x\rightarrow0}{\sim}\frac{AE'}{4{\rm \pi}}\ln x.\end{equation}
This asymptotic expression for the net pressure for the case 
$\lambda =1$ can be obtained by considering the dominant term of the solution near the tip of a finite fracture (Adachi & Detournay Reference Adachi and Detournay2002; Peirce & Detournay Reference Peirce and Detournay2022b).
Differentiating Poiseuille's law (2.3) with aperture 
$w$ given by (3.1), and net pressure 
$p$ given by (3.3) if 
$1/2<\lambda <1$ or by (3.4) if 
$\lambda =1$, yields
$$\begin{gather} \frac{{\mathrm{d}}q}{{\mathrm{d}}\kern0.06em x}=\lambda(\lambda-1)\left(\lambda- \frac{1}{2}\right)\cot({\rm \pi}\lambda)\,\frac{A^{4}E'}{\mu'}\,x^{4\lambda-3}, \quad\frac{1}{2}<\lambda<1, \end{gather}$$
$$\begin{gather}\frac{{\mathrm{d}}q}{{\mathrm{d}}\kern0.06em x}=\frac{A^{4}E'}{2{\rm \pi}\mu'}\,x, \quad\lambda=1, \end{gather}$$
keeping in mind that (3.5) and (3.6) apply only asymptotically for 
$x\rightarrow 0$.
In order to determine 
${\mathrm {d}}q/{\mathrm {d}}\kern0.06em x$ in the particular case 
$\lambda =\tfrac {1}{2}$, we need to account for the next-order term in the asymptotic expansion of 
$w$, as 
$w\sim x^{1/2}$ is strictly compatible only with an inviscid fluid or a fluid at rest in the context of an hydraulic fracture after noting that (3.3) reduces to 
$p=0$ if 
$\lambda =\tfrac {1}{2}$. The next-order term depends, however, on whether the fracture is at rest or propagating, and on whether the medium is permeable or impermeable (Garagash et al. Reference Garagash, Detournay and Adachi2011). The case of a deflating fracture at rest is analysed in § 5, while the case of a hydraulic fracture propagating in an elastic medium with toughness is summarized next.
4. Tip asymptotics near the end of the propagation phase
The tip asymptotics for a hydraulic fracture propagating in a permeable elastic medium has been constructed using the device of a semi-infinite fracture moving steadily at velocity 
$V$ under the condition of plane strain (Lenoach Reference Lenoach1995; Adachi & Detournay Reference Adachi and Detournay2008; Garagash et al. Reference Garagash, Detournay and Adachi2011). This asymptotic solution has a multiscale nature characterized by two length scales, 
$\ell _{\tilde {m}k'}$ and 
$\ell _{m\tilde {m}}$:
\begin{equation} \ell_{\tilde{m}k'}=\frac{K^{\prime8}}{4E^{\prime6} C^{\prime2}\mu^{\prime2}V},\quad\ell_{m\tilde{m}}= \frac{2^{6}C^{\prime6}E^{\prime2}}{\mu^{\prime2}V^{5}}.\end{equation}
The structure of the solution depends on the number 
$\chi$ defined in terms of the length scale ratio as Garagash et al. (Reference Garagash, Detournay and Adachi2011)
\begin{equation} {\chi}={\left(\frac{\ell_{m\tilde{m}}}{\ell_{\tilde{m}k'}}\right)^{1/8}} ={\frac{2C^{\prime}E^{\prime}}{K^{\prime}V^{1/2}}}.\end{equation}
If 
$\chi$ is 
$O(100)$ or larger, then the crack aperture behaves as 
$x^{1/2}$ in the near field, 
$x^{5/8}$ at intermediate distance, and 
$x^{2/3}$ in the far field. In particular, the LEFM asymptote 
$w=(K'/E')x^{1/2}$ applies approximately to the region 
$0< x\lesssim 10^{-7}\ell _{\tilde {m}k'}$ for large 
$\chi$.
Noting that 
$\ell _{\tilde {m}k'}\sim V^{-1}$ and 
$\chi \sim V^{-1/2}$, the near-tip region of a finite hydraulic fracture is dominated by the LEFM asymptote near the end of the propagation phase after fluid injection has stopped. In this region of LEFM dominance, the pressure gradient is given by (Garagash et al. Reference Garagash, Detournay and Adachi2011)
\begin{equation} \frac{\mathrm{d}p}{\mathrm{d}\kern0.06em x}=\frac{2C'\mu'E'^{3}V^{1/2}}{K'^{3}x}, \end{equation}
implying that the flux is 
$q\sim x^{1/2}$. Thus the three dominant terms 
$V\,\partial w/\partial x$, 
$\partial q/\partial x$ and 
$g$ in the continuity equation (2.4) have the same singularity 
$x^{-1/2}$ at the fracture tip. As will be shown below, the dominant balance in the continuity equation changes during deflation of the fracture.
5. Near-field tip asymptotics during fracture arrest and recession
After the fracture stops propagating, it is in a state of arrest that lasts as long as the stress intensity factor 
$0< K< K'$. The arrest phase is then followed by recession of the tip until the fracture closes completely. In this section, we study the near-field tip asymptotics during the phases of arrest and recession, as well at the transition between arrest and recession, while relaxing the assumption of Carter's leak-off. We refer to these solutions as vertex solutions.
5.1. Arrest (
$K>0$, $V=0$)
During the arrest phase (
$V=0$), the stress intensity factor 
$K$ decreases steadily from 
$K^{\prime }$ to 
$0$. The near-tip asymptote is thus given by LEFM:
\begin{equation} w\stackrel{x\rightarrow0}{\sim}\ell_{k}^{1/2}x^{1/2},\quad \ell_{k}=\left(\frac{K}{E^{\prime}}\right)^{2},\end{equation}
with 
$\ell _{k}$ a decreasing function of time. We refer to (5.1a,b) as the 
$k$-asymptote. Once the fracture stops propagating, the leak-off 
$g(x,t)$ is no longer singular at the crack tip, and to first order, it is assumed to be spatially uniform in the asymptotic tip region. To acknowledge this approximation, leak-off is now denoted by 
$g_{0}(t)$, a regular function of time.
Considering the continuity equation (2.4), which can now be written as
\begin{equation} \frac{\partial w}{\partial t}-\frac{\partial q}{\partial x}+g_{0}=0,\end{equation}
and the aperture asymptote (5.1a,b), it is evident that the rate term 
$\partial w/\partial t$ in (5.2) is subdominant, and that the leak-off 
$g_{0}$ can be balanced only by the divergence of the flux as 
$x\rightarrow 0$. Hence integrating the dominant terms in (5.2) with the condition 
$q(0)=0$ yields
\begin{equation} q=g_{0}x,\quad x\rightarrow0.\end{equation}Further integrating Poiseuille's law, while taking into account (5.1a,b) and (5.3), leads to the non-singular pressure field in the tip region
\begin{equation} p=p_{0}+\frac{2\mu^{\prime}g_{0}}{\ell_{k}^{3/2}}\,x^{1/2}, \quad x\rightarrow0, \end{equation}
where the finite tip pressure 
$p_{o}$ and the length sale 
$\ell _{k}$ are both functions of time.
5.2. Arrest–recession transition ($K=0$, $V=0$)
At the end of the arrest phase, 
$K=0$ and 
$V=0$. Although the passage from arrest to recession is instantaneous, the transition is accompanied by a switch in the near-field asymptote, as shown next.
To construct the tip asymptote at the arrest–recession transition, we assume that 
$w(x)\sim x^{\lambda }$ as 
$x\rightarrow 0$, and again neglect the rate term 
$\partial w/\partial t$ in (5.2), since it is subdominant compared to 
$g_{0}$ as 
$x\rightarrow 0.$ Thus the continuity equation at the arrest–recession transition is again given asymptotically by (5.3). We further note that the power-law index 
$\lambda$ is necessarily in the range 
$1/2<\lambda <1$. Indeed, 
$\lambda >1/2$ since 
$K=0$; also, 
$\lambda <1$, because the flux divergence deduced from elasticity and Poiseuille's law would be subdominant to 
$g_{0}$ for 
$\lambda \ge 1$, in contradiction to (5.3).
Combining the elastic eigensolution (3.1) and (3.3), and Poiseuille's law (2.3), yields
\begin{equation} q=\lambda(\lambda-1)\cot({\rm \pi}\lambda)\,\frac{A^{4}E^{\prime}}{4 \mu^{\prime}}\,x^{4\lambda-2},\quad x\rightarrow0.\end{equation}
Then after inserting (5.3) in (5.5), identifying the power-law index 
$\lambda$ so as to remove the dependence of the equation on 
$x$, and finally solving the remaining algebraic equation for 
$A$, leads to
\begin{equation} \lambda=\tfrac{3}{4},\quad A=\beta_{g}\ell_{g}^{1/4},\end{equation}
with the coefficient 
$\beta _{g}$ and the length scale 
$\ell _{g}$ given by
\begin{equation} \beta_{g}=\left(\frac{64}{3}\right)^{1/4}\simeq2.149,\quad \ell_{g}=\frac{\mu^{\prime}g_{0}}{E^{\prime}}.\end{equation}Hence the asymptotic expressions for the aperture and the net pressure at the arrest–recession transition read
\begin{equation} w\stackrel{x\rightarrow0}{\sim}\beta_{g}\ell_{g}^{1/4}x^{3/4},\quad \frac{p}{E^{\prime}}\stackrel{x\rightarrow0}{\sim}- \frac{3\beta_{g}}{16}\left(\frac{\ell_{g}}{x}\right)^{1/4}.\end{equation}
We refer to this asymptote as the 
$g$-asymptote.
5.3. Recession ($K=0$, $V<0$)
We again search for an asymptotic expression of the form 
$w(x)\sim x^{\lambda }$ as 
$x\rightarrow 0$, where, for the reasons outlined above, the power-law index 
$\lambda$ is in the range 
$1/2<\lambda \le 1$. However, in contrast to the arrest and transition cases, the full continuity equation (2.4) needs to be considered when the fracture is receding.
It can be shown readily that the continuity equation (2.4) can be satisfied only if 
$\lambda =1$. Indeed, with 
$\lambda =1$, leak-off at the tip is balanced during recession by the advective term 
$|V|\,\partial w/\partial x$ rather than the flux divergence 
$\partial q/\partial x$ as is the case during arrest, while the two other terms are subdominant as 
$\partial w/\partial t,\partial q/\partial x\sim x$. Hence the leading-order match yields
\begin{equation} -V\,\frac{\partial w}{\partial x}=g_{0},\end{equation}while matching the next order yields
\begin{equation} \frac{\partial w}{\partial t}=\frac{\partial q}{\partial x}, \quad x\rightarrow0,\end{equation}
noting again that 
$g_{0}$ is not singular as in the arrest phase. (A power-law index 
${\lambda =2/3}$ could in principle balance 
$\partial w/\partial x$ and 
$\partial q/\partial x$, but the two terms cannot balance algebraically because of the sign mismatch.)
The dominant balance (5.9) yields a positive aperture factor 
$A=-g_{0}/V=g_{0}/|V|$, hence
\begin{equation} w=\frac{g_{0}}{|V|}\,x,\quad p=\frac{g_{0}E'}{4{\rm \pi}\,|V|}\ln x, \quad x\rightarrow0,\end{equation}
which will be referred as the 
$r$-asymptote. It will be convenient, when constructing the recession multiscale asymptote, to define the length scale 
$\ell _{r}$ as
\begin{equation} \ell_{r}=\frac{\mu^{\prime}\,|V|}{E^{\prime}}.\end{equation} Integrating (3.6) with 
$q(0)=0$ shows that 
$q>0$ in the tip region, thus implying that the fluid is flowing towards the tip, even though the crack is receding. Furthermore, we deduce from (5.10) that 
$\partial w/\partial t>0$, since 
$\partial q/\partial x>0$ according to (3.6). In other words, the asymptotic aperture at a fixed distance from the moving tip is increasing with respect to time. However, it can be shown that in a fixed coordinate system, 
$Dw/Dt=\partial w/\partial t+V\,\partial w/\partial x<0$ as 
$x\rightarrow 0$, since 
$\partial w/\partial t\sim x$ and is subdominant to 
$V\,\partial w/\partial x$, which is a negative 
$x$-independent quantity.
6. Multiscale tip asymptotics during fracture arrest and recession
6.1. The connection problem
Changes in the power-law index of the tip aperture 
$w\sim x^{\lambda }$, as the fracture evolves during the arrest and recession phases (
$\lambda =1/2$ for 
$K>0$ and 
$V=0$, 
$\lambda =3/4$ for 
$K=0$ and 
$V=0$, and 
$\lambda =1$ for 
$K=0$ and 
$V<0$), suggest the existence of multiscale asymptotes in the progressive transition between these two phases. Specifically, we envision that the region of dominance of the 
$k$-asymptote shrinks in favour of the far-field 
$g$-asymptote, as the length scale 
$\ell _{k}$ decreases with diminishing 
$K$ during arrest. At the ephemeral arrest–recession transition, the 
$g$-asymptote fully characterizes the tip region. However, this asymptote is replaced progressively in the near field by the 
$r$-asymptote as the magnitude 
$|V|$ of the receding tip velocity increases. It is therefore expected that for a finite hydraulic fracture, the 
$g$-asymptote acts as an intermediate asymptote near the arrest–recession transition.
Thus the multiscale 
$kg$-asymptote applies when the fracture is arrested, and the 
$rg$-asymptote when it is receding. Construction of the asymptotes, referred to as edge solutions, involves connecting the vertex solutions that are present in the tip boundary layer. Following the approach described by Dontsov & Peirce (Reference Dontsov and Peirce2015), this connection problem is formulated as a nonlinear non-singular integral equation for the aperture, which can be solved using simple quadratures. This integral equation is obtained as follows. First, (2.2) is inverted (provided that 
$p\overset {x\rightarrow \infty }{\sim }O(x^{-a})$ for 
$a>0$) to yield an expression for 
$w(x)$ in terms of an integral operator acting on 
$p$ (Garagash & Detournay Reference Garagash and Detournay2000). After an integration by parts, this integral equation reads
\begin{equation} w(x)=\frac{K}{E^{\prime}}\,x^{1/2}+\frac{4}{{\rm \pi} E^{\prime}} x^{1/2}\int_{0}^{\infty}s^{1/2}\,G\left(\frac{s^{1/2}}{x^{1/2}}\right) \frac{\mathrm{d}p(s)}{\mathrm{d}s}\,\mathrm{d}s.\end{equation}
Here, 
$K$ is the scaled stress intensity factor, and 
$G(t)$ is a non-singular kernel given by
\begin{equation} G(t)=\frac{1-t^{2}}{t}\ln\left|\frac{1+t}{1-t}\right|+2,\end{equation}with
\begin{equation} G(t)=4,\ t\rightarrow0,\quad \mathrm{and}\quad G(t)\sim\frac{4}{3t^{2}},\ t\rightarrow\infty. \end{equation} A nonlinear Fredholm integral equation of the second kind for 
$w(x)$ is finally deduced by replacing the pressure gradient in (6.1) by its expression from the lubrication equation. The dominant balance in the lubrication equation depends, however, on whether the fracture is at rest or receding, as shown earlier.
6.2. $kg$-edge solution
A universal description of the 
$kg$-asymptote, independent of any physical parameter, can be achieved by selecting appropriately the scales for length (
$\ell _{kg}$), aperture (
$w_{kg}$), flux (
$q_{kg}$) and pressure (
$p_{kg}$). This is done by defining length scale 
$\ell _{kg}$ as the distance from the fracture tip at which the 
$k$- and 
$g$-asymptotes yield approximately the same aperture 
$w_{kg}$; thus 
$w_{kg}\sim \ell _{k}^{1/2}\ell _{kg}^{1/2}\sim \ell _{g}^{1/4}\ell _{kg}^{3/4}$. In view of (5.1a,b) and (5.8a,b), both scales 
$\ell _{kg}$ and 
$w_{kg}$ can be expressed in terms of 
$\ell _{k}$ and 
$\ell _{g}$ according to
\begin{equation} \ell_{kg}=\frac{\ell_{k}^{2}}{\ell_{g}},\quad w_{kg}=\frac{\ell_{k}^{3/2}}{\ell_{g}^{1/2}}.\end{equation}
From Poiseuille's law (2.3) and the continuity equation (5.3), we further deduce the scales 
$q_{kg}$ and 
$p_{kg}$:
\begin{equation} q_{kg}=g_{0}\ell_{kg},\quad p_{kg}=E'\,\frac{w_{kg}}{\ell_{kg}}.\end{equation}
After introducing the dimensionless variables 
$\hat {x}=x/\ell _{kg}$, 
$\hat {w}=w/w_{kg}$, 
$\hat {p}=p/p_{kg}$, 
${\hat{q}=q/q_{kg}}$, and accounting for 
$V=0$, the lubrication equation (2.3) and (5.3) combine to give
\begin{equation} \frac{\mathrm{d}\hat{p}}{\mathrm{d}\hat{x}}= \frac{\hat{x}}{\hat{w}^{3}}.\end{equation}Scaling the elastic integral equation (6.1) and combining it with (6.6) yields
\begin{equation} \hat{w}(\hat{x})=\hat{x}^{1/2}\left[1+\frac{4}{\rm \pi} \int_{0}^{\infty}G\left(\frac{\hat{s}^{1/2}}{\hat{x}^{1/2}} \right)\frac{\hat{s}^{3/2}}{\hat{w}(\hat{s})^{3}}\, \mathrm{d}\hat{s}\right],\end{equation}
noting also that 
$\hat {w}=\hat {x}^{1/2}$ if 
$\hat {x}\ll 1$, and 
$\hat {w}=\beta _{g}\hat {x}^{3/4}$ if 
$\hat {x}\gg 1$. The universal 
$kg$-asymptote 
$\hat {w}({{\hat {x}}})$ is the solution of the Fredholm integral equation (6.7).
To solve for 
$\hat {w}(\hat {x})$, the integral equation (6.7) is reformulated as (Dontsov & Peirce Reference Dontsov and Peirce2015)
\begin{equation} \hat{\omega}(\hat{\xi})=1+\frac{8}{\rm \pi}\int_{0}^{\infty}G \left(\frac{\hat{\eta}}{\hat{\xi}}\right)\frac{\hat{\eta}\, \mathrm{d}\hat{\eta}}{\hat{\omega}(\hat{\eta})^{3}},\end{equation}
where the variables 
$\hat {\omega }$, 
$\hat {\xi }$ and 
$\hat {\eta }$ are defined as
\begin{equation} \hat{\omega}=\frac{\hat{w}}{\hat{x}^{1/2}},\quad \hat{\xi}=\hat{x}^{1/2},\quad \hat{\eta} =\hat{s}^{1/2}.\end{equation}
Under this transformation, the 
$k$- and 
$g$-asymptotes transform to 
$\hat {\omega }(0)=1$ and 
$\hat {\omega }=\beta _{g}\hat {\xi }^{1/2}$ as 
$\hat {\xi }\rightarrow \infty$, respectively. These asymptotic behaviours can actually be recovered directly from the transformed integral equation (6.8) by assessing the integral in the limits 
$\hat {\xi }=0$ and 
$\hat {\xi }\rightarrow \infty$, and taking into account the asymptotic behaviours (6.3a,b) of the function 
$G(t)$, and the result (Dontsov & Peirce Reference Dontsov and Peirce2015)
\begin{equation} \int_{0}^{\infty}\frac{G(t)}{t^{\gamma}}\,\mathrm{d}t= \frac{2{\rm \pi}}{\gamma(2-\gamma)}\tan\left(\frac{\rm \pi}{2}\gamma \right).\end{equation} Since the integrand in (6.8) is positive and non-singular, a numerical solution of 
$\hat {\omega }(\hat {\xi })$ can be obtained by solving a system of nonlinear algebraic equations formulated by discretizing the integral using the trapezoidal rule. To capture correctly the complete 
$kg$-asymptote, the grid points should be spaced uniformly on a logarithmic scale.
As in Dontsov & Peirce (Reference Dontsov and Peirce2015), it is possible to obtain an approximate 
$kg$-edge solution, which in this case has relative error less than 
$3\,\%$, by differentiating (6.8) and assuming a power-law behaviour for 
$\hat {\omega }$ to obtain a separable ordinary differential equation, whose solution, along with the condition 
$\hat {\omega }(0)=1$, yields
\begin{equation} \hat{\omega}\approx(1+\beta_{g}^{4}\hat{\xi}^{2})^{1/4}\quad \text{or}\quad\hat{w}\approx\hat{x}^{1/2}(1+\beta_{g}^{4} \hat{x})^{1/4}.\end{equation} In figure 2, we plot 
$\hat {x}^{1/2}/\hat {w}$ versus 
$\hat {x}$ (or equivalently 
$1/\hat {\omega }$ versus 
$\hat {\xi }^{2}$). We have chosen to plot the reciprocal of 
$\hat {\omega }$ as this emphasizes the variation in 
$\hat {\omega }$, with respect to the scaled variables, between the small- and large-
$\hat {\xi }$ asymptotic behaviours. The solid curve in this figure represents the numerical solution of (6.8), and the dashed curve the approximate solution (6.11).
Figure 2. The 
$kg$-asymptote plotted as 
$\hat {x}^{1/2}/\hat {w}$ versus 
$\hat {x}$ (or equivalently 
$1/\hat {\omega }$ versus 
$\hat {\xi }^{2}$): numerical solution (continuous line) and approximate closed-form solution (dashed line).
6.3. $rg$-edge solution
For the multiscale tip asymptote applicable to the recession phase, we proceed in a manner similar to the construction of the 
$kg$-transition. Now the 
$r$-asymptote (instead of the 
$k$-asymptote) dominates the near-tip region, 
$x\ll \ell _{rg}$, and the 
$g$-asymptote applies in the far-tip region, 
$x\gg \ell _{rg}$, where 
$\ell _{rg}$ is the transition length scale of the 
$rg$-asymptote.
The scales 
$\ell _{rg}$ and 
$w_{rg}$ are deduced from the 
$r$- and 
$g$-asymptotes by determining the distance from the tip at which both asymptotes yield approximately the same aperture:
\begin{equation} \ell_{rg}=\frac{\ell_{r}^{4}}{\ell_{g}^{3}},\quad w_{rg}=\frac{\ell_{r}^{3}}{\ell_{g}^{2}}. \end{equation}
Hence 
$\tilde {w}=\tilde {x}$ if 
$\tilde {x}\ll 1$, and 
$\tilde {w}=\beta _{g}\tilde {x}^{3/4}$ if 
$\tilde {x}\gg 1$, with 
$\tilde {x}=x/\ell _{rg}$ and 
$\tilde {w}=w/w_{rg}$. Moreover, from the continuity equation (2.4) and Poiseuille's law (2.3), we deduce the flux scale 
$q_{rg}$ and the pressure scale 
$p_{rg}$:
\begin{equation} q_{rg}=|V|\,w_{rg},\quad p_{rg}=E'\,\frac{w_{rg}}{\ell_{rg}}. \end{equation} In the early stage of the recession, when the tip is under the 
$rg$-asymptotic umbrella, we can again neglect the rate term 
$\partial w/\partial t$ in the continuity equation (2.4), which, after scaling and integration and noting that 
$V<0$ in (2.4), now reads
\begin{equation} \tilde{q}=\tilde{x}-\tilde{w}.\end{equation}Hence the lubrication equation simplifies to
\begin{equation} \frac{\mathrm{d}\tilde{p}}{\mathrm{d}\tilde{x}}= \frac{\tilde{x}-\tilde{w}}{\tilde{w}^{3}},\end{equation}
where the tilde denotes a dimensionless variable in the 
$rg$-scaling.
For the 
$rg$-transition, the elasticity equation (6.1) becomes
\begin{equation} \tilde{w}(\tilde{x})=\frac{4\tilde{x}^{1/2}}{\rm \pi} \int_{0}^{\infty}\tilde{s}^{1/2}\,G \left(\frac{\tilde{s}^{1/2}}{\tilde{x}^{1/2}}\right) \frac{\tilde{s}-\tilde{w}}{\tilde{w}^{3}}\,\mathrm{d}\tilde{s},\end{equation}
after dropping the inhomogeneous term 
$\tilde {x}^{1/2}$ since 
$K=0$, and replacing the pressure gradient by its expression derived from the lubrication equation (6.15). We note, however, that 
$\tilde {w}=\tilde {s}$ is in the null space of the integral operator (6.16). Moreover, 
$\tilde {w}\sim \tilde {s}$ is the near-tip asymptote valid for 
$\tilde {s}\ll 1$. We therefore define the function 
$\tilde {\omega }(\tilde {x})$ as a perturbation of the near-tip asymptote, i.e.
\begin{equation} \tilde{\omega}(\tilde{x})=\frac{\tilde{w}(\tilde{x})}{\tilde{x}}-1,\end{equation}
such that 
$\tilde {\omega }(0)=0$ and 
$\tilde {\omega }(\infty )=-1$
The integral equation can then be rewritten as
\begin{equation} \tilde{\omega}(\tilde{x})={-}1-\frac{4}{{\rm \pi}\tilde{x}^{1/2}} \int_{0}^{\infty}G\left(\frac{\tilde{s}^{1/2}}{\tilde{x}^{1/2}}\right) \frac{\tilde{\omega}(\tilde{s})}{\tilde{s}^{3/2}(1+ \tilde{\omega}(s))^{3}}\,\mathrm{d}\tilde{s}.\end{equation}
In view of the limiting behaviours (6.3a,b) of the function 
$G(t)$, the above integral converges if 
$\tilde {\omega }(\tilde {x})\sim \tilde {x}^{\gamma }$ as 
$\tilde {x}\rightarrow 0$, provided that 
$\gamma >\text {\ensuremath {1/2}}$.
Figure 3 shows 
$\tilde {w}(\tilde {x})/\tilde {x}$ as a function of the scaled distance to the fracture tip, 
$\tilde {x}$. We have chosen to plot the shifted perturbation 
$1+\tilde {\omega }$ as it varies from 
$0$ to 
$1$, noting that the perturbation 
$\tilde {\omega }$ is bounded above by the asymptote 
$\tilde {\omega }\overset {\tilde {x}\rightarrow 0}{\rightarrow }0$ associated with the 
$r$-vertex solution, and bounded below by the asymptote 
$\tilde {\omega }\overset {\tilde {x}\rightarrow \infty }{\rightarrow }-1+\beta _{g}\tilde {x}^{-1/4}$ associated with the 
$g$-vertex solution. The solid black curve in figure 3 represents the numerical solution of (6.18).
Figure 3. The 
$rg$-asymptote plotted as 
$\tilde {w}(\tilde {x})/\tilde {x}$ versus 
$\tilde {x}$.
6.4. Application of the $kg$- and $rg$-asymptotes during deflation
Here, we outline briefly the determination of the stress intensity factor 
$K$ during the arrest phase of a deflating fracture, using the 
$kg$-asymptote within the framework of a numerical hydraulic fracturing simulator. This methodology is inspired by procedures developed for implementing multiscale tip asymptotics in numerical codes to simulate propagating hydraulic fractures (Peirce Reference Peirce2015, Reference Peirce2016; Dontsov & Peirce Reference Dontsov and Peirce2017).
The methodology relies on the ability to compute the fracture aperture at a grid point, away from the tip but still inside the asymptotic region, by solving numerically the system of equations governing the response of a hydraulic fracture during deflation. Assume that at a certain time 
$t$, the aperture 
$w_{n}^{(k)}$ at node 
$n$ located at distance 
$\ell _{n}$ from the tip has been calculated iteratively, with superscript 
$(k)$ denoting the current iteration count at time 
$t$. The pair (
$\ell _{n},w_{n}^{(k)}$) is forced to be mapped onto the 
$kg$-asymptotic solution 
$\hat {w}(\hat {x})$ by selecting the appropriate stress intensity factor 
$K$. However, this new value of 
$K$ impacts the asymptotic aperture of the fracture behind node 
$n$, which in turn affects the aperture at node 
$n$ through the elasticity and the lubrication equation. An iterative procedure is thus needed to determine the arrest solution at a given time 
$t$ to correctly identify 
$K$. It is important to point out that the distance 
$\ell _{n}$ should be constrained by 
$\ell _{n}\lesssim 10^{6}\ell _{kg}$ so that the node is outside the region of dominance of the 
$g$-asymptote, as all information about 
$K$ would otherwise be lost since
\begin{equation} w\overset{x\rightarrow\infty}{\sim}w_{kg}\beta_{g} \left(\frac{x}{\ell_{kg}}\right)^{3/4}= \beta_{g}\ell_{g}^{1/4}x^{3/4}. \end{equation}
A similar approach is used to determine the recession velocity 
$V$ using the 
$rg$-asymptote. Again, the nodal point must not be inside the 
$g$-asymptotic region, i.e. 
$\ell _{n}\lesssim 10^{9}\ell _{rg}$, noting that
\begin{equation} w\overset{x\rightarrow\infty}{\sim}w_{rg}\beta_{g} \left(\frac{x}{\ell_{rg}}\right)^{3/4}=\beta_{g}\ell_{g}^{1/4}x^{3/4}, \end{equation}
which shows that the asymptote is agnostic about the tip velocity when 
$x\gg \ell _{rg.}$ The 
$rg$-edge solution is used until the point at which there is a negligible difference between the value of 
$|V|$ determined from the 
$rg$-edge solution and that given by the linear asymptote in (5.11a,b).
The detailed procedure for applying the 
$kg$- and 
$rg$-asymptotes to the numerical modelling of a deflating fracture is described elsewhere (Peirce Reference Peirce2022; Peirce & Detournay Reference Peirce and Detournay2022b).
7. Concluding remarks
This paper describes the construction of two multiscale tip asymptotes for a hydraulic fracture deflating in a permeable elastic medium, the 
$kg$-asymptote when the fracture is at rest, and the 
$rg$-asymptote when the fracture is receding. The asymptotes were obtained by solving a Fredholm integral equation of the second kind, formulated in terms of the aperture for a semi-infinite deflating fracture that is either at rest or steadily receding. The arrest 
$kg$-asymptote is characterized in the near field by the classic LEFM asymptote 
$w\sim x^{1/2}$ as 
$x\rightarrow 0$, while the receding asymptote behaves as 
$w\sim x$ as 
$x\rightarrow 0$; however, both asymptotes share the same power law 
$w\sim x^{3/4}$ as 
$x\rightarrow \infty$. Thus the fluid pressure is regular when the fracture is at rest, but has a logarithmic singularity during recession.
The scaled tip asymptotes are universal since they do not depend on any parameter. Scaling indicates that: during arrest, the region of dominance of the 
$1/2$ asymptote shrinks to the benefit of the intermediate 
$3/4$ asymptote as the fracture deflates; and during recession, a linear 
$1/1$ asymptote develops progressively at the fracture tip with increasing receding velocity, with the 
$3/4$ becoming again an intermediate asymptote. Hence only the fleeting 
$3/4$ asymptote remains at the arrest–recession transition point. It is worth noting that the multiscale receding asymptote has an unusual structure in that the power-law index is larger in the near field than in the far field. This ordering is dictated by the nature of the 
$3/4$ asymptote, which cannot exist with a non-zero velocity and is thus agnostic about the velocity, hence is unable to balance the leak-off as 
$x\rightarrow 0$ during recession. Finally, note that the asymptotes for a deflating fracture can be extended to cases where the criterion for fracture closure is more generally described by 
$w=w_0$. Here, 
$w_0$ is a residual aperture associated, for example, with the presence of proppant in the fracture. The tip asymptotes then apply to the difference aperture field 
$w-w_0$.
These universal multiscale asymptotes are key to determining the decaying stress intensity factor during arrest, the time at which the fracture transitions from arrest to recession, and the negative front velocity during recession when simulating the deflation of a hydraulic fracture in a permeable elastic medium. The dependence of the tip asymptotic response on time is thus only indirect, via the stress intensity factor if the fracture is arrested, or via the tip velocity if receding. It further requires combining consideration of the finite fracture and of the tip asymptotes.
The arrest and recession asymptotes are instrumental both for implementing robust algorithms for simulating deflating fractures (Peirce Reference Peirce2022; Peirce & Detournay Reference Peirce and Detournay2022a) and for constructing closed-form solutions for radial and plane strain fractures in the latest stage of closure (Peirce & Detournay Reference Peirce and Detournay2022b). Such ‘sunset’ solutions can be used to interpret the leak-off coefficient or the in situ stress from measurements collected during shut-in.
It has been assumed in this work that the permeable solid has toughness 
$K' > 0$. Consideration of the case 
$K'=0$ would require analysing the evolution of the asymptotics during the direct transition from propagation to recession, as there is no arrest phase in this particular case. The case 
$K'>0$ for an impermeable solid is treated in Appendix A, where it is shown that a deflating hydraulic fracture in an impermeable medium cannot recede even if it is bleeding fluid back to the borehole.
Funding
A.P. was supported by the Natural Sciences and Engineering Research Council of Canada (NSERC) (grant no. RGPIN-2015-06039) and the British Columbia Oil and Gas Commission. E.D. gratefully acknowledges support provided by the T.W. Bennett Chair in Mining Engineering and Rock Mechanics.
Declaration of interests
The authors report no conflict of interest.
Appendix A. Fracture closure in an impermeable medium
In an impermeable medium, the deflation of a hydraulic fracture following shut-in is associated with indefinite propagation if 
$K'=0$, and propagation followed by arrest if 
$K'>0$. Indeed, the volume of fluid trapped in the fracture is constant after shut-in, therefore the fracture deflates as it propagates with the pressure progressively dropping. If 
$K'>0$, then the fracture will come to rest after a finite time, when the pressure becomes uniform and the fracture stays open indefinitely. If 
$K'=0$, then a state of uniform pressure can be achieved only when the net pressure vanishes, i.e. after an infinite time. In this appendix, we establish these results using an asymptotic analysis of the lubrication equation in the tip region. This analysis assumes that there is no lag between the fluid front and the fracture tip.
The case of flow-back is more complicated than shut-in as the fracture inlet at the borehole wall could close and open cyclically. Although an analysis of the fracture response during flow-back is beyond the scope of this paper, we prove nonetheless that the tip of a hydraulic fracture in an impermeable medium cannot recede during flow-back. If 
$K'=0$, then the fracture can propagate only until it closes. If 
$K'>0$, then the fracture can either arrest or propagate. These conclusions are based essentially on an analysis of the continuity equation in the vicinity of the tip,
\begin{equation} \frac{\partial w}{\partial t}+V\,\frac{\partial w}{\partial x}- \frac{\partial q}{\partial x}=0,\end{equation}
taking into account the tip asymptotic behaviour of the fields 
$w(x,t)$ and 
$q(x,t)$ that are derived from the elasticity and lubrication theories established in § 3.
The impossibility of a hydraulic fracture receding in an impermeable medium is known as the Stevenson condition in the dyke literature. However, the argument put forward by Stevenson (Reference Stevenson1982) (see also Roper & Lister Reference Roper and Lister2007) relies on the infinite amount of work needed to squeeze a viscous fluid between two approaching parallel plates, and not on the impossibility of satisfying the continuity equation in the neighbourhood of the tip as presented below.
A.1. Zero toughness case
First, consider the particular case 
$K'=0$ for which the power-law exponent 
$\lambda$ of the aperture 
$w(x,t)$ is necessarily in the range 
$1/2<\lambda \le 1$ since the energy release rate is zero. In view of the dependence of each term on 
$x$ summarized in § 3, there are only two cases, 
$\lambda =1$ and 
$\lambda =2/3$, for which two of the terms in (A1) have the same power-law exponents and could, in principle, balance. It can be proven readily that 
$\lambda =2/3$ for a propagating fracture (
$V>0$) (Spence & Sharp Reference Spence and Sharp1985; Lister Reference Lister1990; Desroches et al. Reference Desroches, Detournay, Lenoach, Papanastasiou, Pearson, Thiercelin and Cheng1994). In this case, the terms 
$V\,\partial w/\partial x$ and 
$\partial q/\partial x$ balance, and the continuity equation is satisfied in the limit 
$x\rightarrow 0$ since it is dominated by these two singular terms. Hence 
$\lambda =1$ could apply, in principle, only to a deflating fracture at rest (
$V=0$) or receding (
$V<0$). However, neither case is possible as proven next. Indeed, (A1) cannot be satisfied near 
$x=0$ if 
$V<0$ and 
$w=A(t)\,x$, as there is a residual term 
$V\,A(t)$. Furthermore, a power-law index 
$\lambda =1$ implies that 
$p\sim A\ln x$ from elasticity, thus 
$q\sim A^{4}x^{2}$ according to Poiseuille's law. It follows that 
$\partial q/\partial x>0$, and satisfying the continuity equation (A1) for 
$V=0$ would then require 
$\partial w/\partial t>0$ (
$\mathrm {d}A/\mathrm {d}t>0$), which is not physically possible if the fracture is deflating. Furthermore, the negative pressure near 
$x=0$ (
$A>0$) and positive flux are also physically incompatible with a deflating fracture in an impermeable medium.
We conclude therefore if 
$K'=0$ and 
${C'=0}$ that the fracture can only propagate and thin.
A.2. Finite toughness case
Next, we consider the fracture response for 
$K'>0$ after the injection phase. First, the fracture tip slows down progressively to eventually arrest during shut-in and flow-back. The fracture then deflates if there is flow-back but without the tip receding. Indeed, following the same line of argument used for 
$K'=0$, it can be concluded that the fracture cannot recede, as a the continuity equation (A1) cannot be satisfied with 
$V < 0$. This establishes the Stevenson condition using an asymptotic analysis of the lubrication equation.
It is well understood that a multiscale asymptote characterized by a local length scale
\begin{equation} \ell_{mk'}=\frac{K'^{6}}{E'^{4}\mu'^{2}V^{2}}\end{equation}
controls the solution during propagation (Garagash & Detournay Reference Garagash and Detournay2000). If 
$\ell _{mk'}$ is small compared to the characteristic dimension of the hydraulic fracture, then the tip behaviour is dominated, at the scale of the fracture, by the viscosity asymptote 
$w\sim x^{2/3}$. In the opposite case, the tip is dominated by the toughness asymptote 
$w\sim x^{1/2}$. However, as we are concerned here about the tip response during shut-in or flow-back when the propagation velocity slows down progressively before the fracture is arrested, we focus on the toughness asymptote, noting that 
$\ell _{mk'}\sim V^{-2}$.
During the propagation phase following shut-in or flow-back, the two balanced terms 
$V\,\partial w/\partial x$ and 
$\partial q/\partial x$ in the continuity equation (A1) become dominated by the square root singularity 
$x^{-1/2}$ once the tip velocity is sufficiently small. Then invoking Poiseuille's law after recognizing that 
$q=Vw$ in the vicinity of the tip (which is deduced by integrating (A1) and taking into account 
$q(0,t)=w(0,t)=0$) yields
\begin{equation} p\overset{x\rightarrow0}{\sim}\frac{\mu'VE'^{2}}{K'^{2}}\ln x.\end{equation}Since the strength of the pressure logarithmic singularity is proportional to the tip velocity, the fluid pressure becomes regular at the tip when the fracture stops propagating.
During deflation of the hydraulic fracture when the fracture is at rest (
$V=0$), the aperture is given asymptotically by
\begin{equation} \hat{w}\simeq\frac{K(t)}{E'}\,\hat{x}^{1/2},\end{equation}
according to LEFM, with 
$K\le K'$ denoting the (reduced) mode I stress intensity factor 
$K=4\sqrt {2/{\rm \pi} }K_{I}$. As the fracture is deflating, we expect that 
$\dot {K}={\mathrm {d}}K/{\mathrm {d}}t<0$ and the continuity equation (A1) reduces to
\begin{equation} \frac{\partial q}{\partial x}=\frac{\dot{K}}{E'}\,x^{1/2}.\end{equation}
Since 
$q=0$ at 
$x=0$,
\begin{equation} q=\frac{2\dot{K}}{3E'}\,x^{3/2},\end{equation}
which shows that 
$q$ is negative, i.e. the fluid is flowing away from the tip. Then, after invoking Poiseuille's law, we obtain
\begin{equation} p=\frac{2\mu'E'^{2}\dot{K}}{3K^{3}}\,x+p_{0}(t),\end{equation}
where the pressure at the tip, 
$p_{0}(t)$, is expected to be positive. Thus the pressure decreases away from the tip during deflation of a fracture at rest.
Open access
