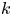 $k$-type behaviour of roughness when in-plane wavelength approaches the boundary layer thickness
$k$-type behaviour of roughness when in-plane wavelength approaches the boundary layer thicknessPublished online by Cambridge University Press: 22 January 2021
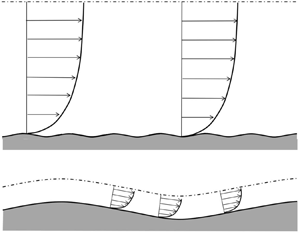
A surface roughness from a recently cleaned and painted ship's hull was scanned, scaled and replicated for laboratory testing to systematically investigate the influence of the ratio of in-plane roughness wavelength,  $\lambda$, with respect to the boundary layer thickness
$\lambda$, with respect to the boundary layer thickness  $\delta$. The experiments were performed by geometrically scaling the surface which maintains a constant effective slope
$\delta$. The experiments were performed by geometrically scaling the surface which maintains a constant effective slope  $ES_x$ and solidity
$ES_x$ and solidity  $\varLambda$, while the ratio of
$\varLambda$, while the ratio of  $\lambda /\delta$ is varied. Here we scale the scanned roughness topography by a factor of 2.5 and 15, and measure the mean velocity profiles in the turbulent boundary layers developing over these surfaces at a range of free stream velocities and streamwise measurement locations. The results show that the
$\lambda /\delta$ is varied. Here we scale the scanned roughness topography by a factor of 2.5 and 15, and measure the mean velocity profiles in the turbulent boundary layers developing over these surfaces at a range of free stream velocities and streamwise measurement locations. The results show that the  $2.5\times$ scaled roughness, which has
$2.5\times$ scaled roughness, which has  $\lambda /\delta \ll 1$, behaves in the expected
$\lambda /\delta \ll 1$, behaves in the expected  $k$-type manner, with a roughness function
$k$-type manner, with a roughness function  ${\rm \Delta} U^+$ that is proportional to the viscous-scaled roughness height. The
${\rm \Delta} U^+$ that is proportional to the viscous-scaled roughness height. The  $15\times$ surface, however, which has
$15\times$ surface, however, which has  $\lambda /\delta \approx 1$, exhibits very different non-
$\lambda /\delta \approx 1$, exhibits very different non- $k$-type behaviour. This larger surface does not approach the fully rough asymptote and also exhibits a drag penalty that is comparable to the
$k$-type behaviour. This larger surface does not approach the fully rough asymptote and also exhibits a drag penalty that is comparable to the  $2.5\times$ case despite the sixfold increase in the roughness height. Measurements on a spanwise–wall-normal plane reveal that the
$2.5\times$ case despite the sixfold increase in the roughness height. Measurements on a spanwise–wall-normal plane reveal that the  $15\times$ surface has introduced a large-scale spanwise variation in mean streamwise velocity (dispersive stresses) that extend far beyond the logarithmic region. Together this evidence suggests that a demarcation between
$15\times$ surface has introduced a large-scale spanwise variation in mean streamwise velocity (dispersive stresses) that extend far beyond the logarithmic region. Together this evidence suggests that a demarcation between  $k$-type and non-
$k$-type and non- $k$-type behaviour can occur in situations where the in-plane roughness wavelength approaches the boundary layer thickness. This finding has important implications to how we scale small-scale roughness from high Reynolds number (Re) large-scale applications for testing in low Re small-scale laboratory facilities or simulations.
$k$-type behaviour can occur in situations where the in-plane roughness wavelength approaches the boundary layer thickness. This finding has important implications to how we scale small-scale roughness from high Reynolds number (Re) large-scale applications for testing in low Re small-scale laboratory facilities or simulations.