Article contents
Nonlinear evolution of linear optimal perturbations of strongly stratified shear layers
Published online by Cambridge University Press: 20 July 2017
Abstract
The Miles–Howard theorem states that a necessary condition for normal-mode instability in parallel, inviscid, steady stratified shear flows is that the minimum gradient Richardson number, 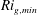 $Ri_{g,min}$ , is less than
$Ri_{g,min}$ , is less than 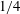 $1/4$ somewhere in the flow. However, the non-normality of the Navier–Stokes and buoyancy equations may allow for substantial perturbation energy growth at finite times. We calculate numerically the linear optimal perturbations which maximize the perturbation energy gain for a stably stratified shear layer consisting of a hyperbolic tangent velocity distribution with characteristic velocity
$1/4$ somewhere in the flow. However, the non-normality of the Navier–Stokes and buoyancy equations may allow for substantial perturbation energy growth at finite times. We calculate numerically the linear optimal perturbations which maximize the perturbation energy gain for a stably stratified shear layer consisting of a hyperbolic tangent velocity distribution with characteristic velocity  $U_{0}^{\ast }$ and a uniform stratification with constant buoyancy frequency
$U_{0}^{\ast }$ and a uniform stratification with constant buoyancy frequency 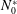 $N_{0}^{\ast }$ . We vary the bulk Richardson number
$N_{0}^{\ast }$ . We vary the bulk Richardson number 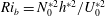 $Ri_{b}=N_{0}^{\ast 2}h^{\ast 2}/U_{0}^{\ast 2}$ (corresponding to
$Ri_{b}=N_{0}^{\ast 2}h^{\ast 2}/U_{0}^{\ast 2}$ (corresponding to 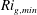 $Ri_{g,min}$ ) between 0.20 and 0.50 and the Reynolds numbers
$Ri_{g,min}$ ) between 0.20 and 0.50 and the Reynolds numbers 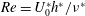 $\mathit{Re}=U_{0}^{\ast }h^{\ast }/\unicode[STIX]{x1D708}^{\ast }$ between 1000 and 8000, with the Prandtl number held fixed at
$\mathit{Re}=U_{0}^{\ast }h^{\ast }/\unicode[STIX]{x1D708}^{\ast }$ between 1000 and 8000, with the Prandtl number held fixed at 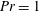 $\mathit{Pr}=1$ . We find the transient growth of non-normal perturbations may be sufficient to trigger strongly nonlinear effects and breakdown into small-scale structures, thereby leading to enhanced dissipation and non-trivial modification of the background flow even in flows where
$\mathit{Pr}=1$ . We find the transient growth of non-normal perturbations may be sufficient to trigger strongly nonlinear effects and breakdown into small-scale structures, thereby leading to enhanced dissipation and non-trivial modification of the background flow even in flows where 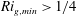 $Ri_{g,min}>1/4$ . We show that the effects of nonlinearity are more significant for flows with higher
$Ri_{g,min}>1/4$ . We show that the effects of nonlinearity are more significant for flows with higher 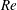 $\mathit{Re}$ , lower
$\mathit{Re}$ , lower 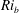 $Ri_{b}$ and higher initial perturbation amplitude
$Ri_{b}$ and higher initial perturbation amplitude 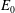 $E_{0}$ . Enhanced kinetic energy dissipation is observed for higher-
$E_{0}$ . Enhanced kinetic energy dissipation is observed for higher- 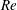 $Re$ and lower-
$Re$ and lower- 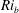 $Ri_{b}$ flows, and the mixing efficiency, quantified here by
$Ri_{b}$ flows, and the mixing efficiency, quantified here by 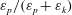 $\unicode[STIX]{x1D700}_{p}/(\unicode[STIX]{x1D700}_{p}+\unicode[STIX]{x1D700}_{k})$ where
$\unicode[STIX]{x1D700}_{p}/(\unicode[STIX]{x1D700}_{p}+\unicode[STIX]{x1D700}_{k})$ where 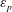 $\unicode[STIX]{x1D700}_{p}$ is the dissipation rate of density variance and
$\unicode[STIX]{x1D700}_{p}$ is the dissipation rate of density variance and 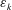 $\unicode[STIX]{x1D700}_{k}$ is the dissipation rate of kinetic energy, is found to be approximately 0.35 for the most strongly nonlinear cases.
$\unicode[STIX]{x1D700}_{k}$ is the dissipation rate of kinetic energy, is found to be approximately 0.35 for the most strongly nonlinear cases.
Information
- Type
- Papers
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 15
- Cited by


