No CrossRef data available.
Article contents
Nonlinear interaction of wind-driven oblique surface waves and parametric growth of lower frequency modes
Published online by Cambridge University Press: 12 July 2012
Abstract
Nonlinear interactions between free-surface waves of the same wave speed and wind are studied by extending the linear resonant theory of Miles (J. Fluid Mech., vol. 3, 1957, pp. 185–204). A nonlinear interaction can occur when the steepness of a primary three-dimensional wave, which propagates obliquely to the wind direction, becomes of the order of the cube of the density ratio of air to water. If a secondary wave of smaller amplitude is also an oblique wave, the nonlinear critical-layer interaction between the primary and secondary fluctuations in air generates a difference mode whose wavenumbers are equal to the differences between the primary and secondary values. In addition, the nonlinear interaction in the critical layer between the primary and difference modes induces a parametric-growth effect on the secondary surface wave, if the frequency of the primary wave is higher than that of the secondary wave. The primary wave remains linear during this ‘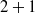 mode critical-layer interaction’ stage between two free-surface waves and a nonlinearly generated mode. The evolution of the secondary-wave amplitude is governed by an integro-differential equation and that of the difference mode is determined by an integral equation. Both inviscid and viscous numerical results show that the nonlinear growth rates become much larger than the linear growth rates. Effect of viscosity is shown to delay the onset of the nonlinear growth. The growth of the secondary and difference modes is more effectively enhanced when the signs of propagation angles of the primary and secondary waves are opposite than when they are equal. The
mode critical-layer interaction’ stage between two free-surface waves and a nonlinearly generated mode. The evolution of the secondary-wave amplitude is governed by an integro-differential equation and that of the difference mode is determined by an integral equation. Both inviscid and viscous numerical results show that the nonlinear growth rates become much larger than the linear growth rates. Effect of viscosity is shown to delay the onset of the nonlinear growth. The growth of the secondary and difference modes is more effectively enhanced when the signs of propagation angles of the primary and secondary waves are opposite than when they are equal. The 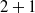 mode interaction can occur when wave steepnesses are very small. The nonlinear interaction is entirely confined to a thin critical layer, and the perturbations outside the critical layer are governed by linear equations. It is shown that the initial nonlinear growth of a free-surface wave could be governed by a mode–mode interaction in air.
mode interaction can occur when wave steepnesses are very small. The nonlinear interaction is entirely confined to a thin critical layer, and the perturbations outside the critical layer are governed by linear equations. It is shown that the initial nonlinear growth of a free-surface wave could be governed by a mode–mode interaction in air.
JFM classification
Information
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2012

