Hostname: page-component-8448b6f56d-mp689 Total loading time: 0 Render date: 2024-04-25T05:02:14.570Z Has data issue: false hasContentIssue false
  • English
  • Français

Nonlinear spectral model for rotating sheared turbulence

Published online by Cambridge University Press:  06 March 2019

Ying Zhu ,
C. Cambon ,
F. S. Godeferd Open the ORCID record for F. S. Godeferd [Opens in a new window]  and
A. Salhi
Ying Zhu*
Affiliation:
Laboratoire de Mécanique des Fluides et d’Acoustique, UMR 5509, Université de Lyon, CNRS, École Centrale de Lyon, Université Claude Bernard Lyon 1, INSA Lyon, France
C. Cambon
Affiliation:
Laboratoire de Mécanique des Fluides et d’Acoustique, UMR 5509, Université de Lyon, CNRS, École Centrale de Lyon, Université Claude Bernard Lyon 1, INSA Lyon, France
F. S. Godeferd
Affiliation:
Laboratoire de Mécanique des Fluides et d’Acoustique, UMR 5509, Université de Lyon, CNRS, École Centrale de Lyon, Université Claude Bernard Lyon 1, INSA Lyon, France
A. Salhi
Affiliation:
Laboratoire de Mécanique des Fluides et d’Acoustique, UMR 5509, Université de Lyon, CNRS, École Centrale de Lyon, Université Claude Bernard Lyon 1, INSA Lyon, France Département de Physique, Faculté des Sciences de Tunis, 1060, Tunis, Tunisia
*
†Email address for correspondence: ying.zhu@doctorant.ec-lyon.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

We propose a statistical model for homogeneous turbulence undergoing distortions, which improves and extends the MCS model by Mons, Cambon & Sagaut (J. Fluid Mech., vol. 788, 2016, 147–182). The spectral tensor of two-point second-order velocity correlations is predicted in the presence of arbitrary mean-velocity gradients and in a rotating frame. For this, we numerically solve coupled equations for the angle-dependent energy spectrum 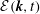${\mathcal{E}}(\boldsymbol{k},t)$ that includes directional anisotropy, and for the deviatoric pseudo-scalar 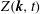$Z(\boldsymbol{k},t)$, that underlies polarization anisotropy (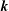$\boldsymbol{k}$ is the wavevector, $t$ the time). These equations include two parts: (i) exact linear terms representing the viscous spectral linear theory (SLT) when considered alone; (ii) generalized transfer terms mediated by two-point third-order correlations. In contrast with MCS, our model retains the complete angular dependence of the linear terms, whereas the nonlinear transfer terms are closed by a reduced anisotropic eddy damped quasi-normal Markovian (EDQNM) technique similar to MCS, based on truncated angular harmonics expansions. And in contrast with most spectral approaches based on characteristic methods to represent mean-velocity gradient terms, we use high-order finite-difference schemes (FDSs). The resulting model is applied to homogeneous rotating turbulent shear flow with several Coriolis parameters and constant mean shear rate. First, we assess the validity of the model in the linear limit. We observe satisfactory agreement with existing numerical SLT results and with theoretical results for flows without rotation. Second, fully nonlinear results are obtained, which compare well to existing direct numerical simulation (DNS) results. In both regimes, the new model improves significantly the MCS model predictions. However, in the non-rotating shear case, the expected exponential growth of turbulent kinetic energy is found only with a hybrid model for nonlinear terms combining the anisotropic EDQNM closure and Weinstock’s return-to-isotropy model.

JFM classification

Turbulent Flows: Turbulence modelling
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 866 , 10 May 2019 , pp. 5 - 32
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

André, J. C. & Lesieur, M. 1977 Influence of helicity on the evolution of isotropic turbulence at high Reynolds number. J. Fluid Mech. 81, 187–207.Google Scholar
Balbus, S. A. & Hawley, J. F. 1998 Instability, turbulence, and enhanced transport in accretion disks. Rev. Mod. Phys. 70 (1), 1–53.Google Scholar
Batchelor, G. K. 1953 The Theory of Homogeneous Turbulence. Cambridge University Press.Google Scholar
Batchelor, G. K. & Proudman, I. 1954 The effect of rapid distortion of a fluid in turbulent motion. Q. J. Mech. Appl. Maths 7 (1), 83–103.Google Scholar
Bellet, F., Godeferd, F. S., Scott, J. F. & Cambon, C. 2006 Wave turbulence in rapidly rotating flows. J. Fluid Mech. 562, 83–121.Google Scholar
Bradshaw, P. 1969 The analogy between streamline curvature and buoyancy in turbulent shear flow. J. Fluid Mech. 36 (01), 177–191.Google Scholar
Brethouwer, G. 2005 The effect of rotation on rapidly sheared homogeneous turbulence and passive scalar transport. Linear theory and direct numerical simulation. J. Fluid Mech. 542, 305–342.Google Scholar
Briard, A., Gréa, B.-J., Mons, V., Cambon, C., Gomez, T. & Sagaut, P. 2018 Advanced spectral anisotropic modelling for shear flows. J. Turbul. 19 (7), 570–599.Google Scholar
Burlot, A., Gréa, B.-J., Godeferd, F. S., Cambon, C. & Griffond, J. 2015 Spectral modelling of high Reynolds number unstably stratified homogeneous turbulence. J. Fluid Mech. 765, 17–44.Google Scholar
Cambon, C. & Jacquin, L. 1989 Spectral approach to non-isotropic turbulence subjected to rotation. J. Fluid Mech. 202, 295–317.Google Scholar
Cambon, C., Jeandel, D. & Mathieu, J. 1981 Spectral modelling of homogeneous non-isotropic turbulence. J. Fluid Mech. 104, 247–262.Google Scholar
Cambon, C., Mansour, N. N. & Godeferd, F. S. 1997 Energy transfer in rotating turbulence. J. Fluid Mech. 337, 303–332.Google Scholar
Cambon, C., Mons, V., Gréa, B.-J. & Rubinstein, R. 2017 Anisotropic triadic closures for shear-driven and buoyancy-driven turbulent flows. Comput. Fluids 151, 73–84.Google Scholar
Cambon, C. & Rubinstein, R. 2006 Anisotropic developments for homogeneous shear flows. Phys. Fluids 18 (8), 085106.Google Scholar
Canuto, V. M., Dubovikov, M. S., Cheng, Y. & Dienstfrey, A. 1996 Dynamical model for turbulence. III. Numerical results. Phys. Fluids 8 (2), 599–613.Google Scholar
Canuto, V. M. & Dubovikov, M. S. 1996a A dynamical model for turbulence. I. General formalism. Phys. Fluids 8 (2), 571–586.Google Scholar
Canuto, V. M. & Dubovikov, M. S. 1996b A dynamical model for turbulence. II. Shear-driven flows. Phys. Fluids 8 (2), 587–598.Google Scholar
Clark, T. T., Kurien, S. & Rubinstein, R. 2018 Generation of anisotropy in turbulent flows subjected to rapid distortion. Phys. Rev. E 97 (1), 013112.Google Scholar
Craya, A.1957 Contribution à l’analyse de la turbulence associée à des vitesses moyennes. PhD thesis, Université de Grenoble.Google Scholar
Dong, C., McWilliams, J. C. & Shchepetkin, A. F. 2007 Island wakes in deep water. J. Phys. Oceanogr. 37 (4), 962–981.Google Scholar
Gréa, B.-J. 2013 The rapid acceleration model and the growth rate of a turbulent mixing zone induced by Rayleigh–Taylor instability. Phys. Fluids 25 (1), 015118.Google Scholar
Hanazaki, H. & Hunt, J. C. R. 2004 Structure of unsteady stably stratified turbulence with mean shear. J. Fluid Mech. 507, 1–42.Google Scholar
Herring, J. R. 1974 Approach of axisymmetric turbulence to isotropy. Phys. Fluids 17 (5), 859–872.Google Scholar
Hiwatashi, K., Alfredsson, P. H., Tillmark, N. & Nagata, M. 2007 Experimental observations of instabilities in rotating plane Couette flow. Phys. Fluids 19 (4), 048103.Google Scholar
Johnston, J. P., Halleent, R. M. & Lezius, D. K. 1972 Effects of spanwise rotation on the structure of two-dimensional fully developed turbulent channel flow. J. Fluid Mech. 56 (03), 533–557.Google Scholar
Kassinos, S. C., Reynolds, W. C. & Rogers, M. M. 2001 One-point turbulence structure tensors. J. Fluid Mech. 428, 213–248.Google Scholar
Launder, B. E., Reece, G. Jr. & Rodi, W. 1975 Progress in the development of a Reynolds-stress turbulence closure. J. Fluid Mech. 68 (3), 537–566.Google Scholar
Leblanc, S. & Cambon, C. 1998 Effects of the coriolis force on the stability of stuart vortices. J. Fluid Mech. 356, 353–379.Google Scholar
Lesur, G. & Longaretti, P. Y. 2005 On the relevance of subcritical hydrodynamic turbulence to accretion disk transport. Astron. Astrophys. 444, 25–44.Google Scholar
Mishra, A. A. & Girimaji, S. S. 2017 Toward approximating non-local dynamics in single-point pressure–strain correlation closures. J. Fluid Mech. 811, 168–188.Google Scholar
Moffatt, H. K. 1967 The interaction of turbulence with strong wind shear. In Proceedings of the International Colloquium on Atmospheric Turbulence and Radio Wave Propagation (ed. Yaglom, A. M. & Tatarsky, V. I.), pp. 139–156. Nauka.Google Scholar
Mons, V., Cambon, C. & Sagaut, P. 2016 A spectral model for homogeneous shear-driven anisotropic turbulence in terms of spherically averaged descriptors. J. Fluid Mech. 788, 147–182.Google Scholar
Orszag, S. A. 1969 Analytical theories of turbulence. J. Fluid Mech. 41, 363–386.Google Scholar
Perret, G., Stegner, A., Farge, M. & Pichon, T. 2006 Cyclone-anticyclone asymmetry of large-scale wakes in the laboratory. Phys. Fluids 18 (3), 036603.Google Scholar
Plunian, F. & Stepanov, R. 2007 A non-local shell model of hydrodynamic and magnetohydrodynamic turbulence. New J. Phys. 9 (8), 294.Google Scholar
Pouquet, A., Lesieur, M., André, J. C. & Basdevant, C. 1975 Evolution of high Reynolds number two-dimensional turbulence. J. Fluid Mech. 72, 305–319.Google Scholar
Rogallo, R. S.1981 Numerical experiments in homogeneous turbulence. NASA Tech. Mem. 81315.Google Scholar
Rotta, J. 1951 Statistische theorie nichthomogener turbulenz i. Z. Phys. 129 (6), 547–572.Google Scholar
Sagaut, P. & Cambon, C. 2018 Homogeneous Turbulence Dynamics, 2nd edn. Springer.Google Scholar
Salhi, A. & Cambon, C. 1997 An analysis of rotating shear flow using linear theory and DNS and LES results. J. Fluid Mech. 347, 171–195.Google Scholar
Salhi, A. & Cambon, C. 2010 Stability of rotating stratified shear flow: an analytical study. Phys. Rev. E 81 (2), 026302.Google Scholar
Salhi, A., Cambon, C. & Speziale, C. G. 1997 Linear stability analysis of plane quadratic flows in a rotating frame. Phys. Fluids 9 (8), 2300–2309.Google Scholar
Salhi, A., Jacobitz, F. G., Schneider, K. & Cambon, C. 2014 Nonlinear dynamics and anisotropic structure of rotating sheared turbulence. Phys. Rev. E 89 (1), 013020.Google Scholar
Waleffe, F. 1992 The nature of triad interactions in homogeneous turbulence. Phys. Fluids A 4 (2), 350–363.Google Scholar
Weinstock, J. 1982 Theory of the pressure–strain rate. Part 2. Diagonal elements. J. Fluid Mech. 116, 1–29.Google Scholar
Weinstock, J. 2013 Analytical theory of homogeneous mean shear turbulence. J. Fluid Mech. 727, 256–281.Google Scholar
Zhu, Y.2019 Modelling and calculation for shear-driven rotating turbulence, with multiscale and directional approach. PhD thesis, École centrale de Lyon.Google Scholar