Hostname: page-component-76fb5796d-45l2p Total loading time: 0 Render date: 2024-04-25T07:01:51.370Z Has data issue: false hasContentIssue false
  • English
  • Français

Nonlinear waves with a threefold rotational symmetry in pipe flow: influence of a strongly shear-thinning rheology

Published online by Cambridge University Press:  05 April 2017

Emmanuel Plaut Open the ORCID record for Emmanuel Plaut [Opens in a new window] ,
Nicolas Roland  and
Chérif Nouar
Emmanuel Plaut*
Affiliation:
LEMTA, Université de Lorraine and CNRS, UMR 7563, Vandœuvre-lès-Nancy, 54500, France
Nicolas Roland
Affiliation:
LEMTA, Université de Lorraine and CNRS, UMR 7563, Vandœuvre-lès-Nancy, 54500, France
Chérif Nouar
Affiliation:
LEMTA, Université de Lorraine and CNRS, UMR 7563, Vandœuvre-lès-Nancy, 54500, France
*
†Email address for correspondence: emmanuel.plaut@univ-lorraine.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

In order to model the transition to turbulence in pipe flow of non-Newtonian fluids, the influence of a strongly shear-thinning rheology on the travelling waves with a threefold rotational symmetry of Faisst & Eckhardt (Phys. Rev. Lett., vol. 91, 2003, 224502) and Wedin & Kerswell (J. Fluid Mech., vol. 508, 2004, pp. 333–371) is analysed. The rheological model is Carreau’s law. Besides the shear-thinning index 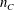$n_{C}$ , the dimensionless characteristic time $\unicode[STIX]{x1D706}$ of the fluid is considered as the main non-Newtonian control parameter. If 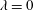$\unicode[STIX]{x1D706}=0$ , the fluid is Newtonian. In the relevant limit 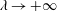$\unicode[STIX]{x1D706}\rightarrow +\infty$ , the fluid approaches a power-law behaviour. The laminar base flows are first characterized. To compute the nonlinear waves, a Petrov–Galerkin code is used, with continuation methods, starting from the Newtonian case. The axial wavenumber is optimized and the critical waves appearing at minimal values of the Reynolds number 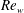$\mathit{Re}_{w}$ based on the mean velocity and wall viscosity are characterized. As 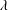$\unicode[STIX]{x1D706}$ increases, these correspond to a constant value of the Reynolds number based on the mean velocity and viscosity. This viscosity, close to the one of the laminar flow, can be estimated analytically. Therefore the experimentally relevant critical Reynolds number 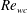$\mathit{Re}_{wc}$ can also be estimated analytically. This Reynolds number may be viewed as a lower estimate of the Reynolds number for the transition to developed turbulence. This demonstrates a quantified stabilizing effect of the shear-thinning rheology. Finally, the increase of the pressure gradient in waves, as compared to the one in the laminar flow with the same mass flux, is calculated, and a kind of ‘drag reduction effect’ is found.

JFM classification

Nonlinear Dynamical Systems: Bifurcation Non-Newtonian Flows: Non-Newtonian Flows Instability: Transition to turbulence
Type
Papers
Information
Journal of Fluid Mechanics , Volume 818 , 10 May 2017 , pp. 595 - 622
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Present address: SAFRAN, Villaroche Center, 77550 Moissy Cramayel, France.

References

Avila, M., Mellibovsky, F., Roland, N. & Hof, B. 2013 Streamwise-localized solutions at the onset of turbulence in pipe flow. Phys. Rev. Lett. 110, 224502.Google Scholar
Avila, K., Moxey, D., de Lozar, A., Avila, M., Barkley, D. & Hof, B. 2011 The onset of turbulence in pipe flow. Science 333, 192–196.Google Scholar
Avila, M., Willis, A. P. & Hof, B. 2010 On the transient nature of localized pipe flow turbulence. J. Fluid Mech. 646, 127–136.Google Scholar
Bird, B., Armstrong, R. & Hassager, O. 1987 Dynamics of Polymeric Liquids. Wiley-Interscience.Google Scholar
Carreau, J. P. 1972 Rheological equations from molecular network theories. Trans. Soc. Rheol. 16, 99–127.Google Scholar
Chantry, M., Willis, A. P. & Kerswell, R. R. 2014 Genesis of streamwise-localized solutions from globally periodic traveling waves in pipe flow. Phys. Rev. Lett. 112, 164501.CrossRefGoogle ScholarPubMed
Dennis, D. J. C. & Sogaro, F. M. 2014 Distinct organizational states of fully developed turbulent pipe flow. Phys. Rev. Lett. 113, 234501.Google Scholar
Draad, A. A., Kuiken, G. D. C. & Nieuwstadt, F. T. M. 1998 Laminar-turbulent transition in pipe flow for Newtonian and non-Newtonian fluids. J. Fluid Mech. 377, 267–312.Google Scholar
Duguet, Y., Pringle, C. C. T. & Kerswell, R. R. 2008a Relative periodic orbits in transitional pipe flow. Phys. Fluids 20, 114102.Google Scholar
Duguet, Y., Willis, A. P. & Kerswell, R. R. 2008b Transition in pipe flow: the saddle structure on the boundary of turbulence. J. Fluid Mech. 613, 255–274.Google Scholar
Eckhardt, B., Schneider, T. M., Hof, B. & Westerweel, J. 2007 Turbulence transition in pipe flow. Annu. Rev. Fluid Mech. 39, 447–468.Google Scholar
Escudier, M., Poole, R., Presti, F., Dales, C., Nouar, C., Desaubry, C., Graham, L. & Pullum, L. 2005 Observations of asymmetrical flow behaviour in transitional pipe flow of yield-stress and other shear-thinning liquids. J. Non-Newtonian Fluid Mech. 127, 143–155.CrossRefGoogle Scholar
Escudier, M. P., Presti, F. & Smith, S. 1999 Drag reduction in the turbulent pipe flow of polymers. J. Non-Newtonian Fluid Mech. 81, 197–213.Google Scholar
Escudier, M. P., Rosa, S. & Poole, R. J. 2009 Asymmetry in transitional pipe flow of drag-reducing polymer solutions. J. Non-Newtonian Fluid Mech. 161, 19–29.Google Scholar
Faisst, H. & Eckhardt, B. 2003 Traveling waves in pipe flow. Phys. Rev. Lett. 91, 224502.CrossRefGoogle ScholarPubMed
Hof, B., van Doorne, C. W. H., Westerweel, J. & Nieuwstadt, F. T. M. 2005 Turbulence regeneration in pipe flow at moderate Reynolds numbers. Phys. Rev. Lett. 95, 214502.Google Scholar
Hof, B., van Doorne, C. W. H., Westerweel, J., Nieuwstadt, F. T. M., Faisst, H., Eckhardt, B., Wedin, H., Kerswell, R. R. & Waleffe, F. 2004 Experimental observation of nonlinear traveling waves in turbulent pipe flow. Science 305, 1594–1598.Google Scholar
Jenny, M., Plaut, E. & Briard, A. 2015 Numerical study of subcritical Rayleigh–Bénard convection rolls in strongly shear-thinning Carreau fluids. J. Non-Newtonian Fluid Mech. 219, 19–34.CrossRefGoogle Scholar
Kerswell, R. R. & Tutty, O. R. 2007 Recurrence of travelling waves in transitional pipe flow. J. Fluid Mech. 584, 69–102.Google Scholar
Li, W., Xi, L. & Graham, M. D. 2006 Nonlinear travelling waves as a framework for understanding turbulent drag reduction. J. Fluid Mech. 565, 353–362.CrossRefGoogle Scholar
Liu, R. & Liu, Q. S. 2012 Nonmodal stability in Hagen–Poiseuille flow of a shear-thinning fluid. Phys. Rev. E 85, 066318.Google ScholarPubMed
López Carranza, S. N., Jenny, M. & Nouar, C. 2012 Pipe flow of shear-thinning fluids. C. R. Méc. 340, 602–618.Google Scholar
López Carranza, S. N., Jenny, M. & Nouar, C. 2013 Instability of streaks in pipe flow of shear-thinning fluids. Phys. Rev. E 88, 023005.Google Scholar
Mellibovsky, F. & Eckhardt, B. 2011 Takens-Bogdanov bifurcation of travelling-wave solutions in pipe flow. J. Fluid Mech. 670, 96–129.Google Scholar
Meseguer, A. 2003 Streak breakdown instability in pipe Poiseuille flow. Phys. Fluids 15, 1203–1213.Google Scholar
Pringle, C. C. T., Duguet, Y. & Kerswell, R. R. 2009 Highly symmetric traveling waves in pipe flow. Phil. Trans. R. Soc. Lond. A 367, 457–472.Google Scholar
Pringle, C. C. T. & Kerswell, R. R. 2007 Asymmetric, helical, and mirror-symmetric traveling waves in pipe flow. Phys. Rev. Lett. 99, 074502.Google Scholar
Roland, N., Plaut, E. & Nouar, C. 2010 Petrov–Galerkin computation of nonlinear waves in pipe flow of shear-thinning fluids: first theoretical evidences for a delayed transition. Comput. Fluids 39, 1733–1743.Google Scholar
Rudman, M., Blackburn, H. M., Graham, L. J. W. & Pullum, L. 2004 Turbulent pipe flow of shear-thinning fluids. J. Non-Newtonian Fluid Mech. 118, 33–48.CrossRefGoogle Scholar
Toms, B. A. 1948 Some observations on the flow of linear polymer solutions through straight tubes at large Reynolds numbers. In Proceedings of First International Congress on Rheology, vol. 2, pp. 135–141. North-Holland.Google Scholar
Waleffe, F. 1997 On a self-sustaining process in shear flows. Phys. Fluids 9, 883–900.Google Scholar
Waleffe, F. 1998 Three-dimensional coherent states in plane shear-flows. Phys. Rev. Lett. 81, 4140–4143.CrossRefGoogle Scholar
Wedin, H. & Kerswell, R. R. 2004 Exact coherent structures in pipe flow: travelling wave solutions. J. Fluid Mech. 508, 333–371.Google Scholar
Willis, A. P., Short, K. Y. & Cvitanović, P. 2016 Symmetry reduction in high dimensions, illustrated in a turbulent pipe. Phys. Rev. E 93, 022204.Google Scholar
Wygnanski, I. J. & Champagne, F. H. 1973 On transition in a pipe. Part 1. The origin of puffs and slugs and the flow in a turbulent slug. J. Fluid Mech. 59, 281–335.Google Scholar
Zikanov, O. Y. 1996 On the instability of pipe Poiseuille flow. Phys. Fluids 8, 2923–2932.CrossRefGoogle Scholar

Plaut Supplementary Movie

Movie 1. In a pipe section, as time goes by, velocity field of critical waves: the Newtonian EFKW wave on the left, the non-Newtonian EFKW wave nC = 0.5, λ = 18 on the right. The colors code the axial velocity, the arrows the transverse velocity. The dynamics is the same in both waves, though the center is more homogeneous and there are higher gradients near the wall in the non-Newtonian wave.

Download Plaut Supplementary Movie(Video)
Video 668.8 KB