Article contents
Non-modal stability analysis of the boundary layer under solitary waves
Published online by Cambridge University Press: 12 December 2017
Abstract
In the present work, a stability analysis of the bottom boundary layer under solitary waves based on energy bounds and non-modal theory is performed. The instability mechanism of this flow consists of a competition between streamwise streaks and two-dimensional perturbations. For lower Reynolds numbers and early times, streamwise streaks display larger amplification due to their quadratic dependence on the Reynolds number, whereas two-dimensional perturbations become dominant for larger Reynolds numbers and later times in the deceleration region of this flow, as the maximum amplification of two-dimensional perturbations grows exponentially with the Reynolds number. By means of the present findings, we can give some indications on the physical mechanism and on the interpretation of the results by direct numerical simulation in Vittori & Blondeaux (J. Fluid Mech., vol. 615, 2008, pp. 433–443) and Özdemir et al. (J. Fluid Mech., vol. 731, 2013, pp. 545–578) and by experiments in Sumer et al. (J. Fluid Mech., vol. 646, 2010, pp. 207–231). In addition, three critical Reynolds numbers can be defined for which the stability properties of the flow change. In particular, it is shown that this boundary layer changes from a monotonically stable to a non-monotonically stable flow at a Reynolds number of 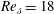 $Re_{\unicode[STIX]{x1D6FF}}=18$ .
$Re_{\unicode[STIX]{x1D6FF}}=18$ .
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 5
- Cited by


