2.1 Fluid equations

We consider the three-dimensional free-surface incompressible flow of a fluid bath of uniform density $\unicode[STIX]{x1D70C}$ , subject to gravitational and viscous forces. The domain is unbounded in all horizontal directions, is of infinite depth and the fluid is initially at rest with its free surface undisturbed. We introduce Cartesian coordinates with the positive $z$ axis pointing upwards. We also assume that the free surface can be described by a well-defined smooth function $z=\unicode[STIX]{x1D702}(x,y,t)$ . Under these assumptions the flow is governed by the Navier–Stokes equations for an incompressible fluid, i.e.

(2.1) $$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{u}_{t}+\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}=\unicode[STIX]{x1D735}\left(-{\displaystyle \frac{p}{\unicode[STIX]{x1D70C}}}\right)+\unicode[STIX]{x1D708}\unicode[STIX]{x0394}\boldsymbol{u}+\boldsymbol{g},\quad z\leqslant \unicode[STIX]{x1D702}(x,y,t) & \displaystyle\end{eqnarray}$$

(2.2) $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}=0,\quad z\leqslant \unicode[STIX]{x1D702}(x,y,t), & \displaystyle\end{eqnarray}$$

where $\boldsymbol{u}=(u^{1},u^{2},u^{3})^{\text{T}}$ and $p$ , are the velocity and pressure field, $\unicode[STIX]{x1D708}$ is the kinematic viscosity and $\boldsymbol{g}=(0,0,-g)$ is the acceleration due to gravity.

Equations (2.1) and (2.2) are subject to the condition of no motion at infinity, i.e.

(2.3) $$\begin{eqnarray}\boldsymbol{u}\rightarrow 0\quad \text{as }\sqrt{x^{2}+y^{2}+z^{2}}\rightarrow \infty .\end{eqnarray}$$

The interface is subject to surface tension and normal stresses due to the air pressure. The stress balance and the kinematic condition require, respectively, that

(2.4) $$\begin{eqnarray}\displaystyle & \displaystyle -p\;\hat{\boldsymbol{n}}+\;\unicode[STIX]{x1D749}\boldsymbol{\cdot }\hat{\boldsymbol{n}}=\left(\unicode[STIX]{x1D70E}\;\unicode[STIX]{x1D705}[\unicode[STIX]{x1D702}]-p_{s}(x,y,t)\right)\hat{\boldsymbol{n}},\quad z=\unicode[STIX]{x1D702}(x,y,t), & \displaystyle\end{eqnarray}$$

(2.5) $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D702}_{t}+\boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D735}(\unicode[STIX]{x1D702}-z)=0,\quad z=\unicode[STIX]{x1D702}(x,y,t). & \displaystyle\end{eqnarray}$$

Here $\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D70C}\unicode[STIX]{x1D708}(\unicode[STIX]{x1D735}\boldsymbol{u}+\unicode[STIX]{x1D735}\boldsymbol{u}^{\text{T}})$ , $p_{s}$ is the pressure of the air just above the free surface, $\hat{\boldsymbol{n}}=[-\unicode[STIX]{x1D702}_{x},-\unicode[STIX]{x1D702}_{y},1]^{\text{T}}/\sqrt{1+(\unicode[STIX]{x1D702}_{x})^{2}+(\unicode[STIX]{x1D702}_{y})^{2}}$ is the outward pointing unitary normal to the free surface, $\unicode[STIX]{x1D70E}$ is the surface tension coefficient and $\unicode[STIX]{x1D705}[\unicode[STIX]{x1D702}]$ is the sum of the signed principal curvatures of the free surface, which is positive for convex functions.

We recall that $p=\tilde{p}-\unicode[STIX]{x1D70C}gz$ and $\boldsymbol{g}=\unicode[STIX]{x1D735}(gz)$ , where $\tilde{p}$ is the dynamic pressure, and incorporate conservative volume forces in the pressure term. We linearise around the flat surface equilibrium $\unicode[STIX]{x1D702}(x,y,t)=0$ , which yields

(2.6a ) $$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{u}_{t}=\unicode[STIX]{x1D735}\left(-{\displaystyle \frac{\tilde{p}}{\unicode[STIX]{x1D70C}}}\right)+\unicode[STIX]{x1D708}\unicode[STIX]{x0394}\boldsymbol{u},\quad z\leqslant 0, & \displaystyle\end{eqnarray}$$

(2.6b ) $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}=0,\quad z\leqslant 0, & \displaystyle\end{eqnarray}$$

(2.6c ) $$\begin{eqnarray}\displaystyle & \displaystyle u_{z}^{1}+u_{x}^{3}=0,\quad z=0, & \displaystyle\end{eqnarray}$$

(2.6d ) $$\begin{eqnarray}\displaystyle & \displaystyle u_{z}^{2}+u_{y}^{3}=0,\quad z=0, & \displaystyle\end{eqnarray}$$

(2.6e ) $$\begin{eqnarray}\displaystyle & \displaystyle -\tilde{p}+\unicode[STIX]{x1D70C}g\unicode[STIX]{x1D702}+2\unicode[STIX]{x1D70C}\unicode[STIX]{x1D708}u_{z}^{3}=\unicode[STIX]{x1D70E}\unicode[STIX]{x1D705}[\unicode[STIX]{x1D702}]-p_{s},\quad z=0, & \displaystyle\end{eqnarray}$$

(2.6f ) $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D702}_{t}=u^{3},\quad z=0. & \displaystyle\end{eqnarray}$$

We look for solutions that satisfy the Helmholtz decomposition

(2.7) $$\begin{eqnarray}\boldsymbol{u}=\boldsymbol{v}+\boldsymbol{w},\end{eqnarray}$$

where $\boldsymbol{v}=\unicode[STIX]{x1D735}\unicode[STIX]{x1D719}$ and $\boldsymbol{w}=[w^{1},w^{2},w^{3}]^{\text{T}}=\unicode[STIX]{x1D735}\times \unicode[STIX]{x1D733}$ , with $\unicode[STIX]{x1D719}$ and $\unicode[STIX]{x1D733}$ being the scalar and vector velocity potentials, respectively. To satisfy condition (2.3), we assume that for all $t\geqslant 0$

(2.8a,b ) $$\begin{eqnarray}\unicode[STIX]{x1D719},\unicode[STIX]{x1D735}\unicode[STIX]{x1D719}\rightarrow 0\quad \text{and}\quad \unicode[STIX]{x1D733},\boldsymbol{w}\rightarrow 0,\quad \text{when }\sqrt{x^{2}+y^{2}+z^{2}}\rightarrow \infty .\end{eqnarray}$$

Substituting equation (2.7) into (2.6b ) and into (2.6a ) we obtain

(2.9a ) $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x0394}\unicode[STIX]{x1D719}=0,\quad z\leqslant 0, & \displaystyle\end{eqnarray}$$

(2.9b ) $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D735}(\unicode[STIX]{x1D719}_{t})+\boldsymbol{w}_{t}=\unicode[STIX]{x1D735}\left(-{\displaystyle \frac{\tilde{p}}{\unicode[STIX]{x1D70C}}}\right)+\unicode[STIX]{x1D708}\unicode[STIX]{x0394}\boldsymbol{w},\quad z\leqslant 0, & \displaystyle\end{eqnarray}$$

(2.10a ) $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D719}_{t}=-{\displaystyle \frac{\tilde{p}}{\unicode[STIX]{x1D70C}}},\quad z\leqslant 0, & \displaystyle\end{eqnarray}$$

(2.10b ) $$\begin{eqnarray}\displaystyle & \displaystyle w_{t}^{i}=\unicode[STIX]{x1D708}\unicode[STIX]{x0394}w^{i},\quad i=1,2,3;z\leqslant 0. & \displaystyle\end{eqnarray}$$

Moreover, substituting equations (2.7) into (2.6c ), (2.6d ) and (2.6e ) we obtain

(2.11a ) $$\begin{eqnarray}\displaystyle & \displaystyle 0=(\unicode[STIX]{x1D719}_{x}+w^{1})_{z}+(\unicode[STIX]{x1D719}_{z}+w^{3})_{x},\quad z=0, & \displaystyle\end{eqnarray}$$

(2.11b ) $$\begin{eqnarray}\displaystyle & \displaystyle 0=(\unicode[STIX]{x1D719}_{y}+w^{2})_{z}+(\unicode[STIX]{x1D719}_{z}+w^{3})_{y},\quad z=0, & \displaystyle\end{eqnarray}$$

(2.11c ) $$\begin{eqnarray}\displaystyle & \displaystyle -{\displaystyle \frac{\tilde{p}}{\unicode[STIX]{x1D70C}}}+g\unicode[STIX]{x1D702}={\displaystyle \frac{\unicode[STIX]{x1D70E}}{\unicode[STIX]{x1D70C}}}\unicode[STIX]{x1D705}[\unicode[STIX]{x1D702}]-2\unicode[STIX]{x1D708}(\unicode[STIX]{x1D719}_{z}+w^{3})_{z}-{\displaystyle \frac{p_{s}}{\unicode[STIX]{x1D70C}}},\quad z=0. & \displaystyle\end{eqnarray}$$

$x$

$y$

$i=3$

(2.12) $$\begin{eqnarray}w_{t}^{3}=2\unicode[STIX]{x1D708}\unicode[STIX]{x1D6E5}_{H}(\unicode[STIX]{x1D719}_{z}+w^{3}),\quad z=0,\end{eqnarray}$$

where $\unicode[STIX]{x1D6E5}_{H}=\unicode[STIX]{x2202}_{xx}+\unicode[STIX]{x2202}_{yy}$ and we used $w_{x}^{1}+w_{y}^{2}+w_{z}^{3}=0$ . We now combine equations (2.10a ), (2.9a ) and (2.11c ) to obtain

(2.13) $$\begin{eqnarray}\unicode[STIX]{x1D719}_{t}=-g\unicode[STIX]{x1D702}+{\displaystyle \frac{\unicode[STIX]{x1D70E}}{\unicode[STIX]{x1D70C}}}\unicode[STIX]{x1D705}[\unicode[STIX]{x1D702}]+2\unicode[STIX]{x1D708}\unicode[STIX]{x1D6E5}_{H}\unicode[STIX]{x1D719}-2\unicode[STIX]{x1D708}w_{z}^{3}-{\displaystyle \frac{p_{s}}{\unicode[STIX]{x1D70C}}},\quad z=0.\end{eqnarray}$$

We take $\unicode[STIX]{x1D70C}$ as the characteristic density, define the characteristic length $L$ , velocity $V$ and introduce the dimensionless numbers

(2.14a-c ) $$\begin{eqnarray}Fr=V^{2}/(gL),\quad We=\unicode[STIX]{x1D70C}V^{2}L/\unicode[STIX]{x1D70E}\quad \text{and}\quad Re=LV/\unicode[STIX]{x1D708},\end{eqnarray}$$

i.e. the square Froude number, Weber number and Reynolds number, respectively. Then from (2.9a ), (2.10b ), with $i=3$ , (2.6f ) and (2.7), (2.13), (2.12) and condition (2.8) we obtain a closed system which is given in dimensionless form by

(2.15a ) $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x0394}\unicode[STIX]{x1D719}=0,\quad z\leqslant 0, & \displaystyle\end{eqnarray}$$

(2.15b ) $$\begin{eqnarray}\displaystyle & \displaystyle w_{t}^{3}={\displaystyle \frac{1}{Re}}\unicode[STIX]{x0394}w^{3},\quad z\leqslant 0, & \displaystyle\end{eqnarray}$$

(2.15c ) $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D702}_{t}=\unicode[STIX]{x1D719}_{z}+w^{3},\quad z=0, & \displaystyle\end{eqnarray}$$

(2.15d ) $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D719}_{t}=-{\displaystyle \frac{1}{Fr}}\unicode[STIX]{x1D702}+{\displaystyle \frac{1}{We}}~\unicode[STIX]{x1D705}[\unicode[STIX]{x1D702}]+{\displaystyle \frac{2}{Re}}\unicode[STIX]{x1D6E5}_{H}\unicode[STIX]{x1D719}-{\displaystyle \frac{2}{Re}}w_{z}^{3}-p_{s},\quad z=0, & \displaystyle\end{eqnarray}$$

(2.15e ) $$\begin{eqnarray}\displaystyle & \displaystyle w_{t}^{3}={\displaystyle \frac{2}{Re}}\unicode[STIX]{x1D6E5}_{H}(\unicode[STIX]{x1D719}_{z}+w^{3}),\quad z=0, & \displaystyle\end{eqnarray}$$

(2.16a,b ) $$\begin{eqnarray}\unicode[STIX]{x1D719},\unicode[STIX]{x1D735}\unicode[STIX]{x1D719}\rightarrow 0\quad \text{and}\quad w^{3}\rightarrow 0,\quad \text{when }\sqrt{x^{2}+y^{2}+z^{2}}\rightarrow \infty .\end{eqnarray}$$

We also note that from (2.15c ) and (2.15e ) we have $w_{t}^{3}=2\unicode[STIX]{x1D6E5}_{H}(\unicode[STIX]{x1D702}_{t})/Re$ , at $z=0$ . Since the fluid is initially at rest and its free surface is undisturbed, this implies

(2.17) $$\begin{eqnarray}w^{3}={\displaystyle \frac{2}{Re}}\unicode[STIX]{x1D6E5}_{H}\unicode[STIX]{x1D702},\quad z=0.\end{eqnarray}$$

We substitute equations (2.7) and (2.17) into (2.6f ), and we obtain

(2.18) $$\begin{eqnarray}\unicode[STIX]{x1D702}_{t}=\unicode[STIX]{x1D719}_{z}+{\displaystyle \frac{2}{Re}}\unicode[STIX]{x1D6E5}_{H}\unicode[STIX]{x1D702},\quad z=0.\end{eqnarray}$$

We also note that (2.17) implies that $w^{3}=O(Re^{-1})$ near the free surface, and (2.15b ) implies that the boundary layer thickness scales as $Re^{1/2}$ . Thus, we rescale equation (2.15d ) more properly as

(2.19) $$\begin{eqnarray}\unicode[STIX]{x1D719}_{t}=-{\displaystyle \frac{1}{Fr}}\unicode[STIX]{x1D702}+{\displaystyle \frac{1}{We}}\unicode[STIX]{x1D705}[\unicode[STIX]{x1D702}]+{\displaystyle \frac{2}{Re}}\unicode[STIX]{x1D6E5}_{H}\unicode[STIX]{x1D719}-{\displaystyle \frac{2}{Re^{3/2}}}w_{z}^{3}-p_{s},\quad z=0.\end{eqnarray}$$

Finally, we recall our high-Reynolds-number assumption and disregard the term of highest order in $(1/Re)$ in (2.19). Combining this with (2.15a ), (2.18), and the condition (2.16) we obtain the dimensionless system

(2.20a ) $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x0394}\unicode[STIX]{x1D719}=0,\quad z\leqslant 0, & \displaystyle\end{eqnarray}$$

(2.20b ) $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D702}_{t}={\displaystyle \frac{2}{Re}}\unicode[STIX]{x1D6E5}_{H}\unicode[STIX]{x1D702}+\unicode[STIX]{x1D719}_{z},\quad z=0, & \displaystyle\end{eqnarray}$$

(2.20c ) $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D719}_{t}=-{\displaystyle \frac{1}{Fr}}\unicode[STIX]{x1D702}+{\displaystyle \frac{1}{We}}\unicode[STIX]{x1D705}[\unicode[STIX]{x1D702}]+{\displaystyle \frac{2}{Re}}\unicode[STIX]{x1D6E5}_{H}\unicode[STIX]{x1D719}-p_{s},\quad z=0; & \displaystyle\end{eqnarray}$$

(2.21) $$\begin{eqnarray}\unicode[STIX]{x1D719},\unicode[STIX]{x1D735}\unicode[STIX]{x1D719}\rightarrow 0\quad \text{when }\sqrt{x^{2}+y^{2}+z^{2}}\rightarrow \infty .\end{eqnarray}$$

2.1.1 Reducing the fluid system to the boundary

We note that (2.20b ) and (2.20c ) require the evaluation of function $\unicode[STIX]{x1D719}$ and $\unicode[STIX]{x1D719}_{z}$ only on the boundary plane $z=0$ . $\unicode[STIX]{x1D719}_{z}$ is the normal derivative at the boundary, of the solution of the Laplace problem in the half-space with the decay conditions (2.21). We can write

(2.22) $$\begin{eqnarray}\unicode[STIX]{x1D719}_{z}=N(\unicode[STIX]{x1D719}),\end{eqnarray}$$

where $N$ is the linear Dirichlet to Neumann map, which is well defined in this domain for a smooth function $\unicode[STIX]{x1D719}$ that decays sufficiently fast at infinity. In fact, its expression is given by the principal value of a singular integral, namely

(2.23) $$\begin{eqnarray}N\unicode[STIX]{x1D719}(\boldsymbol{r})={\displaystyle \frac{1}{2\unicode[STIX]{x03C0}}}\lim _{\unicode[STIX]{x1D716}\rightarrow 0^{+}}\displaystyle \int _{\mathbb{R}^{2}\setminus B\left(\boldsymbol{r};\unicode[STIX]{x1D716}\right)}{\displaystyle \frac{\unicode[STIX]{x1D719}(\boldsymbol{r})-\unicode[STIX]{x1D719}(\boldsymbol{s})}{|\boldsymbol{r}-\boldsymbol{s}|^{3}}}\,\text{d}A(\boldsymbol{s}),\end{eqnarray}$$

where $\boldsymbol{r}=(x,y)$ , $\boldsymbol{s}=(x^{\prime },y^{\prime })$ and $B(\boldsymbol{r};\unicode[STIX]{x1D716})=\{\boldsymbol{s}=(x^{\prime },y^{\prime }),|\boldsymbol{r}-\boldsymbol{s}|<\unicode[STIX]{x1D716}\}$ .

In appendix A, we prove that under our working assumptions a function $\unicode[STIX]{x1D719}$ with a relative weak decay must satisfy equation (2.23). We also show that the singular integral in (2.23) converges wherever $\unicode[STIX]{x1D719}$ is smooth.

The considerations above reduce the problem of calculating the surface evolution to solving

(2.24a ) $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D702}_{t}={\displaystyle \frac{2}{Re}}\unicode[STIX]{x1D6E5}_{H}\unicode[STIX]{x1D702}+N\unicode[STIX]{x1D719},\quad z=0, & \displaystyle\end{eqnarray}$$

(2.24b ) $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D719}_{t}=-{\displaystyle \frac{1}{Fr}}\unicode[STIX]{x1D702}+{\displaystyle \frac{1}{We}}\unicode[STIX]{x1D705}[\unicode[STIX]{x1D702}]+{\displaystyle \frac{2}{Re}}\unicode[STIX]{x1D6E5}_{H}\unicode[STIX]{x1D719}-p_{s},\quad z=0; & \displaystyle\end{eqnarray}$$

subject to

(2.25a ) $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D702}\rightarrow 0,\quad \text{when }(x,y)\rightarrow \infty , & \displaystyle\end{eqnarray}$$

(2.25b ) $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D719}\rightarrow 0,\quad \text{when }(x,y,z)\rightarrow \infty . & \displaystyle\end{eqnarray}$$

2.2 Interaction with the solid

We can describe the vertical position $h^{c}$ of the centre of mass of the solid by

(2.26) $$\begin{eqnarray}h_{tt}^{c}=-g-{\displaystyle \frac{c_{f}}{m}}h_{t}^{c}+{\displaystyle \frac{1}{m}}\int _{A_{C}}p_{s}\,\text{d}A,\end{eqnarray}$$

where $m$ is the mass of the solid; $A_{C}$ is the normal projection, on the horizontal plane, of the portion of the solid that is in contact with the surface (see figure 1) and $c_{f}$ incorporates the effects of friction of the ball with the air. In general, the dependence of $c_{f}$ on the velocity of the solid, proximity to the free surface and other physical parameters can be very elaborate (Brenner Reference Brenner1961). In many cases it can be disregarded altogether or approximated simply, such as by using Stokes’ drag (Moláček & Bush Reference Moláček and Bush2013a ) for the flight of bouncing droplets. Here, for consistency with prior work, despite its effect being small as $c_{f}V/mg\ll 1$ , we use Stokes’ drag in the bouncing droplet case, and set $c_{f}=0$ in the solid impact case, as the sphere’s velocity is imposed at impact.

Figure 1. Schematics of an axial section of the hydrophobic impact of a solid sphere onto a free fluid surface. The unpressed free surface is shown in the dashed light grey line, the pressed part of the fluid interface $S_{C}$ is shown in dark grey. The dashed line sits on the level of the undisturbed free surface ( $z=0$ ), and its length corresponds to the diameter of $A_{C}$ (i.e. $2r_{c}$ ), the normal projection of the pressed spherical cap $S_{C}$ on the horizontal plane.

Similar equations can be formulated for horizontal motion of the solid, as well as for its rotation. However, at this stage, we decide to limit our study to the case of axisymmetric solids impacting on axisymmetric free surfaces. This removes the need to calculate the rotation and the horizontal motion of the solid. Moreover, the height of the lowest point of the solid body $h$ , which lies on the symmetry axis (as a consequence of symmetry and convexity, see figure 1) is given by a vertical translation of $h^{c}$ .

We are imposing that the pressure applied on both impacting surfaces is the same; this means that, if there exists a thin air layer separating the two, the pressure across it does not change, consistent with lubrication theory. We will also assume that air pressure above the surface $p_{s}(r,t)$ is only different from zero on $A_{C}$ . We write equation (2.26) for $h$ and in dimensionless form and obtain

(2.27) $$\begin{eqnarray}h_{tt}=-{\displaystyle \frac{1}{Fr}}-Dh_{t}+{\displaystyle \frac{1}{M}}\int _{A_{C}}p_{s}\,\text{d}A,\end{eqnarray}$$

where $D=c_{f}L/(mV^{2})$ and $M=m/\unicode[STIX]{x1D70C}L^{3}$ .

We assume that the bottom part of the solid body is described by a function $z_{s}$ , with smooth curvature in the vicinity of the impacting region. We recall that the problem is axisymmetric, and thus we define a radial coordinate system given by $r=\sqrt{x^{2}+y^{2}~}$ . Since functions of $(x,y)$ are simply functions of $r$ , the main constraint for the fluid–solid interaction can then be stated as

(2.28) $$\begin{eqnarray}\unicode[STIX]{x1D702}(r,t)\leqslant h(t)+z_{s}(r),\end{eqnarray}$$

which must hold everywhere under the solid, and where we assume $z_{s}(0)=0$ .

We impose a second natural constraint, namely that the contact angle, at the boundary of the pressed surface $S_{C}$ (see figure 1), has to be $\unicode[STIX]{x03C0}$ . This assumption is equivalent to stating that the effect of surface tension at the boundary of $S_{C}$ is exactly equal to the effect of the jump in pressure due to the curvature of $S_{C}$ . This can be seen using the method presented in Keller (Reference Keller1998), with the difference that integrations in this case need to be carried out in the contact area and not outside of it.

We ignore the dynamics of air and thus identify $A_{C}$ as the region of the $z=0$ plane where relation (2.28) is satisfied as an equality. In practice, this means that there will be no distinction between the pressed part of the free surface and that of the solid. Figure 1 might induce the reader to think that there in fact exists a difference in height between the two pressed surface portions, however this is not the case in the model. The separation shown in figure 1 serves merely didactic purposes.

We thus wish to solve equations (2.24) and (2.27) subject to conditions (2.25), (2.28) and that the surface is tangent to the solid at the contact line. Based on our symmetry and convexity assumptions, we have that $A_{C}$ must be a disc. An important particularity of the system given by (2.24) and (2.27) is that we do not have a law for the evolution of $A_{C}$ , i.e. we do not have an a priori estimate of where to apply pressure at a future time. This scenario suggests a method that iterates on the radius of $A_{C}$ and verifies the constraint (2.28) and the tangency condition on the boundary of $A_{C}$ . Moreover pressure values, to be calculated across $A_{C}$ , must be such as to enforce that the condition (2.28) is satisfied in the form of an equality over $A_{C}$ . However, $\unicode[STIX]{x1D702}$ and $h$ are unknown; strongly suggesting the need for an implicit iterative method.

We have purposely not linearised the curvature of the free surface $\unicode[STIX]{x1D705}[\unicode[STIX]{x1D702}]$ in (2.24b ). Under the solid we shall use the full curvature. This does not pose a mathematical difficulty, as a jump in curvature is expected at a contact line. Further, the resultant force on a wetted solid can be computed as an integral along the contact curve. This integral, as the contact angle tends to $\unicode[STIX]{x03C0}$ , converges to the Young–Laplace pressure jump integrated over the wetted area (Keller Reference Keller1998). We linearise the curvature on the free surface, as this removes the need to implement a nonlinear solver in the numerical scheme. In what follows, we assume $\unicode[STIX]{x1D705}[\unicode[STIX]{x1D702}]\approx \unicode[STIX]{x1D6E5}_{H}$ outside of $A_{C}$ , and the exact curvature of the sphere ( $\unicode[STIX]{x1D705}=2/R_{o}$ ) on the contact area.

The problem is now reduced to solving

(2.29a ) $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D702}_{t}={\displaystyle \frac{2}{Re}}\unicode[STIX]{x1D6E5}_{H}\unicode[STIX]{x1D702}+N\unicode[STIX]{x1D719}, & \displaystyle\end{eqnarray}$$

(2.29b ) $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D719}_{t}=-{\displaystyle \frac{1}{Fr}}\unicode[STIX]{x1D702}+{\displaystyle \frac{1}{We}}\unicode[STIX]{x1D6E5}_{H}\unicode[STIX]{x1D702}+{\displaystyle \frac{2}{Re}}\unicode[STIX]{x1D6E5}_{H}\unicode[STIX]{x1D719}-p_{s}+{\displaystyle \frac{1}{We}}(\unicode[STIX]{x1D705}-\unicode[STIX]{x1D6E5}_{H})\unicode[STIX]{x1D702}, & \displaystyle\end{eqnarray}$$

(2.29c ) $$\begin{eqnarray}\displaystyle & \displaystyle h_{tt}=-{\displaystyle \frac{1}{Fr}}-Dh_{t}+{\displaystyle \frac{1}{M}}\int _{r\leqslant r_{c}}p_{s}\,\text{d}A, & \displaystyle\end{eqnarray}$$

$z=0$

(2.30a ) $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D702}<h+z_{s},\quad \text{where }r_{c}<r<R_{o}; & \displaystyle\end{eqnarray}$$

(2.30b ) $$\begin{eqnarray}\displaystyle & \displaystyle p_{s}=0,\quad \text{where}\;r>r_{c}; & \displaystyle\end{eqnarray}$$

(2.30c ) $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D702}=h+z_{s},\quad \text{where }r\leqslant r_{c}; & \displaystyle\end{eqnarray}$$

(2.30d ) $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x2202}_{r}\unicode[STIX]{x1D702}(r_{c})=\unicode[STIX]{x2202}_{r}z_{s}(r_{c}), & \displaystyle\end{eqnarray}$$

$r_{c}$

$R_{o}$

$\unicode[STIX]{x1D705}$

$\unicode[STIX]{x1D6E5}_{H}$

4.1 Solid spheres impacting a quiescent bath

We consider a perfectly hydrophobic solid sphere of density $\unicode[STIX]{x1D70C}_{s}$ , impacting normally onto the free surface of a quiescent bath and assume that the drag due to the air as the ball impacts the bath is negligible when compared to the other forces at work during impact, i.e. $D=0$ in (2.27). Thus, defining $L$ and $V$ , in (2.14), as $R_{o}$ (radius of the solid sphere) and $V_{0}$ (incoming velocity), the four dimensionless numbers that characterise the system, are $Re=R_{o}V_{0}/\unicode[STIX]{x1D708}$ , $Fr=V_{0}^{2}/(gR_{o})$ , $We=\unicode[STIX]{x1D70C}V_{0}^{2}R_{o}/\unicode[STIX]{x1D70E}$ and $M=4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{s}/(3\unicode[STIX]{x1D70C})$ .

We choose the radial discretisation so as to guarantee at least 40 mesh points over the unit length of the ball’s radius and a domain of computation greater than $10$ such units and verify that during the numerical experiments the waves are negligible near its boundary. We use cubic interpolation for the radial function $\unicode[STIX]{x1D719}$ to estimate operator $N$ . We initially test the method by solving for all possible discrete contact lengths at each time step, i.e. taking $k=0,1,2,\ldots ,k_{max}$ , with $k_{max}$ equal to the integer part of $R_{o}/\unicode[STIX]{x1D6FF}r+1$ . We accept as the solution, among those which satisfy condition (2.28), the one which minimises the tangency error in absolute value. Figure 2 illustrates this point; figure 2(a) corresponds to using $r_{c}$ too small, which typically produces a small tangency error but violates condition (2.28) (note that the fluid is overlapping with the sphere). Figure 2(b) corresponds to satisfying condition (2.28) and panel 2(c) also satisfies (2.28) but with a much larger mismatch in tangency. The minimum absolute tangency error is usually achieved by the smallest $r_{c}$ that satisfies condition (2.28).

Figure 2. Typical tangency error behaviour. All images correspond to the same simulation at the same time and the axes are in units of ball radii: (a) a contact in which $r_{c}$ is too small; (b) the optimal radius $r_{c}$ for the given discretisation; and (c) $r_{c}$ being too large.

We notice that successive reductions of the time step indicate that the change of $r_{c}$ in time is continuous; never skipping a neighbouring discrete value, provided the time step is sufficiently small. The evidenced continuous nature of $r_{c}$ in time, together with the fast changes in velocity observed for stronger impacts, induce the choice of an adaptive time step method. Moreover, recording the error in tangency at each tested value of $r_{c}$ provides evidence that the tangency error behaves monotonically with the error in $r_{c}$ . That is to say that, for radii that are smaller than the optimal, the surface of the fluid has a greater slope than that of the solid ball at $r_{c}$ , while for larger radii the situation is reversed. Figure 2 illustrates this situation.

Based on the monotonicity of the tangency error, and on its continuity in time, we can test at each time step the previous value of $r_{c}$ , then test a neighbouring value to identify the direction of error decrease, and test values of $r_{c}$ simply following the gradient. If the minimum of the error is farther than $\unicode[STIX]{x1D6FF}r$ away from the previous value, we repeat the calculation with a $\unicode[STIX]{x1D6FF}t$ that is halved. We do this recursively until we are able to track the motion of the contact front to increases of one mesh intervals at each $\unicode[STIX]{x1D6FF}t$ . We thus need only test at most $4$ possible values of $r_{c}$ at each attempt to use a given time step before reducing it if necessary (two tests to determine direction of improvement and at most two more to verify that the next one in that direction is a local minimum of error). We impose an extra condition on the time steps, if the previous successful time step used was smaller than an initially prescribed value, for the next time step we will use, at most, twice its value. This allows for a relatively smooth variation of time steps, while we also require that a maximum time step is not surpassed.

4.1.1 Comparisons to experiments

Experimental data on solid balls covered with a superhydrophobic coating are reported in Lee & Kim (Reference Lee and Kim2008). Comparisons between our simulations and these experimental results support the validity of our model. Figure 4 of Lee & Kim (Reference Lee and Kim2008) presents a vertical tracking of the centre of a hydrophobic ball as it impacts on the free surface of water. Figure 3(a) compares our simulation results for the same configuration. The solid curves correspond to the simulation of the same experiment assuming standard values of physical properties of pure water at $25\,^{\circ }\text{C}$ (see appendix C). Figure 3(b) shows the temporal evolution of the total upward force on the droplet during impact, as well as its comparison with the fraction of this force that is due to surface tension. Figure 3(b) is consistent with the notion that inertia is the main force during the first stages of impact, as is assumed in the Wagner model, and also shows that at the scale we are working, surface tension becomes more important as the impact continues. It is, in fact, the most relevant effect during lift off, since removing it would reverse the sign of the force. Forces due to hydrostatic effects are small, in comparison, throughout the whole impact. It is important to highlight that the vertical trajectory obtained from the experiments reported in Lee & Kim (Reference Lee and Kim2008) deforms the surface substantially (over a full diameter), and hence one might expect a model based on a linearisation of the free surface to differ substantially from experimental results. This is certainly not the case, as shown in figures 3(a) and 4, where we see that agreement is excellent, with the possible exception of lift off behaviour. This discrepancy could be due to a cumulative effect which results from linearising the fluid equations.

Figure 3. (a) Comparison of experimental results to our simulations of the same experiment. Markers ( $+$ ) correspond to the tracking of the centre of the ball as reported in figure 4 of Lee & Kim (Reference Lee and Kim2008) ( $R_{o}=0.96~\text{mm}$ , $V_{0}=89~\text{cm}~\text{s}^{-1}$ , $\unicode[STIX]{x1D70C}_{s}=1.32~\text{gr}~\text{cm}^{-3}$ ; i.e. $Re=955.7$ , $Fr=84.2$ , $We=10.71$ , $M=5.5$ ), solid curves correspond to the results of our simulation. The black curve shows the vertical trajectory of the centre of the ball, the dark grey curve tracks the south pole of the ball and the light grey curve displays the elevation of the fluid free surface just underneath the same point. The grey curves coincide while in contact. (b) Vertical upward force on the ball (black) as predicted by the model. In grey we have the contribution to this force that is due to the pressure jump imposed by surface tension.

Figure 4. Cross-sections of the simulation and experimental results. The grey circle corresponds to the experimental tracking of the ball as reported in figure 4 of Lee & Kim (Reference Lee and Kim2008): (a) $tV_{0}/R_{o}=2$ ; (b) $tV_{0}/R_{o}=4$ ; (c) $tV_{0}/R_{o}=8$ ; (d) $tV_{0}/R_{o}=18$ .

4.2 Bouncing droplets

We model the successive impacts of a bouncing droplet using the method presented here. To this end, we treat the drop as a rigid sphere, and apply at each impact the method described in the previous sections and the appendices. However, some adaptations are required. First, we follow Milewski et al. (Reference Milewski, Galeano-Rios, Nachbin and Bush2015) in introducing a viscosity correction to the fluid model ( $\unicode[STIX]{x1D708}^{\ast }=0.8025\unicode[STIX]{x1D708}$ ), which essentially adjusts dissipation so as to match the experimental Faraday threshold of the low viscosity silicone oil experiments that we model. Second, characteristic length and time scales of the fluid motion are no longer set by the size of the drop, instead they are determined by the scale of the Faraday waves, which are subharmonic to the forcing. Namely, $L=\unicode[STIX]{x1D706}_{F}$ and $V=\unicode[STIX]{x1D706}_{F}f_{F}$ ; wavelength and phase velocity, respectively. Here we use $\unicode[STIX]{x1D706}_{F}=0.4969~\text{cm}$ , which corresponds to the corrected viscosity model for this fluid equations (Milewski et al. Reference Milewski, Galeano-Rios, Nachbin and Bush2015). This yields

(4.1a-e ) $$\begin{eqnarray}Fr={\displaystyle \frac{\unicode[STIX]{x1D706}_{F}f_{F}^{2}}{g}}\text{, }~We={\displaystyle \frac{\unicode[STIX]{x1D70C}\unicode[STIX]{x1D706}_{F}^{3}f_{F}^{2}}{\unicode[STIX]{x1D70E}}},~~Re={\displaystyle \frac{\unicode[STIX]{x1D706}_{F}^{2}f_{F}}{\unicode[STIX]{x1D708}^{\ast }}},\quad D={\displaystyle \frac{9\unicode[STIX]{x1D707}_{air}}{2\unicode[STIX]{x1D70C}R_{o}^{2}f_{F}}}\quad \text{and}\quad M={\displaystyle \frac{4\unicode[STIX]{x03C0}R_{o}^{3}}{3\unicode[STIX]{x1D706}_{F}^{3}}}.\end{eqnarray}$$

Moreover, we solve the system in the non-inertial frame of reference of the shaking bath, this implies we must introduce a time-dependent oscillatory term to the gravity field. Thus, we multiply the dimensionless number $1/Fr$ in (2.29b ) and (2.29c ) by

(4.2) $$\begin{eqnarray}(1-\unicode[STIX]{x1D6E4}\cos (\unicode[STIX]{x1D714}_{0}t+\unicode[STIX]{x1D703}_{0})).\end{eqnarray}$$

We also include friction due to air, which we approximate using Stokes’ drag on a sphere, and change the size of the radial mesh intervals to a tenth of the droplet radius, as the need to calculate repeated impacts would turn our original mesh excessively time consuming. Another reason to accept this coarser mesh is simply that in this problem deflections are much smaller, consequently fewer points produce a good approximation of the surface shape. In contrast, the domain size in this problem needs to be large enough as the standing waves are spatially extended. Consequently, we define our circular domain of computation to be of $10$ Faraday wavelengths in radius, this choice proved to be sufficient to produce waves that vanish at the boundary for all regimes presented in the work of Milewski et al. (Reference Milewski, Galeano-Rios, Nachbin and Bush2015).

Figure 5. Cross-section of the bouncer’s impact ( $\unicode[STIX]{x1D6E4}=3.25$ , $\unicode[STIX]{x1D6FA}=0.8$ ). The solid grey line corresponds to the free surface, the dashed line shows the undisturbed surface level. Axes are measured in millimetres.

In order to produce simulation results that can be compared later to experimental results, we simulate the configuration of $20~\text{cSt}$ silicone oil and 80 Hz shaking used in Wind-Willansen et al. (Reference Wind-Willansen, Moláček, Harris and Bush2013), i.e. $Fr=0.81$ , $We=9.04$ and $Re=61.54$ ; more details on this configuration are given in appendix C. We run simulations that correspond to $240$ forcing periods ( $T_{f}$ ), which guaranteed attaining a steady regime. We follow Gilet & Bush (Reference Gilet and Bush2009) in their notation of bouncing modes defined by ordered pairs $(m,n)$ , in which $m$ describes the period of vertical motion in units of $T_{f}$ and $n$ stands for the number of contacts intervals that droplet and bath sustain in one period of vertical motion. They also introduce two different $(2,1)$ modes, namely $(2,1)^{1}$ and $(2,1)^{2}$ , which are qualitatively different. Following Dorbolo et al. (Reference Dorbolo, Terwagne, Vandewalle and Gilet2008) and Wind-Willansen et al. (Reference Wind-Willansen, Moláček, Harris and Bush2013), we also classify our droplets in terms of their vibration number $\unicode[STIX]{x1D6FA}=\unicode[STIX]{x1D714}_{0}\sqrt{\unicode[STIX]{x1D70C}R_{o}^{3}/\unicode[STIX]{x1D70E}}$ . In practice, $\unicode[STIX]{x1D6FA}$ is a proxy for droplet radius $R_{o}$ , since the other variables that define $\unicode[STIX]{x1D6FA}$ (fluid properties and forcing frequency) are fixed by the experimental set-up.

With this model we are able to reproduce most features of the bouncing droplet phenomena. Surface waves are triggered by the successive impacts of the droplets, and experimentally observed modes of bouncing arise spontaneously, without resorting to the parametrisation of impact used in Moláček & Bush (Reference Moláček and Bush2013a ) and Milewski et al. (Reference Milewski, Galeano-Rios, Nachbin and Bush2015).

Figure 6. Wave profiles during one forcing period (a), sampled evenly through time. The grey contour limits the region that is blown up in (b), showing the details of the forced part of the surface. In (b) the contact area is highlighted with a thicker grey line. Time increases in the vertical direction; $\unicode[STIX]{x1D6FA}=0.8$ and $\unicode[STIX]{x1D6E4}=3.25$ . The grey vertical bars on both panels are placed there for scaling, and their extent is of 0.1 mm.

Figure 5 illustrates the details of a characteristic impact of the bouncing droplet on to the fluid surface. This figure shows the great difference in curvature between the free surface and the pressed surface $S_{C}$ . Figure 6 shows this more emphatically. In this figure, the vertical scale is exaggerated with the purpose of making small surface waves visible. On the scale of the waves the curvature of the droplet appears as a sharp cusp, see figure 6(a), this finding is consistent with observations made in previous studies, see Gilet (Reference Gilet2014). In figure 6(b), the highlighting of the contact area illustrates the motivation to use the full nonlinear curvature where the droplet presses against the free surface, and its linear approximation everywhere else.

Modes of bouncing are often identified in experimental work by taking a single pixel vertical slice of the high-speed videos and placing them side by side from left to right in order of increasing time, which facilitates somewhat the identification of contacts (Protière, Boudaoud & Couder Reference Protière, Boudaoud and Couder2006; Wind-Willansen et al. Reference Wind-Willansen, Moláček, Harris and Bush2013; Terwagne et al. Reference Terwagne, Ludewig, Vandewalle and Dorbolo2013). The analogue plot in this model consists of the trajectory of the south pole of the droplet and the central point of our free surface. Figure 7 shows characteristic plots for some of the bouncing modes we have found.

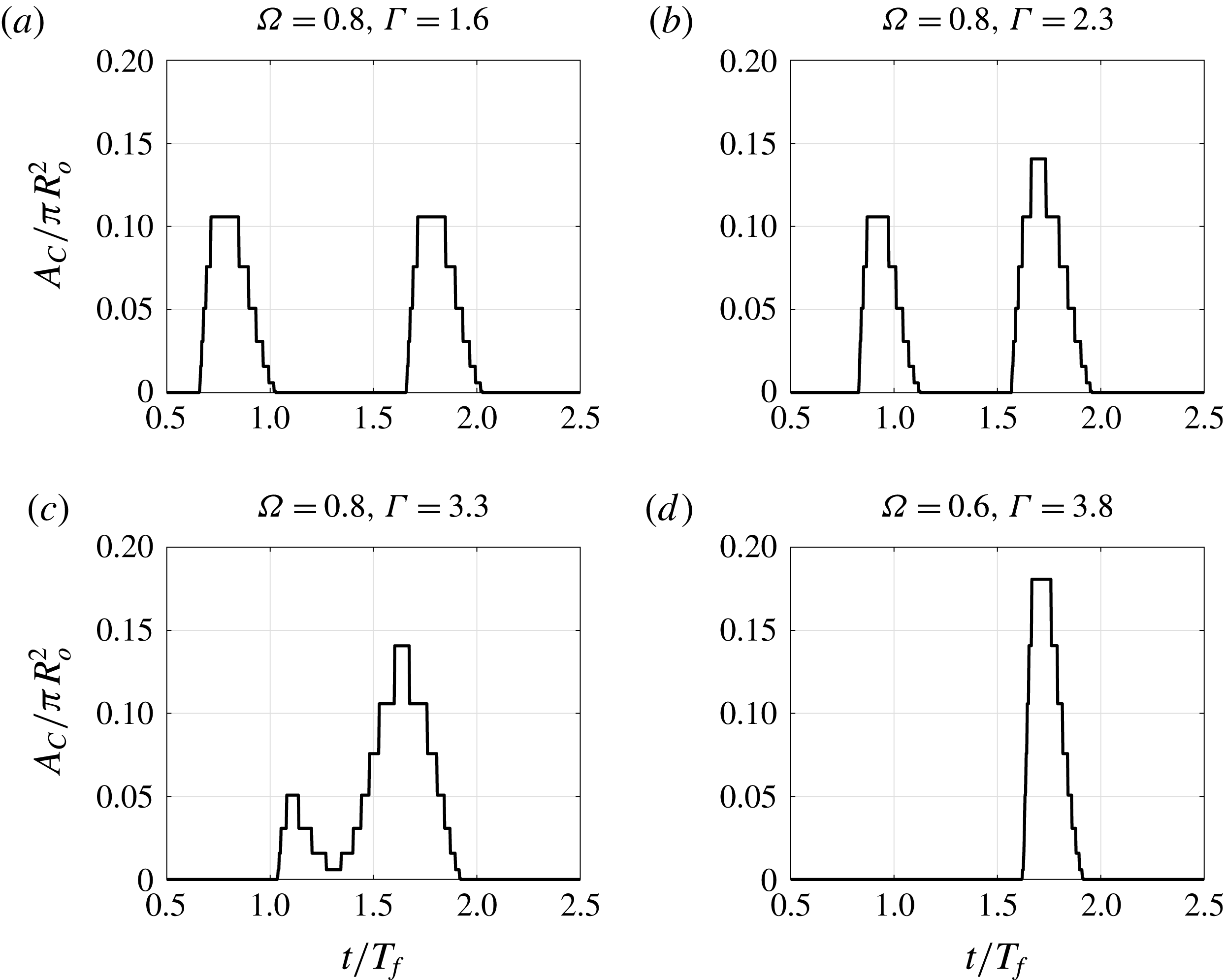
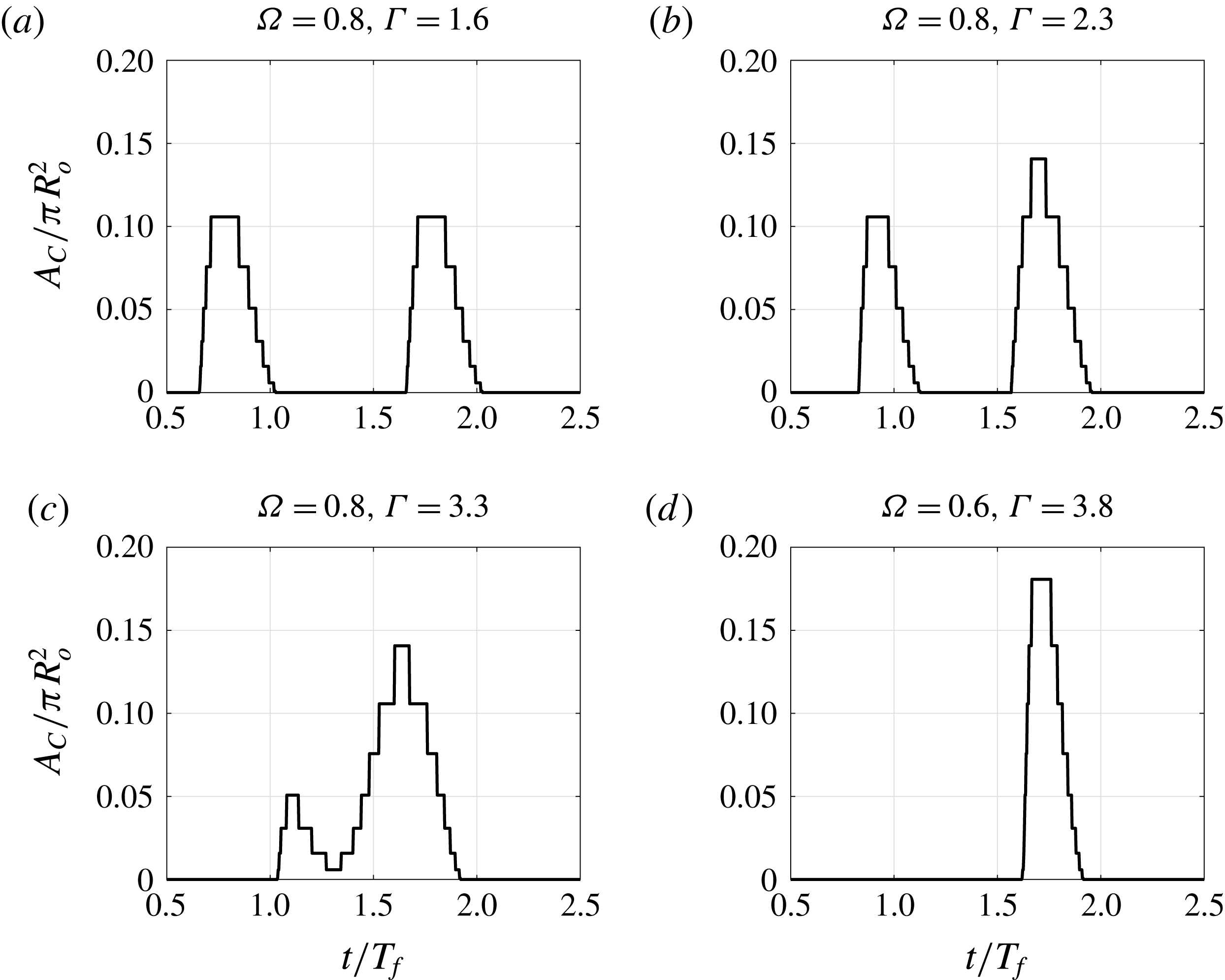
This model predicts the pressure field under the drop during contact. Integrating this field in space we obtain the value of the force that is applied to the droplet. Figure 8 shows the prediction of the force on the droplet throughout two forcing periods. We notice that, as expected, surface tension contributes a substantial amount to the vertical impulse on the droplet.

Figure 7. Motion of the south pole of the drop (black) and the fluid point just underneath it (grey). Bouncing modes can be identified from the figures: (a) a $(1,1)$ mode, (b) a $(2,2)$ , (c) a slightly different $(2,2)$ mode, (d) a $(2,1)^{1}$ mode, (e) a $(2,1)^{2}$ mode and (f) a chaotic mode.

Figure 8 also shows a comparison with the predictions of the parameterised model presented in Milewski et al. (Reference Milewski, Galeano-Rios, Nachbin and Bush2015), which is based on the spring model developed in Moláček & Bush (Reference Moláček and Bush2013a ). We note that there is an mistake in an equation used in Milewski et al. (Reference Milewski, Galeano-Rios, Nachbin and Bush2015), carried over from a typographical error in (3.7) and (A 14) of Moláček & Bush (Reference Moláček and Bush2013a ). In the denominator of the coefficient of the damping term of (2.42) in Milewski et al. (Reference Milewski, Galeano-Rios, Nachbin and Bush2015), the logarithm should be squared. Thus, the equation should read

(4.3) $$\begin{eqnarray}\left(1+{\displaystyle \frac{c_{3}}{\ln ^{2}\left|{\displaystyle \frac{c_{1}R_{0}}{Z-\bar{\unicode[STIX]{x1D702}}}}\right|}}\right)m{\displaystyle \frac{\text{d}^{2}Z}{\text{d}t^{2}}}+{\displaystyle \frac{4}{3}}{\displaystyle \frac{\unicode[STIX]{x03C0}\unicode[STIX]{x1D708}\unicode[STIX]{x1D70C}R_{0}c_{2}}{\ln ^{2}\left|{\displaystyle \frac{c_{1}R_{0}}{Z-\bar{\unicode[STIX]{x1D702}}}}\right|}}{\displaystyle \frac{\text{d}}{\text{d}t}}(Z-\bar{\unicode[STIX]{x1D702}})+{\displaystyle \frac{2\unicode[STIX]{x03C0}\unicode[STIX]{x1D70E}}{\ln \left|{\displaystyle \frac{c_{1}R_{0}}{z-\bar{\unicode[STIX]{x1D702}}}}\right|}}(Z-\bar{\unicode[STIX]{x1D702}})=-m~g(t).\end{eqnarray}$$

In what follows we have recomputed the solutions of Milewski et al. (Reference Milewski, Galeano-Rios, Nachbin and Bush2015) using the correct equation. Overall, in our limited tests, this correction introduces only relatively small changes in behaviour in the regimes considered here. Since the term appears correctly in (A 13) in the appendix of Moláček & Bush (Reference Moláček and Bush2013a ), we do not believe that their results are affected.

We recall this spring model was derived assuming a constant contact area underneath the droplet and without a kinematic constraint imposing that the surface deflection had to be consistent with the motion of the droplet (although the behaviour, verified a posteriori was reasonable). Both methods predict a fast rise in the forces at the initial stages of contact, followed by a slower decay until take off. We also show the decomposition of the total force on the drop, providing insight on which forces are more important at each stage of impact (inertial versus surface tension). As in the case of the fast impact of a solid ball, discussed in the previous section, both inertia and surface tension play a significant role. At the initial stages of impact, in the cases considered; inertia contributes approximately as much as surface tension, whilst at later stages capillary effects are dominant. Moreover, figure 8 provides evidence on how the impacts change as $\unicode[STIX]{x1D6E4}$ increases (also seen in figure 11). The transition from the $(1,1)$ to the $(2,2)$ mode takes place when the first impact occurs later and the second impact earlier, breaking the $(1,1)$ mode symmetry. Continuing this process, the first impact becomes less important and the second one more until they merge, giving rise to a stronger single impact in the $(2,1)$ mode.

Figure 8. Forces between the drop and the bath during two periods of forcing: (a) a $(1,1)$ mode, (b) a $(2,2)$ mode, (c) a $(2,1)^{1}$ mode and (d) a $(2,1)^{2}$ mode. Solid black lines correspond to the prediction of the forces as given by the present model. Grey dashed lines show the forces for the same regimes, as predicted by Milewski et al. (Reference Milewski, Galeano-Rios, Nachbin and Bush2015), grey solid lines trace the contribution of surface tension to the total force. We recall that $m$ is the mass of the droplet.

Figure 9. Evolution of the contact area ( $A_{C}$ ) over two forcing periods. (a–d) Correspond to the bouncing regimes depicted in figure 8 in the respective panels. We note that for this figure and figure 8 we used $\text{d}r\leqslant R_{o}/20$ .

Figure 9 shows the evolution of the contact area in the same cases for which the force was depicted in figure 8. Since the curvature of the sphere is constant, the contact area determines the contribution of surface tension to the vertical force on the drop (shown in solid grey lines in figure 8).

4.2.1 Comparisons to experiments

We map the steady state regimes that we observe in the simulations on the $\unicode[STIX]{x1D6E4}$ – $\unicode[STIX]{x1D6FA}$ plane against the corresponding experimental data points found in Wind-Willansen et al. (Reference Wind-Willansen, Moláček, Harris and Bush2013), see figure 10. We include a hashed area in this figure, which corresponds to the mode shown in figure 7(c). This mode of bouncing, whilst according to the definition is a $(2,2)$ mode, might easily be mistaken for a $(2,1)^{1}$ mode, since the two contacts are only briefly separated by a short time in which the droplet hovers over the free surface. In fact, for $\unicode[STIX]{x1D6FA}=0.8$ , data from Wind-Willansen et al. (Reference Wind-Willansen, Moláček, Harris and Bush2013) and from Damiano (Reference Damiano2015) show that most bouncers that correspond to our hashed region are identified as being in mode $(2,1)^{1}$ in the former and $(2,2)$ in the latter. Considering the difficulty to distinguish these cases experimentally, the agreement is excellent.

As mentioned above, the values of $\unicode[STIX]{x1D6FA}$ were swept by changing droplet radius in each simulation. However, we also computed certain cases with a different forcing frequency, for the same fluid in the bottom right region of figure 7, which produced a $(4,2)$ mode, as is seen in experiments (white squares in figure 10).

The other main discrepancy between theory and experiment that can be seen in this figure is the value of $\unicode[STIX]{x1D6E4}$ at which we observe the onset of chaotic bouncing is higher than experimentally observed values. Chaotic bouncing occurs for large $\unicode[STIX]{x1D6FA}$ and the difference can probably be explained by the importance of droplet deformation for larger drops which is not accounted for in our simulations.

For bouncers at $\unicode[STIX]{x1D6FA}=0.8$ , we trace the dependence of the phase of shaking corresponding to the impact and release of the droplet. We can thus compare the results to the experimental observations in Damiano (Reference Damiano2015) and the computations of Milewski et al. (Reference Milewski, Galeano-Rios, Nachbin and Bush2015). The background shadings in figure 11 correspond to the 95 % confidence interval of phase of impact and release found experimentally (A. P. Damiano, Personal communication, 2015). Each vertical traverse in this figure corresponds to a bouncer. At the bottom of the graph, every bouncer starts in flight and touches down as it reaches the first black curve. It then stays in contact until the next curve is reached (blue), at which moment it re-enters flight and repeats the same behaviour. As time increases, this figure is repeated periodically in the vertical direction. In the simulations; for $\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6E4}_{F}=0.48$ we see the transition from the $(1,1)$ mode to the $(2,2)$ mode and for $\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6E4}_{F}=0.71$ we see the $(2,2)$ mode to $(2,1)^{1}$ mode transition.

Figure 10. Regime diagram of bouncers. The background is colour coded according to the mode of bouncing observed in our simulations. The square bullets show experimentally observed bouncers, reported in Wind-Willansen et al. (Reference Wind-Willansen, Moláček, Harris and Bush2013). The colour coding of the squares is the same as that of the background, with the addition of white for the $(4,2)$ mode and pink for the $(4,3)$ mode, which were not found in this sweep of physical parameters with the simulations. The hashed area corresponds to modes that are to be strictly classified as $(2,2)$ ; however, the intermediate flight that separates the two contacts is rather subtle, and thus could be easily taken to be a $(2,1)^{1}$ . Walkers were found experimentally to the right of the red curve.

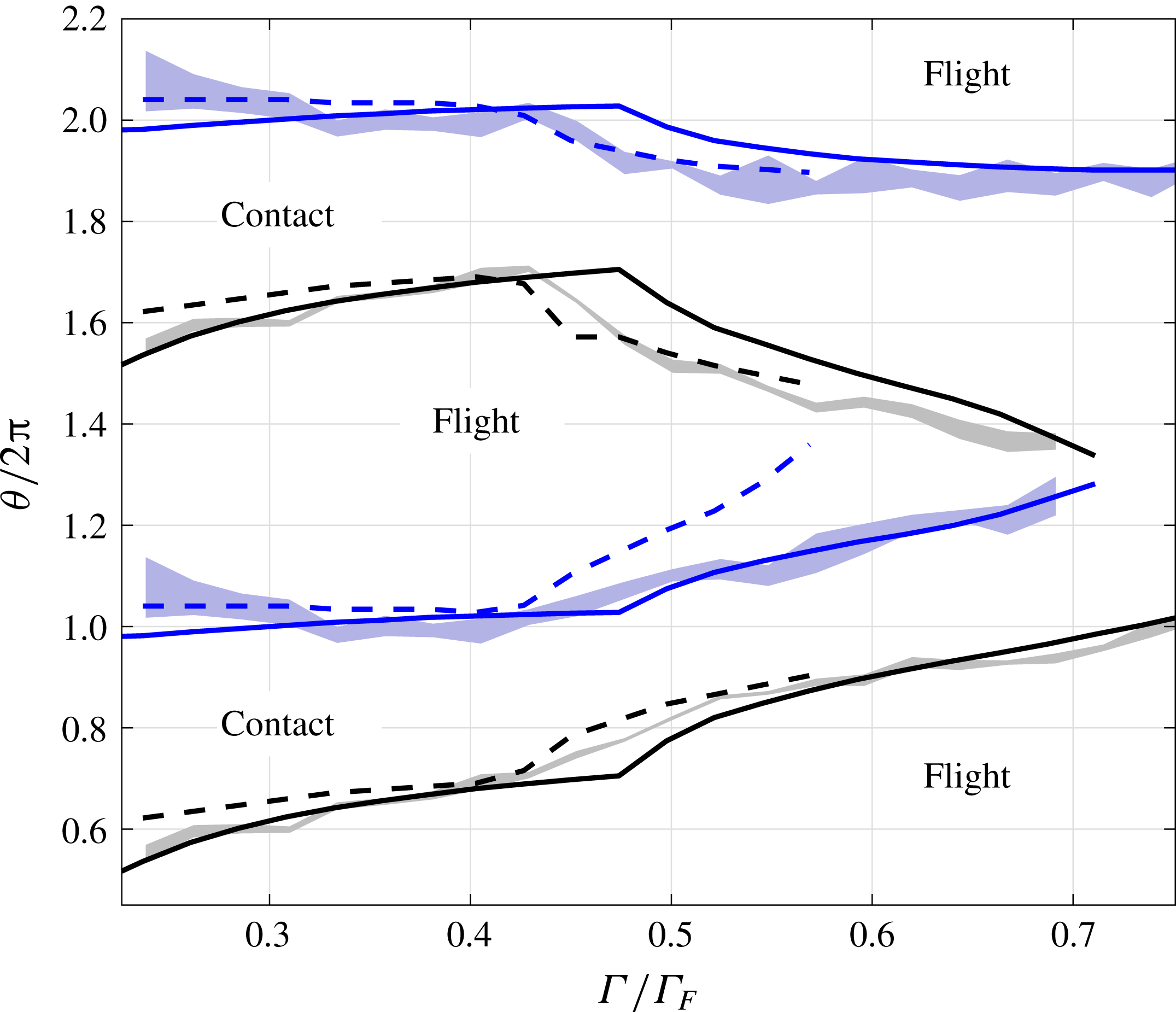
Figure 11. Experimental phases of impact (grey shading) and take off (blue shading), compared with predictions by the model presented in this work (solid lines). The vertical axis measures the phase of the shaker, with the convention that maximum height of the bath is attained at $\unicode[STIX]{x1D719}=0$ . The vertical extent of the shadings corresponds to the 95 % confidence interval about the value reported in Damiano (Reference Damiano2015). The dashed lines correspond to the predictions obtained using the (corrected) model presented in Milewski et al. (Reference Milewski, Galeano-Rios, Nachbin and Bush2015).

The experimental data in figure 11 correspond to a more recent experimental result which used more reliable techniques to determine contact. In particular, we notice that for $\unicode[STIX]{x1D6FA}=0.8$ and $0.5<\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6E4}_{F}<0.69$ , Damiano (Reference Damiano2015) reports a $(2,2)$ bouncing mode while Wind-Willansen et al. (Reference Wind-Willansen, Moláček, Harris and Bush2013) reports a $(2,1)^{1}$ mode. This supports our claim that in this regime it is hard to distinguish between the two, which was the base for our choice of the introduction of a hashed region in figure 10. Our simulations show better agreement with the more recent experimental results and better agreement with experiments than the logarithmic spring model.

Finally, we are able to compare our wave field predictions to the experimental observations reported in Damiano et al. (Reference Damiano, Brun, Harris, Galeano-Rios and Bush2016), where a surface Schlieren method was used to measure wave topography. Figure 12 shows a comparison of the radial profiles obtained by measurements and simulations. We note that the agreement is reasonable, especially considering the fact that there is no fit in phase. However, numerically computed waves tend to be larger in amplitude. This discrepancy between theory and experiment probably arises from our quasi-potential approximation and the simple form of the dissipation. In this approximation, all of the forcing due to droplet impact is deposited into wave modes, whereas it is probable that in reality non-wave-like vortical motions are also generated and rapidly dissipated, resulting in a smaller total wave response.

Figure 12. Comparison of the radial profiles of the experimental measurements (Damiano et al. Reference Damiano, Brun, Harris, Galeano-Rios and Bush2016) of wave topography (black) for a bouncer of $\unicode[STIX]{x1D6FA}=0.8$ and $\unicode[STIX]{x1D6E4}=3.25$ , i.e. just below the walking threshold, to the predictions of the model presented here (grey) for the same shaking. The vicinity of the origin is not shown, since in this region, the presence of the drop interferes with the measurements.